必备知识

重要性采样

基本概念

重要性采样

问题定义

• 函数$f(x)$，需从分布$p(x)$中采样，来计算期望值
• 但现在很难从$p(x)$中采样

方法

• 从另一个分布$q(x)$中采样(容易)，间接达到从$p(x)$中采样的效果(困难)

$$\begin{array}{ll}{E}_{x\sim p(x)}[f(x)]& =\int p(x)f(x)\mathrm{d}x\\ & =\int q(x)\cdot \frac{p(x)}{q(x)}f(x)\mathrm{d}x\\ & =E_{x\sim q(x)}[\frac{p(x)}{q(x)}f(x)]\end{array}$$

• 总结

$$E_{x\sim p}[f(x)]=E_{x\sim q}[\frac{p(x)}{q(x)}f(x)]=\frac{1}{N}\sum _i\frac{p(x_i)}{q(x_i)}f(x_i)$$

重要性权重

• $\frac{p(x)}{q(x)}$：用来修正采样的偏差，即两个分布之间的差异

IS是特殊MC采样

• 重要性采样也是一种特殊的MC采样
• 允许从简单分布采样，避免直接从困难分布采样的问题。

重要性采样的缺点

重要性采样缺点

缺点

• $q(x)$和$p(x)$差异较大时，方差很大，尽管期望相同。
  • $q$越接近$p$，方差越小；$q(x)$必须尽可能接近$p(x)$
  • 为什么分布接近方差小？见降低方差方法的公式推导 👍
• 当q和p差异大时，需通过足够多的采样，抵消差异对期望的影响
  • 如果采样次数不够多
    • $E_{x\sim p}[f(x)]$ 和 $E_{x\sim q}[\frac{p(x)}{q(x)}f(x)]$ 会有很大差异
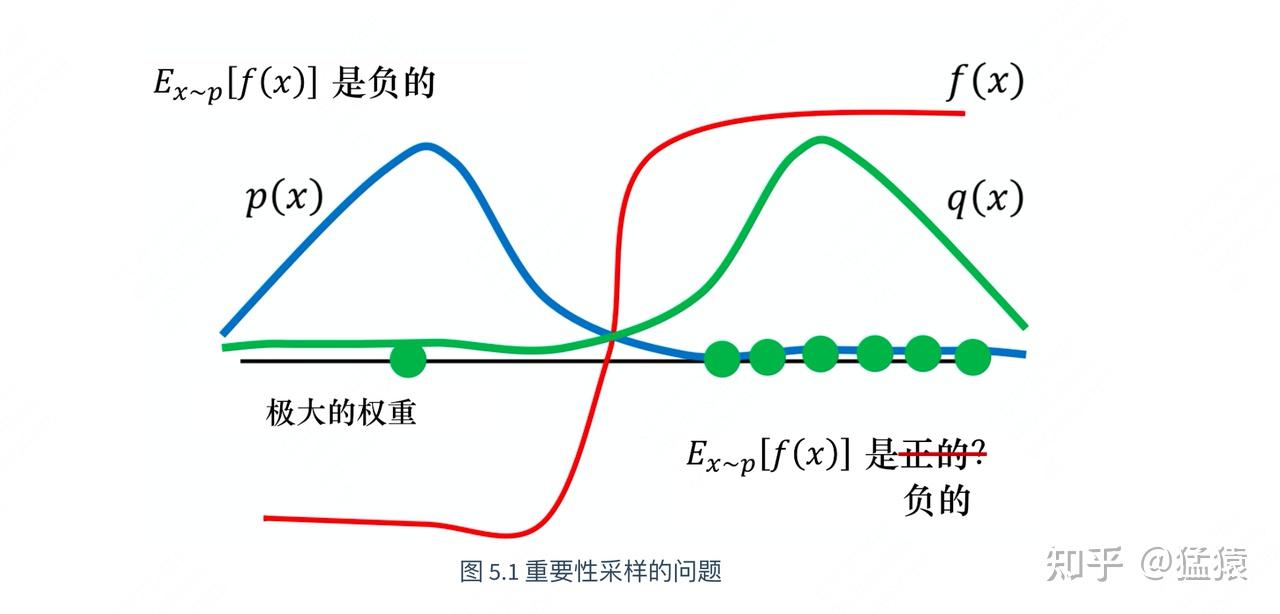
  • 比如下图
    • $E_{x\sim p}[f(x)]$本身是负的；
    • 但由于q和p差异大，大部分q都只能采样到正的，导致期望不对
  • 需足够多的采样，才能采到左边点，并给与其大权重，才能保证期望一致。
• 采样具有随机性，如果突然采样到方差大的样本，可能朝着错误方向更新。

解法

• 如果分布差异太大、采样数量又不够多怎么办？

  • KL约束(TRPO)：把${\pi }_{\theta }$和${\pi }_{{\theta }_{old}}$ 的相似性 作为$J({\pi }_{\theta })$的约束条件，信任区域。

  • CLIP(PPO)：把相似性约束条件，直接放回到目标函数$J({\pi }_{\theta })$中。

重要性采样在RL中的作用

重要性采样在RL中的作用

核心作用

• 可实现off-policy，从而降低RL采样成本，解决采样效率问题，提升训练效率。
  • on-policy：采样策略和学习策略相同
    • 即产出数据的策略和用这批数据做更新的策略是同1个。
• 更加谨慎地更新模型。

使用方法

• 从${\pi }_{old}$开始，用${\pi }_{old}$和环境交互，得到一批回合数据。
• 把这批回合数据 重复使用k次去更新模型( off-policy过程)
  • 第1次，喂给：${\pi }_{old}\to {\pi }_{{\theta }_1}$
  • 第2次，喂给：${\pi }_{{\theta }_1}\to {\pi }_{{\theta }_2}$
  • ...
  • 第k次，喂给：${\pi }_{{\theta }_{k-1}}\to {\pi }_{{\theta }_k}$
  • k次更新后：${\pi }_{old}={\pi }_{{\theta }_k}$

策略梯度发生变化

• 原始策略梯度

$$\mathrm{\nabla }J(\theta )=E_{(s_t,a_t)\sim {\pi }_{\theta }}[\underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{\theta }}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t\mid s_t)}}]$$

• 引入重要性采样后的梯度：$\tau \sim {\pi }_{{\theta }_{old}}$，训练数据是从旧策略采样出来的。

$$\mathrm{\nabla }J(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\underset{\mathrm{重}\mathrm{要}\mathrm{性}\mathrm{权}\mathrm{重}}{\underbrace{\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t\mid s_t)}}]$$

• 重要性权重

  $$r_t(\theta )=\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}=\frac{{\pi }_{\theta }(y_t\mid x,y_{<t})}{{\pi }_{{\theta }_{old}}(y_t\mid x,y_{<t})}$$$$r_{i,t}(\theta )=\frac{{\pi }_{\theta }(y_{i,t}\mid x,y_{i,<t})}{{\pi }_{{\theta }_{old}}(y_{i,t}\mid x,y_{i,<t})}$$

• 目标函数

$$\arg \underset{{\pi }_{\theta }}{max}J({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)]$$

重要性采样策略梯度推导

策略梯度推导过程

重要性采样策略梯度推导

从定义到期望形式

$$\begin{array}{ll}\mathrm{\nabla }J(\theta )& =\sum _{\tau }R(\tau )\cdot \mathrm{\nabla }{p}_{\theta }(\tau )\\ & =\sum _{\tau }R(\tau )\cdot p_{\theta }(\tau )\cdot \mathrm{\nabla }\log p_{\theta }(\tau )\\ & =E_{\tau \sim p_{\theta }(\tau )}[R(\tau )\cdot \mathrm{\nabla }\log p_{\theta }(\tau )]\end{array}$$

转换成优势策略梯度

$$\begin{array}{ll}\mathrm{\nabla }J(\theta )& =E_{\tau \sim p_{\theta }(\tau )}[R(\tau )\cdot \mathrm{\nabla }\log p_{\theta }(\tau )]\\ & =E_{(s_t,a_t)\sim {\pi }_{\theta }}[A(s_t,a_t)\cdot \mathrm{\nabla }\log {\pi }_{\theta }(a_t\mid s_t)]\end{array}$$

代入重要性采样

• 推导过程

$$\begin{array}{ll}\mathrm{\nabla }J(\theta )& =E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}\cdot A(s_t,a_t)\cdot \mathrm{\nabla }\log p_{\theta }(a_t\mid s_t)]\\ & =E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[A_{{\theta }_{old}}(s_t,a_t)\cdot \frac{p_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}\cdot \frac{1}{p_{\theta }(a_t\mid s_t)}\cdot \mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)]\\ & =E_{(s_t,a_t)\sim p_{{\theta }_{old}}}[A_{{\theta }_{old}}(s_t,a_t)\cdot \frac{1}{p_{{\theta }_{old}}(a_t\mid s_t)}\cdot \mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)]\\ & =E_{(s_t,a_t)\sim p_{{\theta }_{old}}}[A_{{\theta }_{old}}(s_t,a_t)\cdot \frac{\mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}]\\ & \approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}{A}_{{\theta }_{old}}(s_t,a_t)\cdot \frac{\mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}\end{array}$$

• 推导结果

$$\mathrm{\nabla }J(\theta )\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}{A}_{{\theta }_{old}}(s_t,a_t)\cdot \frac{\mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}$$

除以旧策略概率的作用 $\frac{\mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)}{p_{{\theta }_{old}}(a_t\mid s_t)}$

• $\frac{1}{p_{{\theta }_{old}}(a_t\mid s_t)}$：为了加权梯度$\mathrm{\nabla }{p}_{\theta }(a_t\mid s_t)$
  • 初期：模型不自信，预测概率较小，加权大，
  • 模型自信后：就不怎么加权了。
• 如果旧策略和当前策略梯度 冲突较大，会造成过度优化或 训不动。
• PPO-CLIP信任域 可解。

广义优势估计

GAE 相关笔记或文章

• TD(λ) 算法
• MC vs TD vs n步TD vs TD(λ) 核心公式对比
• GAE 广义优势估计
• 强化学习 —— 广义优势估计GAE

优势相关笔记

• A2C 优势算法
• A2C 优势及趋于0的理解
• Critic Loss 深入理解
• 策略梯度添加基线
• 策略梯度权重设计
• TD Error 估计优势 方差偏差问题
• 广义优势估计

TD(λ) 简介

TD(λ)

背景

• MC：无偏估计，低偏差、高方差。TD：有偏估计，高偏差、低方差。
• A2C引入优势函数来缓解了方差，但TD存在高偏差。需要平衡方差和偏差。

TD(λ)

• 一个n步回报$G_{t:t+n}$：采样n步，再做自举估计。

$$G_{t:t+n}=r_{t+1}+\gamma r_{t+2}+{\gamma }^2{r}_{t+3}+\cdots +{\gamma }^{n-1}{r}_{t+n}+{\gamma }^{n}V(s_{t+n})$$

• 对多个n步回报估计量进行加权平均，λ, 平衡了TD偏差和MC方差。
  • λ接近1，接近MC估计，偏差小、方差大。
  • λ接近0，接近单步TD，偏差大、方差小。
• $G_t^{\lambda }$ 定义

$$G_{t:T}^{\lambda }=(1-\lambda )\sum _{n=1}^{T-t-1}{\lambda }^{n-1}\cdot G_{t:t+n}+{\lambda }^{T-t-1}\cdot G_t$$$$\begin{array}{ll}{G}_t^{\lambda }& =(1-\lambda )\sum _{n=1}^{\mathrm{\infty }}{\lambda }^{n-1}\cdot G_{t:t+n}\end{array}$$

• V 函数更新，MC vs TD vs n步TD vs TD(λ) 核心公式对比

$$V(s_t)\leftarrow V(s_t)+\alpha \cdot (G_{t:t+n}-V(s_t))$$$$V(s_t)\leftarrow V(s_t)+\alpha \cdot (\underset{\lambda \mathrm{回}\mathrm{报}，\mathrm{多}\mathrm{个}n\mathrm{步}\mathrm{回}\mathrm{报},\mathrm{做}\mathrm{平}\mathrm{均}}{\underbrace{(1-\lambda )\sum _{n=1}^{\mathrm{\infty }}{\lambda }^{n-1}\cdot G_{t:t+n}}}-V(s_t))$$

GAE n步优势估计

GAE n步优势估计

1. 朴素 TD Error 定义

• 时刻$t$、步长为1、步长为2 的 TD Error定义
  • 注意：t时刻的即时奖励下标为$t$，这里$r_t$和 前面文章 $r_{t+1}$其实一样的

$${\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)$$$${\delta }_{t+1}=r_{t+1}+\gamma V(s_{t+2})-V(s_{t+1})$$

• 时刻$t$、步长为$l$ 的 TD Error 定义

$${\delta }_{t+l}=r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l})$$

2. n步优势估计 定义

• n步优势：使用n步回报来计算优势。
  • 参考 n步回报、λ回报

$$\begin{array}{ll}{A}_t^{(1)}=G_{t:t+1}-V(s_t)& =r_t+\gamma V(s_{t+1})-V(s_t)\\ A_t^{(2)}=G_{t:t+2}-V(s_t)& =r_t+\gamma r_{t+1}+{\gamma }^{2}V(s_{t+2})-V(s_t)\\ A_t^{(3)}=G_{t:t+3}-V(s_t)& =r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+{\gamma }^{3}V(s_{t+3})-V(s_t)\\ & ⋮& \\ A_t^{(n)}=G_{t:t+n}-V(s_t)& =r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots {\gamma }^{n}V(s_{t+n})-V(s_t)\\ & ⋮& \\ A_t^{(\mathrm{\infty })}=G_{t:t+\mathrm{\infty }}-V(s_t)& =r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots {\gamma }^T{r}_T+0+0+\cdots -V(s_t)\end{array}$$

• n步优势估计 定义公式
  • 步长 $n=\mathrm{\infty }$

$$A_t^{(\mathrm{\infty })}=G_{t:t+\mathrm{\infty }}-V(s_t)=\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot r_{t+l}-V(s_t)$$

3. n步优势估计 迭代计算公式

• 推导 $A_t^{(2)}$

$$\begin{array}{ll}{A}_t^{(2)}& =r_t+\gamma r_{t+1}+{\gamma }^{2}V(s_{t+2})-V(s_t)\\ & =(r_t+\gamma V(s_{t+1})-V(s_t))+(\gamma r_{t+1}+{\gamma }^{2}V(s_{t+2})-\gamma V(s_{t+1}))\\ & ={\delta }_t+\gamma \cdot {\delta }_{t+1}\end{array}$$

• n步优势估计 迭代计算公式

  • 步长2、3、4
  $$A_t^{(2)}={\delta }_t+\gamma \cdot {\delta }_{t+1}$$$$A_t^{(3)}={\delta }_t+\gamma \cdot {\delta }_{t+1}+{\gamma }^2\cdot {\delta }_{t+2}$$$$A_t^{(4)}={\delta }_t+\gamma \cdot {\delta }_{t+1}+{\gamma }^2\cdot {\delta }_{t+2}+{\gamma }^3\cdot {\delta }_{t+3}$$
  • 步长为$n、\mathrm{\infty }$

$$A_t^{(n)}=\sum _{l=0}^{n-1}{\gamma }^l\cdot {\delta }_{t+l}$$$$A_t^{(\mathrm{\infty })}=\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot {\delta }_{t+l}$$

4. 总结 n步优势 定义及计算公式

$$A_t^{(\mathrm{\infty })}=G_{t:t+\mathrm{\infty }}-V(s_t)=\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot r_{t+l}-V(s_t)=\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot {\delta }_{t+l}$$$$A_t^{(n)}=G_{t:t+n}-V(s_t)=\sum _{l=0}^{n-1}{\gamma }^l\cdot r_{t+l}-V(s_t)=\sum _{l=0}^{n-1}{\gamma }^l\cdot {\delta }_{t+l}$$

GAE 多个n步优势估计做加权平均

多个n步估计加权平均

• TD(λ) 多个n步回报加权平均
• GAE 多个n步优势估计加权平均

GAE 多个n步估计做加权

0. 背景

• 解决 TD Error 估计优势 方差偏差问题

1. GAE 定义公式

• 对多个$n$步优势估计量，进行加权平均(步数从1到n到无穷)，引入λ做方差、偏差平衡

$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=(1-\lambda )({\lambda }^0\cdot A_t^{(1)}+\lambda \cdot A_t^{(2)}+{\lambda }^2\cdot A_t^{(3)}+\cdots )$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=(1-\lambda )({\lambda }^0\cdot {\delta }_t+\lambda \cdot ({\delta }_t+\gamma {\delta }_{t+1})+{\lambda }^2\cdot ({\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2})+\cdots )$$

2. GAE 推导过程

$$\begin{array}{ll}{A}_t^{GAE(\gamma ,\lambda )}(s_t,a_t)& =(1-\lambda )({\lambda }^0\cdot A_t^{(1)}+\lambda \cdot A_t^{(2)}+{\lambda }^2\cdot A_t^{(3)}+\cdots )\\ & =(1-\lambda )({\delta }_t+\lambda \cdot ({\delta }_t+\gamma {\delta }_{t+1})+{\lambda }^2\cdot ({\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2})+\cdots )\\ & =(1-\lambda )({\delta }_t\cdot (1+\lambda +{\lambda }^2+\cdots )+\gamma {\delta }_{t+1}(\lambda +{\lambda }^2+\cdots )+{\gamma }^2{\delta }_{t+2}({\lambda }^2+{\lambda }^3+\cdots )+\cdots )\\ & =(1-\lambda )({\delta }_t\cdot \frac{1}{1-\lambda }+\gamma {\delta }_{t+1}\frac{\lambda }{1-\lambda }+{\gamma }^2{\delta }_{t+2}\frac{{\lambda }^2}{1-\lambda }+\cdots )\\ & ={\delta }_t+\gamma \lambda \cdot {\delta }_{t+1}+{\gamma }^2{\lambda }^2\cdot {\delta }_{t+2}+{\gamma }^3{\lambda }^3\cdot {\delta }_{t+3}+\cdots \\ & =\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}\\ & =\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))\end{array}$$

3. GAE 推导结果

$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{T-t-1}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))$$

4. GAE估计 vs 单个n步估计

• n步优势估计：采样n步，估计优势

$$A_t^{(n)}=\sum _{l=0}^{n-1}(\gamma {)}^l\cdot {\delta }_{t+l}$$

• GAE 优势估计：多个n步优势估计加权求平均$${\hat{A}}_t^{GAE}=\sum _{l=0}^{T-t-1}(\lambda \gamma {)}^l\cdot {\delta }_{t+l}$$

4. GAE 反向递推公式

• 从最后一个时间步开始，反向遍历，提高GAE计算效率

$$A_t^{GAE}(s_t,a_t)={\delta }_t+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})$$

5. λ=0时，退化单步TD估计

• 高偏差、低方差

$$A_t^{GAE(\gamma ,0)}(s_t,a_t)=(1-0)({\lambda }^0\cdot A_t^{(1)}+0\cdot A_t^{(2)}+0^2\cdot A_t^{(3)}+\cdots )$$$$A_t^{GAE(\gamma ,0)}(s_t,a_t)=A_t^{(1)}=G_{t:t+1}-V(s_t)=r_t+\gamma V(s_{t+1})-V(s_t)$$$$A_t^{GAE(\gamma ,0)}(s_t,a_t)=r_t+\gamma V(s_{t+1})-V(s_t)$$

6. λ=1时，退化完全MC采样估计

• 低偏差、高方差

$$\begin{array}{ll}{A}_t^{GAE(\gamma ,1)}(s_t,a_t)& =\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))\\ & =(r_t+\gamma V(s_{t+1})-V(s_t))+\gamma \cdot (r_{t+1}+\gamma V(s_{t+2})-V(s_{t+1}))+{\gamma }^2\cdot (r_{t+2}+\gamma V(s_{t+3})-V(s_{t+2}))+\cdots \\ & =r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots +{\gamma }^n{r}_{t+n}+\cdots -V(s_t)\\ & =\sum _{l=0}^{\mathrm{\infty }}{\gamma }^l\cdot r_{t+l}-V(s_t)\\ & =G_{t:t+\mathrm{\infty }}-V(s_t)=A_t^{(\mathrm{\infty })}(s_t,a_t)\end{array}$$$$A_t^{GAE(\gamma ,1)}(s_t,a_t)=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots +{\gamma }^n{r}_{t+n}+\cdots -V(s_t)$$

GAE中的奖励衰减(LLM)

奖励衰减

背景

• 在LLM任务中
  • 对最后token，仅$r_T=r_{EOS}\ne 0$
  • 对前面的token，环境奖励$r_t=0$，均为0。RM即时奖励

TD Error

• 对中间步$t<T$

  $${\delta }_t=0+V(s_{t+1})-V(s_t)=V(s_{t+1})-V(s_t)$$

• 对于最后一步$t=T$

$${\delta }_T=r_T+V(s_{T+1})-V(s_T)=r_T-V(s_T)$$

GAE 优势估计

• 推导过程

$$\begin{array}{ll}{\hat{A}}_t& =\sum _{l=0}^{T-t}(\lambda \gamma {)}^l\cdot {\delta }_{t+l}\\ & ={\delta }_t+(\lambda \gamma {)}^1{\delta }_{t+1}+(\lambda \gamma {)}^2{\delta }_{t+2}+\cdots +(\lambda \gamma {)}^{T-t-1}{\delta }_{T-1}+(\lambda \gamma {)}^{T-t}{\delta }_T\\ & =(\lambda \gamma {)}^{T-t}(r_T-V(s_T))+(V(s_{t+1})-V(s_t))+(\lambda \gamma {)}^1(V(s_{t+2})-V(s_{t+1}))+(\lambda \gamma {)}^2(V(s_{t+3})-V(s_{t+2}))+\cdots +(\lambda \gamma {)}^{T-t-1}(V(s_T)-V(s_{T-1}))\\ & =\underset{\mathrm{真}\mathrm{实}\mathrm{奖}\mathrm{励}\mathrm{信}\mathrm{号}}{\underbrace{(\lambda \gamma {)}^{T-t}{r}_T}}+\underset{\mathrm{来}\mathrm{自}\mathrm{价}\mathrm{值}\mathrm{函}\mathrm{数}\mathrm{估}\mathrm{计}\mathrm{的}\mathrm{信}\mathrm{号}}{\underbrace{(\text{一堆只包含}V(s)\text{的项})}}\end{array}$$

• 推导结果

$${\hat{A}}_t=\underset{\mathrm{真}\mathrm{实}\mathrm{奖}\mathrm{励}\mathrm{信}\mathrm{号}}{\underbrace{(\lambda \gamma {)}^{T-t}{r}_T}}+\underset{\mathrm{来}\mathrm{自}\mathrm{价}\mathrm{值}\mathrm{函}\mathrm{数}\mathrm{估}\mathrm{计}\mathrm{的}\mathrm{信}\mathrm{号}}{\underbrace{(\text{一堆只包含}V(s)\text{的项})}}$$

• 当$\lambda =1,\gamma =1$时，退回MC估计

$${\hat{A}}_t=r_T-V(s_t)$$

奖励衰减

• 从公式可看出，真实外部奖励信号 $r_T$ 传播回第t个token时，会乘以权重 $(\lambda \gamma {)}^{T-t}$、$(\lambda {)}^{T-t}$
• 当λ<1 且 T-t 很大时
  • 前面token收不到任何有效奖励信号。
  • 价值模型就无法学习到它们真正的贡献。

λ=1 vs λ<1

• λ<1
  • 在传统RL任务，每一步都有奖励，方差很大， 使用λ<1来降低方差，很有效
  • 在LLM任务中，奖励稀疏，$V_{target}$ 依赖自己自举
    • 如果一开始估计不准，就会导致错上加错，训练不稳定。
    • 带来的偏差危害(奖励信号衰减) 远远大于在降方差方面的好处。
• λ=1：
  • MC无偏估计，$V_{target}$ 只依赖环境奖励，价值模型学习变成简单的监督学习，非常稳定的梯度下降过程。

GAE 方差公式

GAE 方差公式

基础方差公式

$$\text{Var}[aX]=a^2\text{Var}(X)$$$$\text{Var}[X+Y]=\text{Var}[X]+\text{Var}[Y]+2\text{Cov}(X,Y)$$

GAE 方差推导

$${\hat{A}}_t^{\lambda }={\lambda }^0{\delta }_t+{\lambda }^1{\delta }_{t+1}+{\lambda }^2{\delta }_{t+2}+\cdots +{\lambda }^{T-t-1}{\delta }_{T-1}$$$$\begin{array}{ll}\text{Var}({\hat{A}}_t^{\lambda })& =\text{Var}[\sum _{l=0}^{T-t-1}{\lambda }^l\cdot {\delta }_{t+l}]\\ & =\sum _{l=0}^{T-t-1}{\lambda }^{2l}\cdot \text{Var}[{\delta }_{t+l}]+2\sum _{i=0}^{T-t-1}\sum _{j=i+1}^{T-t-1}{\lambda }^{i+j}\cdot \text{Cov}({\delta }_{t+i},{\delta }_{t+j})\end{array}$$

• 方差：由每一项自身方差和项与项之间的协方差共同决定。
• 减小λ会给这些项，更小的权重(尤其是后面的项)，从而降低总方差。

GAE 总结

GAE 总结

1. 时刻$t$、步长为$l$ 的 TD Error 定义

$${\delta }_{t+l}=r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l})$$

2. n步优势估计定义

$$A_t^{(n)}=G_{t:t+n}-V(s_t)=\sum _{l=0}^{n-1}{\gamma }^l\cdot r_{t+l}-V(s_t)=\sum _{l=0}^{n-1}{\gamma }^l\cdot {\delta }_{t+l}$$

3. GAE定义

• 对多个n步优势加权平均

$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=(1-\lambda )({\lambda }^0\cdot A_t^{(1)}+\lambda \cdot A_t^{(2)}+{\lambda }^2\cdot A_t^{(3)}+\cdots )$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=(1-\lambda )({\lambda }^0\cdot {\delta }_t+\lambda \cdot ({\delta }_t+\gamma {\delta }_{t+1})+{\lambda }^2\cdot ({\delta }_t+\gamma {\delta }_{t+1}+{\gamma }^2{\delta }_{t+2})+\cdots )$$

4. GAE 计算推导结果

$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))$$

5. GAE 反向递推公式

$$A_t^{GAE}(s_t,a_t)={\delta }_t+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})$$

6. λ=0/1

• λ=0时，GAE退化为单步TD估计

$$A_t^{GAE(\gamma ,0)}(s_t,a_t)=r_t+\gamma V(s_{t+1})-V(s_t)$$

• λ=1时，GAE退化完全MC采样

$$A_t^{GAE(\gamma ,1)}(s_t,a_t)=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots +{\gamma }^n{r}_{t+n}+\cdots -V(s_t)$$

• TD(λ)/TD(0)/TD(1)
  • λ越小，偏差越大、方差越小 (TD)
  • λ越大，偏差越小、方差越大 (MC)

GAE 作用

GAE 作用

优点/作用

• 平衡了单步优势估计中的MC-高方差和 TD-高偏差。

RL 优化目标

• 策略梯度权重多种形式

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重}}{\underbrace{{\mathrm{\Psi }}_t}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

• 引入GAE后的策略梯度

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{GAE\mathrm{作}\mathrm{权}\mathrm{重}}{\underbrace{A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

• 引入GAE + 重要性采样后的策略梯度

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{重}\mathrm{要}\mathrm{性}\mathrm{采}\mathrm{样}}{\underbrace{\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}}}\underset{GAE\mathrm{作}\mathrm{权}\mathrm{重}}{\underbrace{A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

• 优化目标

$$\arg \underset{{\pi }_{\theta }}{max}J({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)]$$

GAE 实现代码

@register_adv_est(AdvantageEstimator.GAE) 
def compute_gae_advantage_return(
    token_level_rewards: torch.Tensor,
    values: torch.Tensor,
    response_mask: torch.Tensor,
    gamma: torch.Tensor,
    lam: torch.Tensor,
):
    """Adapted from https://github.com/huggingface/trl/blob/main/trl/trainer/ppo_trainer.py

    Args:
        token_level_rewards: `(torch.Tensor)`
            shape is (bs, response_length)
        values: `(torch.Tensor)`
            shape is (bs, response_length)
        response_mask: `(torch.Tensor)`
            shape is (bs, response_length). [EOS] mask. The token after [EOS] have mask zero.
        gamma is `(float)`
            discounted factor used in RL
        lam: `(float)`
            lambda value when computing Generalized Advantage Estimation (https://arxiv.org/abs/1506.02438)

    Returns:
        advantages: `(torch.Tensor)`
            shape: (bs, response_length)
        Returns: `(torch.Tensor)`
            shape: (bs, response_length)

    """
    with torch.no_grad():
        nextvalues = 0
        lastgaelam = 0
        advantages_reversed = []
        gen_len = token_level_rewards.shape[-1]

        for t in reversed(range(gen_len)):
            delta = token_level_rewards[:, t] + gamma * nextvalues - values[:, t]
            lastgaelam_ = delta + gamma * lam * lastgaelam

            # skip values and TD-error on observation tokens
            nextvalues = values[:, t] * response_mask[:, t] + (1 - response_mask[:, t]) * nextvalues
            lastgaelam = lastgaelam_ * response_mask[:, t] + (1 - response_mask[:, t]) * lastgaelam

            advantages_reversed.append(lastgaelam)
        advantages = torch.stack(advantages_reversed[::-1], dim=1)

        returns = advantages + values
        advantages = verl_F.masked_whiten(advantages, response_mask)
    return advantages, returns

TRPO

Trust region policy optimization

ActorCritic 缺点

ActorCritic思想

Actor-Critic 核心思想

• 目标：找到${\theta }^{\ast }=\arg \underset{\theta }{max}J(\theta )$，沿${\mathrm{\nabla }}_{\theta }J(\theta )$方向迭代更新策略参数

$$J(\theta )=E_{s_0}[V^{{\pi }_{\theta }}(s_0)]=E_{{\pi }_{\theta }}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot r(s_t,a_t)]$$$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重},\mathrm{优}\mathrm{势}\mathrm{值}}{\underbrace{(r_t^n+\gamma V_{\pi }(s_{t+1}^n)-V_{\pi }(s_t^n))}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

• 参数更新

$$\theta \leftarrow \theta +\alpha \cdot \mathrm{\nabla }J(\theta )$$

Actor-Critic 缺点

Actor-Critic缺点

• 存在步长选择困难症：
  • 学习率太大：导致策略更新幅度太大，可能使策略性能下降，甚至崩溃。
  • 学习率太小：导致策略更新速度太慢，训练效率低下。
  • 虽然简单直观，但训练不稳定
  • 解法：KL 约束
• 每次梯度更新时，都需对${\pi }_{\theta }$做若干回合采样
  • 采样效率低，训练过程比较慢
  • 采样具有随机性，可能偶然采样到方差大的样本；如果直接信任，可能朝着错误方向更新
  • 解法：重要性采样
    • 降低采样成本，提升训练效率
    • 同时更加谨慎的更新模型
  • 重要性采样也需要两个分布差异不能太大
    • ${\pi }_{\theta }$和${\pi }_{old}$分布差异较大 且 采样轨迹数量不够大时，对$J(\theta )$的估计不准
    • 解法：KL约束
• TD Error 估计优势函数是有偏的
  • 具体详细见 TD Error 估计优势 方差偏差问题

TRPO 提出背景

• 解决步长选择困难症
  • 通过引入约束或限制，确保每次策略更新不会太大。
  • 避免策略崩溃，且保证策略能持续提升。
• 引入GAE平衡偏差和方差
• 使用重要性采样解决错误方向问题

信任区域

信任区域

信任区域作用理解

• 在策略空间中，策略的近似线性模型能够比较准确预测策略性能。

  • 在 信任区域，可以信任策略梯度，进行策略更新。
  • 离开信任区域，需重新评估策略性能，并调整更新方向。

• 解决重要性采样需要两个分布接近的缺点

  • ${\pi }_{\theta }$和${\pi }_{old}$ 分布差异较大 且 采样轨迹数量不够大时，对$J(\theta )$的估计不准。
  • 使用信任区域做限制。

• 信任区域是悟空给唐僧画的安全区

  • 在圈内，活动是绝对安全的。
  • 若要移动，需重新画圈圈，确保每一步走的安全、稳健。

信任区域定义 (KL约束条件)

• 其实是定义了一个KL约束，策略空间中的一个KL球，

• 保证新策略不会偏离旧策略太远，从而保证策略的单调提升

  $$\begin{array}{ll}& \underset{\theta }{max}{L}_{{\theta }_k}(\theta ),\\ & \mathrm{s}.\mathrm{t}.E_{s_t\sim {\rho }^{{\pi }_{{\theta }_k}}}[D_{KL}(\underset{\mathrm{旧}\mathrm{策}\mathrm{略}}{\underbrace{{\pi }_{{\theta }_k}(\cdot \mid s)}},\underset{\mathrm{新}\mathrm{策}\mathrm{略}}{\underbrace{{\pi }_{\theta }(\cdot \mid s)}})]\le \delta \end{array}$$

目标函数理解 $\underset{\theta }{max}{L}_{{\theta }_k}(\theta )$

• 通过调整策略参数$\theta$使目标最大化
  • $\theta$：正在优化的新策略，是需要寻找的参数
  • ${\theta }_k$：旧策略、已知的策略参数，第k次迭代
• L 目标函数，代理优势函数，衡量了新策略${\pi }_{\theta }$比旧策略${\pi }_{{\theta }_k}$有多好
  • L 通过重要性采样计算，利用旧策略 ${\pi }_{{\theta }_k}$采样的数据，来评估新策略 ${\pi }_{\theta }$的表现。
  • L > 0：说明新策略比旧策略好

约束条件理解

$$E_{s_t\sim {\rho }^{{\pi }_{{\theta }_k}}}[D_{KL}(\underset{\mathrm{旧}\mathrm{策}\mathrm{略}}{\underbrace{{\pi }_{{\theta }_k}(\cdot \mid s)}},\underset{\mathrm{新}\mathrm{策}\mathrm{略}}{\underbrace{{\pi }_{\theta }(\cdot \mid s)}})]\le \delta$$

• KL 散度 ：衡量两个概率分布的差异
  • $D_{KL}({\pi }_{{\theta }_k},{\pi }_{\theta })=0$：两个策略在状态s下完全一样
  • $D_{KL}({\pi }_{{\theta }_k},{\pi }_{\theta })$ 越大，说明新策略比旧策略变化越大。
• 所有状态$s_t$上的平均KL散度 需 $E_{s_t\sim {\rho }^{{\pi }_{{\theta }_k}}}\le \delta$，
  • 平均差异不能太大，限制在半径为$\delta$的小范围/信任区域内
    • 如0.01，信赖域大小
  • $s_t\sim {\rho }^{{\pi }_{{\theta }_k}}$：状态访问分布，访问各状态的概率是多少。
    • 根据旧策略访问这些状态的频率分布${\rho }^{{\pi }_{{\theta }_k}}$来加权，关注重要状态的策略变化

策略目标

TRPO 策略目标

$$J_{\mathrm{T}\mathrm{R}\mathrm{P}\mathrm{O}}({\pi }_{\theta })=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)],\mathrm{KL}({\pi }_{old},{\pi }_{\theta })\le \delta$$

TRPO 策略目标推导过程

核心目标

• 期望借助当前$\theta$找到一个更优${\theta }^{\prime }$，使得$J({\theta }^{\prime })\ge J(\theta )$

  • $\theta 、{\theta }^{\prime }$：旧策略、新策略。
  • ${\theta }_k、\theta$：旧策略、新策略。两种符号表示。

• 只要找到一个新策略，使$E_{s_t\sim v^{{\pi }_{{\theta }^{\prime }}}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[A^{{\pi }_{\theta }}(s_t,a_t)]\ge 0$，就能保证策略性能单调递增，推导过程见下文

$$\begin{array}{ll}J({\theta }^{\prime })-J(\theta )& =\frac{1}{1-\lambda }{E}_{s_t\sim {\rho }^{{\pi }_{{\theta }^{\prime }}}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[A^{{\pi }_{\theta }}(s_t,a_t)]\end{array}$$$$A^{{\pi }_{\theta }}(s_t,a_t)=r(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t)$$

难点

• 直接求解该式非常困难 $E_{s_t\sim {\rho }^{{\pi }_{{\theta }^{\prime }}}}$，${\pi }_{{\theta }^{\prime }}$ 是需要求解的新策略
  • 既用新策略收集样本数据，把所有可能的新策略都拿来收集数据
  • 然后判断哪个新策略符合上述条件，显然是不现实的。
• 解法：直接使用旧策略${\pi }_{\theta }$ 的状态分布
  • 新旧策略接近时，状态访问分布变化小，近似是合理的

$$E_{s_t\sim {\rho }^{{\pi }_{{\theta }^{\prime }}}}\to E_{s_t\sim {\rho }^{{\pi }_{\theta }}}$$

目标优化

• 直接采用旧策略${\pi }_{\theta }$的状态分布，忽略两个策略的状态访问分布

$$L_{\theta }({\theta }^{\prime })=J(\theta )+\frac{1}{1-\lambda }{E}_{s_t\sim {\rho }^{{\pi }_{\theta }}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[A^{{\pi }_{\theta }}(s_t,a_t)]$$

• 动作仍用新策略采样得到，用重要性采样做处理。
  • 这样就能基于旧策略${\pi }_{\theta }$ 采样出的数据，来估计并优化 新策略${\pi }_{{\theta }^{\prime }}$

$$L_{\theta }({\theta }^{\prime })=J(\theta )+E_{s_t\sim {\rho }^{{\pi }_{\theta }}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[\frac{{\pi }_{{\theta }^{\prime }}(a\mid s)}{{\pi }_{\theta }(a\mid s)}\cdot A^{{\pi }_{\theta }}(s_t,a_t)]$$

KL 约束 (上文信任域空间)

• 增加KL约束，保证新旧策略足够近

$$\begin{array}{ll}& \underset{{\theta }^{\prime }}{max}{L}_{\theta }({\theta }^{\prime }),\\ & \mathrm{s}.\mathrm{t}.E_{s_t\sim v^{{\pi }_{{\theta }_k}}}[D_{KL}({\pi }_{{\theta }_k}(\cdot \mid s),{\pi }_{\theta }(\cdot \mid s))]\le \delta \end{array}$$

• 信任区域：不等式约束定义了策略空间中的一个KL球。
• 在信任区域中
  • 学习策略和环境交互的状态分布，与上一轮策略最后采样的状态分布一致
  • 可以基于一步行动的重要性采样使当前学习策略稳定提升

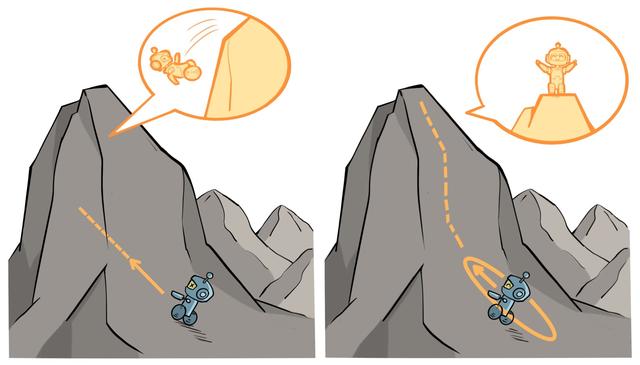
信任区域示意图：左侧无信任区域，梯度更新可能导致性能骤降；右侧有信任区域，每次梯度更新都能带来稳定提升。

目标推导过程

$J(\theta )$ 另一种形式

$$\begin{array}{ll}J(\theta )& =E_{s_0}[V^{{\pi }_{\theta }}(s_0)]\\ & =E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot V^{{\pi }_{\theta }}(s_t)-\sum _{t=1}^{\mathrm{\infty }}{\gamma }^t\cdot V^{{\pi }_{\theta }}(s_t)]\\ & =-E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot (\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t))]\end{array}$$

$J({\theta }^{\prime })-J(\theta )$推导过程

$$\begin{array}{ll}J({\theta }^{\prime })-J(\theta )& =E_{s_0}[V^{{\pi }_{{\theta }^{\prime }}}(s_0)]-E_{s_0}[V^{{\pi }_{\theta }}(s_0)]\\ & =E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot r(s_t,a_t)]+E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot (\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t))]\\ & =E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot (r(s_t,a_t)+\gamma V^{{\pi }_{\theta }}(s_{t+1})-V^{{\pi }_{\theta }}(s_t))]\\ & =E_{{\pi }_{{\theta }^{\prime }}}[\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot A^{{\pi }_{\theta }}(s_t,a_t)]\\ & =\sum _{t=0}^{\mathrm{\infty }}{\gamma }^t\cdot E_{s_t\sim v^{{\pi }_{{\theta }^{\prime }}}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[A^{{\pi }_{\theta }}(s_t,a_t)]\\ & =\frac{1}{1-\lambda }{E}_{s_t\sim v^{{\pi }_{{\theta }^{\prime }}}}{E}_{a\sim {\pi }_{{\theta }^{\prime }}(\cdot \mid s_t)}[A^{{\pi }_{\theta }}(s_t,a_t)]\end{array}$$

广义优势估计

GAE 笔记

GAE

• 对不同TD步数的优势估计进行指数加权平均，平衡方差和偏差

$${\delta }_{t+l}=r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l})$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))$$

def compute_advantage(gamma, lmbda, td_delta):
    td_delta = td_delta.detach().numpy()
    advantage_list = []
    advantage = 0.0
    for delta in td_delta[::-1]:
        advantage = gamma * lmbda * advantage + delta
        advantage_list.append(advantage)
    advantage_list.reverse()
    return torch.tensor(advantage_list, dtype=torch.float)

PPO

核心思想

PPO 核心思想

背景

• TRPO计算复杂， 每步更新运算量非常大。
• PPO基于TRPO思想，但实现更简单。能学的一样好、甚至更快。

PPO 核心思想

• 引入GAE

  • 解决单步优势的方差-偏差平衡问题。

• 引入重要性采样

  • 使用重要性权重 修正分布差异
  • 导致可使用off-Policy，提高采样效率，解决效率问题。

• 引入Clip或Penalty

  • 解决采样方差大& 重要性采样分布差异大+采样数量不足面临的问题

    • 把${\pi }_{\theta }$和${\pi }_{{\theta }_{old}}$的相似性 作为$J({\pi }_{\theta })$的约束条件。
      • TRPO：KL约束，做一个信任区域
      • PPO：把约束条件放回$J({\pi }_{\theta })$中做优化，CLIP 或 Penalty。

  • 使用Clip或Penalty 增强训练稳定性

PPO-Clip

Clip 核心思想

PPO-Clip

引入IS和GAE后的优化目标

$$\arg \underset{{\pi }_{\theta }}{max}J({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{GAE(\gamma ,\lambda )}(s_t,a_t)]$$

背景

• 为什么需要CLIP？

  • 考虑采样不足的情况下，${\pi }_{\theta }$和${\pi }_{{\theta }_{old}}$ 分布差异不能太大

  • 因此$\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}$是有上限和下限的，需保证$\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}$ 在信任域内。

  • 不能一味轻信 $A_{\varphi }^{GAE(\gamma ,\lambda )}(s_t,a_t)$， 来提升或降低 ${\pi }_{\theta }(a_t\mid s_t)$。

CLIP 核心思想

• 通过CLIP裁剪+MIN函数，限制策略更新幅度，来保证训练稳定性。
• 限制重要性权重在一个信任域内，超出信任域就裁切。
  • 约束新旧策略尽可能接近和相似，约束 ${\pi }_{\theta }$和${\pi }_{{\theta }_{old}}$的相似性，限制更新幅度不要太大，保证训练稳定性
  • 希望采样策略和学习策略的差距不要太大。

CLIP 信任域

• $[1-ϵ,1+ϵ]$

$$1-ϵ\le r_t(\theta )=\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\le 1+ϵ$$

优化目标

• 不做KL散度约束，直接把CLIP 信任域放到目标函数中

$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=E_{\tau \sim {\pi }_{{\theta }_{old}}}[min(r_t(\theta )\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t),\mathrm{clip}(r_t(\theta ),1-ϵ,1+ϵ)\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t))]$$$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=\sum _{s_t,a_t}min(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t),\mathrm{clip}(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)},1-ϵ,1+ϵ)\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t))$$

Clip 到底做了什么

CLIP 到底做了什么

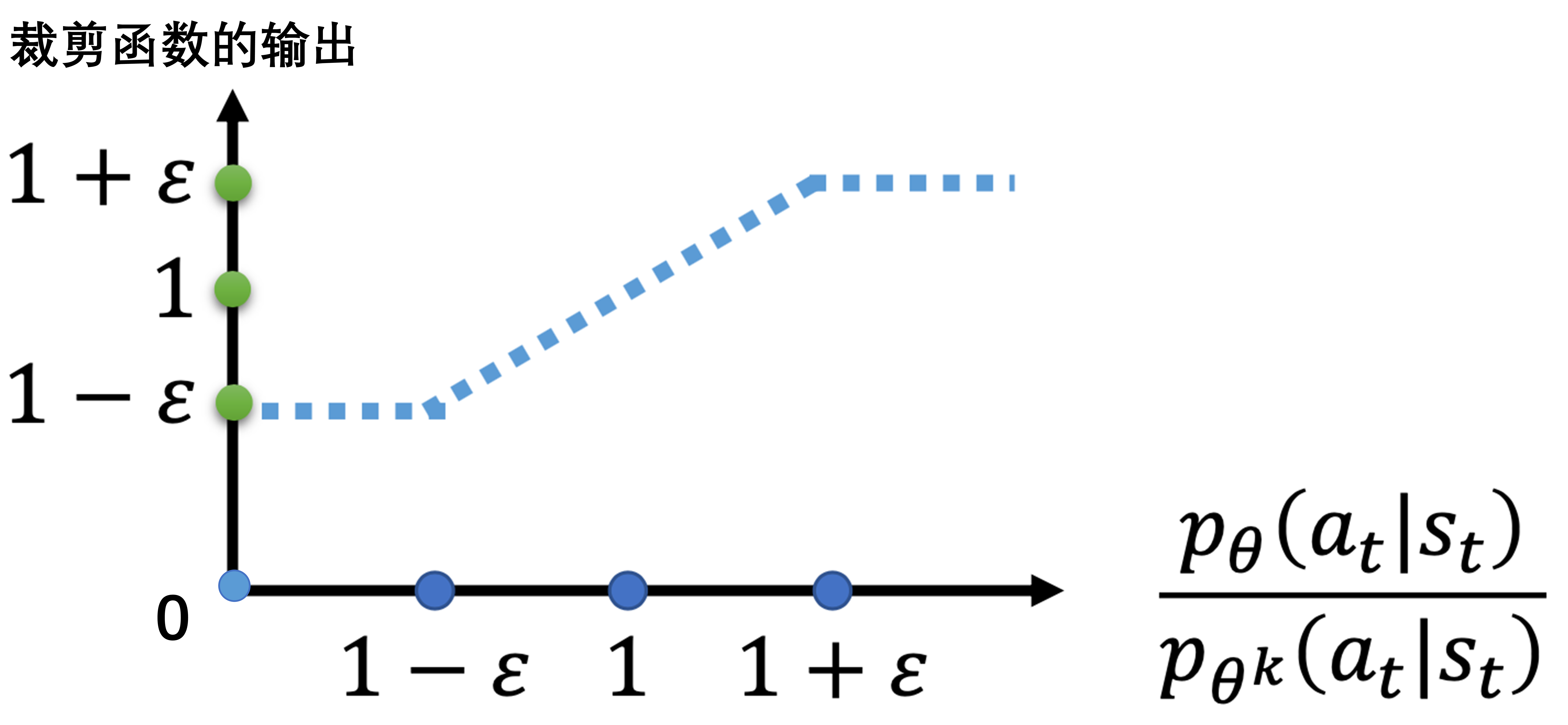
公式

• 无限制的策略梯度目标：$r_t(\theta )\cdot {\hat{A}}_t$
• 有限制的策略梯度目标：$\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)\cdot {\hat{A}}_t$，重要性权重裁剪到$[1-ϵ,1+ϵ]$

$$J^{\text{clip}}(\theta )=E_t[min(r_t(\theta )\cdot {\hat{A}}_t,\text{clip}(r_t(\theta ),1-ϵ,1+ϵ)\cdot {\hat{A}}_t)]$$

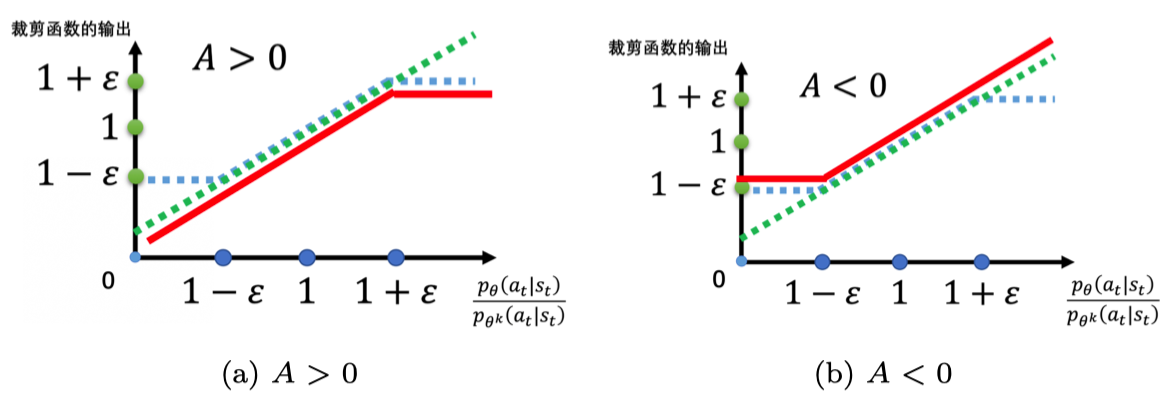
Case1：对于好动作 ${\hat{A}}_t>0$

• 目标：提高概率，即增大$r_t(\theta )$

• 当$r_t(\theta )\le 1+ϵ$时：一切正常

• 当$r_t(\theta )>1+ϵ$时：变成$(1+ϵ)\cdot {\hat{A}}_t$

  $$min(r_t(\theta )\cdot {\hat{A}}_t,(1+ϵ)\cdot {\hat{A}}_t)=(1+ϵ)\cdot {\hat{A}}_t$$

• $(1+ϵ)\cdot {\hat{A}}_t$，没有梯度

  • 是一个旧策略计算出的常数，和当前优化参数$\theta$ 无关

• 意味着IS差距大的token，该token梯度为0，无法进行梯度更新，该token被硬丢弃。

Case2：对于差动作 ${\hat{A}}_t<0$

• 目标：降低概率，即减小$r_t(\theta )$

• 当$r_t(\theta )<1-ϵ$时：变成$(1-ϵ)\cdot {\hat{A}}_t$

  $$min(r_t(\theta )\cdot {\hat{A}}_t,(1-ϵ)\cdot {\hat{A}}_t)=(1-ϵ)\cdot {\hat{A}}_t$$

• 同理，$(1-ϵ)\cdot {\hat{A}}_t$ 没有梯度，IS差异大的token，无法进行梯度更新，该token被硬丢弃。

Clip 改进工作

小心

• DAPO Clip-Higher
• CISPO Clip保留梯度
• DAPO Token-Level Loss

PPO-Penalty

PPO-Penalty

背景

• 直接把限制条件加入优化目标中，解决TRPO优化复杂的问题。
• 限制条件被称为KL penalty

KL Penalty

• KL散度， TRPO 信任区域 KL散度球
  • 约束行为上的距离，而不是参数上的距离，也因此无法使用L1L2范数等距离方法。

$$J_{PPO}^{{\pi }_{{\theta }_{old}}}(\theta )=J^{{\pi }_{{\theta }_{old}}}({\pi }_{\theta })-\beta \cdot {\mathrm{D}}_{\mathrm{KL}}({\pi }_{\theta },{\pi }_{{\theta }_{old}})$$

• 对KL散度设置阈值 $[{\mathrm{KL}}_{min},{\mathrm{KL}}_{max}]$
• 超参$\beta$的调整策略：自动调节、自适应KL散度
  • $\mathrm{KL}({\pi }_{\theta },{\pi }_{{\theta }_{old}})\ge {\mathrm{KL}}_{max}$
    • ${\pi }_{\theta }$ 新策略偏离旧策略太远 ，应该增大$\beta$，把分布拉回来
  • $\mathrm{KL}({\pi }_{\theta },{\pi }_{{\theta }_{old}})\le {\mathrm{KL}}_{min}$
    • 当前策略可能找到一条接近，只优化KL散度。
    • 让自己和旧策略相近，而不去优化优势相关的项
    • 应该减小$\beta$，降低KL散度对目标的影响。

优化目标

• 原始优化目标

$$\arg \underset{{\pi }_{\theta }}{max}J({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{GAE(\gamma ,\lambda )}(s_t,a_t)]$$

• 引入KL Penalty后的优化目标

$$\arg \underset{{\pi }_{\theta }}{max}{J}_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{K}\mathrm{L}}({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{old}}(s_t,a_t)-\beta \cdot \mathrm{K}\mathrm{L}({\pi }_{{\theta }_{old}}(\cdot \mid s_t),{\pi }_{\theta }(\cdot \mid s_t))]$$$$J_{PPO}^{KL}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t)]-\beta \cdot \mathrm{KL}({\pi }_{old},{\pi }_{\theta })$$

Actor

策略目标

PPO 策略目标

1. 普通优势策略目标

$$J_{\mathrm{优}\mathrm{势}}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)]$$

2. TRPO策略目标

$$J_{\mathrm{T}\mathrm{R}\mathrm{P}\mathrm{O}}({\pi }_{\theta })=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)],\mathrm{KL}({\pi }_{old},{\pi }_{\theta })\le \delta$$

3. PPO-CLIP 策略目标 ‼️

• 期望写法，Seq-Level-Loss

$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=E_{\tau \sim {\pi }_{{\theta }_{old}}}[min(r_t(\theta )\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t),\mathrm{clip}(r_t(\theta ),1-ϵ,1+ϵ)\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t))]$$$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=\sum _{s_t,a_t}min(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t),\mathrm{clip}(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)},1-ϵ,1+ϵ)\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t))$$

• 期望序列内平均写法，Seq-Level-Loss

$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=E_{q,o\sim {\pi }_{{\theta }_{old}}}\frac{1}{|o|}\sum _{t=1}^{|o|}min(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})}\cdot A_t,\mathrm{clip}(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})},1-ϵ,1+ϵ)\cdot A_t)$$$${\mathcal{L}}_{\text{ppo}}(\theta )=-\underset{\mathrm{样}\mathrm{本}\mathrm{间}\mathrm{平}\mathrm{均}}{\underbrace{\frac{1}{G}\sum _{i=1}^G}}\underset{\text{序列内平均}}{\underbrace{\frac{1}{|o_i|}\sum _{t=1}^{|o_t|}}}min(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})}\cdot {\hat{A}}_{i,t},\text{clip}(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})},1-ϵ,1+ϵ)\cdot {\hat{A}}_{i,t})$$

• 另有Token-Level Loss变体，2级平均，token-mean这是目前的主流。
  • 详细见 DAPO token-level loss, VAPO 解决长度不一问题

4. PPO-KLPenalty 策略目标

$$J_{PPO}^{KL}(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t)]-\beta \cdot \mathrm{KL}({\pi }_{old},{\pi }_{\theta })$$$$\arg \underset{{\pi }_{\theta }}{max}{J}_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{K}\mathrm{L}}({\pi }_{\theta })=E_{\tau \sim {\pi }_{old}}[\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{old}}(s_t,a_t)-\beta \cdot \mathrm{K}\mathrm{L}({\pi }_{{\theta }_{old}}(\cdot \mid s_t),{\pi }_{\theta }(\cdot \mid s_t))]$$

PPO Loss

Actor在PPO epoch中，使用同一批数据做迭代更新的。

PPO Loss

重要性采样/比率

• 为了稳定性，会对重要性采样做一个截断

$$r_t(\theta )=\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}$$$$r_t(\theta )=\text{clip}(r_t(\theta ),\text{min\_r},\text{max\_r})$$

• negative_approx_kl = log_prob - old_log_prob
• negative_approx_kl = torch.clamp(negative_approx_kl, min=-20.0, maxs=20.0)

PPO Loss

$${\text{L}}_{\mathrm{t}}^{\mathrm{P}\mathrm{P}\mathrm{O}-\mathrm{s}\mathrm{t}\mathrm{d}}=-min(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t),\mathrm{clip}(\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)},1-ϵ,1+ϵ)\cdot A_{\varphi }^{{\pi }_{{\theta }_{old}}}(s_t,a_t))$$$${\mathcal{L}}_{\text{ppo}}(\theta )=-\underset{\mathrm{样}\mathrm{本}\mathrm{间}\mathrm{平}\mathrm{均}}{\underbrace{\frac{1}{G}\sum _{i=1}^G}}\underset{\text{序列内平均}}{\underbrace{\frac{1}{|o_i|}\sum _{t=1}^{|o_t|}}}min(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})}\cdot {\hat{A}}_{i,t},\text{clip}(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})},1-ϵ,1+ϵ)\cdot {\hat{A}}_{i,t})$$

• DAPO token-level loss, VAPO 解决长度不一问题

Dual-Clip Loss

• 在优势$A_t<0$时，额外增加一个裁剪

$$L_t^{\text{Dual-Clip}}=\{\begin{array}{lll}& {\text{L}}_{\mathrm{t}}^{\mathrm{P}\mathrm{P}\mathrm{O}-\mathrm{s}\mathrm{t}\mathrm{d}}& A_t\ge 0\\ & min({\text{L}}_{\mathrm{t}}^{\mathrm{P}\mathrm{P}\mathrm{O}-\mathrm{s}\mathrm{t}\mathrm{d}},-c\cdot A_t)& A_t<0\end{array}$$

熵奖励

熵计算实现

熵奖励

背景

• 熵：信息量的期望，衡量不确定性的程度，熵越大，不确定性越大。
• RL容易陷入局部最优，停止探索。
• 为了鼓励策略探索，增加熵奖励。

计算方法

• 熵系数：entropy_coeff
• 熵loss：entropy_loss，response每个llm生成token熵的平均值。
  • entropy_loss = agg_loss(loss_mat=entropy, loss_mask=response_mask, loss_agg_mode=loss_agg_mode)
• 熵奖励：entropy_coeff * entropy_loss

$$L_{total}=L_{ppo}-{\beta }_H\cdot L_{entropy}$$

if calculate_entropy:
  	entropy = output["entropy"][:, -response_length - 1 : -1].contiguous()
    entropy_loss = agg_loss(loss_mat=entropy, loss_mask=response_mask, ...)
    entropy_coeff = meta_info["entropy_coeff"]
    # 核心：从PPO损失中减去熵损失（乘以一个系数）
    policy_loss = pg_loss - entropy_coeff * entropy_loss

KL 惩罚

KL3 散度：无偏且低方差

KL 惩罚

背景

• RLHF中通常有一个SFT后的${\pi }_{ref}$模型，具有一定能力。
• Reward Hacking问题：如果不对${\pi }_{\theta }$进行约束，可能会走捷径骗过RM，来获取高奖励。
• KL loss正则化手段，给策略上缰绳，允许追求高奖励、同时又防止跑偏太远。

计算公式

$$k{l}_{loss}=-\beta \cdot D_{KL}({\pi }_{\theta },{\pi }_{{\theta }_{ref}})$$$${D_{KL}}_t({\pi }_{\theta },{\pi }_{{\theta }_{ref}})=\frac{{\pi }_{ref}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-\log \frac{{\pi }_{ref}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-1$$

if self.config.use_kl_loss:
    ref_log_prob = data["ref_log_prob"]
    # compute kl loss
    kld = kl_penalty(logprob=log_prob, ref_logprob=ref_log_prob, kl_penalty=self.config.kl_loss_type)
    kl_loss = agg_loss(loss_mat=kld, loss_mask=response_mask, loss_agg_mode=self.config.loss_agg_mode)
		# 核心：将KL损失（乘以一个系数）加到总损失上
    policy_loss = policy_loss + kl_loss * self.config.kl_loss_coef

Policy总Loss

Policy 总Loss

总loss

Policy loss = PPO损失 - 熵奖励 + KL 惩罚

policy_loss = pg_loss - entropy_coeff * entropy_loss + kl_loss_coef * kl_loss

Policy Loss 代码

朴素PG loss

@register_policy_loss("vanilla")
def compute_policy_loss_vanilla(
    old_log_prob: torch.Tensor,
    log_prob: torch.Tensor,
    advantages: torch.Tensor,
    response_mask: torch.Tensor,
    loss_agg_mode: str = "token-mean",
    config: Optional[DictConfig | AlgoConfig] = None,
    rollout_log_probs: torch.Tensor | None = None,
) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor, torch.Tensor]:
    """
    Compute the clipped policy objective and related metrics for PPO.

    Adapted from
    https://github.com/huggingface/trl/blob/main/trl/trainer/ppo_trainer.py#L1122

    Args:
        old_log_prob (torch.Tensor):
            Log-probabilities of actions under the old policy, shape (batch_size, response_length).
        log_prob (torch.Tensor):
            Log-probabilities of actions under the current policy, shape (batch_size, response_length).
        advantages (torch.Tensor):
            Advantage estimates for each action, shape (batch_size, response_length).
        response_mask (torch.Tensor):
            Mask indicating which tokens to include in the loss, shape (batch_size, response_length).
        loss_agg_mode (str, optional):
            Aggregation mode for `agg_loss`. Defaults to "token-mean".
        config: `(verl.trainer.config.ActorConfig)`:
            config for the actor.
        rollout_log_probs: `(torch.Tensor)`:
            log probabilities of actions under the rollout policy, shape (batch_size, response_length).
    """

    assert config is not None
    assert not isinstance(config, AlgoConfig)
    clip_ratio = config.clip_ratio  # Clipping parameter ε for standard PPO. See https://arxiv.org/abs/1707.06347.
    clip_ratio_low = config.clip_ratio_low if config.clip_ratio_low is not None else clip_ratio
    clip_ratio_high = config.clip_ratio_high if config.clip_ratio_high is not None else clip_ratio
    clip_ratio_c = config.get(  # Lower bound of the ratio for dual-clip PPO. See https://arxiv.org/pdf/1912.09729.
        "clip_ratio_c", 3.0
    )

    cliprange = clip_ratio
    cliprange_low = clip_ratio_low
    cliprange_high = clip_ratio_high

    assert clip_ratio_c > 1.0, (
        "The lower bound of the clip_ratio_c for dual-clip PPO should be greater than 1.0,"
        + f" but get the value: {clip_ratio_c}."
    )

    negative_approx_kl = log_prob - old_log_prob 
    # Clamp negative_approx_kl for stability
    negative_approx_kl = torch.clamp(negative_approx_kl, min=-20.0, max=20.0) 
    ratio = torch.exp(negative_approx_kl)
    # 近似KL散度，作为监控指标
    ppo_kl = verl_F.masked_mean(-negative_approx_kl, response_mask)

    pg_losses1 = -advantages * ratio 
    if cliprange_low is None:
        cliprange_low = cliprange
    if cliprange_high is None:
        cliprange_high = cliprange
    pg_losses2 = -advantages * torch.clamp(
        ratio, 1 - cliprange_low, 1 + cliprange_high
    )  # - clip(ratio, 1-cliprange, 1+cliprange) * A
    clip_pg_losses1 = torch.maximum(
        pg_losses1, pg_losses2
    )  # max(-ratio * A, -clip(ratio, 1-cliprange, 1+cliprange) * A)
    
    # 被clip的比例
    pg_clipfrac = verl_F.masked_mean(torch.gt(pg_losses2, pg_losses1).float(), response_mask)

    pg_losses3 = -advantages * clip_ratio_c 
    clip_pg_losses2 = torch.min(pg_losses3, clip_pg_losses1) 
    # dual ppo clip 的比例
    pg_clipfrac_lower = verl_F.masked_mean(
        torch.gt(clip_pg_losses1, pg_losses3) * (advantages < 0).float(), response_mask
    )
		
    # dual ppo clip
    pg_losses = torch.where(advantages < 0, clip_pg_losses2, clip_pg_losses1)

    if config.tis_imp_ratio_cap > 0 and rollout_log_probs is not None:
        # Apply truncated importance sampling -> https://fengyao.notion.site/off-policy-rl
        tis_imp_ratio = torch.exp(old_log_prob - rollout_log_probs)
        tis_imp_ratio = torch.clamp(tis_imp_ratio, max=config.tis_imp_ratio_cap)
        pg_losses = pg_losses * tis_imp_ratio

    pg_loss = agg_loss(loss_mat=pg_losses, loss_mask=response_mask, loss_agg_mode=loss_agg_mode)

    return pg_loss, pg_clipfrac, ppo_kl, pg_clipfrac_lower

Policy Loss 增加 Entropy和KL loss

policy_loss = pg_loss

if calculate_entropy:
  entropy = output["entropy"][:, -response_length - 1 : -1].contiguous()
  if not forward_only:
      entropy_loss = agg_loss(loss_mat=entropy, loss_mask=response_mask, loss_agg_mode=loss_agg_mode)
      entropy_coeff = meta_info["entropy_coeff"]
      policy_loss = pg_loss - entropy_coeff * entropy_loss 
  else:
      ret_entropy = entropy

if forward_only:
  policy_loss = torch.tensor(1.0, device=device)
else:
  if self.config.use_kl_loss:
      ref_log_prob = data["ref_log_prob"]
      # compute kl loss
      kld = kl_penalty(logprob=log_prob, ref_logprob=ref_log_prob, kl_penalty=self.config.kl_loss_type)
      kl_loss = agg_loss(loss_mat=kld, loss_mask=response_mask, loss_agg_mode=self.config.loss_agg_mode)

      policy_loss = policy_loss + kl_loss * self.config.kl_loss_coef
      metrics["actor/kl_loss"] = kl_loss.detach().item()
      metrics["actor/kl_coef"] = self.config.kl_loss_coef

Reward

Reward Model 训练

Reward Model 训练

目标

• 给 (Prompt, Response) 打分，输出1个标量。

主流方法

• 偏好数据收集

  • 1个Prompt，输出多个Response，人类排序
  • 偏好数据：(prompt, chosen_response, rejected_response)

• 训练目标：好回复的分数比差回复的分数高

  $$RM(\text{prompt},\text{chosen\_response})>RM(\text{prompt},\text{rejected\_response})$$

• Pairwise Loss

  • ${\text{score}}_{chosen}-{\text{score}}_{reject}$：原始分数差；目标：最大化原始分数差
  • Sigmoid：模型认为 Chosen比Reject分数好的概率；目标：把概率推向1
  • $-\log$：交叉熵loss，对错误概率进行惩罚；目标：最小化惩罚

$$\text{loss}=-\log (\sigma (R(y_c\mid x)-R(y_r\mid x)))$$$$\text{loss}=-\log (\sigma ({\text{score}}_{chosen}-{\text{score}}_{reject}))$$

Reward Model 即时奖励

Reward

RM 打分

• 在NLP中，RM仅对整个Response打1个分，仅最后一个token才有奖励$r_T$，其余设为0。

  • 下文Critic目标之一：使最后一个token的回报 接近RM给的奖励 $r_T$$$V_{\varphi }(s_T)\leftrightarrow r_T$$

• 打分模型：训练过的Reward Model 或者 Rule-Based Func 或 LLM as Judge 等。

• 充当环境的作用，给每一步 即时奖励。

环境奖励信号

• 环境奖励$$r_t^{\text{env}}=\{\begin{array}{lll}0& 0\le t\le T-1& \mathrm{无}\mathrm{奖}\mathrm{励}\\ r_T& t=T& \text{最终奖励}\end{array}$$

最终奖励

• 最终每一步的奖励 = 环境奖励 -KL约束，KL 奖励约束见下文

$$r_t^{\text{total}}=r_t^{\text{env}}-\beta \cdot {D_{\text{KL}}}_t({\pi }_{\theta },{\pi }_{ref})=r_t^{\text{env}}-\beta \cdot \log \frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{ref}(o_t\mid q,o_{<t})}$$

• 由于KL约束非负，除$r_T$，其余token的奖励$r_t$ 要么是0、要么是负数。

奖励加入KL散度项

奖励加入KL散度

目的

• 确保 PolicyModel 不会偏离 ReferenceModel 太远。
• 如果偏离越大， 负的KL散度奖励，对策略的抑制也越大。

核心思想

• 对Policy和Reference模型的token预测分布，加入KL项。
• KL 负奖励

$${D_{\text{KL}}}_t({\pi }_{\theta },{\pi }_{ref})=\log \frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{ref}(o_t\mid q,o_{<t})}$$

最终奖励

• 最终奖励 = 环境奖励 - KL约束

$$r_t^{\text{total}}=r_t^{\text{env}}-\beta \cdot {D_{\text{KL}}}_t({\pi }_{\theta },{\pi }_{ref})=r_t^{\text{env}}-\beta \cdot \log \frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{ref}(o_t\mid q,o_{<t})}$$$$r_t=r_{\phi }(q,o_{\le t})-\beta \cdot \log \frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{ref}(o_t\mid q,o_{<t})}$$$$r(x,y)=r_{\varphi }(x,y)-\beta \cdot (\log {\pi }_{\theta }(y\mid x)-\log {\pi }_{ref}(y\mid x))$$

• 由于KL约束非负，除$r_T$，其余token的奖励$r_t$ 要么是0、要么是负数。

Critic

策略梯度相关loss

• 朴素PG策略梯度 Loss
• Actor-Critic 策略梯度及Loss
• PPO Critic Loss

Critic 目标

Critic 目标

Critic 核心目标

• 评估策略效果，Actor更新后，需新的Critic来衡量新策略的价值。

• 优化价值函数$V(s)$， 学习真实目标值

  • 让 $V(s)$预测 尽可能更接近真实的未来总回报。类比TD Error 定义
    • 预测当前策略，从状态$s$出发，未来总回报的期望值。
    • 是状态$s_t$的价值，不是即时奖励$r_t$。

• 但我们并不知上帝视角的真实目标值

  • 只能通过MC采样轨迹来估计，也就是Target Value，$V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$。

• 使最后一个token的回报 接近RM给的奖励 $r_T$

Critic 核心作用

• 通过不断“预测-验证-修正”的过程，Critic 的价值评估能力 越来越强。
• 从而能为 Actor 提供 更准确、更稳定的优势信号，最终引导 Actor 学会更好的策略

稀疏的监督信号

• 在LLM RL中，仅最后一个token 有RM给的奖励。
• 其他token 奖励都为0，其他token缺乏合适的奖励信号。
• 导致Critic Model非常难以训练 ‼️。

Critic 学习过程

Critic 学习过程

标准的监督学习

• 输入：状态$s$、 $s_t$
• 预测：$V_{\varphi }(s)$、$V_{\theta }(s_t)$、$V(s_t)$、$V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)$
  • Critic网络 在时间步$t$对状态$s_t$ 的价值预测。
  • $\varphi$是Critic 网络参数
• 目标：$V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t}}$、$V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$、$R_t$
  • 在时间步$t$，根据实际获得奖励、对真实回报的估计值。
  • 这是最核心内容，在下文详细介绍计算。
• Loss：预测值和目标值之间的差距，MSE loss。

算法流程

• 采样数据

  • Actor和环境交互，收集1个batch的轨迹数据

• 计算旧价值预测 $V_{old}(s_t)$

  • 使用当前Critic 对每一个状态$s_t$ 预测价值，得到$V_{old}(s_t)$，后面作为固定值

• 计算 TD Error

  • 对每个时间步t，计算TD Error
  $${\delta }_t=r_{t+1}+\gamma V_{\pi }(s_{t+1})-V_{\pi }(s_t)$$
  • $r_{t+1}$ 是环境给的即时奖励，可通过Reward Model 或 Reward Func给出

• 计算 GAE 优势估计

  • GAE 公式

    $$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$

  • 从最后一个时间步开始，反向遍历，提高GAE计算效率

    $$A_t^{GAE}(s_t,a_t)={\delta }_t+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})$$

• 计算 Critic 目标值：利用GAE优势 + 旧价值预测 $V_{old}(s_t)$

$$V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}=A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)+V_{old}(s_t)$$

• 计算 Critic Loss （见下文详细说明）

  • 在PPO多个优化子周期(epoch)里，对batch中每个数据点 $(s_t,V_{old}(s_t))$

    • 把$s_t$输入到正在更新的Critic网络，得到新预测值 $V_{\varphi }(s_t)$

    • 利用Critic 目标值 和 Critic 最新预测值，计算 MSE Loss

      $$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(V_{\varphi }(s_t)-V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}{)}^2$$

    • 根据Critic Loss调整Critic网络，争取下次预测的更准。

Critic Loss

Critic Loss

Loss函数

• 实际训练中，从收集到的数据，取batch，计算batch上所有时间步的平均loss

$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}-V_{\theta }(s_t){)}^2$$$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=\frac{1}{N}\sum _{t=1}^N(V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}-V_{\varphi }(s_t){)}^2$$

• Loss 类比于 TD Error

$${\delta }_t=\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{r_{t+1}+\gamma V(s_{t+1})}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V(s_t)}}$$$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)}}{)}^2$$$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{R_t}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\theta }(s_t)}}{)}^2$$

Critic目标值/真实回报目标值计算 $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$、$R_t$

• 最核心部分， $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$ 计算方法直接影响Critic的学习效率和稳定性

• 优势函数计算

  • 朴素优势函数：优势函数趋于0的理解

    • 要估计Q和V2个网络，复杂。
    $$A_{\pi }(s_t,a_t)=Q_{\pi }(s_t,a_t)-V_{\pi }(s_t)$$

  • TD Error 近似优势估计

    • 仅V一个网络，但偏差大，TD Error 估计优势 方差偏差问题`
    $$A_{\pi }(s_t,a_t)={\delta }_t=\underset{TD\mathrm{误}\mathrm{差}}{\underbrace{r_{t+1}+\gamma V_{\pi }(s_{t+1})-V_{\pi }(s_t)}}$$

  • GAE平衡 TD偏差和MC方差

    • 综合多个n步优势估计$$A_t^{GAE}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$

• $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$ 计算 ‼️

  • 目标回报Q值 = 优势值 + V值

    $$A_{\pi }(s_t,a_t)=Q_{\pi }(s_t,a_t)-V_{\pi }(s_t)\to Q_{\pi }(s_t,a_t)=A_{\pi }(s_t,a_t)+V_{\pi }(s_t)$$

  • Critic 学习目标是真实回报，可以看作是$Q_t$的一个估计，得到

    $$V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}=A_t^{GAE}(s_t,a_t)+V_{old}(s_t)$$

  • 请注意

    • $V_{old}(s_t)$：用当时旧的Critic网络预测并记录下来旧的、固定的值，在GAE之前

      • 当做常数，不参与梯度计算。

    • $A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)$：$V_{old}$值计算出来的。

  • $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$理解

    • 基于旧价值函数的估计 + 这个估计的修正量(优势值) = 得到 更精确的回报估计。

Critic Loss 深入理解

Critic Loss TD Error 类比

TD Error

$${\delta }_t=\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{r_{t+1}+\gamma V(s_{t+1})}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V(s_t)}}$$

Critic Loss

$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)}}{)}^2$$

TD Error 类比

$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=(\underset{\mathrm{目}\mathrm{标}\mathrm{值}}{\underbrace{R_t}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\theta }(s_t)}}{)}^2$$

• $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$、$R_t$ ：类比 TD 目标值

• $V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)$、$V_{\varphi }(s_t)$：类比TD Error中的需要优化的价值函数，当前网络的预测值

• Loss 类比 TD Error

Critic Loss 再深入理解

GAE 优势 推导

• 反向递推公式

$$\begin{array}{ll}{A}_t^{GAE}(s_t,a_t)& ={\delta }_t+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})\\ & =r_{t+1}+\gamma V_{old}(s_{t+1})-V_{old}(s_t)+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})\end{array}$$

• 推导结果

$$A_t^{GAE}(s_t,a_t)=r_{t+1}+\gamma V_{old}(s_{t+1})-V_{old}(s_t)+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})$$

目标回报值 推导

• R = A + V

$$\begin{array}{ll}{R}_t=V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}& =A_t^{GAE}(s_t,a_t)+V_{old}(s_t)\\ & =r_{t+1}+\gamma V_{old}(s_{t+1})-V_{old}(s_t)+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})+V_{old}(s_t)\\ & =r_{t+1}+\gamma V_{old}(s_{t+1})+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})\end{array}$$

• 推导结果
  • 其实在朴素单步TD目标值基础上加了一个GAE估计。

$$R_t=V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}=r_{t+1}+\gamma V_{old}(s_{t+1})+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})$$

代入计算Loss

$$\begin{array}{ll}{L}_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}& =(R_t-V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t){)}^2\\ & =(\underset{TD\mathrm{目}\mathrm{标}，\mathrm{增}\mathrm{加}GAE}{\underbrace{r_{t+1}+\gamma V_{old}(s_{t+1})+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})}}-\underset{\mathrm{最}\mathrm{新}\mathrm{网}\mathrm{络}\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)}}{)}^2\end{array}$$$$\begin{array}{ll}{L}_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}& =(\underset{TD\mathrm{目}\mathrm{标}，\mathrm{增}\mathrm{加}GAE}{\underbrace{r_{t+1}+\gamma V_{old}(s_{t+1})+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})}}-\underset{\mathrm{最}\mathrm{新}\mathrm{网}\mathrm{络}\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)}}{)}^2\end{array}$$

• 和 A2C 中优势趋于0的理解是完全一致的。

Critic Value Clip

Value Function Clip

背景

• 稳定训练技巧，防止Critic网络更新过大，对新价值预测做裁剪。

价值更新裁剪

• $ϵ$是超参 例如(0.2)，和Actor Loss 裁剪范围通常相同。$$V_{\mathrm{clipped}}(s_t)=\mathrm{clip}(V_{\theta }(s_t),V_{\mathrm{old}}(s_t)-ϵ,V_{\mathrm{old}}(s_t)+ϵ)$$

计算未裁剪和裁剪后的2个loss

• 未裁剪

  $$L_{\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}}=(V_{new}(s_t)-V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}{)}^2$$

• 裁剪后

$$L_{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}}=(V_{\mathrm{clipped}}(s_t)-V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}{)}^2$$

最终Critic Loss 取较大者

$$L_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}=max(L_{\mathrm{u}\mathrm{n}\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}},L_{\mathrm{c}\mathrm{l}\mathrm{i}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{d}})$$

具体稳定训练过程思考

• 建立信任区域

  • 围绕旧值$V_{\mathrm{old}}(s_t)$建立信任区域，相信旧价值预测大体上是正确的。

    $$[V_{\mathrm{old}}(s_t)-ϵ,V_{\mathrm{old}}(s_t)+ϵ]$$

  • 确保新价值预测$V_{new}(s_t)$不会离旧价值预测$V_{\mathrm{old}}(s_t)$ 太远。

  • 预测价值本该朝向目标回报靠近，但若预测价值超出信任区域，则应该Clip。

    $$V_{new}(s_t)\to R_t$$

• 防止因目标值不准而过度更新

  • $V_{\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}\mathrm{t},\mathrm{t}}$ 是由GAE计算出来的，是估计值，存在方差。

• 保持 Actor和Critic 更新步调一致

  • PPO核心是限制策略更新幅度，为Actor提供指导信号的Critic也应该限制更新幅度。
  • 防止Critic剧烈变化导致下一轮优势估计出现波动，导致Actor训练不稳定。

重要性采样

PPO 重要性采样

策略梯度

• 交互策略${\pi }_{{\theta }_{old}}$：与环境交互，采集大量数据来训练${\pi }_{\theta }$
• 学习策略${\pi }_{\theta }$：要训练学习的网络
• ${\pi }_{\theta }$更新多次后，再去更新${\pi }_{{\theta }_{old}}$

$$\mathrm{\nabla }J(\theta )=E_{\tau \sim p_{{\theta }_{old}}(\tau )}[\frac{p_{\theta }(\tau )}{p_{{\theta }_{old}}(\tau )}R(\tau )\mathrm{\nabla }\log p_{\theta }(\tau )]$$

优势策略梯度

• 优势作权重

$$\mathrm{\nabla }J(\theta )=E_{(s_t,a_t)\sim {\pi }_{\theta }}[\underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{\theta }}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log {\pi }_{\theta }(a_t\mid s_t)}}]$$

• 引入重要性采样

$$\mathrm{\nabla }J(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\underset{\mathrm{重}\mathrm{要}\mathrm{性}\mathrm{权}\mathrm{重}}{\underbrace{\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{\theta }}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log {\pi }_{\theta }(a_t\mid s_t)}}]$$

• 优势应是演员和环境交互 计算出来的

$$\mathrm{\nabla }J(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\underset{\mathrm{重}\mathrm{要}\mathrm{性}\mathrm{权}\mathrm{重}}{\underbrace{\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t\mid s_t)}}]$$

目标函数

$$J(\theta )=E_{(s_t,a_t)\sim {\pi }_{{\theta }_{old}}}[\underset{\mathrm{重}\mathrm{要}\mathrm{性}\mathrm{权}\mathrm{重}}{\underbrace{\frac{{\pi }_{\theta }(a_t\mid s_t)}{{\pi }_{{\theta }_{old}}(a_t\mid s_t)}}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{权}\mathrm{重}}{\underbrace{A^{{\pi }_{{\theta }_{old}}}(s_t,a_t)}}]$$

优点

• 可通过重要性采样把同策略换成异策略

GAE

GAE 笔记

GAE

• 对不同步数的TD优势估计进行指数加权平均，平衡方差和偏差

$${\delta }_{t+l}=r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l})$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot {\delta }_{t+l}$$$$A_t^{GAE(\gamma ,\lambda )}(s_t,a_t)=\sum _{l=0}^{\mathrm{\infty }}(\gamma \lambda {)}^l\cdot (r_{t+l}+\gamma V(s_{t+l+1})-V(s_{t+l}))$$

算法流程

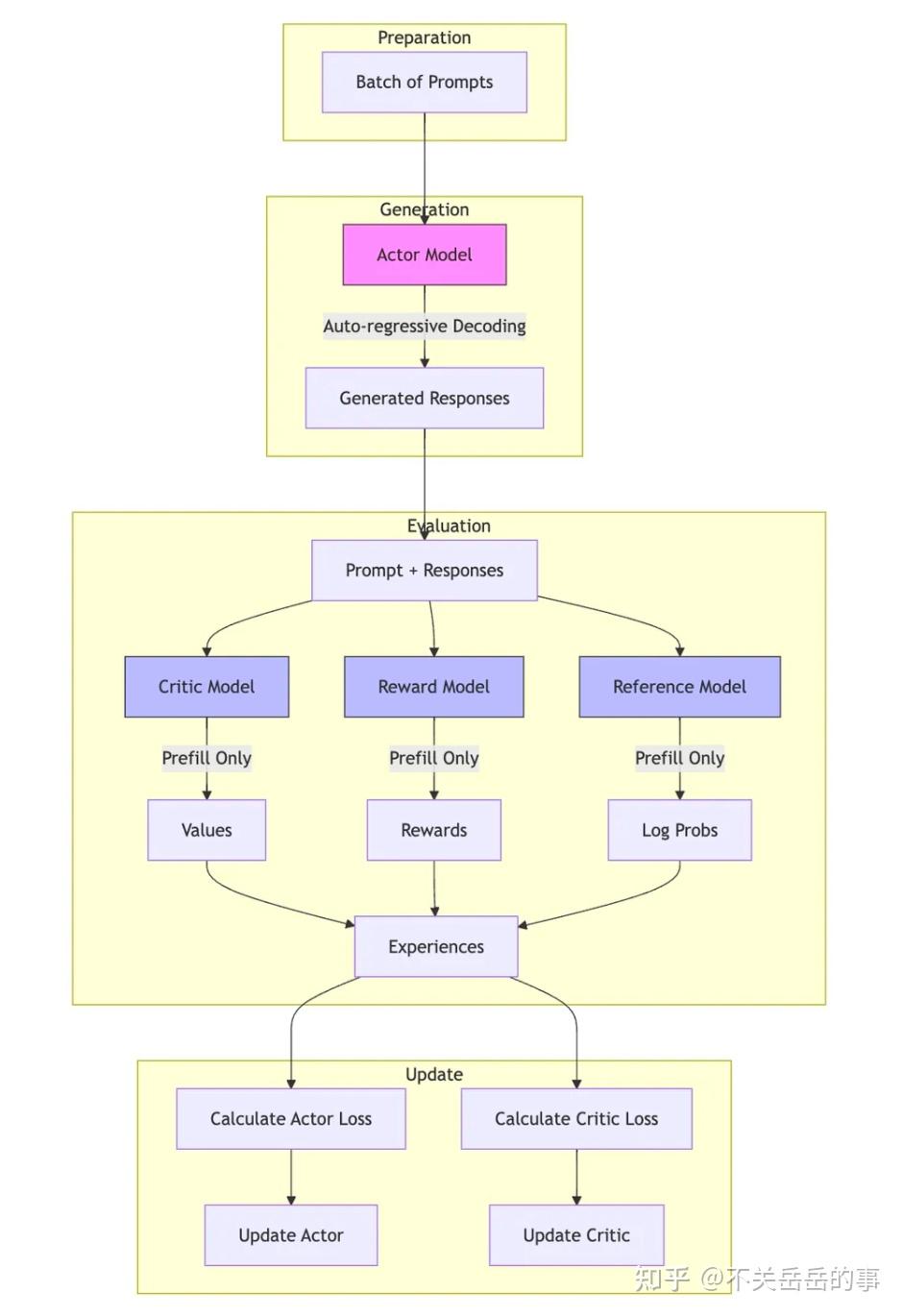
算法流程

PPO算法流程

• 初始策略参数${\theta }^0$
• 每次迭代
  • 用旧策略${\theta }^k$ 和环境交互，采样大量$(s,a)$对
  • 根据${\theta }^k$交互结果，估计$A^{{\pi }_{{\theta }^k}}(s_t,a_t)$
  • 采样到这组数据后，最大化目标函数
  • 可以让$\theta$更新很多次

$$J_{PPO}^{{\theta }^k}(\theta )=J^{{\theta }^k}(\theta )-\beta \cdot \mathrm{KL}(\theta ,{\theta }^k)$$

PPO 调参踩坑经验

PPO 主要注意点

主要坑点

• Critic初始化
  • 要用预训练权重， 随机初始化基本gg
• KL散度监控
  • 超过0.02就要降学习率，不然策略会崩
• 内存管理
  • 内存需求爆炸，双网络+梯度存储
• 超参数敏感
  • 学习率、裁切范围，都很敏感

部分参数

• learning_rate：3e-4直接爆炸，降到1.5e-5才稳定
• batch_size：小于128，训练震荡严重
• clip_range：跳到0.4后，策略变化太激进

来自 知乎 PPO vs GRPO

# 稳定的PPO配置（13B模型）
ppo_config = {
    "learning_rate": 1.5e-5,  # 别用太大，容易崩
    "clip_range": 0.2,        # 经典值，基本不用改
    "batch_size": 256,        # 越大越稳定
    "gae_lambda": 0.95,       # GAE参数
    "value_loss_coef": 0.5,   # 价值损失权重
    "entropy_coef": 0.01,     # 探索系数
    "max_grad_norm": 1.0,     # 梯度剪切
    "n_epochs": 4,            # 数据重用次数
}

缺点不足

PPO不足

GAE带来的计算开销大、训练不稳定

• GAE 主要依赖于单步时序误差

$$\delta =r_t+\gamma V(s_{t+1})-V(s_t)$$

• 计算TDError之前，需为每个token计算奖励和价值
  • 每个token的价值：需由独立的Critic模型计算得到
  • Critic通常和策略模型同架构和大小，Critic计算开销非常大，且训练不稳定导致 无法提供准确的价值信号

DPO

参考文章

• 人人都能看懂的DPO数学原理
• dpo 的局限性
• 简单例子说明 DPO 为什么可能表现不好
• DPO 是如何简化 RLHF 的

标准RLHF目标

标准RLHF目标

标准RLHF目标-tradeoff

• 最大化奖励：${\pi }_{\theta }$ 生成的回答$y$，从奖励模型尽可能获得高分
• 不要偏离太远：约束策略${\pi }_{\theta }$和参考策略${\pi }_{ref}$ 保持一定相似性。${\pi }_{sft}$

$$\underset{{\pi }_{\theta }}{max}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[r_{\varphi }(x,y)-\beta \cdot D_{KL}({\pi }_{\theta }(y\mid x),{\pi }_{ref}(y\mid x))]$$

• 奖励函数

$$r(x,y)=r_{\varphi }(x,y)-\beta \cdot (\log {\pi }_{\theta }(y\mid x)-\log {\pi }_{ref}(y\mid x))$$

标准RLHF训练流程

• 先训rewad model

  $$\underset{r_{\varphi }}{max}{E}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (r_{\varphi }(x,y_w)-r_{\varphi }(x,y_l))]$$

• 再通过PPO训Actor Model

  $$\underset{{\pi }_{\theta }}{max}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[r_{\varphi }(x,y)-\beta \cdot D_{KL}({\pi }_{\theta }(y\mid x),{\pi }_{ref}(y\mid x))]$$

PPO缺点 & DPO动机

PPO缺点 & DPO动机

PPO 缺点

• 计算复杂、成本高
  • Actor、CriticModel(估计价值,降低梯度估计中的方差)、RewardModel(奖励信号)、SFTModel (KL散度)
• 训练不稳定
  • 奖励稀疏、梯度更新不稳定、收敛困难、参数敏感等
• Reward Hacking
  • RM从有限的人类偏好数据中学习的，不可避免存在缺陷和偏差。
  • 策略在优化过程中，发现并利用RM的漏洞，获得高分 但实际不符合人类预期的输出。
  • 把复杂抽象的人类价值观，压缩成简单的标量信号，是很困难的。

DPO 动机

• 把带有KL约束最大化奖励目标，等价替换成简单的直接在偏好数据上进行优化的分类问题。
• 把对齐问题重定义为最大似然估计问题，简单二元交叉熵loss，直接对偏好Pair数据优化。
• 完全绕过 显示奖励模型训练和复杂RL训练。这两个恰好是RLHF中最贵和不稳定的环节。
• 并非性能上超越RLHF，而是工程上的成功。更稳定、更轻量、更容易实现。

理论基础

显示最优解

显示最优解推导过程

PPO式子理论存在显示最优解

• 理论最优解：通过完美奖励函数计算出完美策略模型，不需要迭代式的强化学习。
• 最优策略、参考策略、奖励函数之间的确定性关系。

$${\pi }_r^{\ast }(y\mid x)=\frac{1}{Z(x)}\cdot {\pi }_{ref}(y\mid x)\cdot \exp (\frac{1}{\beta }r(x,y))$$

• $Z(x)$：归一化因子、分配函数，确保给定x，所有y概率加起来等于1

$$Z(x)=\sum _y{\pi }_{ref}(y\mid x)\exp (\frac{1}{\beta }r(x,y))$$

显示最优解推导过程

显示最优解推导过程

显示最优解推导过程

• 推导1

$$\begin{array}{ll}\underset{{\pi }_{\theta }}{max}J(\theta )& =\underset{{\pi }_{\theta }}{max}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[r_{\varphi }(x,y)-\beta \cdot D_{KL}({\pi }_{\theta }(y\mid x),{\pi }_{ref}(y\mid x))]\\ & =\underset{{\pi }_{\theta }}{max}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[r_{\varphi }(x,y)-\beta \cdot \log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)}]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)}-\frac{1}{\beta }\cdot r_{\varphi }(x,y)]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)}-\log e^{\frac{r_{\varphi }(x,y)}{\beta }}]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)\cdot e^{r_{\varphi }(x,y)/\beta }}]\\ \end{array}$$

• 归一化分母，构建$Z(x)$，以及新的概率分布${\pi }^{\ast }(y\mid x)$

  $$Z(x)=\sum _y{\pi }_{ref}(y\mid x)\cdot e^{r_{\varphi }(x,y)/\beta }$$$${\pi }^{\ast }(y\mid x)=\frac{{\pi }_{ref}(y\mid x)\cdot e^{r_{\varphi }(x,y)/\beta }}{Z(x)}$$

• 代入目标式子，得到KL散度

$$\begin{array}{ll}\underset{{\pi }_{\theta }}{max}J(\theta )& =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{\frac{{\pi }_{ref}(y\mid x)\cdot e^{r_{\varphi }(x,y)}/\beta }{Z(x)}\cdot Z(x)}]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }^{\ast }(y\mid x)}-\underset{\mathrm{与}{\pi }_{\theta }\mathrm{无}\mathrm{关}}{\underbrace{\log Z(x)}}]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim D,y\sim {\pi }_{\theta }(y\mid x)}[\log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }^{\ast }(y\mid x)}]\\ & =\underset{{\pi }_{\theta }}{min}{E}_{x\sim \mathcal{D}}{D}_{KL}({\pi }_{\theta }(y\mid x),{\pi }^{\ast }(y\mid x))\end{array}$$

• KL散度在2个分布相等时取最小值，因此RLHF训练希望得到的最优概率分布就是${\pi }^{\ast }(y\mid x)$

$${\pi }^{\ast }(y\mid x)=\frac{{\pi }_{ref}(y\mid x)\cdot e^{r_{\varphi }(x,y)/\beta }}{Z(x)}$$

反解奖励函数

反解奖励函数

反解奖励函数

• 直接转换${\pi }^{\ast }(y\mid x)$定义，反解出隐式奖励函数$r_{\varphi }(x,y)$

$$\frac{{\pi }^{\ast }(y\mid x)}{{\pi }_{ref}(y\mid x)}\cdot Z(x)=e^{r_{\varphi }(x,y)/\beta }$$$$\beta \cdot \log \frac{{\pi }^{\ast }(y\mid x)}{{\pi }_{ref}(y\mid x)}\cdot Z(x)=r_{\varphi }(x,y)$$$$r_{\varphi }(x,y)=\beta \cdot \log \frac{{\pi }^{\ast }(y\mid x)}{{\pi }_{ref}(y\mid x)}+\beta \cdot \log Z(x)$$

DPO和RM目标loss一致

RM&DPO 目标loss一致

奖励函数带入奖励loss

• RewardModel 训练目标 和 DPO 训练目标一致

$$\begin{array}{ll}{J}_{RM}& =\underset{r_{\varphi }}{max}{E}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (r_{\varphi }(x,y_w)-r_{\varphi }(x,y_l))]\\ & =\underset{{\pi }^{\ast }}{max}{E}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (\beta \cdot \log \frac{{\pi }^{\ast }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)}+\beta \cdot \log Z(x)-\beta \cdot \log \frac{{\pi }^{\ast }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)}-\beta \cdot \log Z(x))]\\ & =\underset{{\pi }^{\ast }}{max}{E}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (\beta \cdot \log \frac{{\pi }^{\ast }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)}-\beta \cdot \log \frac{{\pi }^{\ast }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)})]\\ & =J_{DPO}\end{array}$$

DPO目标和Reward Model一致

• DPO对标的是RewardModel
  • 训练数据一致、loss函数一致，局限性也一致。

$$J_{DPO}=J_{RM}$$

DPO和RM不同点

• 架构不同
  • RM：有单独的Value Head，输出分值
  • DPO：无Value Head，直接优化token概率
• 优化手段/目标不同
  • RM：优化偏序打分目标
  • DPO：优化生成目标。

DPO和RM 联系

• RM可以给DPO扩充数据
• 理论上，RM也可以做生成，DPO也可以做打分，只是没这么试过。

DPO 核心思想

DPO 核心思想

通过${\pi }_{\theta },{\pi }_{old}$反解出奖励函数

• 逆向运用理论最优解关系。
• 不再采用老策略：先学习奖励函数、再利用奖励函数优化策略。
• 假设LLM隐式定义一个奖励函数，从策略${\pi }_{\theta }$和参考策略${\pi }_{ref}$中反解出隐式奖励函数

$$r_{\varphi }(x,y)=\beta \cdot \log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)}+\beta \cdot \log Z(x)$$

偏好建模

• winner > loser, chosen > reject
• 人类偏好$y_w$而不是$y_l$的概率 $p(y_w>y_l\mid x)$

$$\begin{array}{ll}p(y_w>y_l\mid x)& =\sigma (r(x,y_w)-r(x,y_l))\\ & =\sigma (\beta \cdot \log (\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)})+\beta \cdot \log (Z(x))-\beta \cdot \log (\frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)})-\beta \cdot \log (Z(x)))\\ & =\sigma (\beta \cdot \log (\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)})-\beta \cdot \log (\frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)}))\end{array}$$

DPO 目标函数

• 最小化目标函数

  • $-\log$：交叉熵loss，对错误概率进行惩罚；目标：最小化惩罚
  $${\mathcal{L}}_{DPO}({\pi }_{\theta };{\pi }_{ref})=-{\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\log \sigma (\beta \cdot \log (\frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)})-\beta \cdot \log (\frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)}))]$$

• 最大化以下目标

  • 生成正样本的概率 比参考模型高，生成负样本的概率 比参考模型低。

$$\underset{\theta }{max}\log \sigma (\beta \cdot \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)}-\beta \cdot \log \frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)})$$

从loss理解其弊端

• Loss转换过程

$$\begin{array}{ll}\underset{\theta }{max}{J}_{DPO}(\theta )& =\underset{\theta }{max}\log \sigma (\beta \cdot \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{ref}(y_w\mid x)}-\beta \cdot \log \frac{{\pi }_{\theta }(y_l\mid x)}{{\pi }_{ref}(y_l\mid x)})\\ & =\underset{\theta }{max}\log \sigma (\beta \log {\pi }_{\theta }(y_w\mid x)-\beta \log {\pi }_{ref}(y_w\mid x)-\beta \log {\pi }_{\theta }(y_l\mid x)+\beta \log {\pi }_{ref}(y_l\mid x))\\ & =\underset{\theta }{max}\log \sigma (\beta \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\theta }(y_l\mid x)}-\beta log\frac{{\pi }_{ref}(y_w\mid x)}{{\pi }_{ref}(y_l\mid x)})\end{array}$$

• Loss转换结果

  • 生成正负样本的比例，要目标策略的比例比参考策略的比例 高，loss就可以下降。
  $$\underset{\theta }{max}\log \sigma (\beta \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\theta }(y_l\mid x)}-\beta \log \frac{{\pi }_{ref}(y_w\mid x)}{{\pi }_{ref}(y_l\mid x)})$$

  • 比如参考策略：$\frac{0.5}{0.25}=2$，目标策略 $\frac{0.3}{0.1}=3$，

    • 虽然loss下降、负样本概率下降，但是正样本概率也下降了。
    • 正负样本概率都下降，自然一些奇奇怪怪的输出概率就提高了。
    $${\pi }_{ref}:\frac{0.5}{0.25}=2\to {\pi }_{\theta }:\frac{0.3}{0.1}=3$$

梯度更新

$${\mathrm{\nabla }}_{\theta }{\mathcal{L}}_{DPO}({\pi }_{\theta };{\pi }_{ref})=-\beta \cdot {\mathbb{E}}_{(x,y_w,y_l)\sim \mathcal{D}}[\underset{\mathrm{权}\mathrm{重}：\mathrm{模}\mathrm{型}\mathrm{犯}\mathrm{错}\mathrm{越}\mathrm{大}，\mathrm{权}\mathrm{重}\mathrm{越}\mathrm{高}}{\underbrace{\sigma ({\hat{r}}_{\theta }(x,y_l)-{\hat{r}}_{\theta }(x,y_w)}})\cdot \underset{\mathrm{方}\mathrm{向}：\mathrm{增}\mathrm{加}{y}_w\mathrm{似}\mathrm{然}，\mathrm{降}\mathrm{低}{y}_l\mathrm{似}\mathrm{然}}{\underbrace{({\mathrm{\nabla }}_{\theta }\log \pi (y_w\mid x)-{\mathrm{\nabla }}_{\theta }\log \pi (y_l\mid x))}}]$$$${\hat{r}}_{\theta }(x,y)=\beta \cdot \log \frac{{\pi }_{\theta }(y\mid x)}{{\pi }_{ref}(y\mid x)}$$

算法机制

• 数据：离线静态的偏好数据
• 参考模型作用：${\pi }_{\theta }$和${\pi }_{ref}={\pi }_{sft}$不要偏离太远
• 超参数$\beta$：控制2部分权重
  • 一是：最大化chosen和reject之间的概率差
  • 二是：保持与参考模型的相似性

DPO 缺点

简洁性是其最大优点，但也是其最大缺点。

DPO 缺陷

1. 离线模式缺乏在线采样数据

• 策略模型在进化，但静态偏好数据一成不变

  • 数据集无法代表 新策略潜在的失败模式，导致模型无法从新的错误中学习。

  • DPO离线特性限制了模型的探索能力。

    • 只有evaluate，没有generate

  • PPO/GRPO 会一直和环境交互采样数据，用当前策略采样新数据 来学习提升。

    • generate + evaluate + generate + evaluate + ...

2. DPO Loss 导致优化过程不稳定

• loss 见上文 DPO 核心思想

$$\underset{\theta }{max}\log \sigma (\beta \log \frac{{\pi }_{\theta }(y_w\mid x)}{{\pi }_{\theta }(y_l\mid x)}-\beta \log \frac{{\pi }_{ref}(y_w\mid x)}{{\pi }_{ref}(y_l\mid x)})$$

• 正样本概率、负样本概率 都可能会下降。 回答抑制模式，正负似然都下降。

• 奇怪输出概率会上升，特别在遇见未见内容时。

• 负样本概率下降比正样本概率提升 快得多。

  • 大力惩罚已知坏样本，擅长学习不做什么，而非做什么。
  • 不是探索奖励好样本。

• 过拟合/RewardHacking

  • Loss对所有偏好对一视同仁，不会做权重区分，强行拉开他们的概率差距
  • 缺乏鲁棒性：可能拟合数据噪声，而非真实人类偏好。

3. 依赖SFT模型和数据质量

• 对SFT模型质量很敏感
  • 最终性能取决于初始化SFT模型。
  • 起点差了，就很难摆脱。而在线学习能通过采样自我学习迭代来摆脱。
• 数据质量敏感
  • 需要高质量偏好数据
  • 可能学习多数群体的偏好、而忽略少数群体的观点，引入偏见。

GRPO

PPO缺点&GRPO动机

PPO 缺点 & GRPO 动机

PPO 核心思想

• Actor Model

$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=E_{q,o\sim {\pi }_{{\theta }_{old}}}\frac{1}{|o|}\sum _{t=1}^{|o|}min(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})}\cdot A_t,\mathrm{clip}(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})},1-ϵ,1+ϵ)\cdot A_t)$$

• Critic Model

$$\begin{array}{ll}{L}_{\mathrm{c}\mathrm{r}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{c}}& =(\underset{TD\mathrm{目}\mathrm{标}，\mathrm{增}\mathrm{加}GAE}{\underbrace{r_{t+1}+\gamma V_{old}(s_{t+1})+\gamma \lambda A_{t+1}^{GAE}(s_{t+1},a_{t+1})}}-\underset{\mathrm{最}\mathrm{新}\mathrm{网}\mathrm{络}\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\mathrm{n}\mathrm{e}\mathrm{w}}(s_t)}}{)}^2\end{array}$$

• Reward Model （不参与训练，或 Rule Based Reward）

$$r_t^{\text{total}}=r_t^{\text{env}}-{\text{KL}}_t({\pi }_{\theta },{\pi }_{ref})=r_t^{\text{env}}-\beta \cdot \log \frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{ref}(o_t\mid q,o_{<t})}$$

PPO 缺点

• 资源开销大
  • 需要训Critic Model(通常和Actor同尺寸)，增加了额外的内存和计算开销。
  • 每个Token都需要由Critic 去估计价值, $A_t$ 依赖Critic。
• 训练复杂/不好训
  • LLM通常只有最后一个Token才有奖励信号
  • 导致Critic Model 难以估计每个Token的价值，不好训练。

GRPO 动机

• 解决PPO Critic资源开销大、训练复杂的问题。

GRPO核心思想

GRPO 核心思想

核心思想

• 抛弃Critic Model，降低资源开销和 训练复杂度。

• 分组采样：每个Prompt采样1组答案(G=64)。

• 组内计算优势

  • 好的答案，加大权重；差的答案，降低权重。
  • 使用组内平均分作为基线
  • 每个答案，得分减去平均分，作为自身优势，作为策略梯度优化信号。
    • 更多信号见：策略梯度权重设计

• 自适应加权的对比学习。

MC采样思想

• 和REINOFRCE 算法挺像，主要依赖MC采样，不用TD估计优势。
• 但MC采样方差大，没有TD去平衡方差，怎么解呢？
  • 使用组内标准化奖励，一定程度降低了策略梯度估计方差。

组内相对优势

优势计算

分组采样

• 对每个query，采样1组输出，RewardModel 为每个输出打分，给出奖励。

$$q\to \mathbf{o}=\{o_1,o_2,\cdots ,o_G\}\to \mathbf{r}=\{r_1,r_2,\cdots ,r_G\}$$

• 组内基线计算：组内平均奖励/奖励标准差

$$\text{mean}(\mathbf{r}),\text{std}(\mathbf{r})$$

相对组优势计算

• 为每个输出$o_i$，计算组内的相对得分，作为组内的相对优势

$${\hat{r}}_i=\frac{r_i-\text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}\to {\hat{A}}_i={\hat{r}}_i$$

• ${\hat{A}}_{i,t}$ 组内相对优势
  • 不同于PPO仅最后时刻token有奖励信号。
  • 所有时刻的token $o_{t\le T}$，都使用同一个 组内相对得分，作为t时刻优势信号

$${\hat{A}}_{i,t}={\hat{A}}_i={\hat{r}}_i=\frac{r_i-\text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}$$

GRPO策略目标

GRPO 策略目标

优化目标-PPO核心差异

• 使用组内优势来替代GAE优势。
• 把${\pi }_{\theta }$和${\pi }_{{\theta }_{ref}}$的KL约束放入目标函数。
  • PPO是放在每个Token的即时奖励信号 $r_t$里的
    • $r_t^{\text{total}}=r_t^{\text{env}}-\beta \cdot {D_{\text{KL}}}_t({\pi }_{\theta },{\pi }_{ref})$
• 同PPO一样，使用CLIP信任域来保证新旧策略分布差异不太大。

GRPO 优化目标公式

$$J_{\mathrm{G}\mathrm{R}\mathrm{P}\mathrm{O}}({\pi }_{\theta })=E_{q,\{o_i{\}}_{i=1}^G\sim {\pi }_{{\theta }_{old}}}\frac{1}{G}\sum _{i=1}^G\frac{1}{|o_i|}\sum _{t=1}^{|o_i|}(min(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})}\cdot {\hat{A}}_{i,t},\text{clip}(\frac{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{{\theta }_{old}}(o_{i,t}\mid q,o_{i,<t})},1+ϵ,1-ϵ)\cdot {\hat{A}}_{i,t})-\beta \cdot D_{KL}({\pi }_{\theta },{\pi }_{{\theta }_{ref}}))$$

• GRPO梯度， 省去了clip，DAPO token-level loss, VAPO 解决长度不一问题

$${\mathrm{\nabla }}_{\theta }{J}_{\text{GRPO}}(\theta )=E_{x\in \mathcal{D},\{y_i{\}}_{i=1}^G\sim {\pi }_{{\theta }_{old}}(\cdot |x)}[\frac{1}{G}\sum _{i=1}^G\underset{\mathrm{序}\mathrm{列}\mathrm{内}\mathrm{平}\mathrm{均}}{\underbrace{\frac{1}{|y_i|}\sum _{t=1}^{|y_i|}}}\underset{\text{token重要性权重}}{\underbrace{\frac{{\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}{{\pi }_{{\theta }_{old}}(y_{i,t}|x,y_{i,<t})}}}\cdot \underset{\text{token优势}}{\underbrace{{\hat{A}}_{i,t}}}\cdot \underset{\text{token梯度}}{\underbrace{{\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(y_{i,t}|x,y_{i,<t})}}]$$

GRPO ref KL 约束

• K3 KL，无偏且低方差

$${D_{KL}}_t({\pi }_{\theta },{\pi }_{{\theta }_{ref}})=\frac{{\pi }_{ref}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-\log \frac{{\pi }_{ref}(o_{i,t}\mid q,o_{i,<t})}{{\pi }_{\theta }(o_{i,t}\mid q,o_{i,<t})}-1$$

GRPO调参踩坑经验

GRPO 关键点

主要坑点

• 采样基础设施：需高效的推理系统，SGLANG/VLLM
• Group大小：太小(<32)统计不稳定，太大计算贵
• Beta调参：非常关键，需要仔细调
• 奖励设计：需要奖励信号有足够的区分度

GRPO 关键参数

Beta 参数

• 0.05：学习太慢、收敛慢
• 0.1：大多数任务的甜点
• 0.2：有时候会过拟合
• 0.3+：基本上会发散

Group_size

• 16：统计不稳定、方差大
• 32：勉强能用
• 64：比较稳定的选择
• 128：更稳定、但计算成本高

• 来自 PPO vs GRPO 本质区别是什么

GRPO 标准配置

# 我的GRPO标准配置
grpo_config = {
    "learning_rate": 8e-7,    # 比PPO小很多
    "beta": 0.1,              # KL系数，最关键
    "group_size": 64,         # 群体大小
    "temperature": 0.7,       # 生成多样性
    "top_p": 0.9,             # 核采样
    "max_length": 2048,       # 最大长度
}

PPO vs GRPO

GRPO算法和PPO算法本质区别是什么

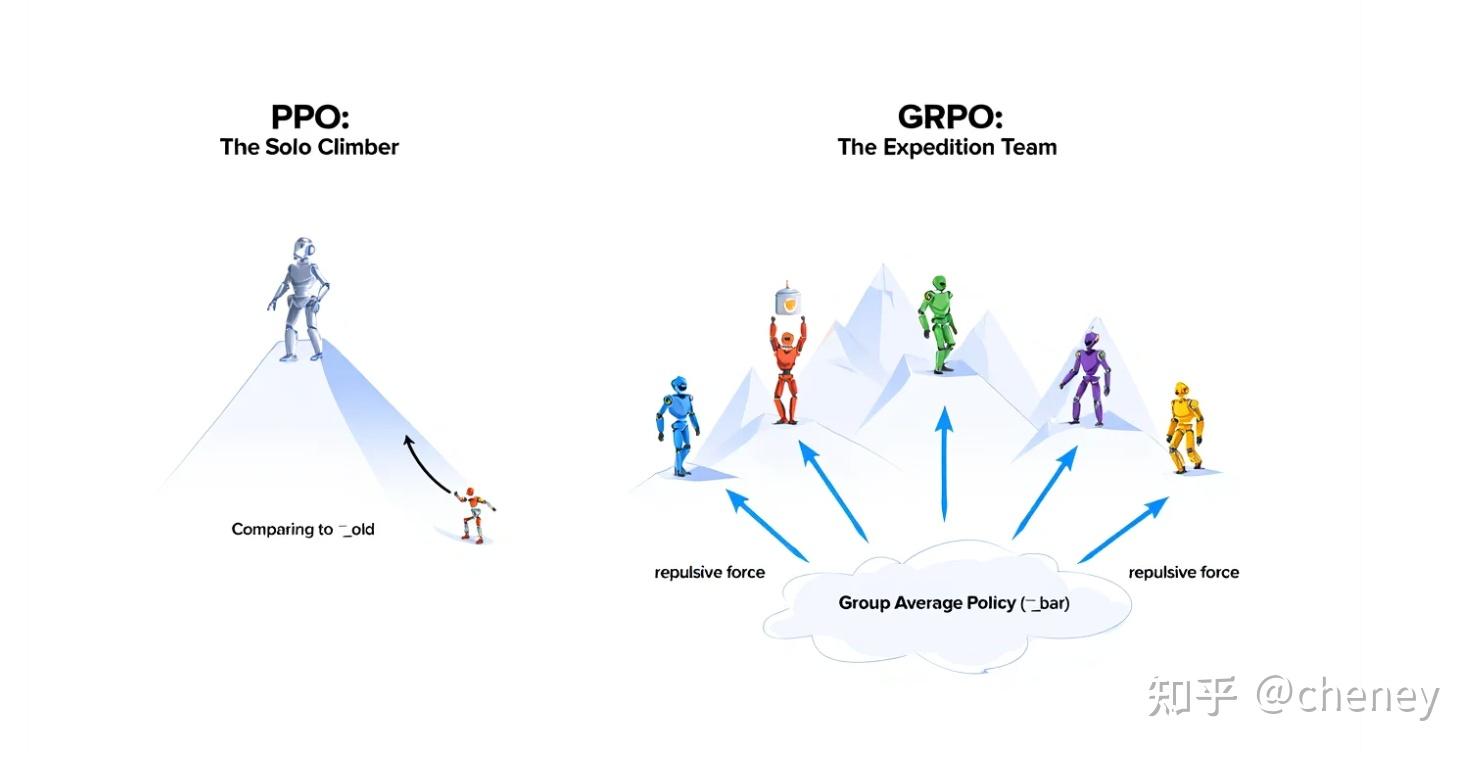
核心目标思想差异

PPO vs GRPO 核心目标

PPO

• 找到一个最大化奖励的最优策略。
• 解决问题：策略更新的稳定性。

GRPO

• 找到一组高质量且多样化的策略。
• 解决问题：策略发现的多样性。

PPO vs GRPO 核心思想

PPO

• 拥有历史数据库的教练，追求绝对最优，学习绝对期望值。
• 过程
  • 策略模型(1个运动员)完成1次表现，奖励模型给出最终成绩。
  • 价值模型基于历史数据，在运动员跑到中间点时，预测最终成绩；
• 优势：
  • 最终成绩-历史预测成绩 。超预期，就获得正向奖励。
  • 参照物：过去的自己，${\pi }_{{\theta }_{old}}$。超越昨天的自己。
• 学习信号/优势信号
  • Token-Level，Critic提供更细粒度的学习信号。
  • 通过Critic，每个token有不同的价值。而不是整个轨迹级别的。

GRPO

• 组织小组赛的教练，追求相对领先，直接使用相对的、动态的平均值。
• 过程
  • 策略模型(1组运动员)同时完成表现，生成G个回答。奖励模型为每位运动员给出最终成绩。
  • 没有历史数据，直接算出这组运动员的平均成绩。
• 优势：
  • 组内相对优势，个人成绩-小组平均成绩。超平均水平，就获得正向奖励。
  • 参照物：团队平均策略，$\overline{\pi }$。超越团队平均。
• 学习信号/优势信号
  • Response-Level，Trajectory-Level
  • 轨迹级优势直接应用到序列的每个token，作为token-level优势。

技术实现差异

PPO vs GRPO 技术实现差异

核心目标

• PPO：找到一个最大化累积奖励的单一最优策略。解决策略更新的稳定性问题。
• GRPO：找到一组高质量且具备多样性的策略。解决策略发现的多样性和效率问题。

优化参照物

• PPO：过去的自己${\pi }_{{\theta }_{old}}$。通过和上一轮策略比较，在信任域内小步快跑，争取超过昨天的自己。
• GRPO：小组的平均策略$\overline{\pi }$。超过平均水平，则获得正向激励。

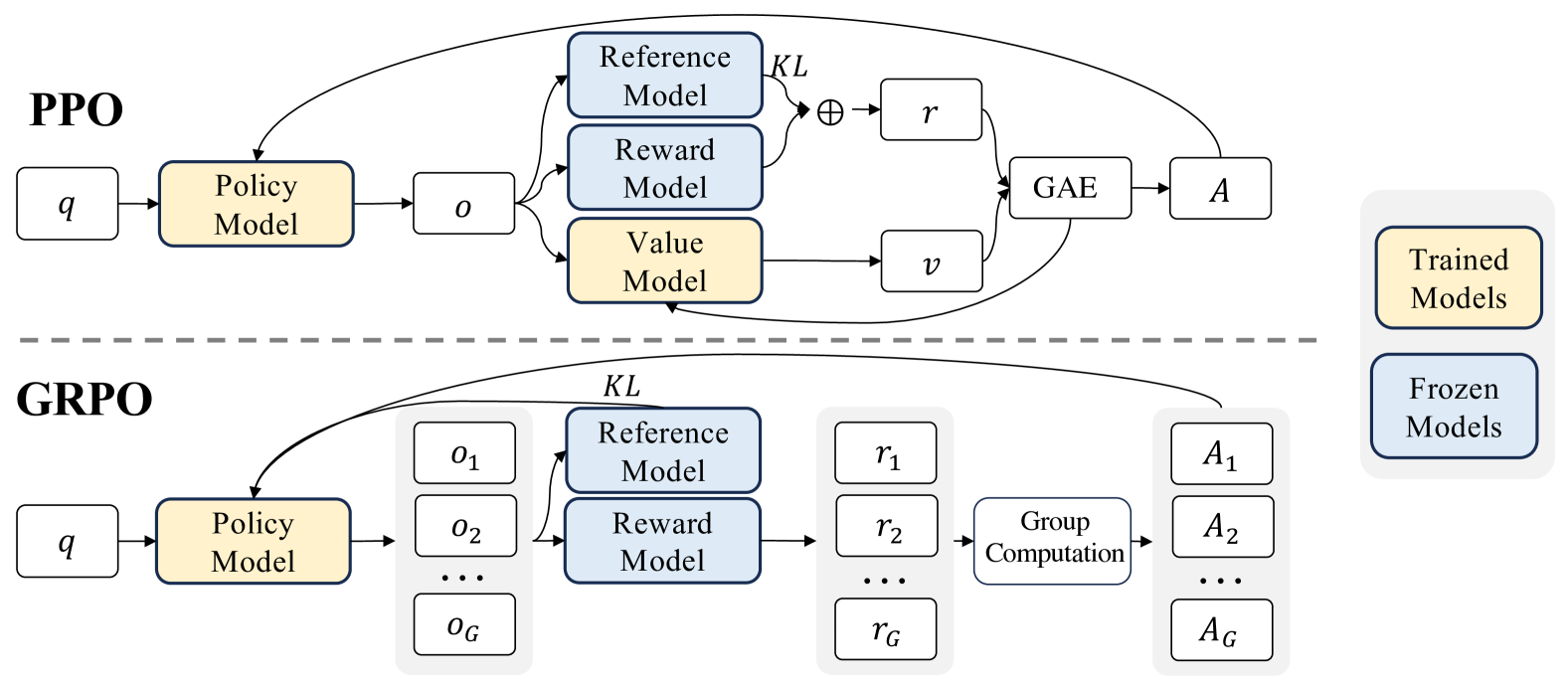
算法架构

• PPO
  • Actor-Critic架构：Actor+Critic+RewardModel。
  • Critic 估计状态价值$V(s)$、用于GAE计算优势。
  • MC 采样 + TD估计。
• GRPO
  • 纯策略梯度：Actor+RewardModel。
  • 无Critic，价值基线通过统计得出。
  • MC 采样。

优势

• PPO
  • GAE，依赖价值模型$V(s)$，基于模型预测、学习的方法。
    • 对多个n步优势估计，加权平均，引入λ平衡方差和偏差
    • 结合了多步MC回报+Critic价值预测，MC采样+TD估计。
    • 依赖准确估计的Critic，这个往往是PPO的难点。
  • 优势获得条件
    • 实际得分比历史预测好，才获得正向奖励。
    • 基于绝对奖励+价值函数预测
  • 优势信号特点
    • 仅最后一个token有环境奖励，其余token为0。
    • 所有token都有KL惩罚奖励。
• GRPO
  • 组相对优势，不依赖价值模型， 基于群体投票、统计的方法。
  • 优势获得条件
    • 个人比组平均成绩好，才获得正向奖励。
    • 组内相对排名和分数
  • 优势信号特点
    • 一条轨迹上所有token共享相同的优势值，都为${\hat{A}}_{i,t}$

奖励信号利用

• PPO

  • Token-Level
  • 间接利用。
    • 环境奖励用来训Critic；再由依赖Critic计算的GAE优势，指导Actor更新优化。
  • 有奖励KL惩罚。
  • 绝对奖励信号。

• GRPO

  • Response-level
  • 直接利用。
    • 奖励信号直接用于计算相对优势，直接用于Actor优化。
  • 无奖励KL惩罚。
  • 标准化组相对奖励。

资源开销和训练复杂度差异

PPO vs GRPO

1. 资源开销

• PPO
  • 资源需求高。Actor和Critic 2个模型。
  • 内存需求：基础模型*3倍
    • Actor *1, Critc *1, 梯度+优化器 *1，旧策略缓存：部分参数。
    • 实际和bs、序列长度有关。
• GRPO
  • 资源需求低，仅Actor模型。
  • 内存需求：基础模型*1.5倍
    • Actor *1，梯度+优化器 *0.5(单网络)。
    • 实际和bs、序列长度有关。
  • 无Critic，与PPO相比，显存需求降低25%。若使用规则，不用RewardModel，降低50%。

2. 训练复杂性

• PPO
  • 复杂性：高。
  • 需同时训Actor和Critic，难度大。超参数敏感。
  • Critic本身难训练，尤其在奖励稀疏的语言模型中，Critic难收敛，导致优势估计不准。
• GRPO：
  • 复杂性：低。
  • 只需训练Actor，调参更容易。
  • 基线是直接从组内得分统计出来的，而非学习来的。过程更简单、稳定。

3. 训练稳定性

• PPO
  • 相对稳定。
  • 通过CLIP信任域机制，限制策略更新幅度，防止“学崩”，保证训练稳定性。
  • GAE在Critic训练良好的情况下，能有效平衡降低方差和偏差。Critic若收敛，训练更稳定。
• GRPO
  • 非常稳定。
  • 组内相对优势，天然对奖励绝对值不敏感，只关心排序，有效降低了方差。
  • 目标函数通样有KL约束，保证策略更新的稳定性。

优缺点对比

PPO vs GRPO 优缺点

优点

• PPO

  • 通用性强。
  • 当样本更新对噪声容忍度较高。

• GRPO

  • 高效轻量。无Critic模型，资源消耗低、训练快。
  • 稳定易用。训练过程更稳定，参数好调。
  • 与偏好奖励模型 (Reward Model) 的相对比较机制完美契合

缺点

• PPO

  • 计算成本高。
  • 训练困难。
  • 对奖励缩放敏感。优势估计受奖励绝对值影响。

• ·GRPO

  • 采样开销可能较高，每次更新需要采样G个输出。G太小，方差大。
  • 对G值敏感：会影响性能和开销平衡。
  • 依赖组内质量多样性：组内样本高度相似情况下，如标准差为0，优势估计会失效，导致梯度为0，更新失效。

为什么GRPO能work

为什么GRPO在LLM下可能更优/能work

• Critic 在LLM 稀疏奖励情况下(仅最后token有奖励信号)，非常难以训练。
• GRPO 完美规避了Critic训练难题。
• GRPO和RewardModel很搭配。
  • RewardModel通过比较谁更好来训练，最擅长做出相对判断；
  • GRPO通过组内选出更好的，而非绝对分数。
  • 机制上契合，使得奖励信号利用更加高效。
• 隐式课程学习
  • 同一个问题，组内样本质量有高有低。
  • 模型通过比较，可以同时学到好的和差的，学习信号更加丰富。
• 高效且稳定。

适用场景对比

PPO vs GRPO 适用场景

PPO

• 通用RL，机器人控制、游戏AI等。
• 主观评价。
• 内存、计算资源充足。
• 追求极致性能提升
• 支持连续和离散动作空间。

GRPO

• 针对LLM的RLHF：GRPO完美契合人类偏好训练的RewardModel。
• 内存、计算资源有限。极致性价比。
• 快速迭代。
• 多样性任务。
• 高效稳定。