策略梯度算法
📅 发表于 2025/08/31
🔄 更新于 2025/08/31
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
rl-theory
#策略梯度
#轨迹概率
#轨迹回报
#对数微分技巧
#梯度上升法
#策略梯度目标函数
#策略梯度loss
#策略函数设计
#logits_p
#权重
#基线
#优势函数
#降低方差
#策略梯度分类
#蒙特卡洛策略梯度
#时序差分策略梯度
#REINFORCE算法
#REINOFRCE++
对策略参数化,直接对策略进行优化。
Value-based RL
先学习价值函数V或Q,根据价值函数间接指导策略改进。Policy-based RL
直接对策略进行优化。没有V或Q做中间商。假设策略连续可微函数;用梯度上升算法 直接对策略参数
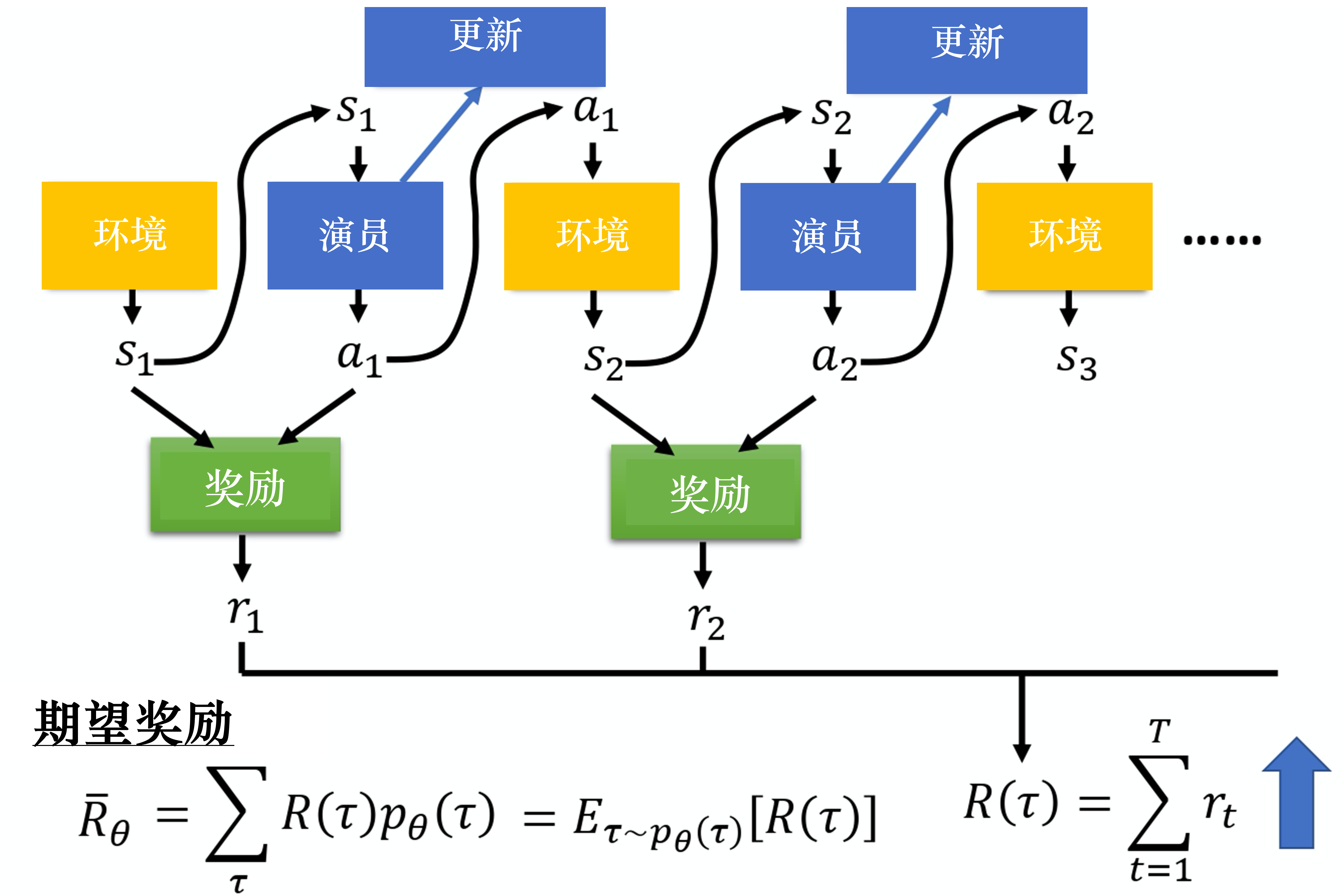
使目标函数所有轨迹回报的期望值。
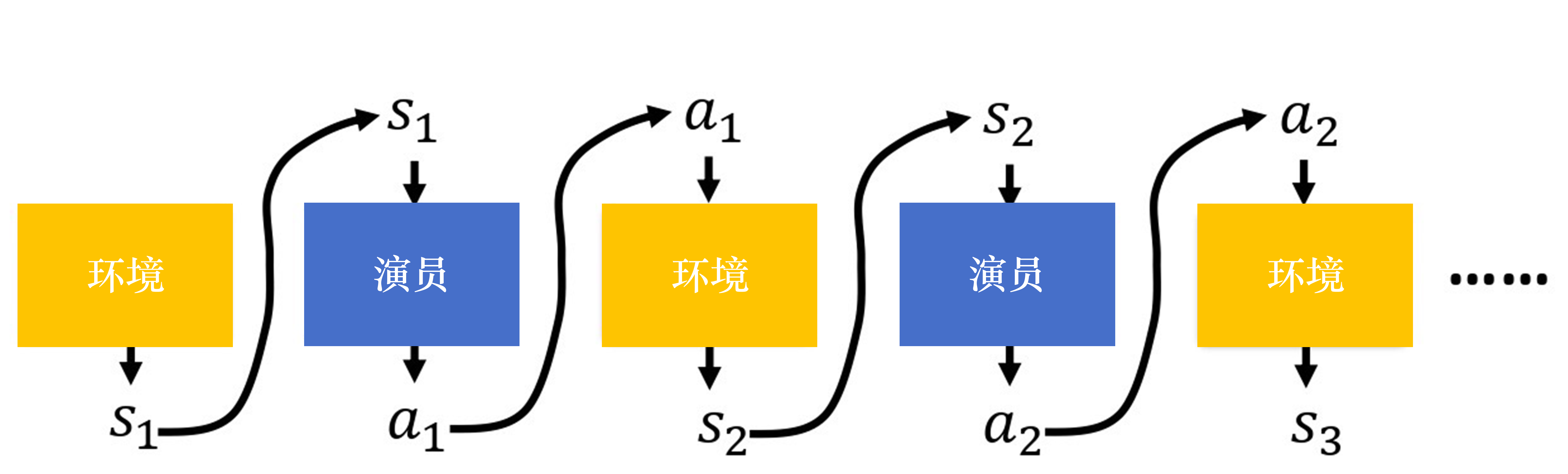
轨迹概率
目标函数
策略的价值期望/期望奖励,所有轨迹回报的期望值。
调整演员内部参数
轨迹奖励
随机变量,非标量,和策略参数依概率选择,有随机性非常不稳定,方差很大。TD&MC 方差和偏差轨迹
目标函数,期望奖励
目标函数
策略梯度定义
策略梯度推导结果
对数定义
导数链式法则
对数乘法公式
对数微分技巧‼️

1. 对数拆解梯度
对数微分,拆解为期望形式2. 细拆轨迹概率梯度
动作策略状态转移概率 去掉无关项3. 采样计算策略梯度
采样N条轨迹、代回细拆项求解最终公式数据采样
采集n条样本,收集每条样本的奖励。需重新采样才能更新模型。梯度计算
计算对数概率 对数概率取梯度,并乘以权重 ,即回报求出整体梯度梯度上升法做参数更新
最大化目标函数 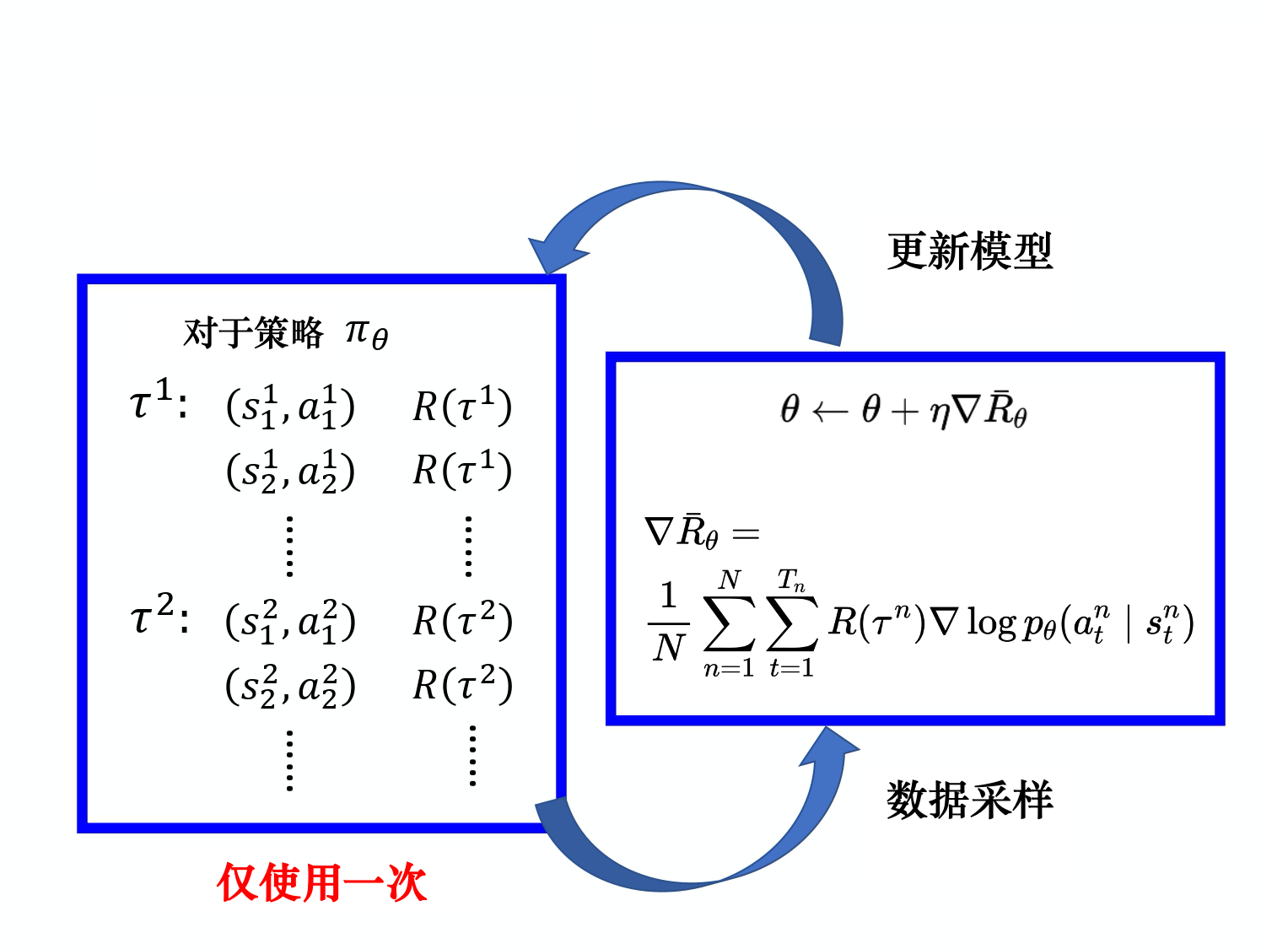
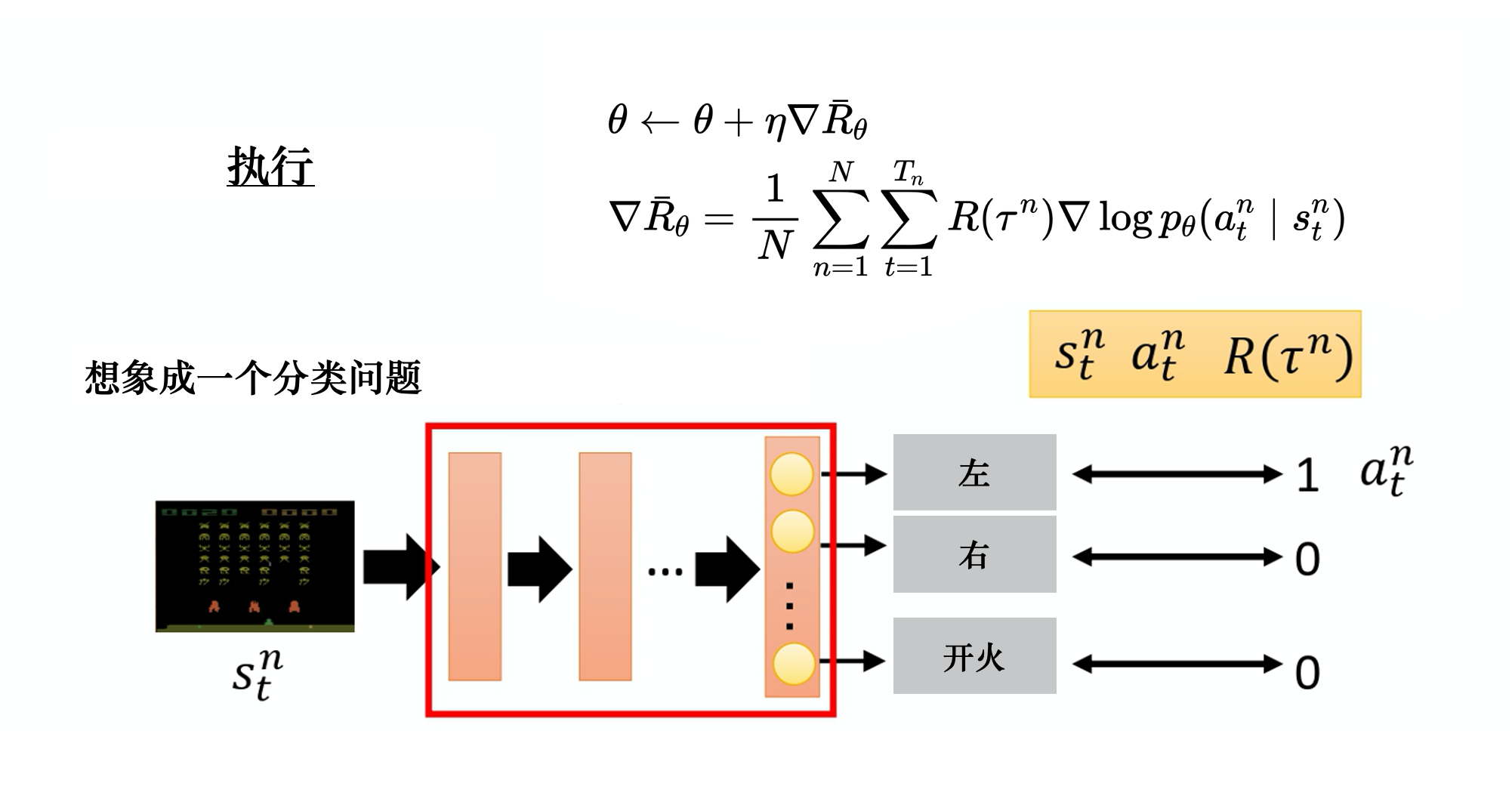
传统交叉熵/监督学习loss
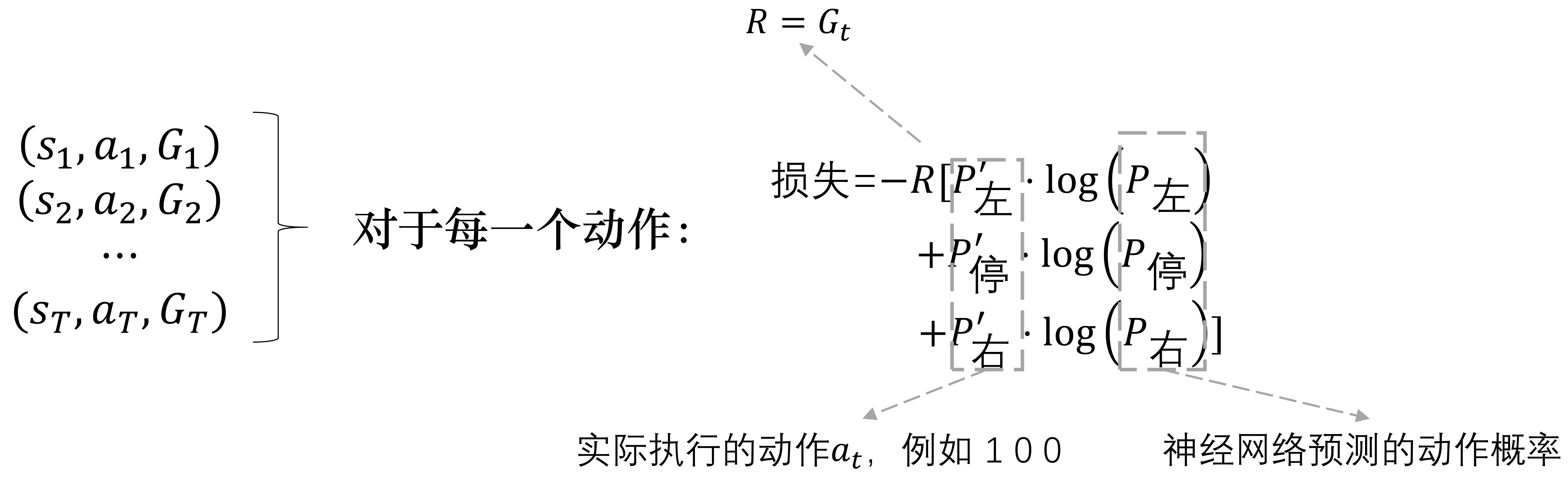
策略梯度loss-轨迹粒度
轨迹回报越高、希望轨迹概率也越高,即二者同分布,使用交叉熵来衡量,非常合适策略梯度loss-动作粒度
奖励回报/优势函数等作为权重,表示动作的好坏。 回报越小,表明动作loss权重应该降低,优化粒度小一点回报越大,表明动作loss权重应该增加,优化粒度大一点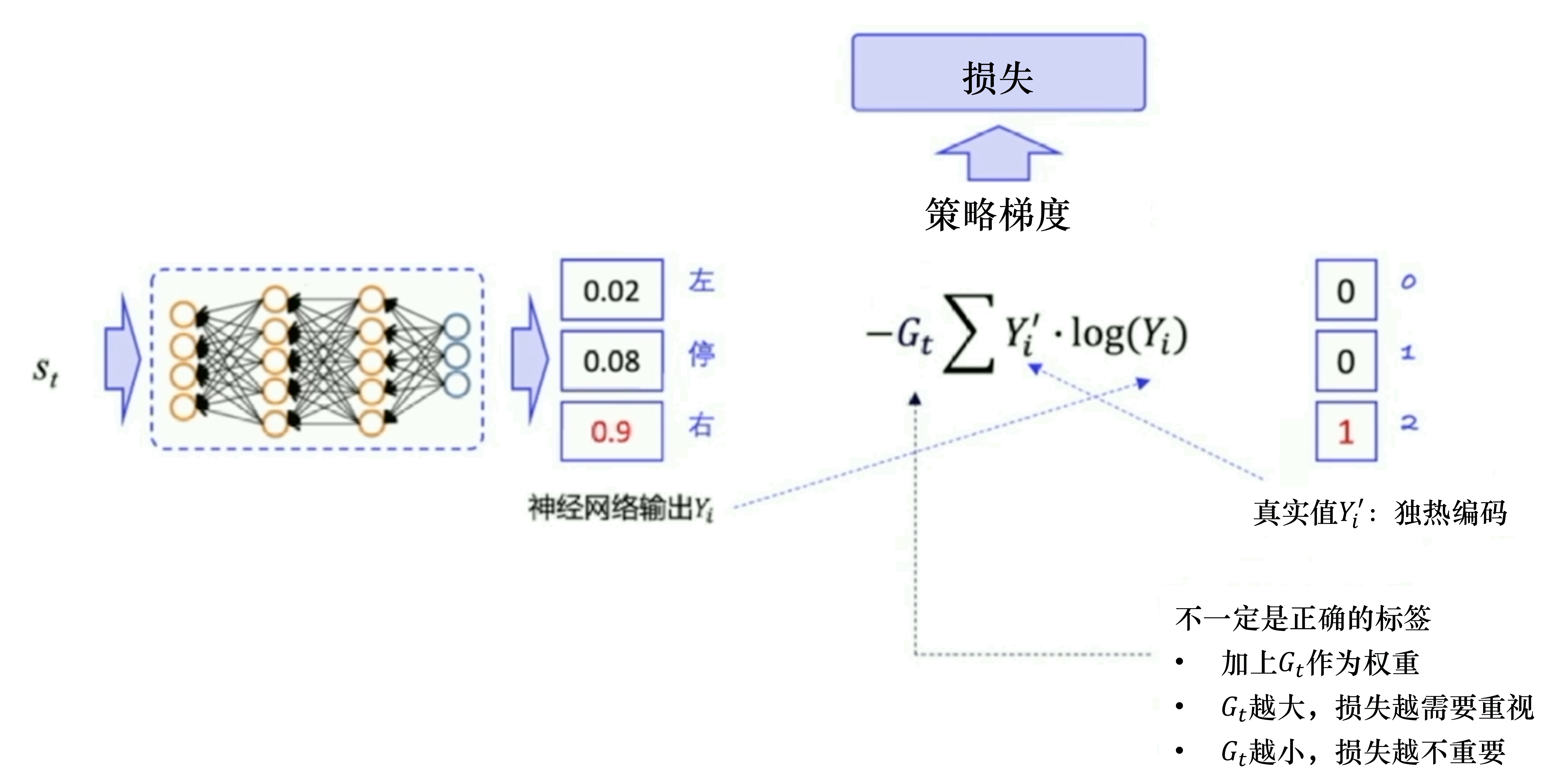
随机策略:输入状态s,输出对应动作概率分布
Softmax计算概率
概率一般
策略梯度如下,一般写作logits_p,对应的 probs,策略动作从高斯分布得出
均值和方差两个值,来构建一个高斯分布,进行采样即可。ActorCritic 存在的问题 (TRPO/PPO来解决)
更新步长选择困难症训练过程比较慢、采样随机性导致可能朝着错误方向更新。有偏的1. 单步奖励
太短视,没看长期回报。永远学不会先苦后甜的策略。2. 完整轨迹回报
高方差权重很大大于0: 提升了采样动作,未采样动作就会下降。所有动作a权重都一样:不公平!需提升概率;有的动作差,贡献少,需要降低概率。3. 总回报
高方差、权重恒大于0[90,110]区间,任何轨迹的总回报非常大的正数。好动作坏动作总回报 1010;更新非常强的正信号。总回报 1005;更新同样非常强的正信号。训练过程不稳定、 收敛很慢。 很难稳定分辨 出好了一点点”。几乎可以忽略不计。很好的动作,但由于没有被采样到自动降低了概率。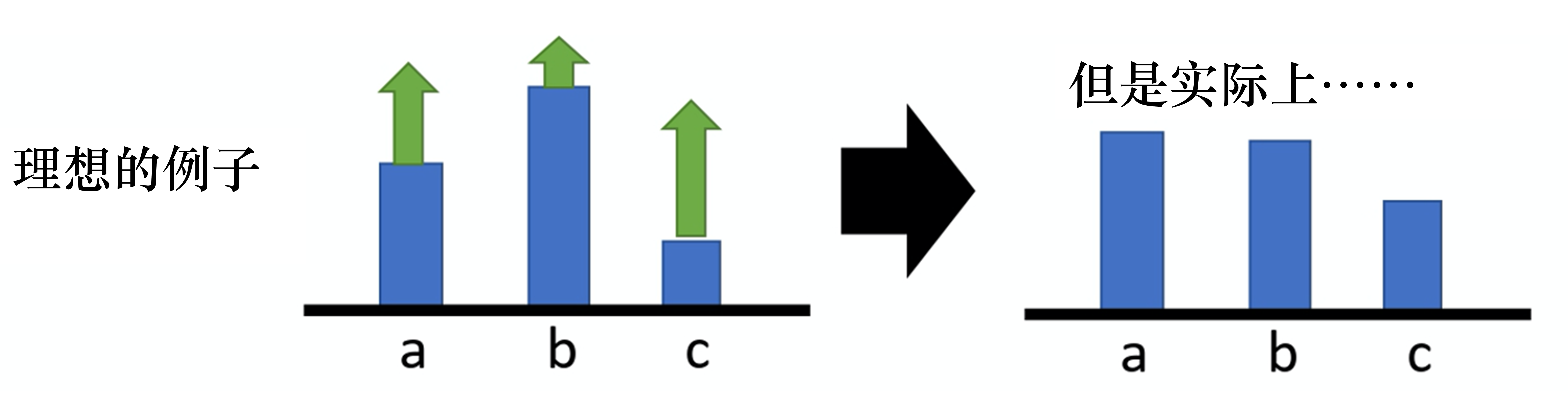
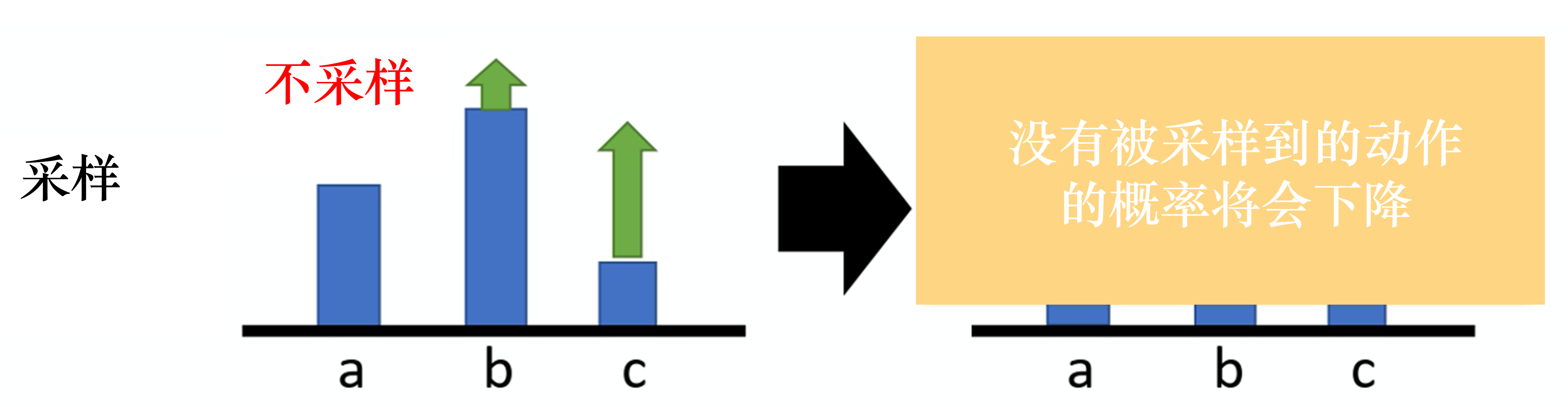
4. 基线/优势函数
减去基线/状态价值函数例子
你考了95分 平均98分;低于平均水平,学习动作需要调整。低方差、高偏差
5. GAE
背景
未采样动作概率更新+方差大。)使其有正有负,降低方差。核心思想
基线函数b,使用新权重 有正有负超过基线,让概率上升低于基线,让概率下降优势函数基线函数b的选择
目的
无偏性:减小方差:核心方法
保证无偏性推导期望:推导可知求解极值点 方差恒为正,是常数;根据上式可知凹函数,必然存在极小值求导数并使其为0,求解出最小值时的取值。代回极值点,求解出最小值结论
方差极小值:背景
鼓励好的动作,抑制差的动作方法1:使用动作时刻t后面的奖励
方法2:使用优势函数
相对于其他动作的优势critic评论员不同动作贡献不同,权重也应该不同:
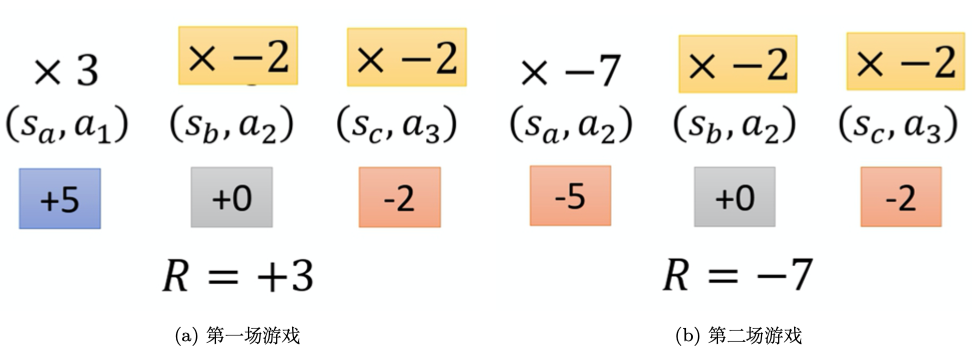
MC 蒙特卡洛方法
回合更新;使用REINFORCE算法TD 时序差分方法
步骤更新;TD估计Q函数,作为权重。Actor-Critic算法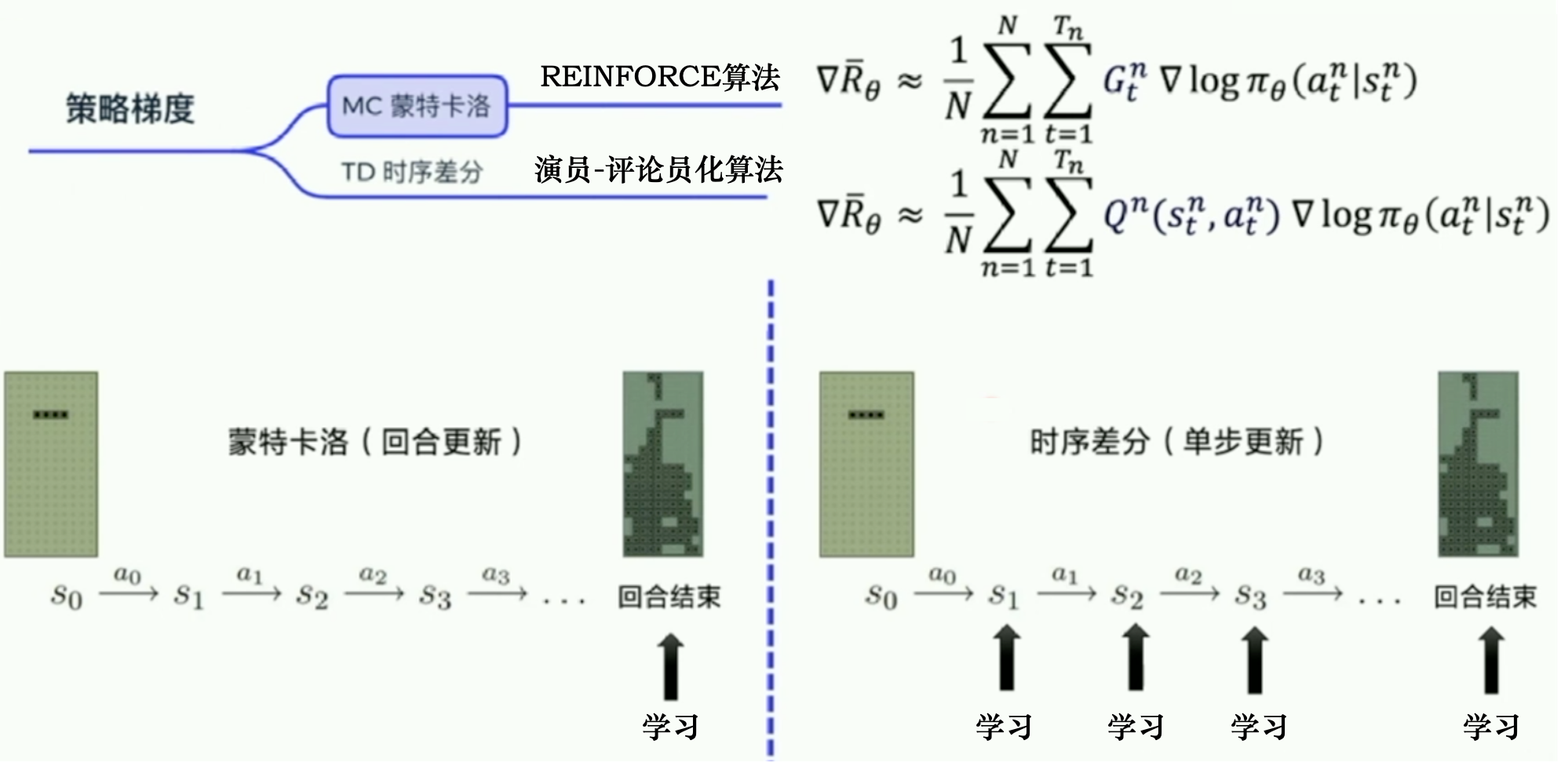
优点 (相比于基于价值的算法)
随机性策略策略梯度是无偏的;基于价值的算法则是有偏的。缺点
采样效率低:MC采样 不如 TD采样高方差:MC高方差,估计梯度时甚至比基于价值的算法方差还高;G很不稳定收敛性差:容易导致局部最优解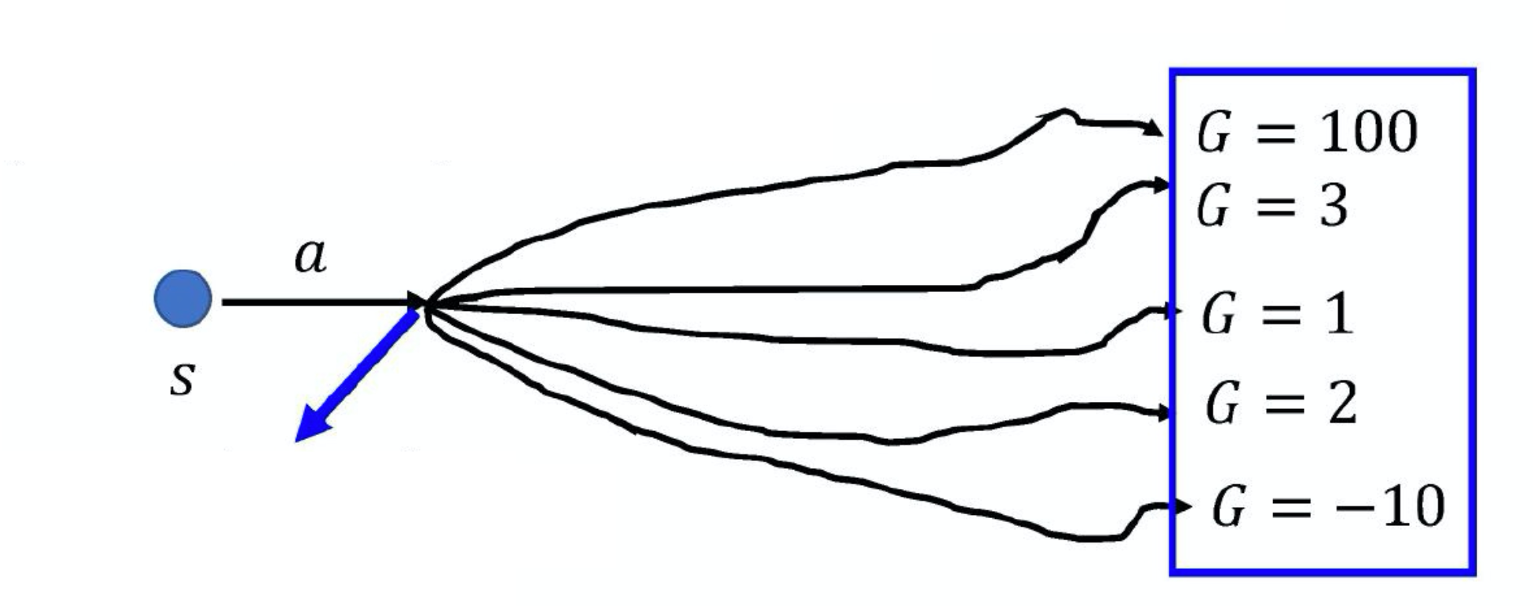
核心思想
一个回合更新一次同策略算法算法步骤
采样一个回合数据;采样后,从0到T每时刻 根据对数概率梯度算法流程
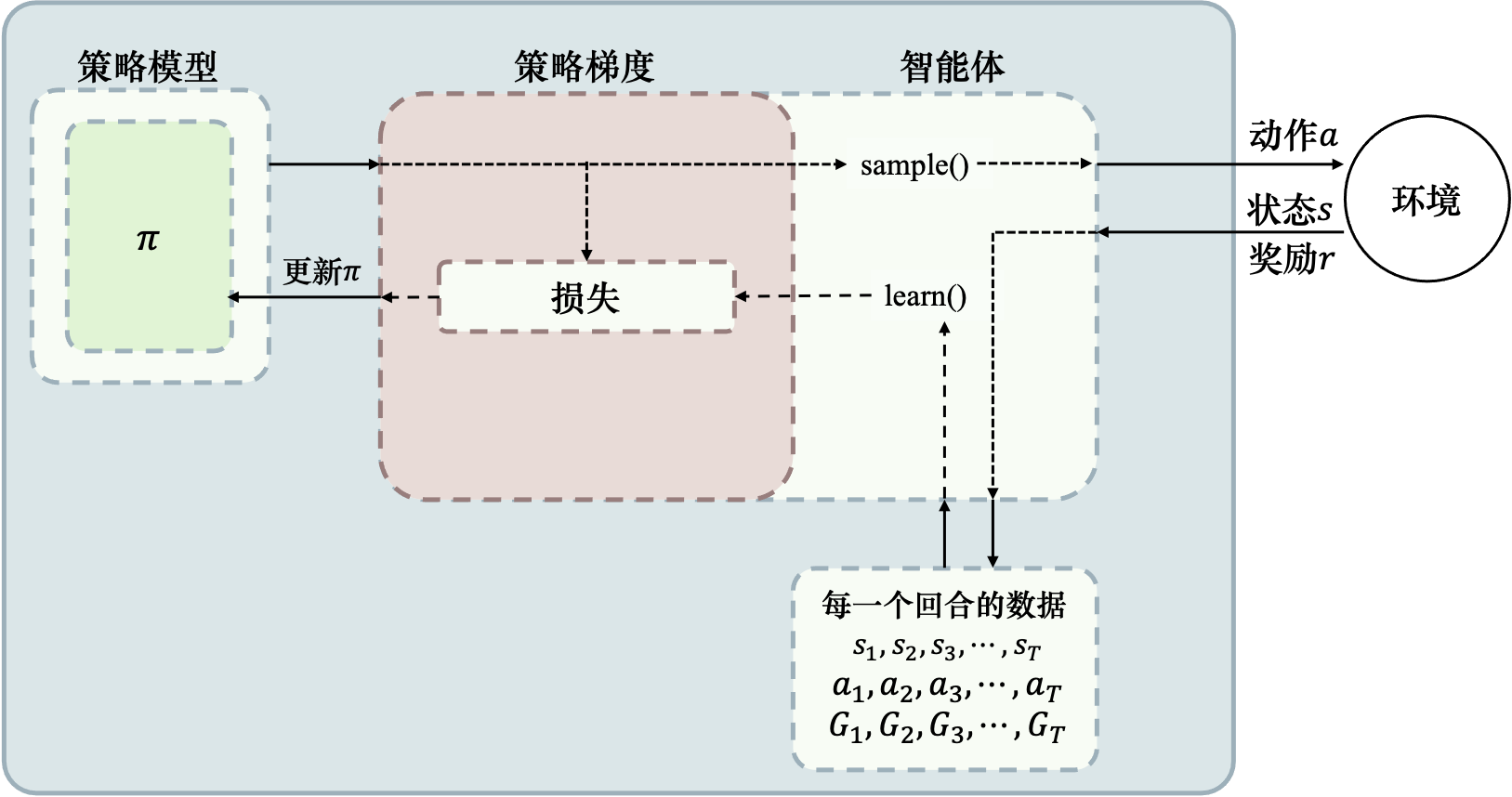
伪代码

具体见笔记:REINFORCE++