确定性策略梯度
📅 发表于 2025/09/01
🔄 更新于 2025/09/01
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
rl-theory
#连续动作
#确定性策略
#随机性策略
#DPG
#DDPG
#TD3
#Actor-Critic
#Q_估计
#Q_target
#目标网络
#经验回放
#OU噪声
#TD3
#双Q网络
#Actor 延迟更新
#Critic 噪声正则化
随机 vs 确定
随机性策略:确定性策略:离散 vs 连续
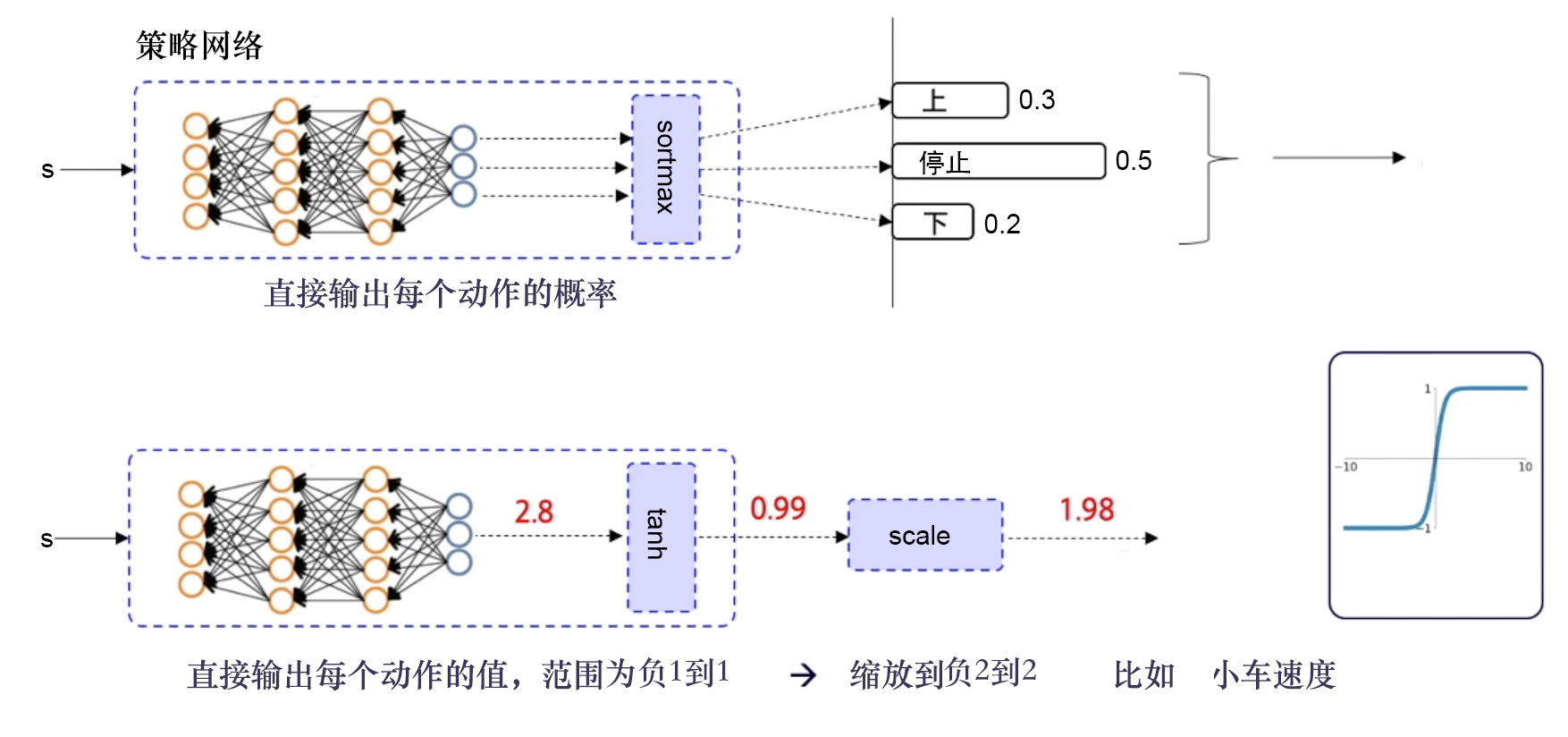
离散动作:输出加softmax,使概率和为1,依概率选择即可连续动作:输出值做缩放到目标区间即可,比如tanh -> [-1, 1], 扩展至小车速度[-2,2],乘以2即可离散动作和连续动作
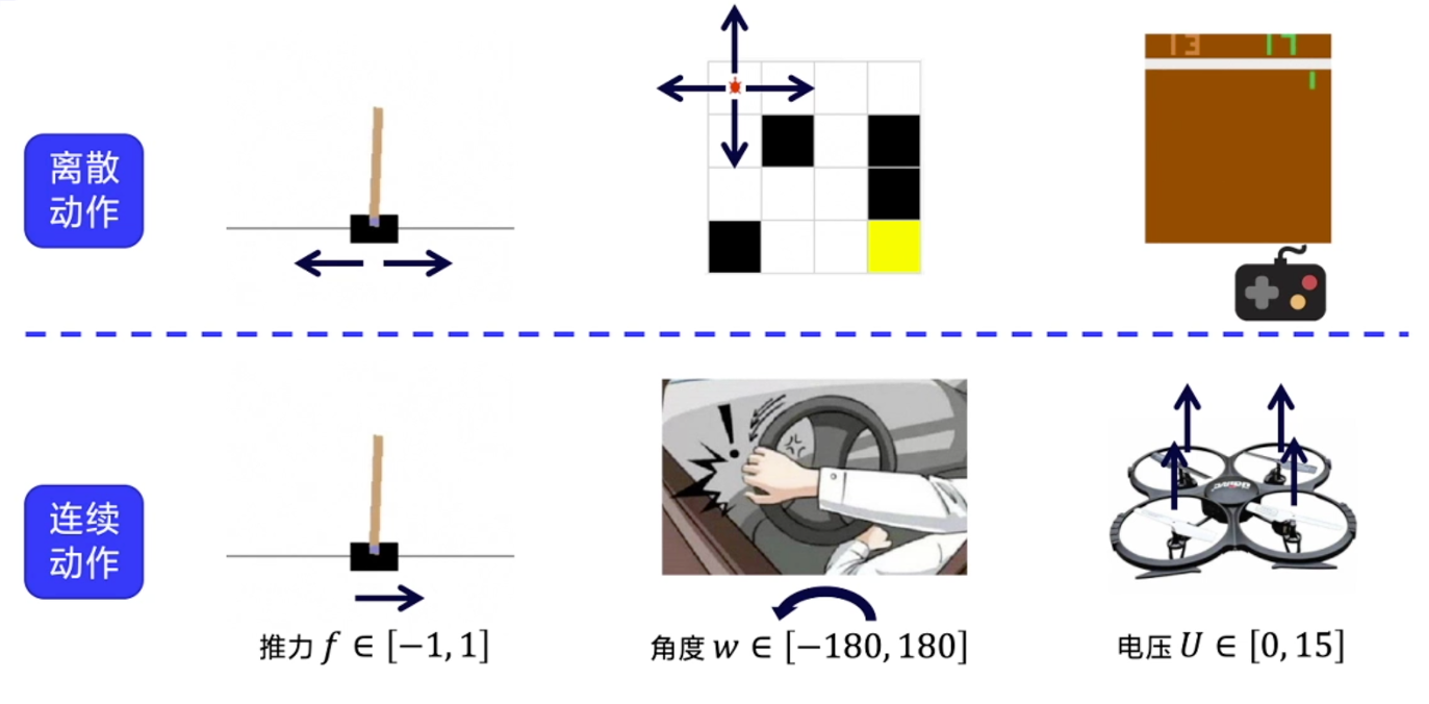
随机性策略、确定性策略。
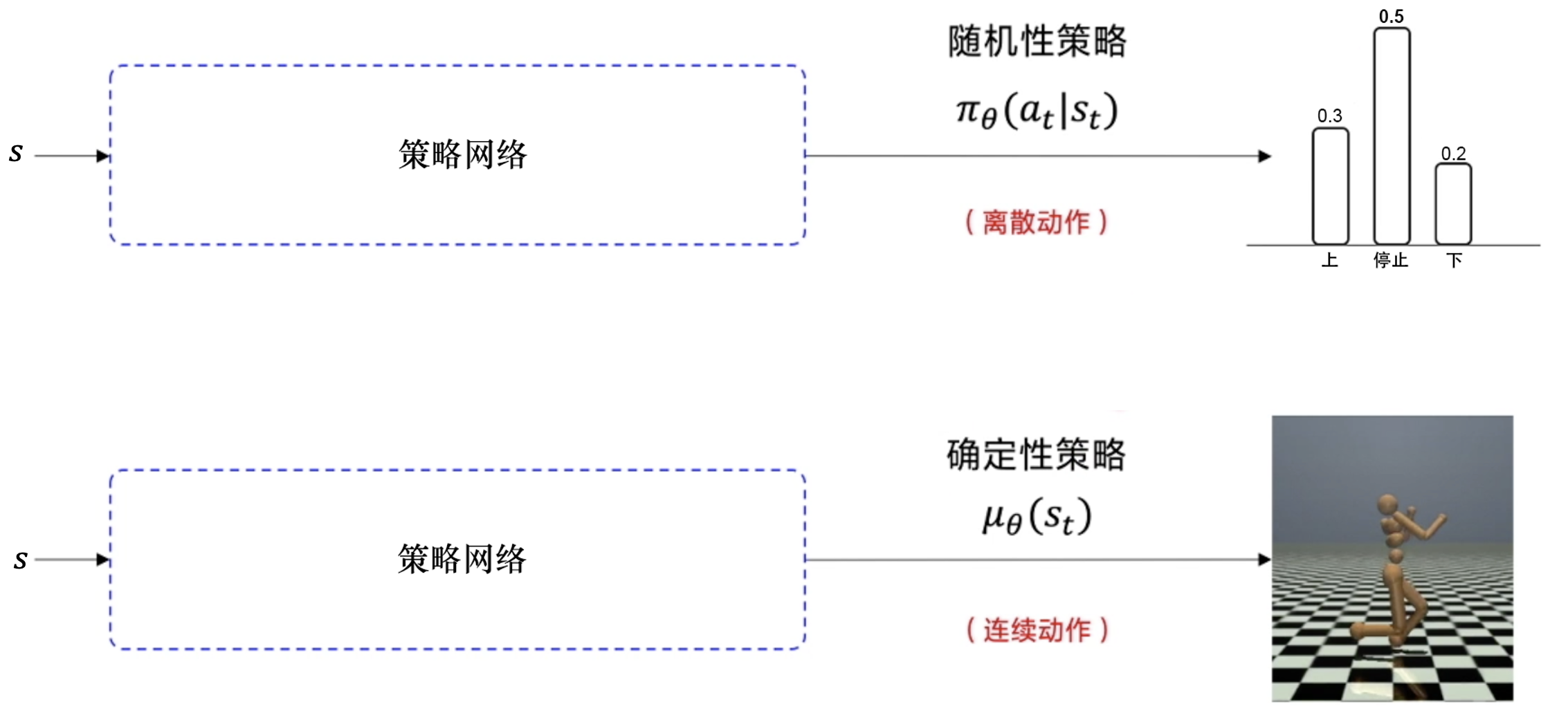
离散、连续动作转换
DDPG的初衷是为了使DQN支持连续动作,架构类似Actor-Critic,但比A3C提出的早1年(2015)。
问题&背景
贪心或argmax间接得到目标:用策略确定性动作核心思想
适配连续动作梯度链式法则,先对a求导,再对梯度上升法来最大化函数Q,得到Q值最大的动作DPG沿用DQN思想,寻找最大Q值动作,没做真正意义上的梯度更新Actor的任务是找到最大Q的a值。
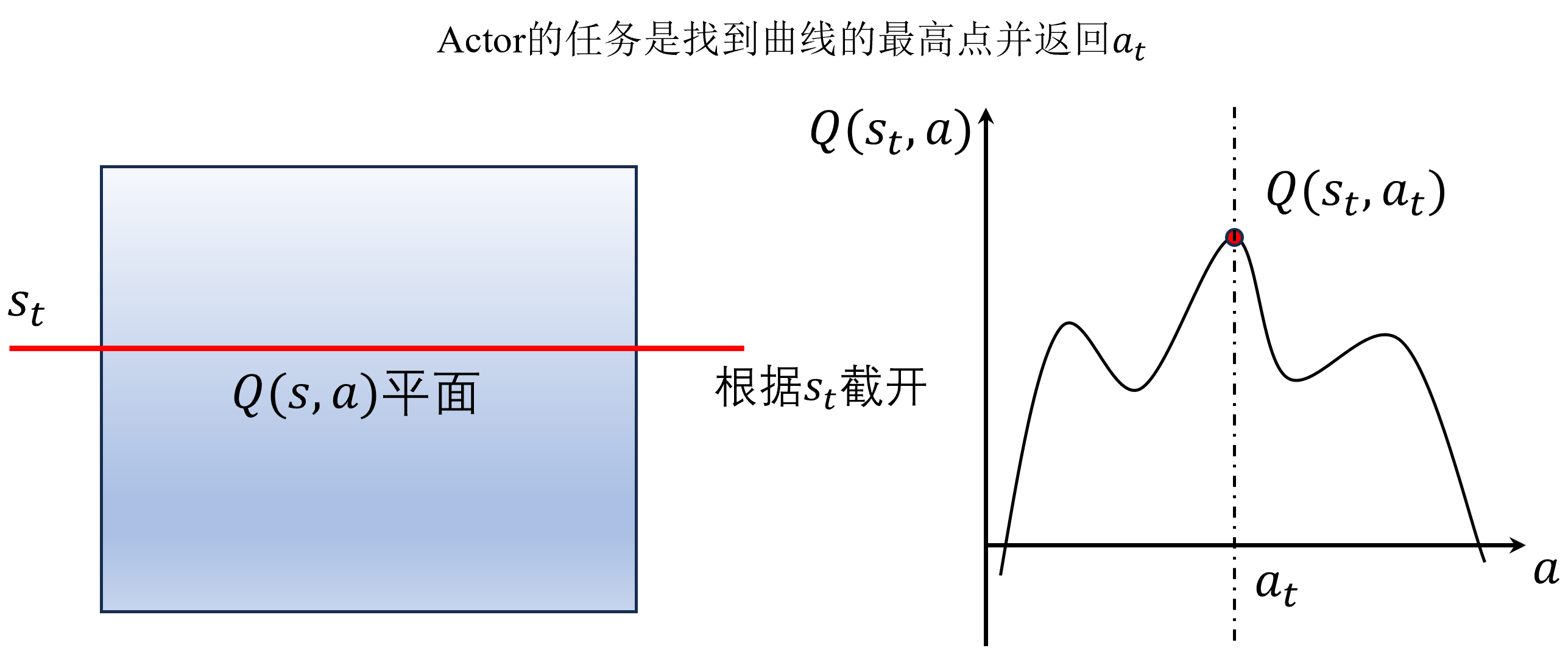
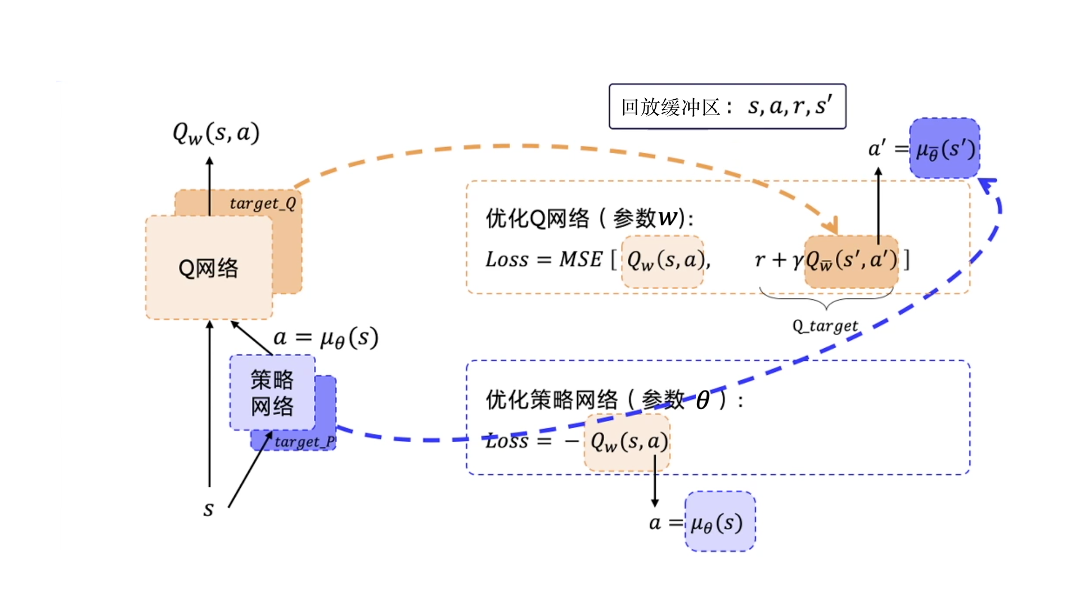
网络结构
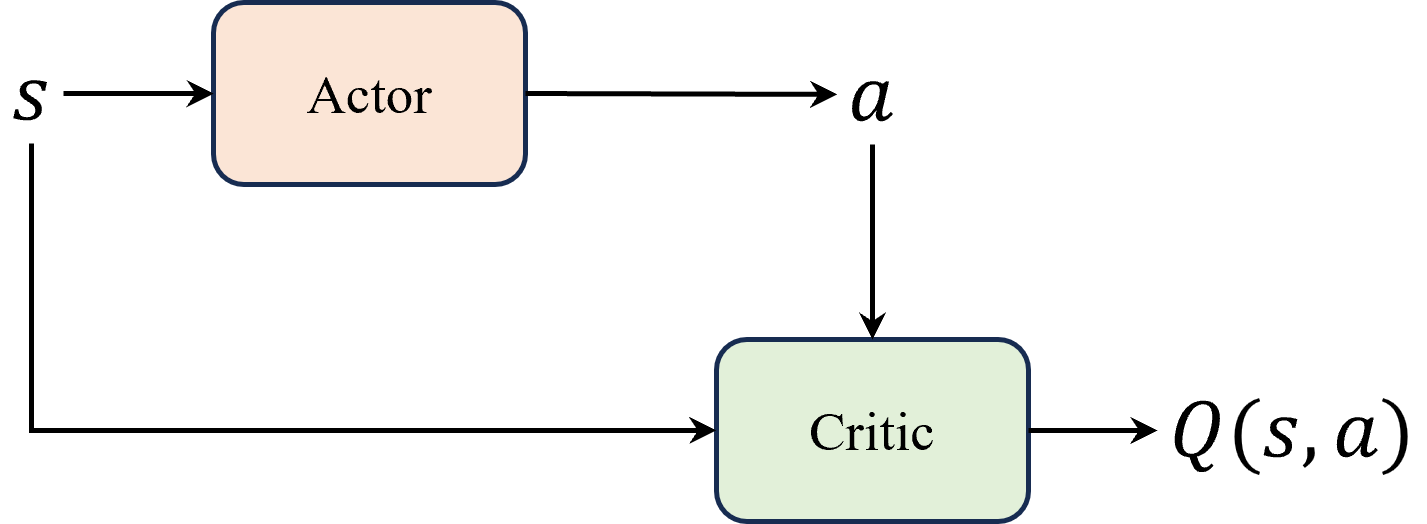
估计Q函数 和贪心选择动作1步求解动作: 直接输出动作值Critic核心思想
神经网络输出确定性动作,适用于连续动作;使用策略网络,单步更新。DDPG=DPG+技巧
两个网络优化
Q_估计 去逼近Q_target,MSEloss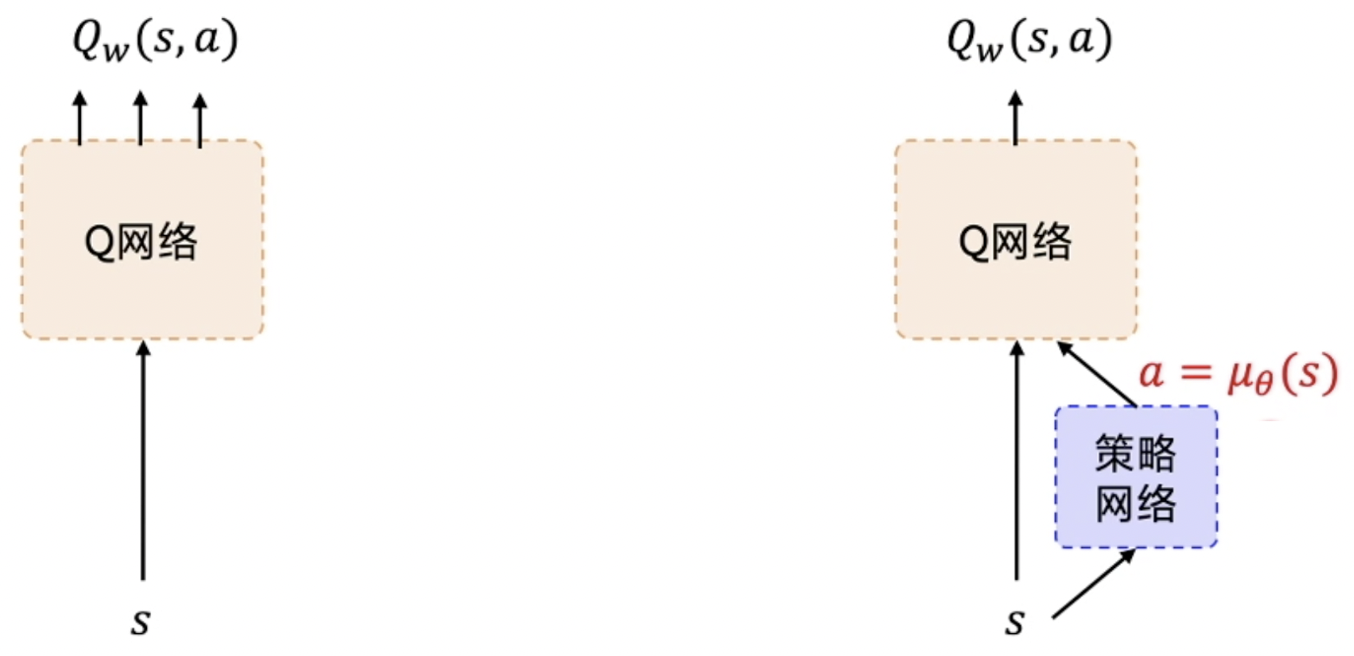
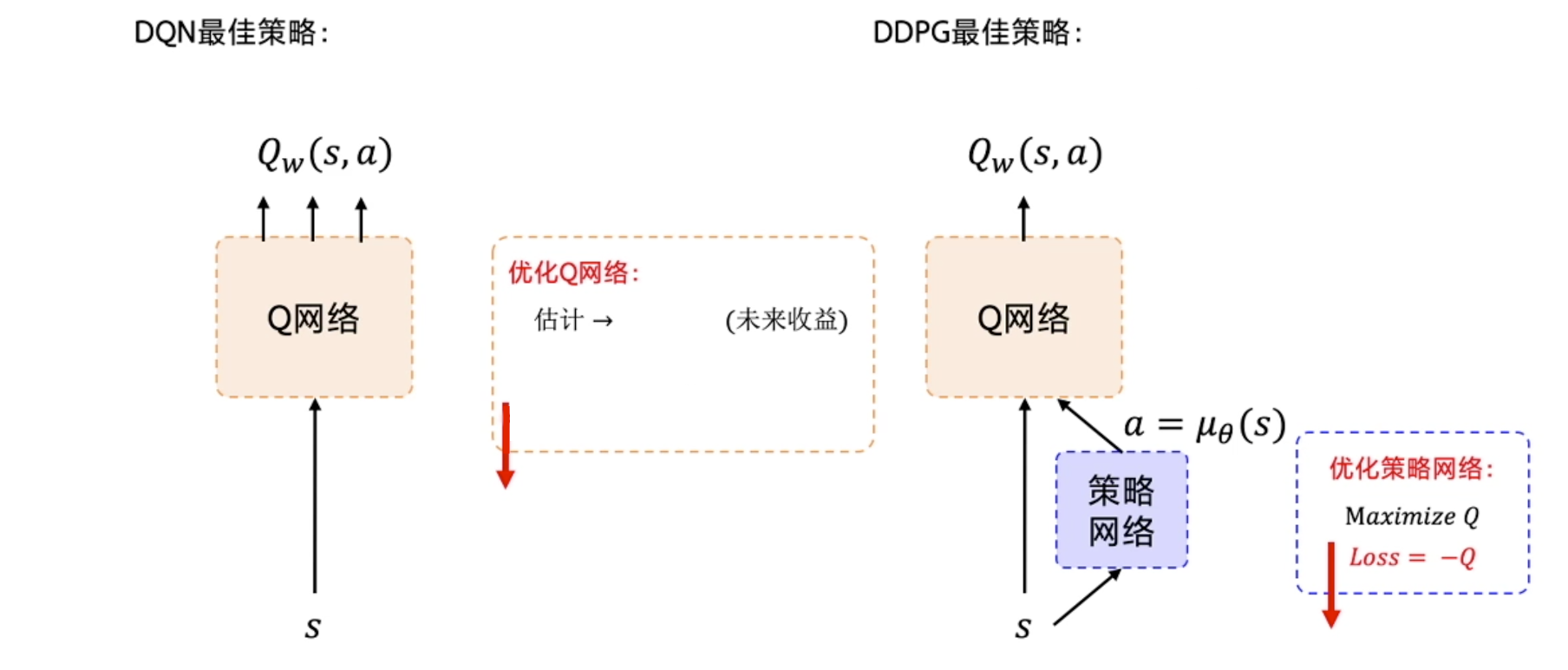
1. 目标网络
2. 经验回放
异策略算法3. OU噪声/高斯噪声
核心思想:策略是直接输出动作,则在输出值上加一个噪声
高斯噪声:不相关、均值为0,简单、效果更好。
OU噪声:自回归随机过程,相比高斯有优点:
定义
相比高斯噪声的优点
优点
缺点
核心思想
双Q网络 vs DoubleDQN
背景
核心思想
优点
降低了领导决策的失误率缺点
没有从根本上考虑改进Critic误差问题,治标不治本背景
核心思想
给Critic输入增加一个噪声,提高抗干扰性,来提高稳定性为噪声加一个裁剪,防止噪声过大