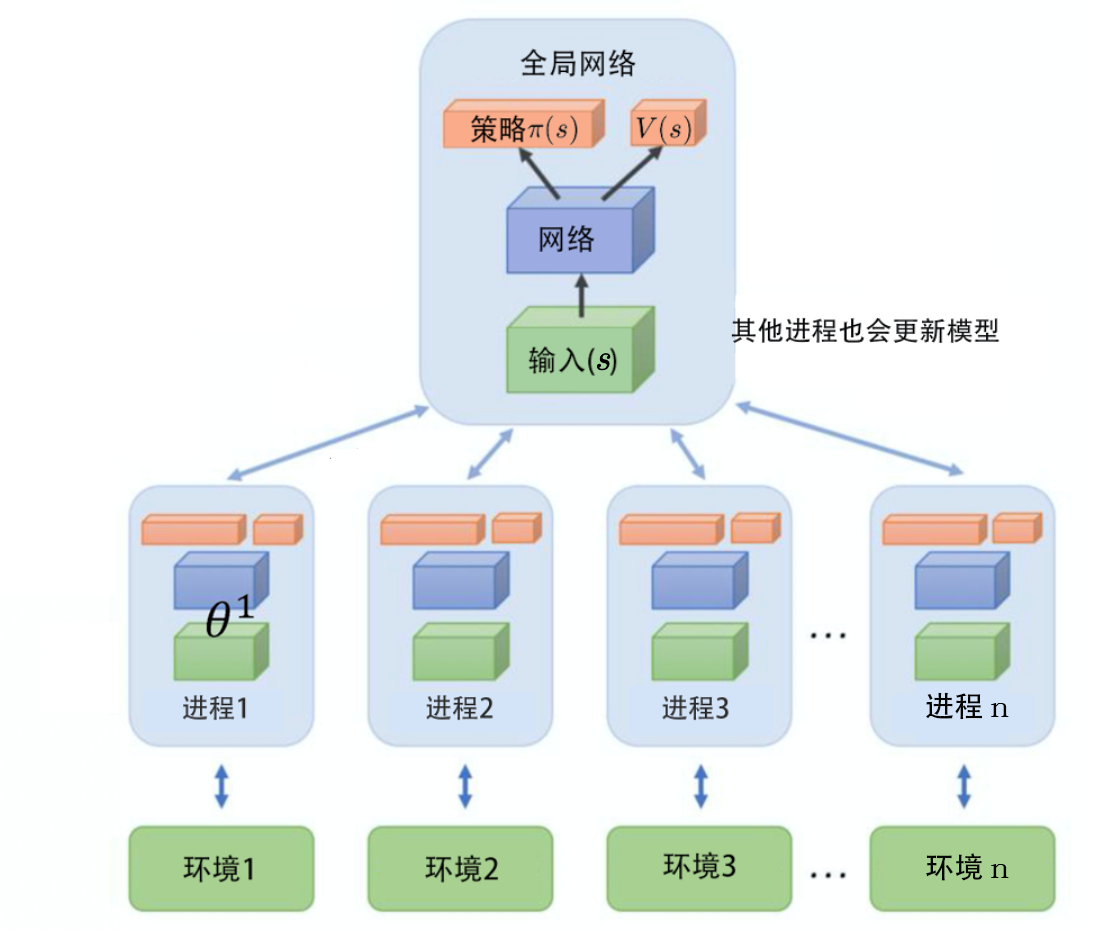
Actor-Critic 算法

Actor-Critic 架构

Actor-Critic

整体流程

• 演员：根据舞台状态做出动作
• 评委：根据舞台状态、演员动作，进行打分 $Q_w(s,a)$
• 演员：根据评委打分调整策略，更新参数$\theta$，争取下次做的更好
• 评委：根据观众反馈/环境反馈，调整打分策略，更新参数$w$，让评的更准

关键点

• 评委目标：让演员表演尽可能获得观众更多掌声，从而最大化未来总收益，评委根据观众评的更准。
• 演员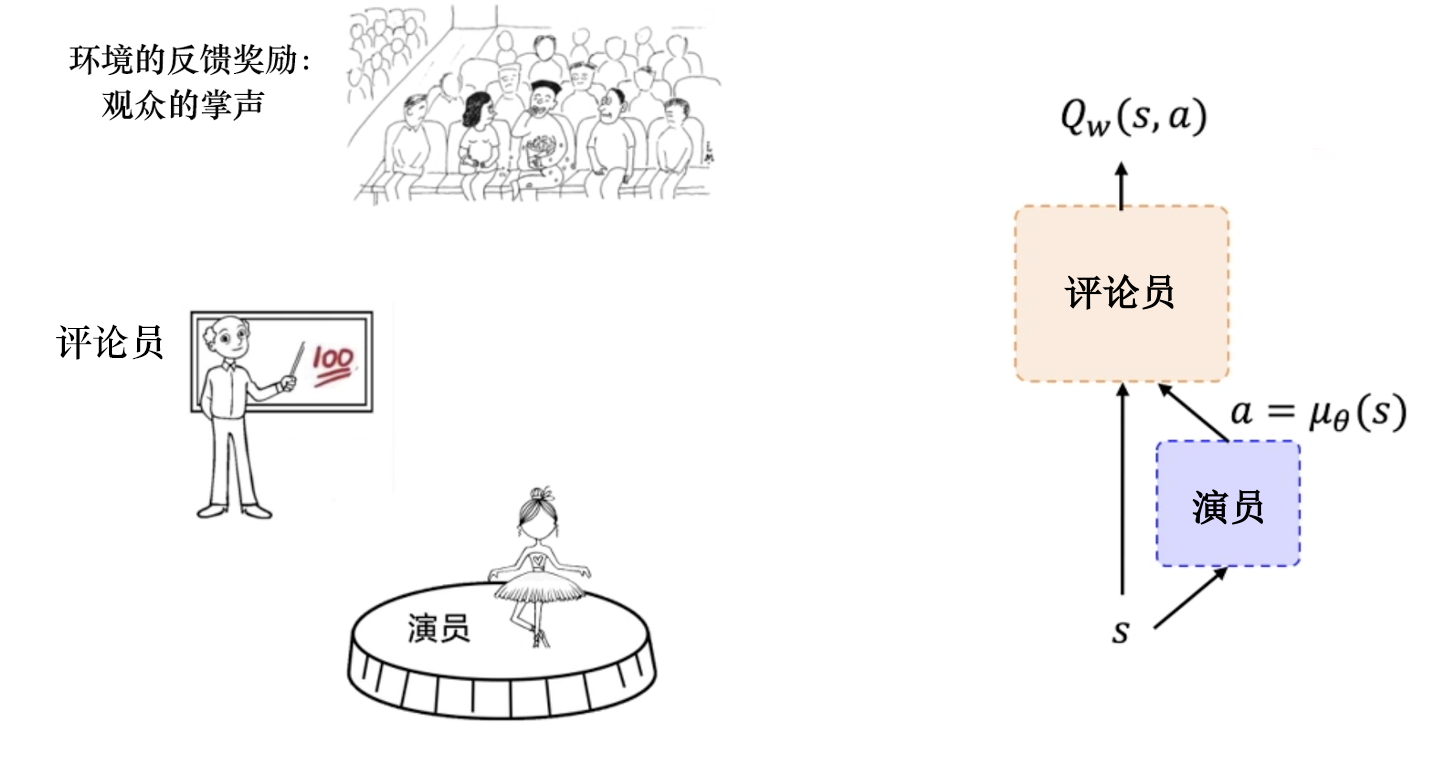：演员不关注观众，演员只迎合评委。

核心思想

Actor-Critic 核心思想

背景

• REINFORCE算法 使用MC采样，存在缺点
  • 需采样完整轨迹回报才能更新价值函数
  • MC采样带来高方差问题(轨迹随机性)：影响收敛速度，且不适合在线学习
• REINFORCE：MC方法。
• Actor-Critic：TD改进版本

核心思想

• 结合基于值函数和基于策略的优点，结合策略梯度和时序差分的强化学习算法。
• Critic网络 评估当前策略好坏，Actor 网络 根据Critic 评估结果来更新策略。

演员&评论员

• 演员：策略${\pi }_{\theta }(a\mid s)$；
  • 目标：根据Critic结果，学习好的策略，尽可能获得高回报。
  • 会和环境交互采样
• 评论员：价值网络 $V_w(s)$、$Q_w(s,a)$
  • 目标：准确评估当前策略的好坏
  • 评估当前$(s,a)$的价值
• 相互博弈思想

优点

• 兼顾策略梯度和时序差分的优点
• 能缓解二者难以解决的高方差问题
  • 策略梯度算法：利用策略和环境交互采样、估计策略梯度
  • 基于价值的算法：需要和环境采样来估计价值函数
• 为何能缓解高方差问题？
  • Actor 只负责策略梯度和采样
  • Critic 只负责策略的价值估计，带来了更稳定的估计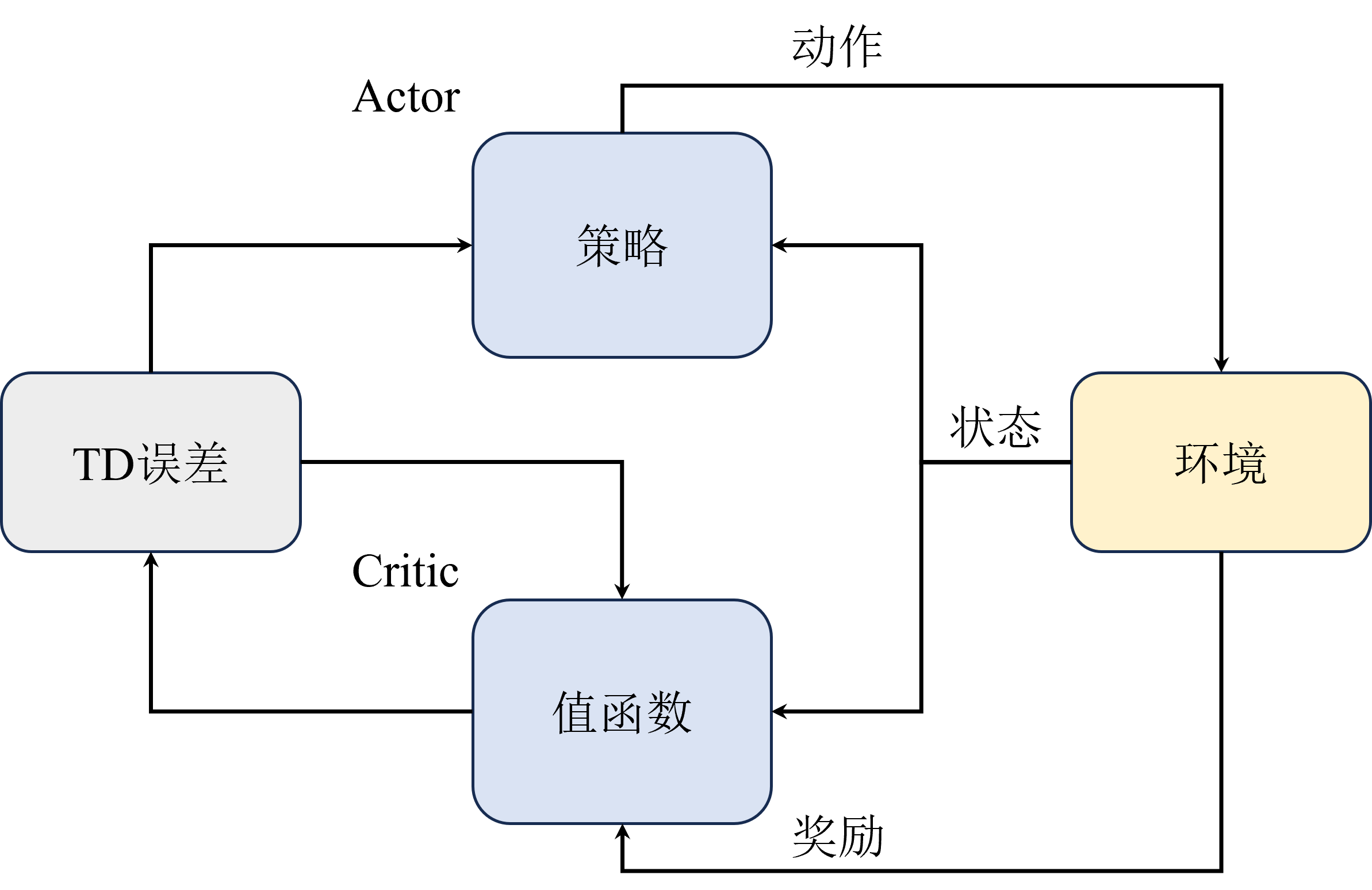

QAC：最简单的AC算法 Q Actor-Critic

Q Actor-Critic

核心思想

• Critic：Q函数$Q_{\varphi }(s_t,a_t)$，作为策略梯度里的权重，代替MC策略梯度里的累计回报$G_t$

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重}}{\underbrace{Q_{\varphi }(s_t,a_t)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

• MC策略梯度使用累计回报$G_t$来作为权重

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重}}{\underbrace{G_t^n}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

参数更新过程

• 策略梯度参数更新过程

$$\theta \leftarrow \theta +\alpha \cdot \mathrm{\nabla }J(\theta )$$

A2C: 优势AC算法 / Advantage Actor Crictic

PG和AC存在的问题

PG和AC存在的问题

朴素PG存在的问题

• 权重$G(\tau )$恒大于0、方差较大
• 一条轨迹内所有动作权重都相同

ActorCritic 存在的问题 (TRPO/PPO来解决)

• 更新步长选择困难症

• 每次梯度更新时，都对策略做采样。

  • 导致训练过程比较慢、采样随机性导致可能朝着错误方向更新。

• TD Error 估计优势函数是有偏的

核心思想

• PG减去基线作为优势函数
• 为轨迹线不同动作分配合适的分数

A2C

背景

• 减去基线作为优势，解决权重$R(\tau )$恒大于0带来的问题
  • 方差大
  • 未采样到的动作，概率被更新(下降)
• 使用优势，解决 轨迹线上所有动作权重都相同的问题

核心思想

• 引入优势函数=Q-V作为权重，动作是Q，基线是V
  • 优势表示当前$(s,a)$相比其他动作平均水平的优势
  • $V_{\pi }(s_t)$ 是同一状态下的基线， 而非所有状态的均值

$$A_{\pi }(s_t,a_t)=Q_{\pi }(s_t,a_t)-V_{\pi }(s_t)$$

• 同策略算法
• 缺点：需要额外引入Q网络，增加了复杂性。

TD Error 作为优势函数

• 避免Q网络，只需V，直接使用 ${\delta }_t$来估计优势函数。虽不精确，但实践效果不错。
  • ${\delta }_t$：当前状态的实际回报和预期回报之间的差值。

$$A_{\pi }(s_t,a_t)={\delta }_t=\underset{TD\mathrm{误}\mathrm{差}}{\underbrace{r_{t+1}+\gamma V_{\pi }(s_{t+1})-V_{\pi }(s_t)}}$$

• 也可以这么理解
  • Q：由V+TD估计得到，去掉了期望值， 因为论文实验其效果好

$$Q_{\pi }(s_t,a_t)=E[r_{t+1}+\gamma V_{\pi }(s_{t+1})]\approx r_{t+1}+\gamma V_{\pi }(s_{t+1})$$

• 请注意：TD Error 估计是有偏的

优点

• 只需估计V，无需估计Q
• r的方差相比G的方差 小很多

策略梯度及Loss函数

策略梯度相关loss

• 朴素PG策略梯度 Loss
• Actor-Critic 策略梯度及Loss
• PPO Critic Loss

优势策略梯度及Loss

策略梯度

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重},\mathrm{优}\mathrm{势}\mathrm{值}}{\underbrace{A_{\pi }(s_t^n,a_t^n)}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重},\mathrm{优}\mathrm{势}\mathrm{值}}{\underbrace{(Q_{\pi }(s_t^n,a_t^n)-V_{\pi }(s_t^n))}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重},\mathrm{优}\mathrm{势}\mathrm{值}}{\underbrace{(r_t^n+\gamma V_{\pi }(s_{t+1}^n)-V_{\pi }(s_t^n))}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

参数更新过程

• 策略梯度参数更新过程

$$\theta \leftarrow \theta +\alpha \cdot \mathrm{\nabla }J(\theta )$$

策略梯度Loss

• Actor Loss
  • 策略梯度 * 权重(优势) ，权重指引优化方向
  • actor_loss = -(log_probs * advantages.detach()).mean()

$$\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}=-A_{\pi }(s_t,a_t)\cdot \log p_{\theta }(s_t,a_t)$$

• Critic Loss
  • 使用TD error 均方误差作为critic loss
    • 目标是使Critc评估得越来越准
    • 使得状态的预期回报接近实际回报。
  • critic_loss = advantages.pow(2).mean()
  • Critic 目标 (理解见下文)

$$\arg \underset{V_{\varphi }}{min}L(V_{\varphi })=E_t[(r_t+\gamma V_{\varphi }(s_{t+1})-V_{\varphi }(s_t){)}^2]$$

优点

• 减去基线，降低了方差，详见降低方差数学推导过程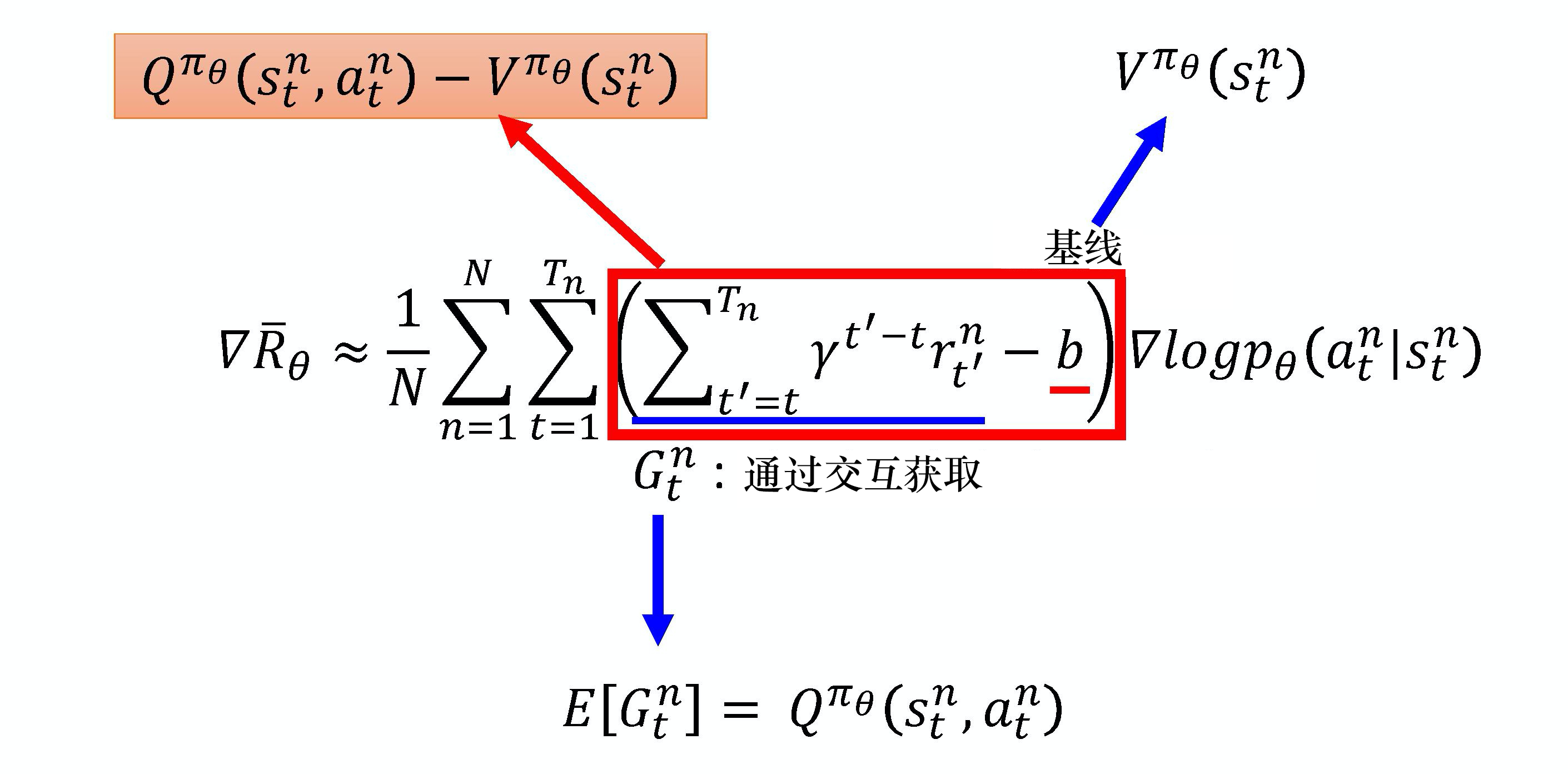

优势及优势趋于0的理解

优势相关笔记

• A2C 优势算法
• A2C 优势及趋于0的理解
• Critic Loss 深入理解
• 策略梯度添加基线
• 策略梯度权重设计
• TD Error 估计优势 方差偏差问题
• 广义优势估计

优势趋于0

优势

• 状态s下，执行某个动作a，比其他动作好了多少，这个差值就是优势。
• 优势更合理地帮助衡量单步价值信号，可替换总回报等，见策略梯度权重多种形式

$$A_{\pi }(s_t,a_t)=Q_{\pi }(s_t,a_t)-V_{\pi }(s_t)$$

• $A_{\pi }(s_t,a_t)$优势越大，说明该动作比其他动作更好，应该提升该动作的概率 。按此方式去更新策略。

优势趋于0的时候

• 假设策略走到$s_t$时，存在最优动作$a_t^{\ast }$ ，此时策略产出该动作的概率已是1或最大。

$$\pi (a_t^{\ast }\mid s_t)=1$$

• 此刻，最优动作概率为1，其余动作概率为0。Q已经接近V，从而 A 趋近于0。

$$V_{\pi }(s_t)=\sum _{a_t\in A}\pi (a_t\mid s_t)\cdot Q_{\pi }(s_t,a_t)\leftrightarrow Q_{\pi }(s_t,a_t^{\ast })$$$$A(s_t,a_t^{\ast })=Q_{\pi }(s_t,a_t^{\ast })-V_{\pi }(s_t)\leftrightarrow 0$$

• 并非所有动作区分不出好坏，而是此时策略已经趋于最优，产出最优$a_t^{\ast }$的概率就是最大的。
• Critic Loss /优势趋于0 的意义
  • 对actor来说，推动它找到某个状态下最佳的动作，逐步向${\pi }^{\ast }$拟合
  • 对critic来说，推动它准确衡量当前策略的价值，逐步向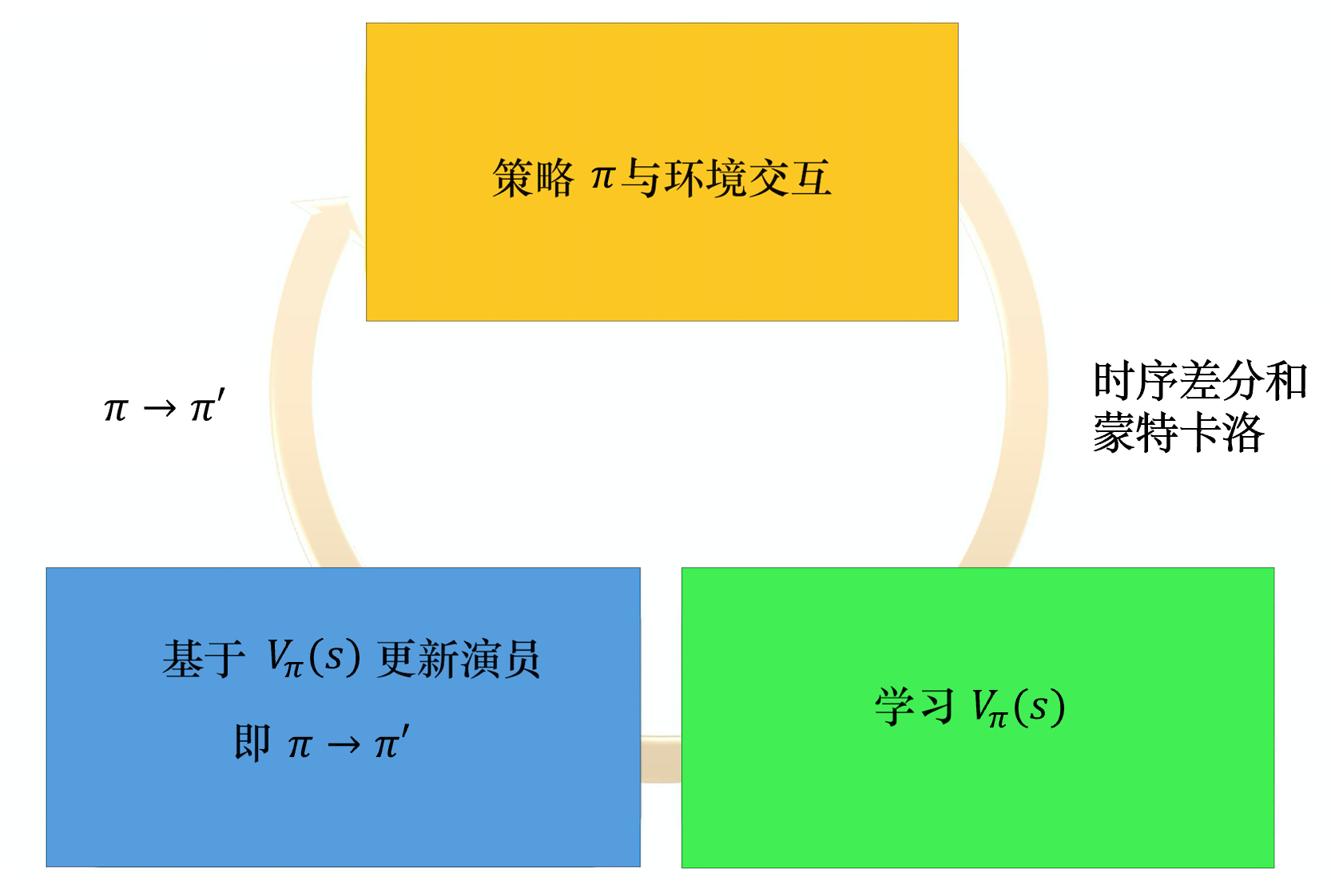$V_{{\pi }^{\ast }}$拟合

TDError 优势偏差和方差问题

TD Error 方差偏差笔记

• TD Error 估计优势 方差偏差问题

算法流程

A2C 算法流程

• 初始Actor(策略$\pi$)，Actor和环境交互，采样一些资料
• 用采样资料结合TD方法，估计V函数
• 基于V函数计算策略梯度，再更新参数

$$\begin{array}{l}\mathrm{\nabla }J(\theta )=\frac{1}{N}\sum _{n=1}^N\sum _{t=0}^{T_n}\underset{\mathrm{权}\mathrm{重},\mathrm{优}\mathrm{势}\mathrm{值}}{\underbrace{(r_t^n+\gamma V_{\pi }(s_{t+1}^n)-V_{\pi }(s_t^n))}}\cdot \underset{\mathrm{动}\mathrm{作}a\mathrm{的}\mathrm{梯}\mathrm{度}}{\underbrace{\mathrm{\nabla }\log p_{\theta }(a_t^n\mid s_t^n)}}\end{array}$$

关键技巧

A2C 关键技巧

1. Stop-Gradient

• 更新Actor时，把Critic参数输出看作常数，避免梯度流向Critic网络。

2：探索机制-熵正则化

• 对$\pi (s)$的输出设置约束，使分布的熵不要太小，希望不同动作的采样概率平均一些
• 避免陷入局部最优

3：优势函数值域固定到[-1,1]

• 做回报归一化，让优势函数更稳定，从而减小反差

4. 共享网络

• 提高训练效率，让Actor和Critic共享一部分参数。

5. 估计V和Actor2个网络

• Critic：$V_{\pi }(s)$，输入状态，输出标量
• Actor：$\pi (s)$，输入状态，输出动作分布，

伪代码

Actor、Critic 定义

# 分开定义
class Critic(nn.Module):
  ''' 估计状态价值，输出标量
  '''
    def __init__(self,state_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, 1)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        value = self.fc3(x)
        return value

class Actor(nn.Module):
  ''' 采样动作，输出logits_p，动作概率
  '''
    def __init__(self, state_dim, action_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.fc3 = nn.Linear(256, action_dim)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        logits_p = F.softmax(self.fc3(x), dim=1)
        return logits_p

# 合在一起定义
class ActorCritic(nn.Module):
  	''' 输入状态，输出动作概率和状态价值
  	'''
    def __init__(self, state_dim, action_dim):
        self.fc1 = nn.Linear(state_dim, 256)
        self.fc2 = nn.Linear(256, 256)
        self.action_layer = nn.Linear(256, action_dim)
        self.value_layer = nn.Linear(256, 1)
    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        logits_p = F.softmax(self.action_layer(x), dim=1)
        value = self.value_layer(x)
        return logits_p, value

Agent：采样动作、计算优势函数、计算loss、策略更新

from torch.distributions import Categorical
class Agent:
    def __init__(self):
        self.model = ActorCritic(state_dim, action_dim)
    
    def sample_action(self,state):
        ''' 动作采样
        '''
        state = torch.tensor(state, device=self.device, dtype=torch.float32)
        # 策略网络输出动作概率分布
        logits_p, value = self.model(state)
        dist = Categorical(logits_p) 
        # 依概率采样一个分布
        action = dist.sample() 
        return action
    
    def _compute_returns(self, rewards, dones):
        ''' 计算回报，做归一化
        '''
        returns = []
        discounted_sum = 0
        for reward, done in zip(reversed(rewards), reversed(dones)):
            if done:
                discounted_sum = 0
            # 折扣回报
            discounted_sum = reward + (self.gamma * discounted_sum)
            returns.insert(0, discounted_sum)
        # 回报归一化
        returns = torch.tensor(returns, device=self.device, dtype=torch.float32).unsqueeze(dim=1)
        returns = (returns - returns.mean()) / (returns.std() + 1e-5) # 1e-5 to avoid division by zero
        return returns
    
    def compute_advantage(self):
        ''' 计算优势
        '''
        # 从经验池中采样数据：动作概率、状态、回报、结束
        logits_p, states, rewards, dones = self.memory.sample()
        # 根据rewards 计算回报
        returns = self._compute_returns(rewards, dones)
        states = torch.tensor(states, device=self.device, dtype=torch.float32)
        # 当前模型去估计状态价值 
        logits_p, values = self.model(states)
        # 实际回报 - 状态价值 作为优势
        advantages = returns - values
        return advantages
      
  	def compute_loss(self):
        '''计算损失函数
        '''
        # 采样数据
        logits_p, states, rewards, dones = self.memory.sample()
        returns = self._compute_returns(rewards, dones)
        states = torch.tensor(states, device=self.device, dtype=torch.float32)
        # 估计价值V、计算策略logits_p
        logits_p, values = self.model(states)
        # 计算advantages
        advantages = returns - values
        dist = Categorical(logits_p)
        # 计算log_prob
        log_probs = dist.log_prob(actions)
        # 注意这里策略损失反向传播时不需要优化优势函数，因此需要将其 detach 掉
        actor_loss = -(log_probs * advantages.detach()).mean() 
        # critic loss
        critic_loss = advantages.pow(2).mean()
        return actor_loss, critic_loss

A3C 异步优势AC算法/ Asynchronous Advantage Actor Critic

A3C：A2C算法的异步扩展版

背景

• 强化学习很慢，需要加快速度
• 可以像鸣人一样使用多个分身进行修行。

核心思想

• 使用1个全局网络+多个worker并行探索训练
• 每个进程单独训练，计算出梯度后回传中央控制中心，去更新原来的参数。
  • 原来的参数被别的进程覆盖掉怎么办？没关系，还是正常更新就好了
• 是一种同策略算法，虽然看起来像异策略
  • 每个worker内，只用当前策略采样的数据计算梯度

优点

• 不存储历史数据，通过平行探索，保持训练稳定性