马尔可夫决策过程
📅 发表于 2025/08/26
🔄 更新于 2025/08/26
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
rl
#马尔可夫性质
#马尔可夫过程
#马尔可夫奖励过程
#奖励
#回报
#价值函数
#折扣因子
#V函数
#Q函数
#贝尔曼方程
#贝尔曼期望方程
#贝尔曼最优方程
#动态规划
#自举
#预测
#策略评估
#控制
#策略搜索
定义
优点
实际情况
状态转移概率:
状态转移矩阵:有限状态的马尔可夫过程
定义
即时奖励
标量反馈信号,智能体到达某状态,获得的即时奖励。回报
未来奖励的逐步叠加是面向未来、无限累计的计算,可通过贝尔曼方程 迭代计算。对未来奖励打折扣,更希望得到现在的奖励平衡当前奖励和未来奖励。 越后面的奖励对当前价值的影响,会越来越小价值
即时奖励+ 未来状态的折扣价值。回报的期望,进入某状态后,可能获得多大的回报回报的期望,在某状态采取某动作,可能获得多大回报V函数的贝尔曼方程
即时奖励+未来奖励的折扣总和。V函数贝尔曼方程的证明过程
推导过程:见下文
关键内容:证明如下公式 + 数学全期望公式 +
状态太多时,不太能直接使用矩阵求逆求解价值函数,一般使用迭代算法来进行求解。包括蒙特卡洛方法,动态规划方法,时序差分方法等。
核心思想
随波逐流产生多条轨迹,每条轨迹算出回报g对多条轨迹的回报g做平均,即得到状态价值核心思想
迭代贝尔曼方程,直到价值函数收敛,得到状态价值。未来的价值估计 来更新 现在的价值估计其他估算值来更新 估算值;用下一个状态的价值来更新当前状态的价值。算法过程
关键定义
当前状态和智能体在当前状态采取的动作奖励函数:由状态和当前动作决定
轨迹
核心思想
策略
随机性策略 或 确定性策略马尔可夫决策过程4元组:
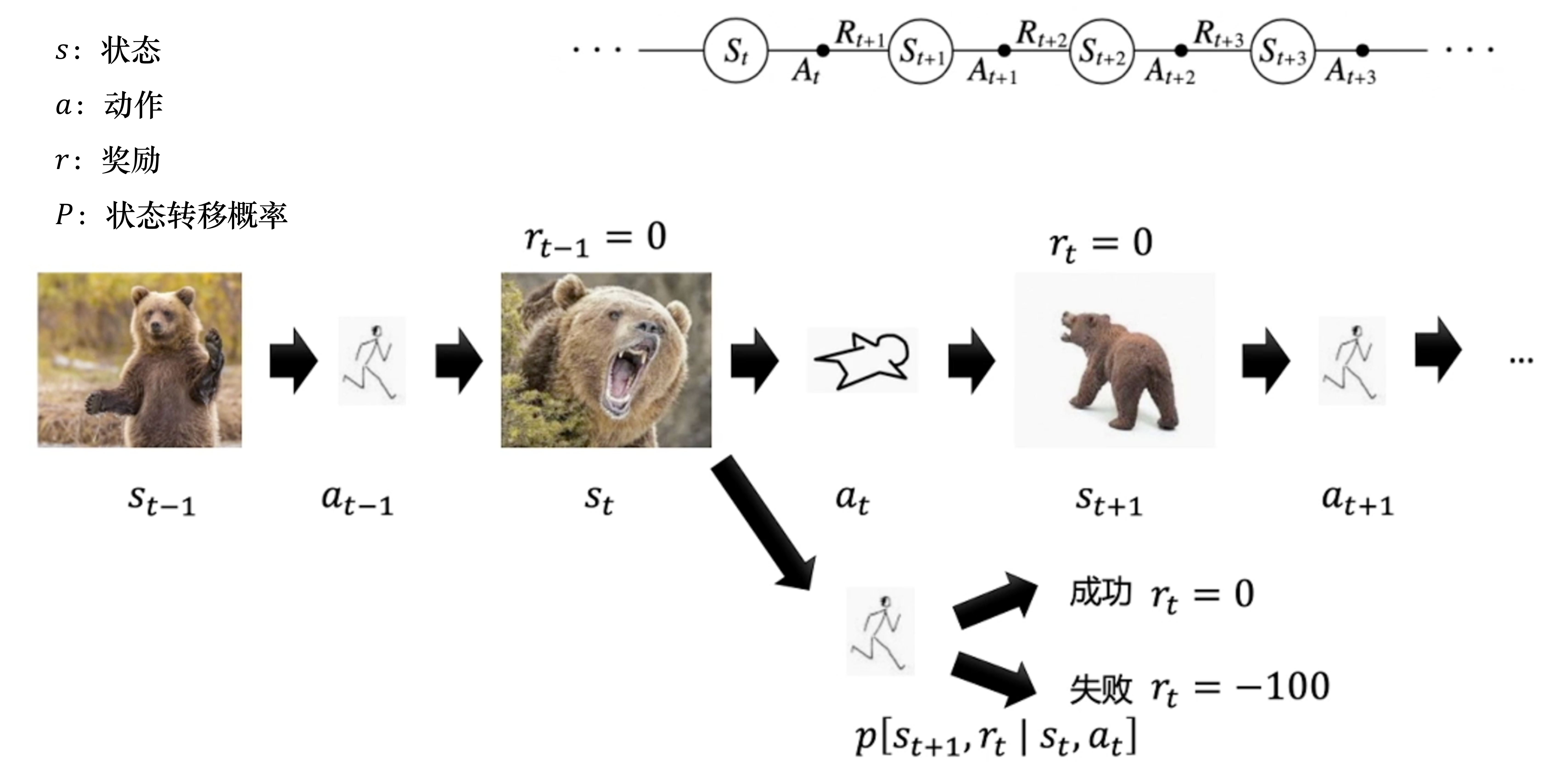
状态转移和序列决策:
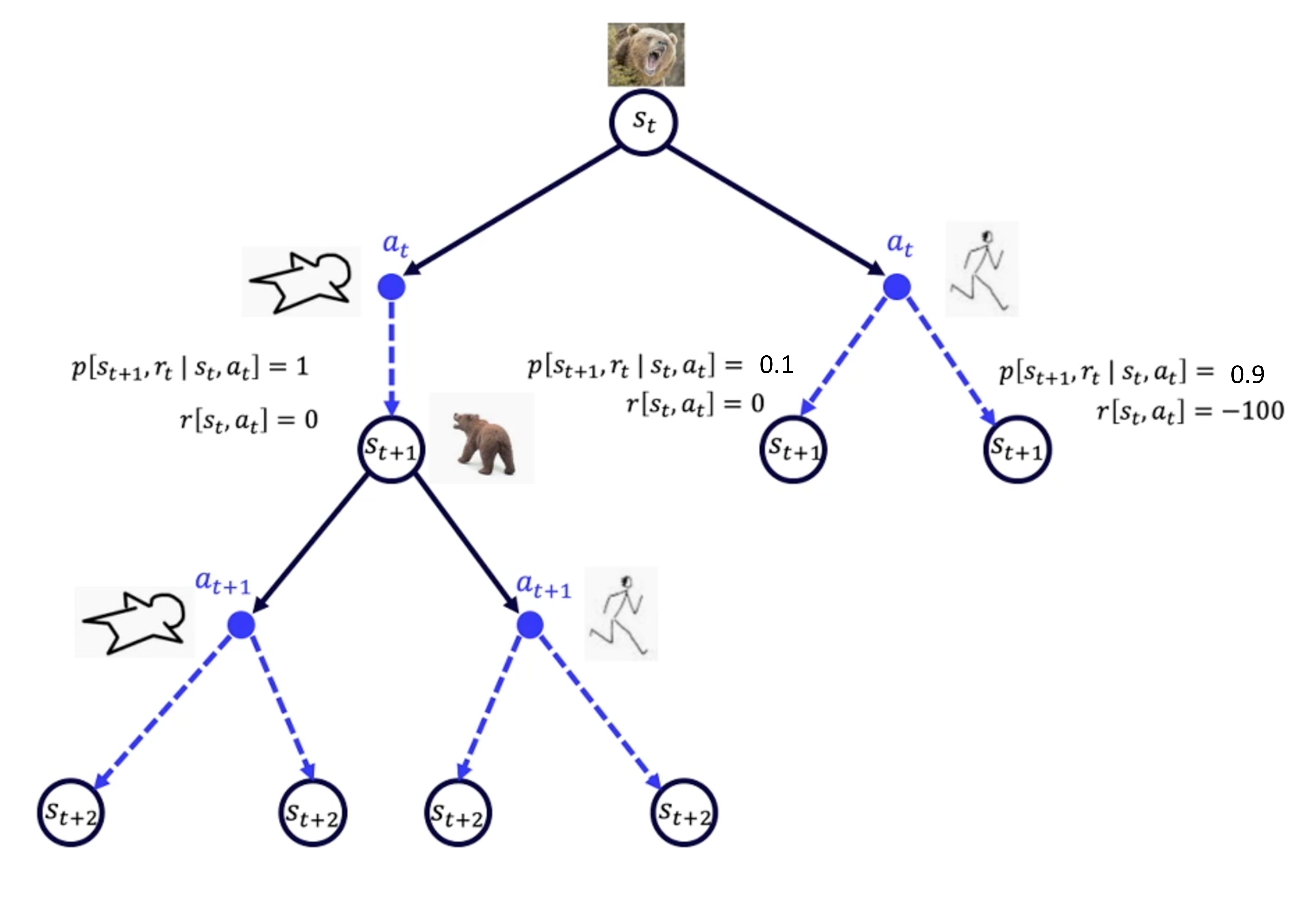
状态转移直接由状态决定的状态转移由状态和当前动作决定的,在当前状态和未来状态间多了一层决策性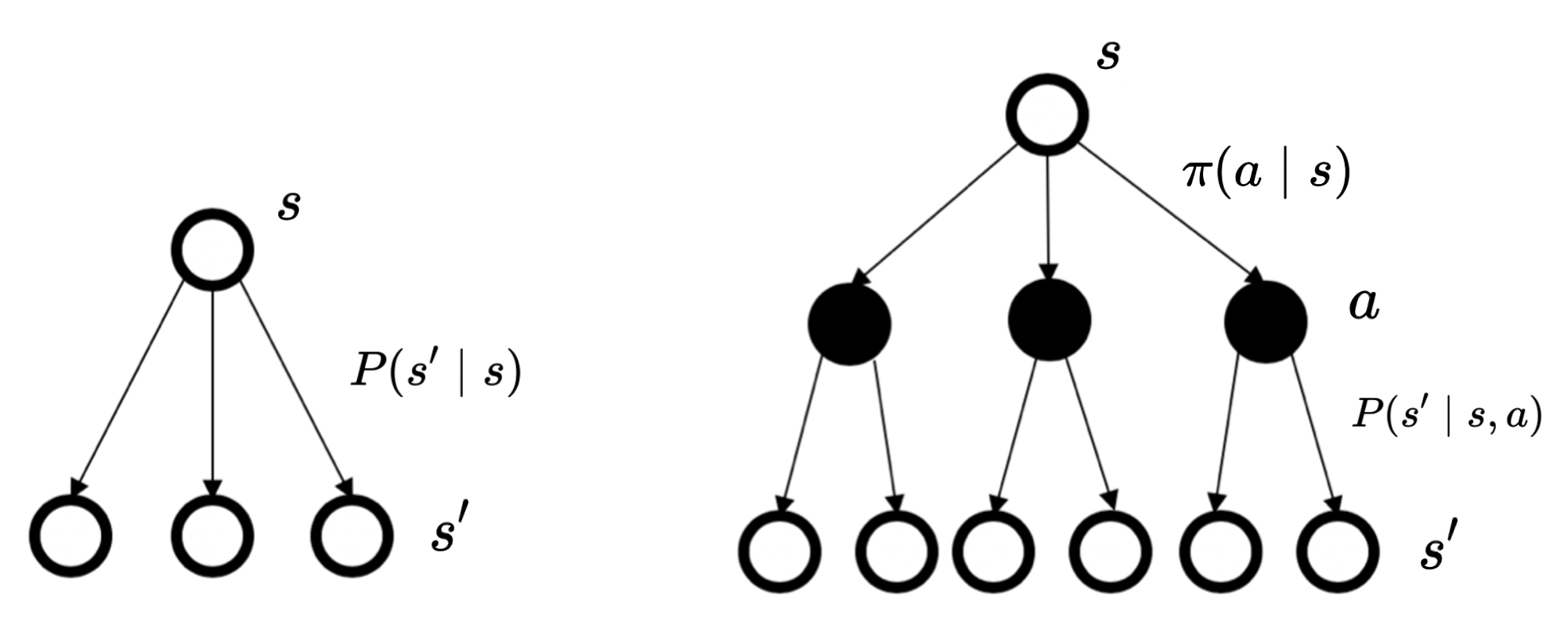

贝尔曼方程奇妙之处就在于,我们把一个无限累加公式,变成了一个有限的递归公式。我们进而可以用迭代的方式,去求解这个状态方程。
状态价值函数/V函数
回报的期望。期望和策略相关动作价值函数/Q函数
回报的期望。贝尔曼期望方程
当前状态和未来状态的关联关系当前即时奖励 + 后续状态的折扣回报。V函数的贝尔曼期望方程
Q函数的贝尔曼期望方程
备份图
1. 基础定义
2. V函数的贝尔曼方程
通过V计算V,V函数的贝尔曼方程,选择所有可能a的均值通过Q计算V,策略动作价值函数来联系。3. V函数的贝尔曼最优方程:直接选择回报最大的a
V函数计算分解
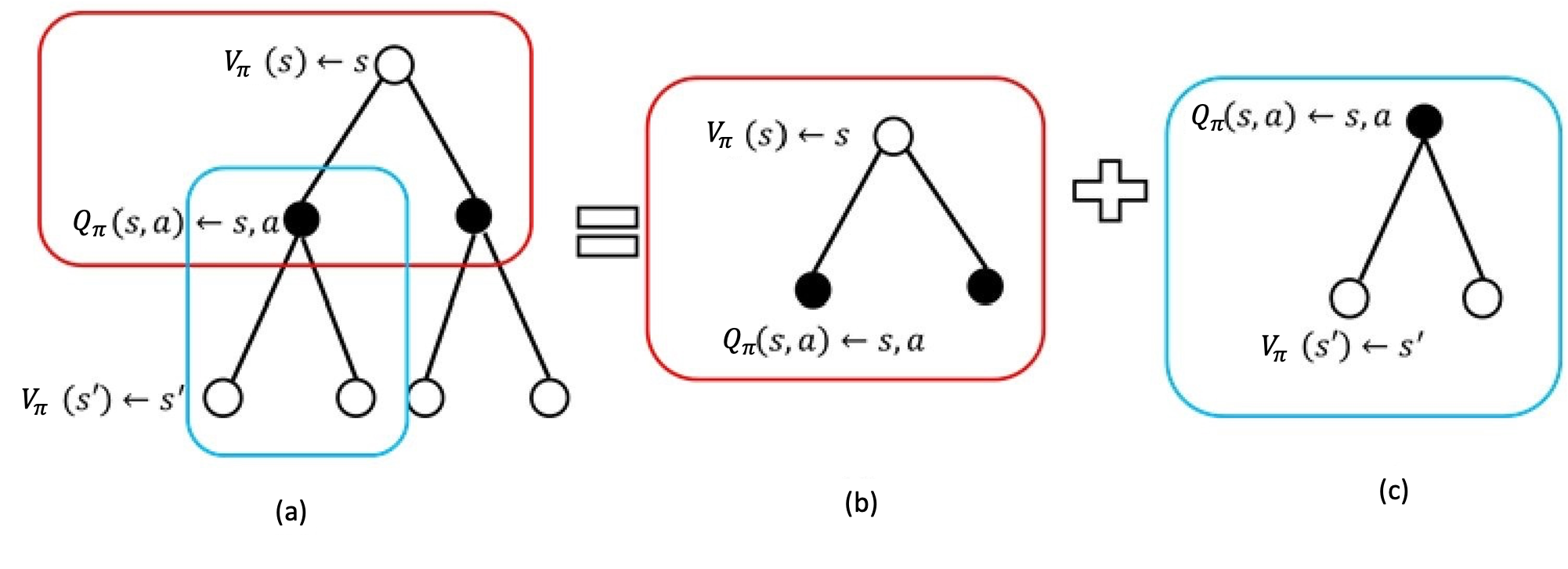
1. Q函数定义:从状态s开始,选择动作a,依照策略
2. Q函数的贝尔曼期望方程
通过V计算Q,Q函数贝尔曼方程,所有可能s的均值通过Q计算Q,Q函数自身迭代计算3. Q函数的贝尔曼最优方程,直接选择最大回报的a
Q函数计算分解
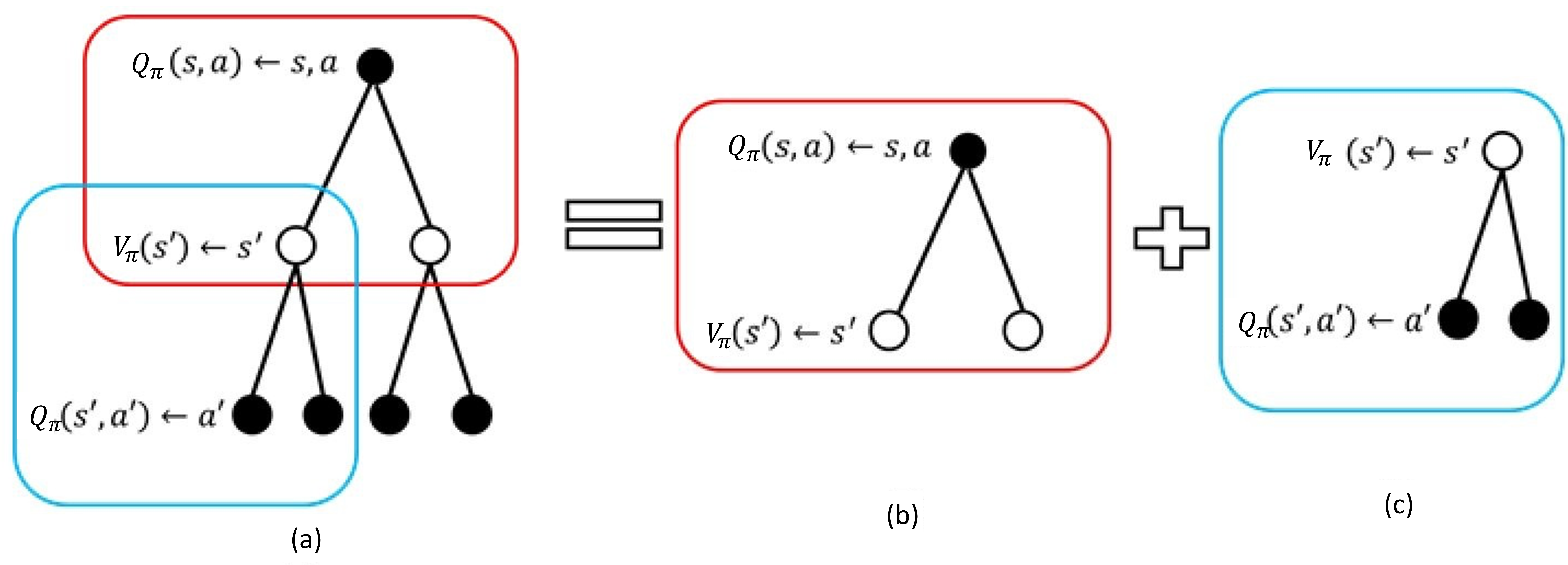
设
贝尔曼方程
即时奖励+未来奖励的折扣总和。V函数贝尔曼方程证明过程
这样也可以
Q函数贝尔曼方程
推导过程
预测/策略评估
控制/寻找最佳策略
预测和控制的关系
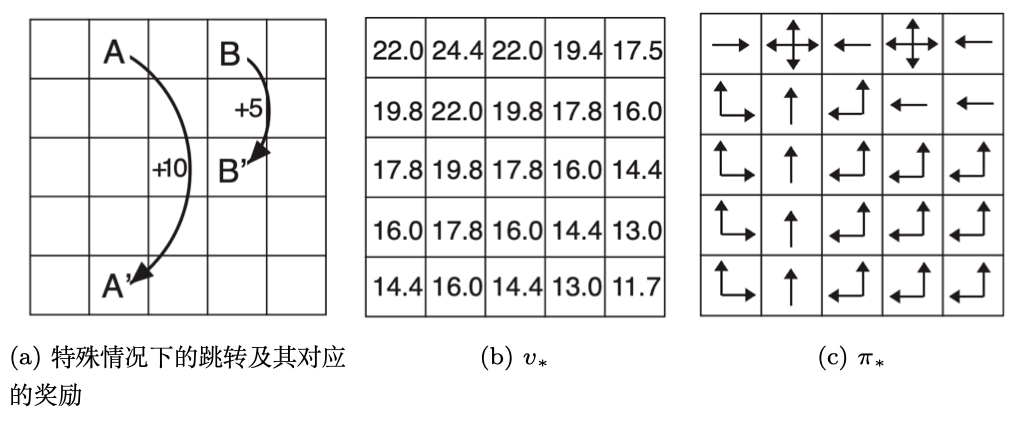
解决控制问题做铺垫。预测:给定策略,等概率上下左右移动,求解价值函数
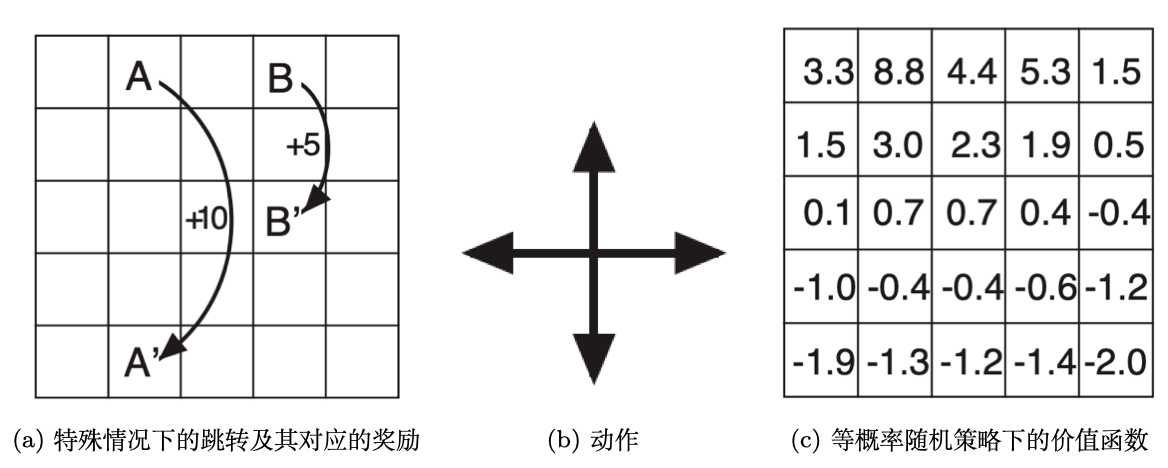
控制:不给定策略,直接求解最优价值,输出对应的策略。