强化学习定义

背景

强化学习

Why RL

• 有监督学习(有标签)+无监督学习(无标签)
  • 从静态数据中学习，学习数据模式 😞
• 强化学习
  • 从动态环境中学习，和环境交互、最大化累计奖励来学习最优策略
  • 状态、动作、奖励 序列是动态的 ⭐
  • RL可做监督学习做不到的事情👍，建模动态的、环境交互的问题。

When RL

• 和环境交互的序列决策问题，能定义出合适的奖励信号
• 无需显示目标函数，只需奖励信号
  • 用优化无法解决的问题，用RL硬Train一发就对了

RL定义

强化学习定义

核心思想🧠

• 智能体🤖和环境交互🌎过程中，根据奖励信号🎁，不断学习调整策略来完成特定目标🏆。
• 其中
  • 无需给出正确策略作为监督信息
  • 只需给出策略的(延迟)回报 ，通过调整策略来取得最大化的期望累计奖励(回报)。

智能体🤖

• 感知环境状态和反馈的奖励，进行决策和学习
• 决策：根据 环境状态 做出不同动作
• 学习：根据 反馈奖励 调整策略

环境🌎

• 智能体外部的所有事物
• 根据智能体动作 改变状态
• 给智能体 反馈奖励🎁

强化学习关键要素

1. 状态$s$, State

• 环境的状态(智能体所处的状态)，状态空间$\mathcal{S}$， 离散/连续

2. 动作$a$, Action

• 智能体可执行的动作，动作空间$\mathcal{A}$， 离散/连续

3. 策略$\pi (a\mid s)$, Policy

• 智能体根据环境状态s决定下一步动作a，分为确定性策略和随机性策略

$$\pi (a\mid s)\triangleq p(a\mid s),\sum _{a\in \mathcal{A}}\pi (a\mid s)=1$$

4. 状态转移概率$p(s\prime \mid s,a)$ 环境模型

• 根据当前状态$s$ 和智能体的动作$a$，环境状态变为$s\prime$的概率

5. 即时奖励$r(s,a,s\prime )$, Reward 环境模型

• 环境根据智能体行为给出的奖励，标量函数。
• 依赖环境当前状态s 、智能体执行动作a、环境新状态$s^{\prime }$
• 注意：也有人简化为$r(s,a)$ 💡，仅依赖当前状态s和执行动作a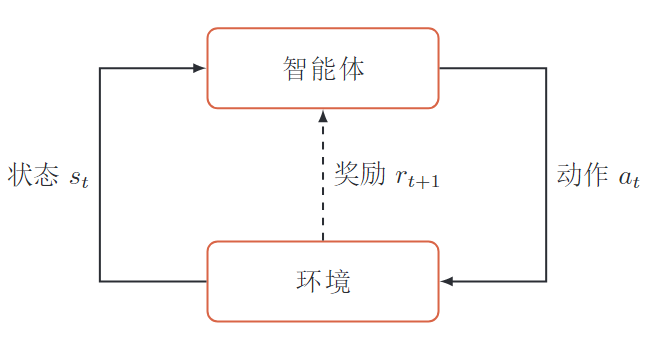

环境交互过程(轨迹)

智能体与环境的交互是一个马尔可夫决策过程。

马尔科夫决策过程

1. 马尔科夫过程 $p(s_{t+1}\mid s_t)$

• 状态序列$s_0,s_1,\cdots ,s_t$具有马尔可夫性，新状态$s_{t+1}$ 只依赖于 当前状态$s_t$

$$p(s_{t+1}\mid s_t,\cdots ,s_0)=p(s_{t+1}\mid s_t)$$

2. 马尔科夫决策过程 $p(s_{t+1}\mid s_t,a_t)$

• 新状态$s_{t+1}$ 依赖于 当前状态$s_t$ 和 智能体当前的动作$a_t$

$$p(s_{t+1}\mid s_t,a_t,\cdots ,s_0,a_0)=p(s_{t+1}\mid s_t,a_t)$$

轨迹

轨迹定义

• 轨迹$\tau$ 是智能体与环境的一次交互过程(马尔可夫决策过程)，给定策略$\pi (a\mid s)$，如下：

$$\tau =s_0,a_0,s_1,r_1,\cdots ,s_{T-1},a_{T-1},s_T,r_T$$

• $r_t=r(s_{t-1},a_{t-1},s_t)$：时刻$t$的即时奖励。

轨迹概率

• 轨迹概率是初始状态的概率 和 所有时刻概率的 乘积
• 每一时刻：智能体执行动作、环境更新状态 💥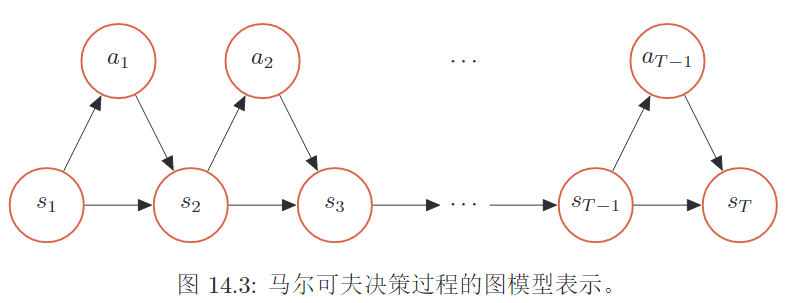

$$p(\tau )=\underset{\mathrm{初}\mathrm{始}\mathrm{概}\mathrm{率}}{\underbrace{p(s_0)}}\prod _{t=0}^{T-1}\underset{\mathrm{执}\mathrm{行}\mathrm{动}\mathrm{作}}{\underbrace{\pi (a_t\mid s_t)}}\cdot \underset{\mathrm{状}\mathrm{态}\mathrm{更}\mathrm{新}}{\underbrace{p(s_{t+1}\mid s_t,a_t)}}$$

强化学习目标

摘要(RL目标)

• 轨迹的总回报：$G(\tau )=\sum _{t=0}^{T-1}{r}_{t+1}$
• 策略的期望回报：$E_{\tau \sim p(\tau )}[G(\tau )]$，所有轨迹回报的期望
• 强化学习的目标：学一个策略${\pi }_{\theta }(a\mid s)$， 最大化这个策略的期望回报

轨迹回报

轨迹总回报

1. 某一时刻的奖励

• $t$时刻，环境给智能体的奖励

$$r_t=r(s_{t-1},a_{t-1},s_t)$$

2. 一条轨迹的回报/总回报

• 一条轨迹所有时刻的累积奖励

$$G(\tau )=\sum _{t=0}^{T-1}r(s_{t-1},a_{t-1},s_t)=\sum _{t=0}^{T-1}{r}_{t+1}$$

3. 一条轨迹的折扣回报

• 引入折扣率 $\gamma$：降低远期回报的权重（T无限大时）

$$G(\tau )=\sum _{t=0}^{T-1}{\gamma }^t\cdot r_{t+1},\gamma \in [0,1]$$

• $\gamma \sim 0$， 在意短期回报
• $\gamma \sim 1$， 在意长期回报

策略的期望回报

策略期望回报

• 一个策略$\pi (a\mid s)$ 有多个轨迹。

• 策略的期望回报：该策略下所有轨迹总回报的期望值。

$$E_{\tau \sim p(\tau )}[G(\tau )]=E_{\tau \sim p(\tau )}\left[\sum _{t=0}^{T-1}{r}_{t+1}\right]$$

强化学习目标

强化学习目标

• 学习到一个策略${\pi }_{\theta }(a\mid s)$，来最大化这个策略的期望回报。希望智能体能获得更多回报。

$$J(\theta )=E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t=0}^{T-1}{\gamma }^t{r}_{t+1}\right]=\int p_{\theta }(\tau )\cdot G(\tau )\mathrm{d}\tau$$

• 基于策略函数的学习方法

  • 本质是策略搜索，优化问题，无需值函数可以直接优化策略

    • 参数化的策略可以处理连续状态和动作，直接学出随机性策略。

  • 方法：基于梯度的优化，无梯度的优化

值函数

摘要

• 状态值函数$V^{\pi }(s)$
  • 初始状态为 $s$ ， 执行策略$\pi$ 得到的期望总回报
• 状态动作值函数$Q^{\pi }(s,a)$
  • 初始状态为 $s$ 、进行动作$a$， 执行策略$\pi$ 得到的期望总回报
• 贝尔曼方程计算V和Q函数
• V函数与Q函数的关系
  • $V^{\pi }(s)=E_{a\sim \pi (a\mid s)}[Q^{\pi }(s,a)]$
• 值函数的作用
  • 评估策略$\pi (a\mid s)$，对好的动作a（$Q^{\pi }(s,a)$大 ），增大其概率 $\pi (a\mid s)$

状态值V函数+贝尔曼方程

状态值V函数

状态值函数$V^{\pi }(s)$：初始状态${\tau }_{s_0}=s$，执行策略 $\pi$ ，所有轨迹的期望回报。

$$V^{\pi }(s)=E_{\tau \sim p(\tau )}[\sum _{t=0}^{T-1}{r}_{t+1}\mid {\tau }_{s_0}=s]$$

贝尔曼方程计算V函数

核心思想 📕

• 当前状态的值函数，可通过下个状态的值函数进行递推计算。
  • $V^{\pi }(s)\sim r(s,a,s\prime )+V^{\pi }(s\prime )$。 有动态规划的意思

迭代计算V函数 ⛳

• 初始状态为 $s$ ，执行策略 $\pi$ ，得到所有轨迹的期望回报
• 对当前时刻奖励+下一时刻V值，求期望即可

$$V^{\pi }(s)=E[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]$$

V函数的贝尔曼方程⭐

• 对执行动作 $s\sim a$、 状态变更 $s,a\sim s^{\prime }$，这2层所有的值函数，求期望即可

$$\begin{array}{ll}{V}^{\pi }(s)& =E_{a\sim \pi (a\mid s)}{E}_{s^{\prime }\sim p(s^{\prime }\mid s,a)}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]\\ & =\sum _{a,s^{\prime }}\pi (a|s)\cdot p(s^{\prime }|s,a)(\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}})\end{array}$$

状态动作值Q函数+贝尔曼方程

状态动作值函数+贝尔曼方程求解

Q函数(状态-动作值函数) 🍎

• 初始状态为 $s$ 、进行动作$a$， 执行策略$\pi$ 得到的期望总回报

$$Q^{\pi }(s,a)=\underset{\mathrm{对}\mathrm{新}\mathrm{状}\mathrm{态}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{s^{\prime }\sim p(s^{\prime }|s,a)}}}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]$$

Q函数的贝尔曼方程 ‼️

• 下一时刻的V(s)函数 用 Q(s,a)函数期望来计算 👏

$$Q^{\pi }(s,a)=\underset{\mathrm{对}\mathrm{新}\mathrm{状}\mathrm{态}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{s^{\prime }\sim p(s^{\prime }|s,a)}}}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{对}\mathrm{下}\mathrm{一}\mathrm{动}\mathrm{作}\mathrm{期}\mathrm{望}\mathrm{用}Q\mathrm{函}\mathrm{数}\mathrm{计}\mathrm{算}(\mathrm{重}\mathrm{要})}{\underbrace{\gamma E_{a\prime \sim \pi (a\prime \mid s\prime )}[Q^{\pi }(s\prime ,a\prime )]}}]$$

VQ贝尔曼最优方程及其关系

V函数和Q函数

1. $V^{\pi }(s)$函数 🚀

• 初始状态为 $s$ ， 执行策略$\pi$ 得到的期望总回报
• 先执行动作$s\sim a$， 再状态转移$s,a\sim s\prime$

$$\begin{array}{ll}{V}^{\pi }(s)& =\underset{\mathrm{按}\mathrm{轨}\mathrm{迹}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{\tau \sim p(\tau )}}}[\sum _{t=0}^{T-1}{r}_{t+1}|{\tau }_{s_0}=s]\\ & =E[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]\\ & =\underset{\mathrm{对}\mathrm{动}\mathrm{作}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{a\sim \pi (a\mid s)}}}\underset{\mathrm{对}\mathrm{新}\mathrm{状}\mathrm{态}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{s^{\prime }\sim p(s^{\prime }\mid s,a)}}}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]\end{array}$$

• V函数的贝尔曼方程，选择所有可能a的均值

$$V^{\pi }(s)=E_{a\sim \pi (a\mid s)}{E}_{s^{\prime }\sim p(s^{\prime }\mid s,a)}[r(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime })]=E_{a\sim \pi (a\mid s)}[Q(s,a)]$$

• V函数的贝尔曼最优方程，直接选择回报最大的a

$$V^{\ast }(s)=\underset{a}{max}{E}_{s^{\prime }\sim p(s^{\prime }\mid s,a)}[r(s,a,s^{\prime })+\gamma V^{\ast }(s^{\prime })]=\underset{a}{max}[Q(s,a)]$$

2. $Q^{\pi }(s,a)$ 函数​ ☄️

• 初始状态为 $s$ 、进行动作$a$， 执行策略$\pi$ 得到的期望总回报
• 动作a已确定，只状态转移$s,a\sim s\prime$

$$\begin{array}{ll}{Q}^{\pi }(s,a)& =\underset{\mathrm{按}\mathrm{轨}\mathrm{迹}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{\tau \sim p(\tau )}}}[\sum _{t=0}^{T-1}{r}_{t+1}|{\tau }_{s_0}=s,{\tau }_{a_0}=a]\\ & =\underset{\mathrm{对}\mathrm{新}\mathrm{状}\mathrm{态}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{s^{\prime }\sim p(s^{\prime }|s,a)}}}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{下}\mathrm{一}\mathrm{时}\mathrm{刻}V\mathrm{值}}{\underbrace{\gamma V^{\pi }(s\prime )}}]\\ & =\underset{\mathrm{对}\mathrm{新}\mathrm{状}\mathrm{态}\mathrm{求}\mathrm{期}\mathrm{望}}{\underbrace{E_{s^{\prime }\sim p(s^{\prime }|s,a)}}}[\underset{\mathrm{当}\mathrm{前}\mathrm{时}\mathrm{刻}\mathrm{奖}\mathrm{励}}{\underbrace{r(s,a,s\prime )}}+\underset{\mathrm{对}\mathrm{下}\mathrm{一}\mathrm{动}\mathrm{作}\mathrm{期}\mathrm{望}\mathrm{用}Q\mathrm{函}\mathrm{数}\mathrm{计}\mathrm{算}(\mathrm{重}\mathrm{要})}{\underbrace{\gamma E_{a\prime \sim \pi (a\prime \mid s\prime )}[Q^{\pi }(s\prime ,a\prime )]}}]\end{array}$$

• Q函数的贝尔曼方程，选择所有可能s的均值

$$Q^{\pi }(s,a)=E_{s^{\prime }\sim p(s^{\prime }|s,a)}[r(s,a,s\prime )+\gamma E_{a\prime \sim \pi (a\prime \mid s\prime )}[Q^{\pi }(s\prime ,a\prime )]]$$

• Q函数的贝尔曼最优方程，直接选择最大回报的a$$Q^{\pi }(s,a)=E_{s^{\prime }\sim p(s^{\prime }|s,a)}[r(s,a,s\prime )+\gamma \underset{a^{\prime }}{max}[Q^{\ast }(s\prime ,a\prime )]]$$

3. V和Q的关系🔥

• V函数 是所有动作a的Q函数的期望
• 通过Q函数计算V函数

$$V^{\pi }(s)=E_{a\sim \pi (a\mid s)}[Q^{\pi }(s,a)]$$

• 通过V函数计算Q函数

$$Q^{\pi }(s,a)=E_{s^{\prime }\sim p(s^{\prime }|s,a)}[r(s,a,s\prime )+\gamma V^{\pi }(s\prime )]$$

值函数的作用

值函数的作用

作用

• 值函数：对策略$\pi (a\mid s)$进行评估。💯

示例

• 在状态s，有一个动作a使得$Q^{\pi }(s,a)>V^{\pi }(s)$

• 说明

  • 在状态s执行动作a，高于s状态所有动作的平均值 👏
  • 执行动作a比当前策略$\pi (a\mid s)$好

• 需要

  • 调整参数使$\pi (a\mid s)$的概率增加 ⬆️

深度强化学习

有些任务的状态和动作非常多，并且是连续的。普通方法很难去计算。

可以使用更复杂的函数（深度神经网络）使智能体来感知更复杂的环境状态，建立更复杂的策略。

深度强化学习

• 强化学习 -- 定义问题和优化目标
• 深度学习 -- 解决状态表示、策略表示等问题