(2505) Clip-Cov/KL-Cov

摘要

• paper: entropy mechanism of rl

• 非常有深度的一篇文章。

• 围绕熵坍塌进行了深入研究

  • 模型性能和熵存在预测关系，熵限制，性能有上限。
  • 熵和协方差有关系。协方差2个变量：对数概率和logit变化程度。
  • 高优势高概率token，协方差大，使得熵坍塌

• 提出Clip-Cov和KL-Cov的方法，精准控制少部分高协方差token。

  • 效果很好。7B提升2pt，32B提升6.4pt。

问题背景

熵坍塌

❓问题背景

策略熵坍塌

RL 核心挑战

• RL需要探索和利用平衡

策略熵的含义

• 探索潜力的一个量化指标，代表动作探索空间的不确定性。

熵坍塌的表现

• 训练开始一些step后，策略熵就急剧下降甚至趋于0。策略变得极其确定。

熵坍塌的危害

• 探索停止，无法探索新路径
• 熵耗尽，性能达瓶颈，再继续训练也是徒劳的。

普通正则熵无效

• 简单应用熵正则是无效的。

需要打破熵瓶颈

• 可扩展RL，需要打破熵瓶颈。

熵正则及其问题(无效方法)

熵正则及其问题

Entropy Loss：在loss上减去熵

• 熵越大， loss会小一点。激励模型去寻找熵更高的策略。
  • $\alpha$：entropy_coef

$$L_{\text{entropy}}=L-\alpha \cdot \mathcal{H}({\pi }_{\theta })$$

• 缺点：参数非常敏感，非常脆弱
  • entropy_coef 太小：[0.0001, 0.001]，对熵几乎没有作用，熵依然崩溃
  • entropy_coef 太大：0.01，熵直接爆炸了，胡言乱语，输出随机token

KL Loss：在loss上增加KL惩罚

• 偏离参考模型较远时，loss会大一点。
  • 不希望偏离参考模型太远。通常${\pi }_{ref}$具有较高的熵。确实能起到拉住熵的作用。
  • $\beta$：kl_coef

$$L_{\text{KL}}=L+\beta \cdot D_{\text{KL}}({\pi }_{\theta }||{\pi }_{ref})$$

• 优点：
  • 只要$\beta >0$，确实能稳住熵。$\beta$越大，熵稳定的水平就越高。
• 缺点
  • 扼杀了模型的学习能力。kl_coef>0 模型性能低于kl_coef=0

RL 范式

RL 范式

RL 优化目标

• 优化策略，最大化累计奖励$$\underset{\theta }{max}J(\theta )=E_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(x)}[r(y)]$$

通过策略梯度来优化

• 策略梯度算法

$${\mathrm{\nabla }}_{\theta }J(\theta )=E_{x\sim \mathcal{D},y\sim {\pi }_{\theta }(x)}[\sum _{t=0}^T{A}_t\cdot {\mathrm{\nabla }}_{\theta }\log {\pi }_{\theta }(y_t\mid y_{<t})]$$

PPO 近端策略优化

• PPO 算法：off-policy提高训练、限制策略更新幅度

$$J_{\mathrm{P}\mathrm{P}\mathrm{O}}^{\mathrm{C}\mathrm{L}\mathrm{I}\mathrm{P}}({\pi }_{\theta })=E_{q,o\sim {\pi }_{{\theta }_{old}}}\frac{1}{|o|}\sum _{t=1}^{|o|}min(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})}\cdot A_t,\mathrm{clip}(\frac{{\pi }_{\theta }(o_t\mid q,o_{<t})}{{\pi }_{{\theta }_{old}}(o_t\mid q,o_{<t})},1-ϵ,1+ϵ)\cdot A_t)$$

GRPO 组内优势减小方差

• GRPO 算法：使用组内优势，减小方差$${\hat{A}}_{i,t}={\hat{A}}_i={\hat{r}}_i=\frac{r_i-\text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}$$

策略熵

策略熵定义

策略熵

• 含义：量化不确定性，策略在选择动作时的可预测性、随机性。

• 计算：给定策略和数据，平均token-level的熵，作为策略熵。

  $$\mathcal{H}({\pi }_{\theta },\mathcal{D})=-E_{\mathcal{D},{\pi }_{\theta }}[\log {\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t})]=-\frac{1}{|\mathcal{D}|}\sum _{x\in \mathcal{D}}\frac{1}{|\mathit{y}|}\sum _{i=1}^{|\mathit{y}|}{E}_{y_t\sim {\pi }_{\theta }}[\log {\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t},x)]$$

$$\mathcal{H}({\pi }_{\theta },\mathcal{D})=-\frac{1}{|\mathcal{D}|}\sum _{x\in \mathcal{D}}\frac{1}{|\mathit{y}|}\sum _{i=1}^{|\mathit{y}|}{E}_{y_t\sim {\pi }_{\theta }}[\log {\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t},x)]$$

策略熵公式理解

• ${\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t},x)$

  • 给定输入x和已有y，生成下一词$y_t$的概率，[0, 1]之间，模型自信程度。
  • 值越大，概率越大， 越自信，不确定性越低。

• $\log {\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t},x)$

  • 取对数，$(-\mathrm{\infty },0]$ 之间，值越大，概率越大，越自信，不确定性越低。

• $\frac{1}{|\mathit{y}|}\sum _{i=1}^{|\mathit{y}|}$

  • 序列内部所有token求平均，平均token熵

• $\frac{1}{|\mathcal{D}|}\sum _{x\in \mathcal{D}}$

  • 序列间 所有序列求平均，作为策略熵。概率越大，不确定性越低。

• $-\frac{1}{|\mathcal{D}|}\sum _{x\in \mathcal{D}}$

  • 增加负号，把值转换成正数。
  • 值越小，熵越小，概率越高，不确定性越低；值越大，熵越高，概率越低，不确定性越高。
  $$\mathcal{H}({\pi }_{\theta },\mathcal{D})=-\underset{\mathrm{序}\mathrm{列}\mathrm{间}\mathrm{求}\mathrm{平}\mathrm{均}}{\underbrace{\frac{1}{|\mathcal{D}|}\sum _{x\in \mathcal{D}}}}\underset{\mathrm{内}\mathrm{部}\mathrm{求}\mathrm{平}\mathrm{均}}{\underbrace{\frac{1}{|\mathit{y}|}\sum _{i=1}^{|\mathit{y}|}}}{E}_{y_t\sim {\pi }_{\theta }}[\underset{\text{log probs}}{\underbrace{\log {\pi }_{\theta }(y_t\mid {\mathit{y}}_{<t},x)}}]$$

模型性能和熵

性能和熵关系公式

模型性能和熵存在预测关系

性能和熵直接挂钩

• 在没有熵loss或KL正则的情况下

• 模型性能$R$ 和 策略熵$H$ 之间，存在一个可预测的指数关系

  $$R=-a\exp \mathcal{H}+b$$
  • 系数a、b：反应了策略和数据的内在特征

• 性能提升，熵必然减小。牺牲熵、来提升模型性能。

• 性能和熵挂钩，而不是和计算资源挂钩，且和算法无关，后期实验有验证。

性能存在上限

• 上限：$H=0\to e^H=1$，后续投入再多计算资源也无用

$$R_{\text{max}}=-a+b$$

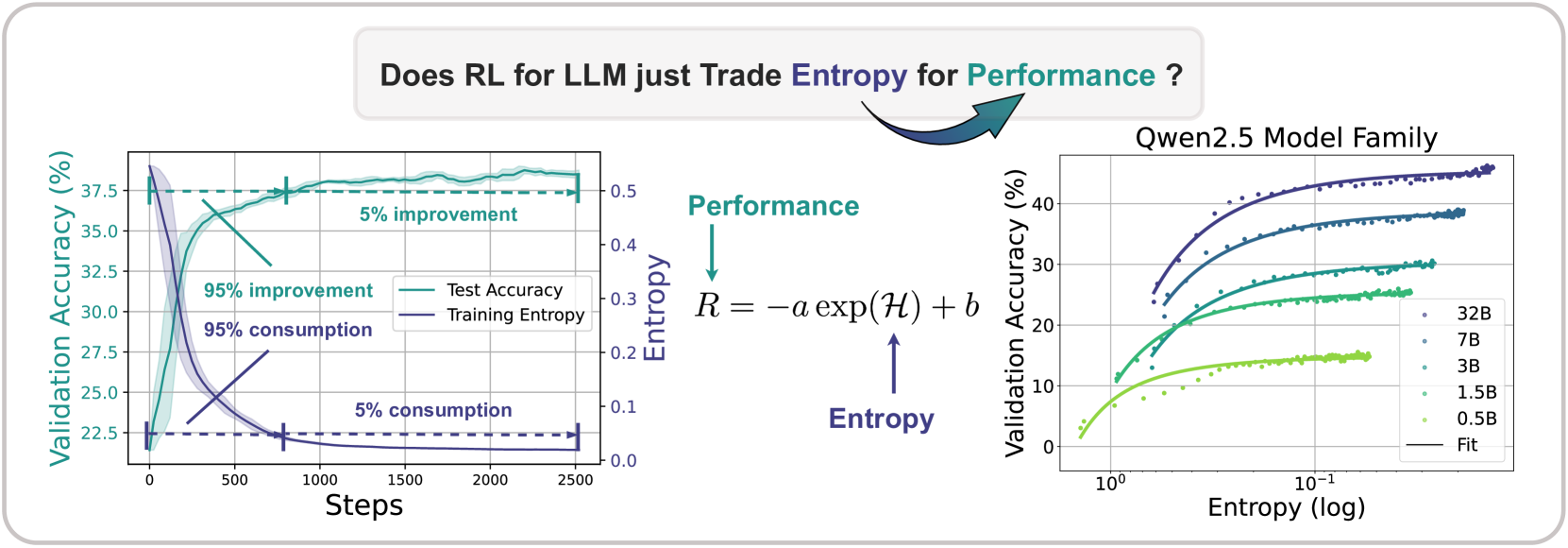
验证实验配置

✍️实验设置

验证实验配置

模型

• Qwen 系列：Qwen2.5 0.5-32B
• Mistral 系列：7B、24B
• LLaMA 系列：LLaMA3.2 3B、LLaMA3.1 8B
• DeepSeek系列：DeepSeek-Math-7B-Base

任务/数据

• 数学
  • 训练：
  • 评测：MATH500, AIME24, AMC, OlympiadBench, OMINI-MATH
• 代码
  • 训练：
  • 评测：Eurus-2-RL-Code, KodCode

算法

• GRPO、REINFORCE++、PRIME

超参

• Lr：5e-7；1e-6 PRM
• bs=256, micro_bs=128
• KL系数：0
• $ϵ=0.2$
• 策略：过滤掉全对或全错的prompt, DAPO 动态采样

验证实验结果

🍑关键结果

11个RL训练实验

早期消耗熵活动性能

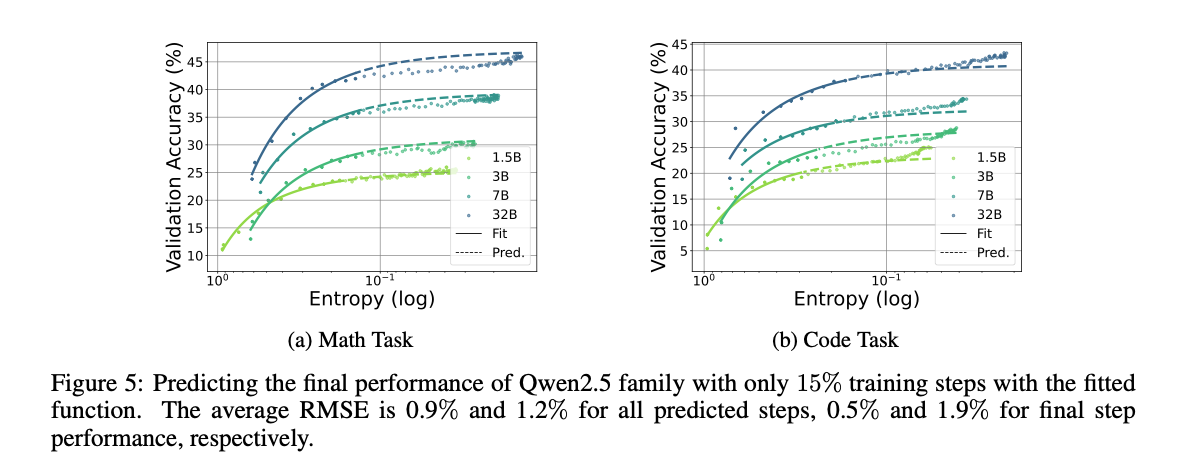
• 前200step(1/12训练)：熵下降73%，性能增益76%。
• 前800step (1/3训练)：熵损失94%，性能增益93%。
• 超过2/3的训练，仅产生很小的回报。

多组实验完美拟合熵和性能的曲线

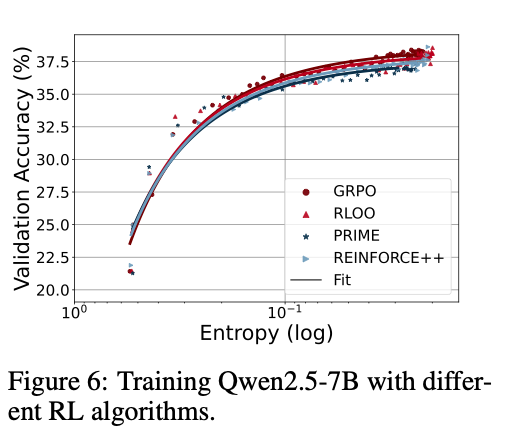
• GRPO 实验。
• 曲线和算法无关，RLOO、PRIME、REINFORCE++都差不多。

ab 系数理解

• a：转化效率。

  • a越大，越擅长把探索潜力转换成性能，越高效，a越大。
  $$\frac{dR}{d\mathcal{H}}=-a\exp \mathcal{H}$$

• b、-a+b：性能潜力

  • 模型越强，$-a+b$ 越大。

早期消耗熵、增加性能。

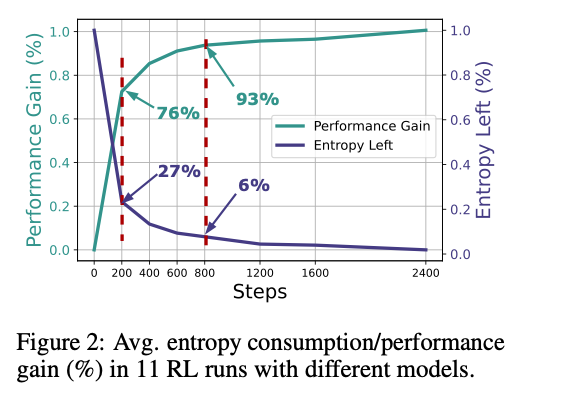
完美拟合曲线：实线是公式计算的，散点是实际测量的(熵, 性能)数据对。

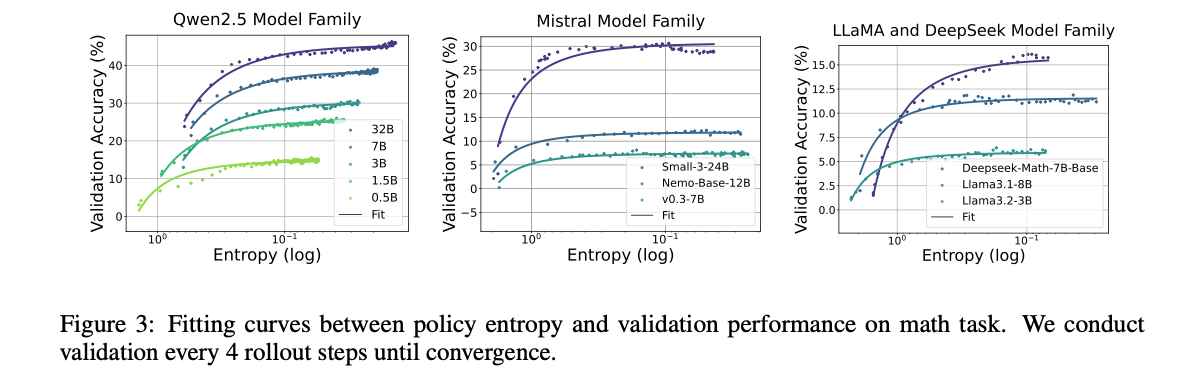
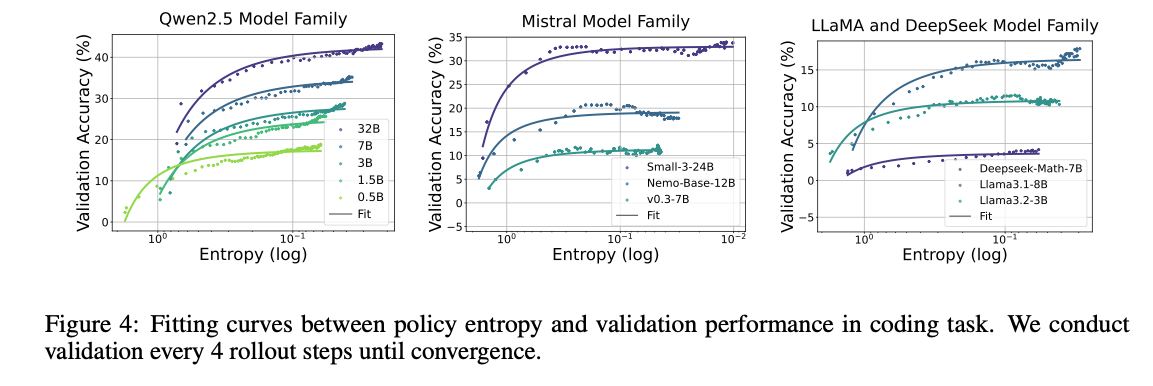
在训练早期，可以通过公式来预测后期性能，性能上限是注定的。

熵性能曲线和RL算法无关，不同算法结果类似。

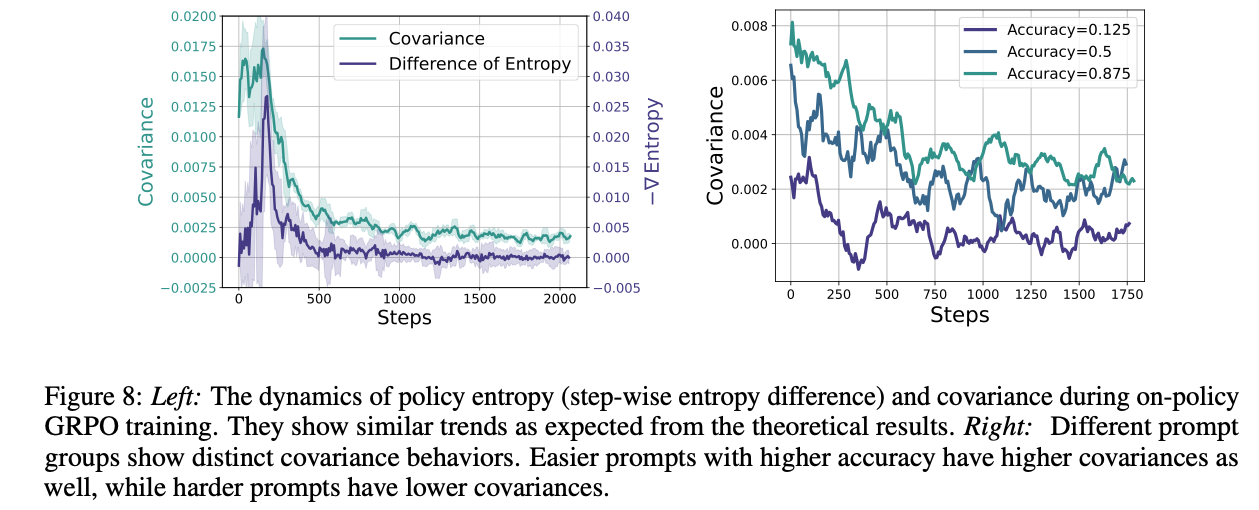
熵和协方差

熵和协方差的关系

熵和协方差有关系

熵变化和协方差有关系

• LLM Softmax这种策略，在两个连续步骤之间
• 熵变化与协方差 有关系。

协方差理解

• 协方差变量：动作的对数概率和对应的logit变化
  • 对数概率/自信程度：生成某个词的概率，值越大，模型越确定
  • logit变化/信念增强程度：模型得到奖励BP后，对这个动作的增强程度。
    • 变化越大：模型认为这个动作越值得被强化
• 当自信程度和信念增强程度同时很高时，协方差为正、很大。
  • 模型继续强化这个动作，排除掉其他可能性，导致熵急剧下降。

高协方差有害

• 高协方差 导致了熵急剧下降，对ScaleRL非常有害。

熵的Token变化关系

• 高优势高概率 Token：协方差大，降低熵

• 高优势低概率 Token：协方差低，增加熵

熵和协方差公式分析及结论

熵和协方差关系 公式推导

Softmax 动作a概率

• $z_{s,a}$：给定状态s，选择动作a的logit

$${\pi }_{\theta }(a\mid s)=\frac{\exp (z_{s,a})}{\sum _{a^{\prime }\in A}\exp (z_{s,a^{\prime }})}$$

熵变化

• 熵变化≈对数概率和logits变化之间的负协方差。

$${\mathrm{\Delta }}_H=H({\pi }_{\theta }^{k+1})-H({\pi }_{\theta }^k)\approx E_{s\sim d_{{\pi }_{\theta }}}[-{\text{Cov}}_{a\sim {\pi }_{\theta }^k(\cdot \mid s)}(\underset{\mathrm{初}\mathrm{始}\mathrm{信}\mathrm{心}}{\underbrace{\log {\pi }_{\theta }^k(a\mid s)}},\underset{\mathrm{变}\mathrm{化}\mathrm{量}}{\underbrace{z_{s,a}^{k+1}-z_{s,a}^k}})]$$$$H({\pi }_{\theta }^{k+1})=H({\pi }_{\theta }^k)+{\mathrm{\Delta }}_H$$

• $\log {\pi }_{\theta }^k(a\mid s)$
  • 在更新前对动作a的初始信息
  • 负对数概率，范围[0, 1]，概率越大，确定性越大，随机性越小。
• $z_{s,a}^{k+1}-z_{s,a}^k$
  • 动作a的logit在更新后的变化量，对a信息的增强或减弱。
• $-{\text{Cov}}_{a\sim {\pi }_{\theta }^k(\cdot \mid s)}(\log {\pi }_{\theta }^k(a\mid s),z_{s,a}^{k+1}-z_{s,a}^k)$​
  • 增加负号
    • 协方差若为正，${\mathrm{\Delta }}_H<0$，熵减小，不确定性变小
    • 协方差若为负，${\mathrm{\Delta }}_H>0$，熵变大， 不确定性变大

协方差结论

结论

• 高概率、高优势 token，导致高协方差，会降低熵。
• 协方差越高、熵下降越快。
• 动作概率和动作优势呈强烈正相关，是导致策略熵下降的根本原因。

实验结论

• 协方差和$-{\mathrm{\Delta }}_H$熵变化趋势一致，协方差越高、熵下降越快。
• 难度大的样本，协方差更低，有助于熵；难度低的样本，协方差高。

• 下图左侧：协方差和$-{\mathrm{\Delta }}_H$ 负熵变化趋势一致
• 下图右侧：难样本，协方差低，有助于熵

两种策略梯度的熵变化公式

两种策略梯度熵变化公式

普通策略梯度

• logit会被当前动作的概率 缩放

$${\theta }_{k+1}={\theta }_k+\eta {\mathrm{\nabla }}_{\theta }J({\theta }_k)$$$$z_{s,a}^{k+1}-z_{s,a}^k=\eta \cdot {\pi }_{\theta }(a\mid s)\cdot A(s,a)$$

• 熵变化

$$H({\pi }_{\theta }^{k+1})-H({\pi }_{\theta }^k)\approx -\eta \cdot {\text{Cov}}_{a\sim {\pi }_{\theta }^k(\cdot \mid s)}(\log {\pi }_{\theta }^k(a\mid s),{\pi }_{\theta }(a\mid s)\cdot A(s,a))$$

自然策略梯度

• 利用fisher信息矩阵的逆矩阵$F^{-1}$对梯度做了预处理。
  • 费雪信息矩阵：衡量参数变化时，策略分布会变化多少。乘以逆矩阵，矫正了参数空间的扭曲。
• NPG
  • 直接把logit的变化和优势联系起来，导致缩放项消失了。
  • 不管动作初始概率是多少，更公平地对待所有动作的优势。

$${\theta }_{k+1}={\theta }_k+\eta F^{-1}{\mathrm{\nabla }}_{\theta }J({\theta }_k)$$$$z_{s,a}^{k+1}-z_{s,a}^k=\eta \cdot A(s,a)$$$$H({\pi }_{\theta }^{k+1})-H({\pi }_{\theta }^k)\approx -\eta \cdot {\text{Cov}}_{a\sim {\pi }_{\theta }^k(\cdot \mid s)}(\log {\pi }_{\theta }^k(a\mid s),A(s,a))$$

普通策略梯度vs自然策略梯度

特征	普通策略梯度 (VPG)	自然策略梯度 (NPG)
优化空间	参数空间 ($\theta$)	策略空间 (动作的概率分布)
步长含义	在参数最陡峭的方向上迈出固定的一步。	在最优方向上产生一个固定大小的策略变化（KL散度）。
Logit 变化	$\mathrm{\Delta }z\propto {\mathit{\pi }}_{\mathit{\theta }}\mathbf{(}\mathit{a}\mathbf{)}\mathit{s}\mathbf{)}\cdot A(s,a)$	$\mathrm{\Delta }z\propto A(s,a)$
熵变化项	$\text{Cov}(\log \pi ,\mathit{\pi }\cdot A)$	$\text{Cov}(\log \pi ,A)$
优点	实现简单。	更稳定，对参数化不敏感，能避免策略过早崩溃。
缺点	对参数化敏感，可能迈出毁灭性的大步。	计算昂贵（需要计算并求逆费雪矩阵）。

核心方法：打破性能瓶颈

背景

问题

• 熵坍塌，熵和协方差相关，熵正则无效。
• 仅少量token 协方差特别大，导致熵崩溃。
  • 仅0.02%的高协方差tokens的平均协方差值是整体平均值的1800倍以上

核心思想

• 精准打击协方差特别大的token即可。

协方差计算公式

• token-level 协方差，输出token $y_i$的协方差
• 注意协方差2个变量是：$y_i$的对数概率/初始信念和logit变化/动作优势/信念变化。
  • 下图公式logit变化是以自然策略梯度为计算的。

$$\text{Cov}(y_i)=(\log {\pi }_{\theta }(y_i)-\underset{\mathrm{对}\mathrm{数}\mathrm{概}\mathrm{率}\mathrm{均}\mathrm{值}}{\underbrace{\frac{1}{N}\sum _{j=1}^N\log {\pi }_{\theta }(y_j)}})\cdot (A(y_i)-\underset{logit\mathrm{变}\mathrm{化}\mathrm{均}\mathrm{值}}{\underbrace{\frac{1}{N}\sum _{j=1}^{N}A(y_j)}})$$

Clip-Cov/高协方差裁剪

Clip-Cov

背景

• 忽略限制高协方差token。

核心思想

• 随机选择一小部分高协方差token，在梯度更新中，分离并忽略掉他们的梯度 detach()
• 冷却机制，忽略掉最强正反馈信号token，防止他们完全主导学习过程，保留其他可能性。

筛选过程

• 计算每个token的协方差

• 设置协方差筛选范围上下限 $[{\mathcal{w}}_{\text{low}},{\mathcal{w}}_{\text{high}}]$，一般可设为平均协方差的500倍。

• 筛选高协方差token：设置筛选比例$r=0.02$，从中筛选$r\ast N$个token，记录index，用于clip掉。

  $$I_{\text{clip}}=I\sim \text{Uniform}(\{i\mid \text{Cov}(y_i)\in [{\mathcal{w}}_{\text{low}},{\mathcal{w}}_{\text{high}}]\},\lfloor r\ast N\rfloor )$$

• 对高协方差token：一律detach 梯度，不做更新

  $$L_{\text{Clip-Cov}}(\theta )=\{\begin{array}{ll}{E}_t[\frac{{\pi }_{\theta }(y_t\mid y_{<t})}{{\pi }_{{\theta }_{old}}(y_t\mid y_{<t})}\cdot A_t]& t\notin I_{\text{clip}}\\ 0& t\in I_{\text{clip}}\end{array}$$

KL-Cov/高协方差限制

KL-Cov

背景

• 限制高协方差token的更新幅度。

核心思想

• 不完全忽略高协方差token，对高协方差token施加KL惩罚，限制更新幅度不能太大。

具体方法

• 计算所有token的协方差。
• 筛选高协方差token：所有token按协方差从高到低排序，选择top-k比例的token

$$I_{\text{KL}}=\{i\mid \text{Rank}\text{Cov}(y_i)\le k\ast N\}$$

• 对高协方差token：增加KL惩罚，限制更新幅度$$L_{\text{KL-Cov}}(\theta )=\{\begin{array}{ll}{E}_t[\frac{{\pi }_{\theta }(y_t\mid y_{<t})}{{\pi }_{{\theta }_{old}}(y_t\mid y_{<t})}\cdot A_t]& t\notin I_{\text{KL}}\\ E_t[\frac{{\pi }_{\theta }(y_t\mid y_{<t})}{{\pi }_{{\theta }_{old}}(y_t\mid y_{<t})}\cdot A_t-\beta \cdot D_{\text{KL}}({\pi }_{{\theta }_{old}}(y_t|y_{<t}),{\pi }_{\theta }(y_t|y_{<t}))]& t\in I_{\text{clip}}\end{array}$$

Clip-Cov+KL-Cov vs Clip-Higher

和Clip-Higher 对比

Clip-Higher

• 放宽限制，允许更多低概率且高优势的token参与梯度计算，这些token恰好是负协方差的、增加熵。
• 间接、无意中，做了正确的事情。

Clip-Cov, KL-Cov

• 不通过概率筛选，直接使用协方差这个根本指标作为阈值。
• 对熵的控制更精准、直接。

算法实验

实验设置

Clip-Cov & KL-Cov 实验配置

模型

• Qwen2.5-7B, Qwen2.5-32B

Baseline

• GRPO, GRPO+Clip-Higher(0.28)

任务

• 训练数据：DAPO-MATH-17K

• 评测数据：MATH500, AIME24, AIME25, AMC, Omini-Math, Olympiad-Bench, Minierva

超参

• 训练Rollout

  • bs=256, rollout.n=8, temperature=1

• 评估

  • AIME+AMC：temperature=0.6
  • 其他测试集：贪婪解码

• Clip-Cov

  • 比例r：$r=2\cdot {10}^{-4}$, CLIP上下限 $[{\mathcal{w}}_{\text{low}}=1,{\mathcal{w}}_{\text{high}}=5]$

• KL-Cov

  • top-k比例

    $$k=\{\begin{array}{ll}2\cdot {10}^{-3}& \text{Qwen2.5-7B}\\ 2\cdot {10}^{-4}& \text{Qwen2.5-32B}\end{array}$$

  • $\beta =1$

• max_generation_length = 8192

关键结果

关键结果

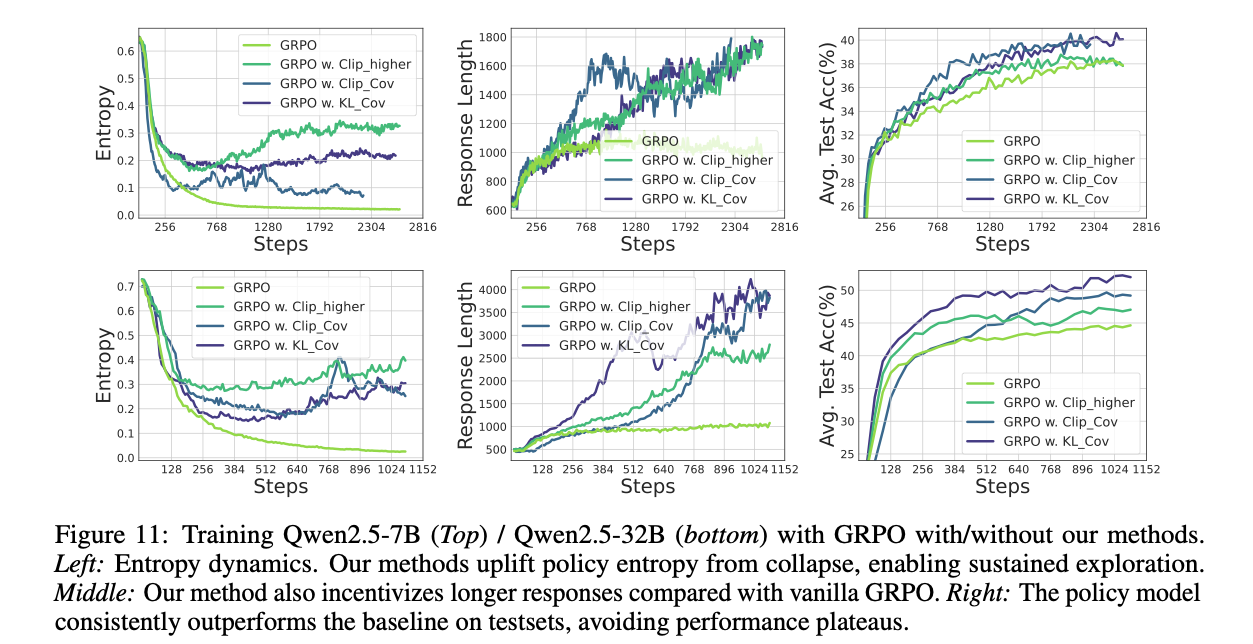
• Clip-Cov和KL-Cov 效果好。7B平均提升2.0pt，32B提升6.4pt。
• 新方法维持了高策略熵，实现了持续探索和学习。
  • 基线方法熵耗尽时，KL-Cov仍能把熵维持在10倍以上水平。
  • 激励更长回答。
  • 避免性能饱和，持续稳定提升。
• Cov方法在大模型上效果更好，展现出良好的Scaling。
  • 解除了探索限制，能更好释放大模型潜能。
• 干预可控且高效。
  • 可干预：Clip-Cov 裁剪比例、上下限；KL-Cov top-k比例、系数等。
  • 干预高效：干预少量token即可改变训练过程的熵动态
• 熵控制的哲学
  • 熵崩溃是由少部分高优势高概率token引起的，是由少数点坍塌引发的连锁反应。
    • 精准扶住关键点，就能稳住整个系统。
  • 熵和性能并非直接关系。
    • 并非 维持的熵越高、性能就越好。不同的熵水平，可能达到相似性能。
    • 什么样的熵才是最优的呢？

性能好

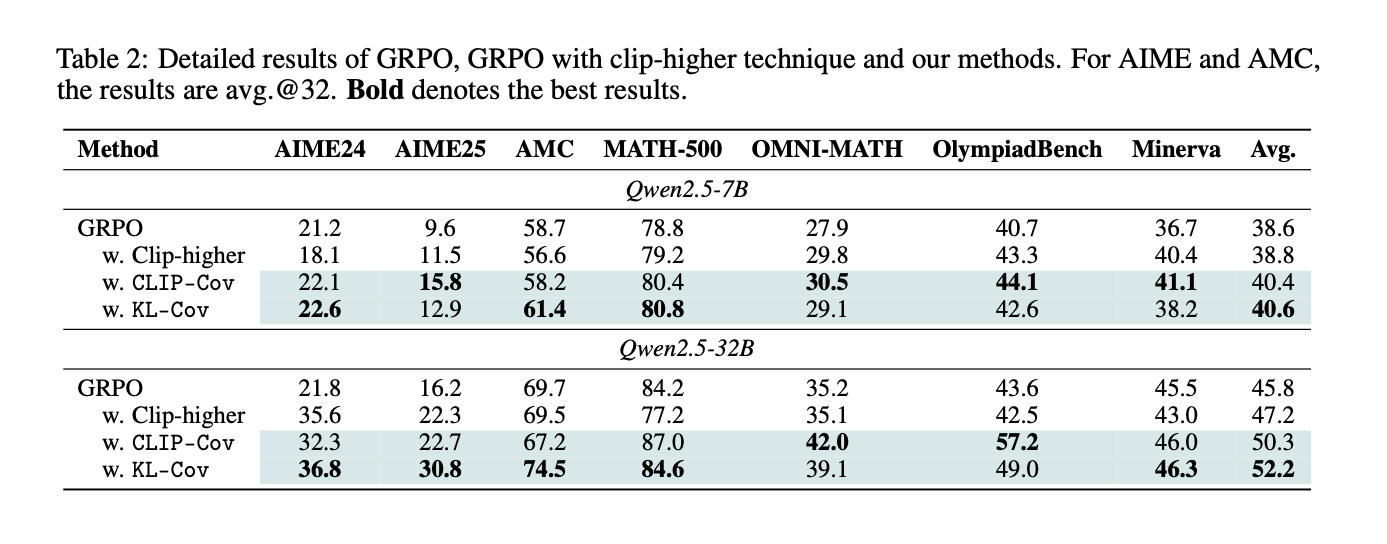
维持了高策略的熵，实现持续探索和学习。

未来方向

⛳未来方向

未来方向

• 寻找最优熵值
  • 是否存在？动态控制熵策略，前期探索，后期收敛。需要根据任务难度自动调整参数。
• 深入分析关键token
  • 有什么特征？
• 泛化到其他领域和算法
• 利用可预测性提升RL效率

相关文章

小心

• 【chapter5】从熵理解：强化学习中如何鼓励探索
• RL中的熵机制：策略熵坍缩分析与协方差正则化方法