免模型
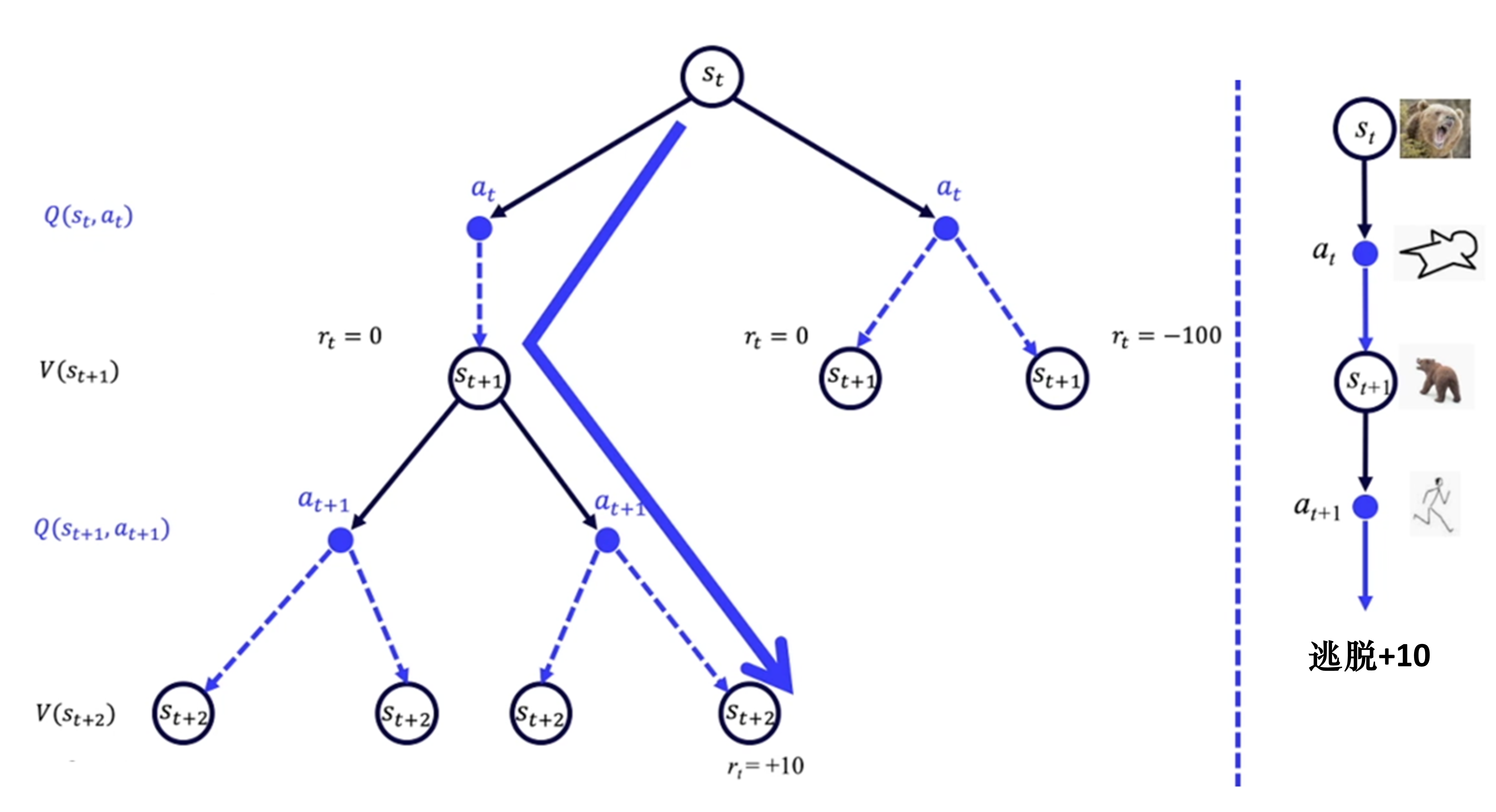
免模型试错探索,环境信息未知,没有概率可言,熊何时出现做什么,一切都未知。
RL可以应用在完全未知随机的环境,像人类一样,通过尝试不同的路来学习,慢慢了解哪个状态动作会更好。
免模型预测
蒙特卡洛方法
思想
核心思想
特点
- 不依赖:
模型(状态转移/奖励函数);不依赖:动态规划自举方法 - 基础MC是on-policy的,可通过 重要性采样 变成off-policy。
缺点
- 只适用于有终止状态的马尔可夫决策过程 (MC方法通用问题)
- 依赖每个轨迹的真实回报
具体做法
- 给定策略
,从状态s开始, 智能体和环境交互,采样多条轨迹 - 计算每条轨迹的真实回报
,用 所有轨迹的平均回报来估计价值函数
- 如果估计Q函数,从状态s开始,强制执行动作a,再进行采样即可。
- 有了Q,做贪婪策略,就能做策略改进了。
价值函数估计(经验均值)
- 每回合,若在时间t状态s被访问,则更新总访问数和总回报
- 总访问数:
- 总回报:
- 总访问数:
- 通过
回报平均,来估计状态s的价值: - 缺点:需拿到所有的轨迹的回报后,才能求平均、更新价值函数
增量更新
核心思想
- 做增量计算:
新估计值=旧估计值+ 学习率 *(目标值 - 旧估计值),
- 蒙特卡洛误差
- 误差项=
轨迹真实回报-期望回报,希望估计回报逼近真实回报 - 如果
,说明估计值偏低;如果 ,说明估计值偏高,需要调整。
- 误差项=
学习率
如果较大(接近1),更新比较激进,大幅朝着新回报值
靠拢 如果较小,更新会比较保守。
优点
- 不用保存所有样本数据,每采样一个新轨迹,就可以更新价值函数,做到
回合级更新 - 只更新轨迹上的所有状态,和轨迹无关的不用更新
- 节省资源
缺点
- 需等一个完整回合结束后,才能算出每个状态的真实收益,利用收益去更新价值函数。
- 不适用于持续性任务、步骤很长的回合制任务。
对比动态规划自举更新
- 用
上一时刻的V来更新当前时刻的V(贝尔曼期望备份)
MC vs DP
环境模型
- DP:需已知环境模型(状态转移概率和奖励函数)
- MC:无需完整环境模型,只需通过
环境交互来收集经验即可
策略更新
更新方式
- DP:全局更新,需更新所有可能状态和动作。
- MC:局部更新,只更新轨迹上的状态。通过一个经验的回报,就能做更新。
计算量
- DP:计算量大。需计算所有可能的动作和状态,空间很大时,难以计算,非常慢。
- MC:计算量小,只需更新轨迹上的状态动作即可。
适用场景
- DP:状态空间小、模型已知
- MC:
状态空间大、模型未知
收敛性
- DP:保证收敛到最优解
- MC:可能需要更多迭代次数才能收敛,受到样本随机性影响。
动态规划需更新所有状态来求期望:
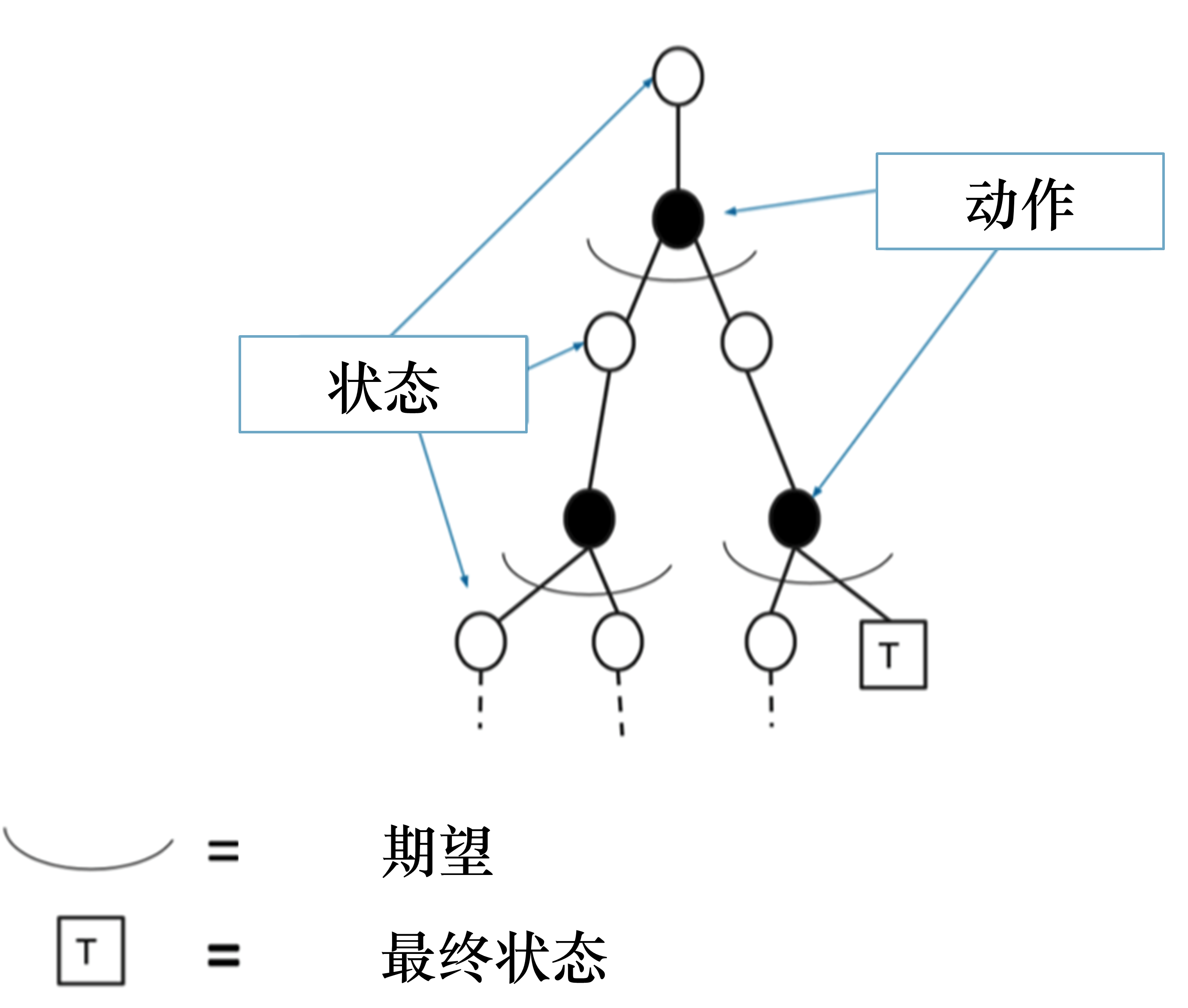
蒙特卡洛只更新轨迹线上的状态:
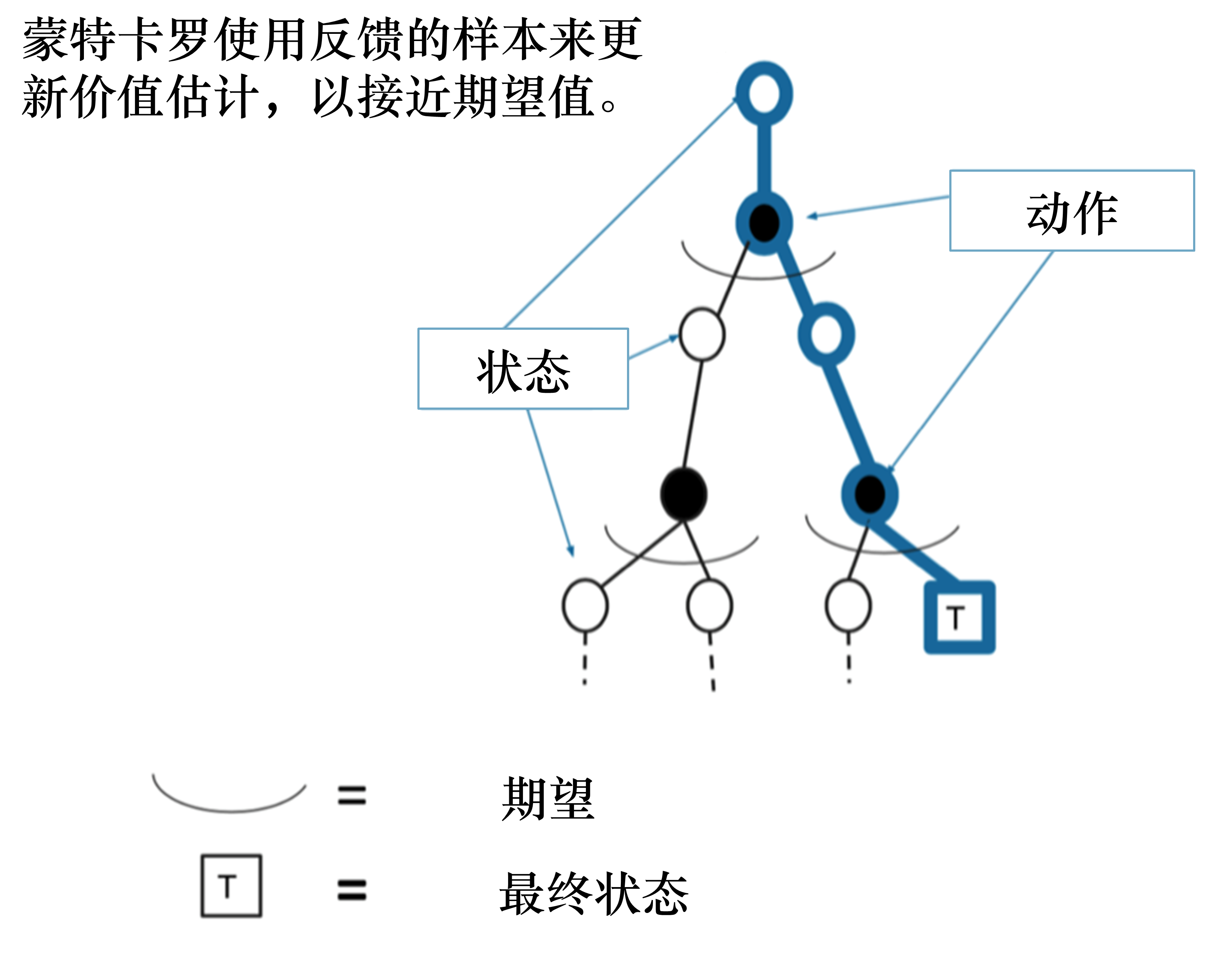
时序差分方法
一步时序差分
背景
- MC需采样
整个回合才能更新,TD只需采样1步就可以更新价值函数。 - 单步采样
- 可以快速适应环境变化。
- 但只考虑一步的未来,导致自举方法是一种
有偏估计。
核心思想
使用
MC采样+DP自举估计轨迹回报。- 用V函数的自举估计值来代替MC中的真实轨迹回报
- 用V函数的自举估计值来代替MC中的真实轨迹回报
无需等待轨迹结束,在每一步都可更新价值函数
一步时序差分TD(0)
- 采样1步
,自举估计出轨迹回报作为 目标值,来更新价值函数- 自举:用1个估计值,来更新另1个估计值
- 类比 增量MC
TD目标和TDError
TD目标 (采样1步+自举估计回报)
- 采样1步:走1步后得到的实际奖励
- 自举估计:用上一轮的
来估计当前轮的 - 用之前的估计来估计
- 用之前的估计来估计
TD error
实际走一步看到的回报和 先前对当前状态的预测的 差距。:说明实际情况比预想的要好。 - 学习
来逼近 时序差分目标/真实回报 :平衡短期奖励和长期奖励,通常在0.95-0.99之间。
- 类比MC Error
TD&MC 方差和偏差
TD (近视眼/有偏估计)
- 自举1步,只能看到下1步。可能
不准确(偏差大),但比较稳定(方差小)。 - 用下一步状态估计值
来更新当前状态估计值 ,TD目标本身就是不准确的,这就导致了 偏差 - 但TD只依赖下一个状态,每次更新变动比较小,因此
方差小
MC (远视眼/无偏估计)
- 完全采样,看到整个回合。所以
比较准确(偏差小),但经常出现波动(方差大)。 - MC用实际真实回报,所以是
无偏的; - 但需等待整个回合结束,回报是多个随机事件叠加结果,因此
MC更新目标波动大,即方差比较大。
TDError 优势偏差方差问题
0. 优势函数公式
1. TD Error 有偏估计 问题分析
- 如果
是无偏的,能准确估计出状态价值 - 那么TD Error
也是无偏的,能准确估计出优势。
- 那么TD Error
- 但没有如果,现实
往往很难估计出状态价值 发生偏差时, 无论采样多少次,都无法估算真正的优势函数- TDError 一定是有偏的,从而引发
系统性偏差。
2. TD Error 高偏差 解决办法
价值函数估计不准, 就少信赖它。- 采样多步回报,
多信赖依靠采样实际奖励。
3. n步TD 高方差 问题分析
- 由于随机策略及环境转移等内容,所以
是 随机变量。 n步采样、相比之前单步采样,方差更大。
4. n步 TD 高方差 解决方法
TD(λ) / λ-return算法
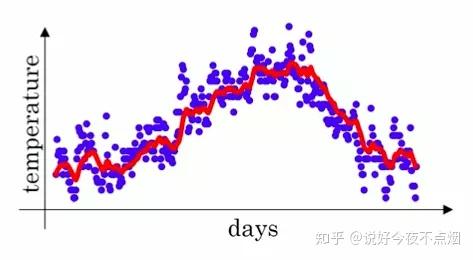
指数移动加权平均
:到第t天的平均值, :第t天的温度值, 是 衰减系数
- 指数加权平均:作为原数据的估计值,可以抚平短期波动,起到
平滑作用 - 离当前越近,
权值越大;离当前越远,权值越小(指数递减),也有一定权值
红色的数据比蓝色的原数据更加平滑,少了很多噪音,并且刻画了原数据的趋势。
在梯度下降法中的应用
- 纵轴方向,平均过程中正负摆动相互抵消,平均值接近于零,摆动变小,学习放慢。
- 横轴方向,因为所有的微分都指向横轴方向,因此平均值仍然较大,向最小值运动更快了。
- 在抵达最小值的路上减少了摆动,加快了训练速度。

n步回报
背景
- 1步TD:高偏差、低方差。MC:低偏差、高方差。
- 在
单步采样和MC 回合采样之间,做折中。
核心思想
往前采样n步,再更新,不局限于1步,也不必等到回合结束👍。- 比如往前走2步,得到2步的回报,再使用自举来更新价值。
- 考虑时刻
的回报。
时序差分目标
:时刻 到时刻 的n步回报。 :在时刻 的价值估计。
- 增量式参数更新
n的选择
- 如果固定n
- n较小,学习
速度快,但可能不准确,但方差小 - n较大,学习
速度慢,但可能更准确,但方差大
- n较小,学习
- 不同的任务可能需要不同的n值
- 有些状态需要长远回报,有些状态需要较短回报
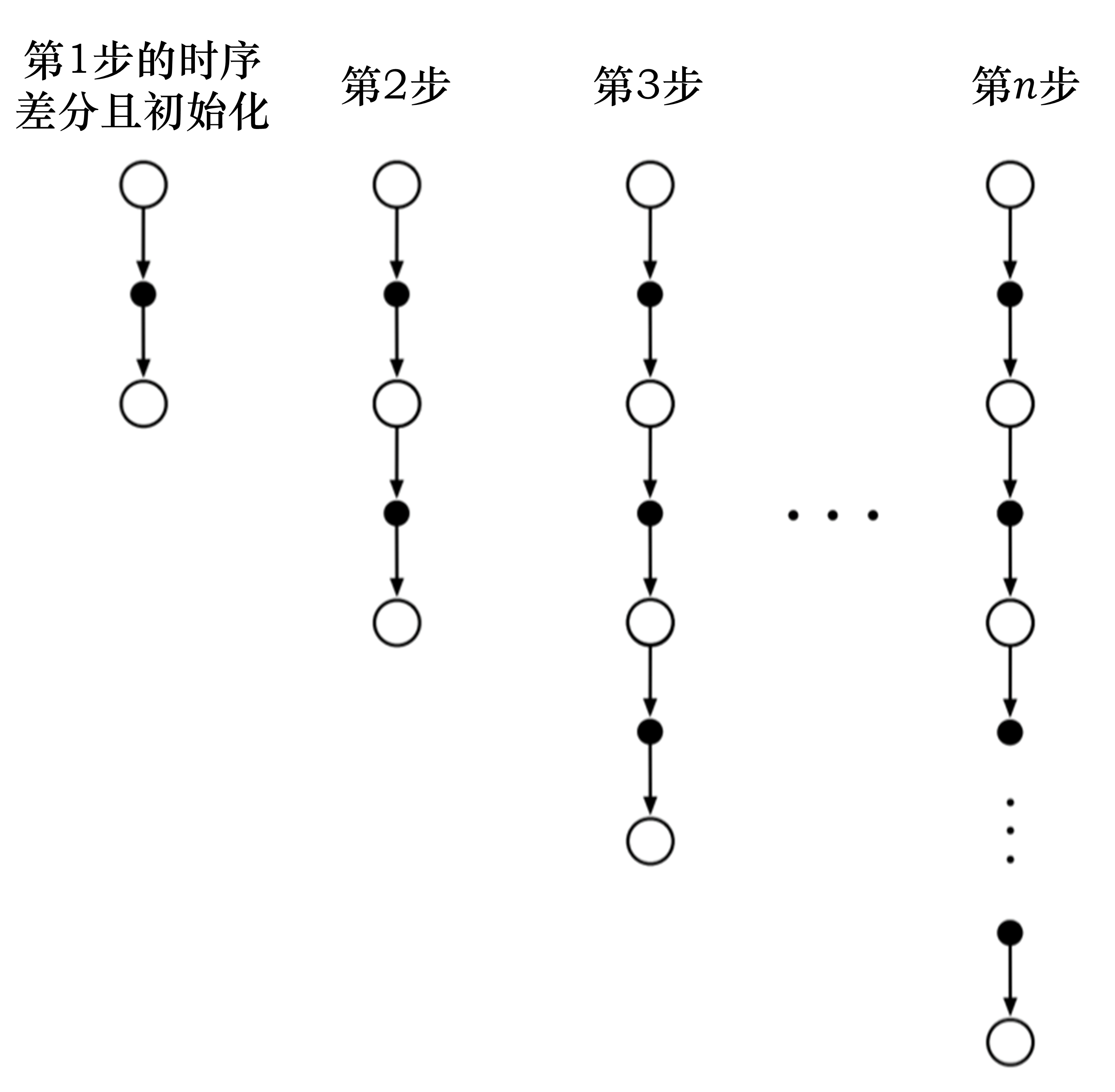
λ 回报
问题背景
- TD 高偏差、低方差;MC 高方差、低偏差。
- n步回报,n难以确定;若固定n,所有状态都使用相同步长的回报,不够灵活。
λ回报公式
λ回报- 对多个n步回报估计,做
λ权重加权平均,权重衰减,平衡方差和偏差 - 共有多个n步估计量,步数从1到
- 对多个n步回报估计,做
定义
- 推导过程 (分离终止项推导见下文)
推导结果
参数更新
权重
:估计量 的加权/衰减权重 - n越大,
衰减越高
- n越大,
为何需要乘以
需要保证加权权重为1
仅看权重,
权重为等比数列- 等比数列求和公式:
,首项为 、比为 。
- 等比数列求和公式:
权重求和:。 时, - 如果不乘
:权重和为 - 如果乘以
,权重和为1
统一理解
统称为 权重、归一化权重,权重和为1。对所有n步回报加权平均。
背景
无限求和公式 不适用于有限回合。
回合
在时间T结束, 时间T以后不再有状态、没有回报。当
,即 时, 回合已经结束,无法通过无限公式计算- 因为无法获取
, , 无法计算 - 但后面的所有即时奖励回报都为0。
- 因为无法获取
意味着,
时, 就等同于完整的MC回报
分离终止项
- 作用:把无限求和公式分成2部分
第1部分:从
开始时间t到回合结束时间T之间的所有n步回报第2部分:
超出结束时间 后的 n步回报平均值,详见下文公式推导过程:推导出来后面的权重 :推导出来后面的回报求和内容
推导过程
- 推导过程
- 推导结果
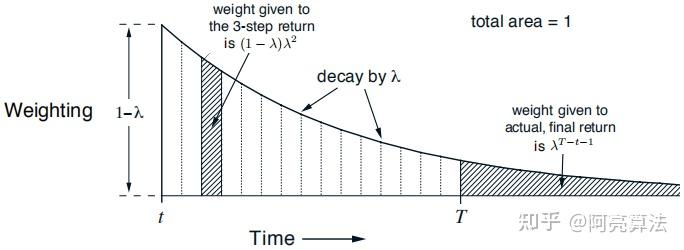
TD(λ) 、TD(0)和TD(1)
TD(λ)
λ 越小:趋近于单步TD,偏差越大,方差越小λ 越大:趋近于MC,偏差越小,方差越大
TD(0)
,完全衰减,退化为 单步TD回报。
TD(1)
,完全不衰减, 退化为 完整MC回报会导致无穷级数发散,不能直接通过 去乘积计算 - 需用分离终止项公式
TD(λ) 价值函数更新
直接使用λ回报替换TD目标来更新Q函数 (表格法)
函数参数法
- 用神经网络来近似价值函数,权重为
:价值函数对权重 的梯度。
资格迹
背景
- 在实际运算中,
回报需存储所有历史信息。工程复杂、内存消耗高、不适合在线学习决策等。 - 引入
资格迹(Eligibility Traces),高效计算λ回报的一种技巧。
资格迹
- 资格迹作用
- 记录了过去回合中,哪些状态被访问过,以及对学习结果影响程度。
- λ回报的复杂计算 变成 更简单、增量式的更新方式,避免大量重复计算
表示t时刻的资格迹,一个加权的价值函数梯度和。 是 折扣因子,控制 资格迹的衰减速度。
- 当状态被访问时,资格迹会增加。早期访问过的状态,资格迹按
衰减。
使用资格迹
- 按照如下公式更新价值函数。只需计算
TD误差和资格迹,无需计算复杂的回报。
- Sara(λ)
- Q-Learning(λ)

MC vs TD vs n步TD vs TD(λ)
核心公式对比
MC 采样
V函数 更新
MC Error
单步TD
V函数 更新
TD Error
n步 TD
定义
V函数 更新
TD Error
TD(λ)
定义
V函数 更新
TD Error
概念对比
时序差分
- 可以在线学习,每走一步就能更新;在知道结果之前就能学习,更快速灵活
- 可以从不完整序列学习,可以在连续环境下进行学习
- 利用了马尔科夫性质
- 更新时使用了自举(更新时使用了估计),一部分采样,一部分自举。
- 以采样方式得到不完整序列,估计某状态后可能的奖励,不断采样持续更新价值
- TD方法在每个时刻都可以更新价值函数,是一种
高偏差、低方差的方法 - TD
有偏估计,可能无法准确预测未来收益,在延迟激励情况下,需很长时间才能把奖励传播到之前的状态,存在信用分配问题。
蒙特卡洛
- 不能在线学习,必须游戏结束时才能更新
- 只能从完整序列进行学习,只能在有终止的情况下进行学习
- 没有假设环境具有马尔科夫性质
- 没有使用自举
- 高方差 (预测值的变化范围、离散程度)
- MC方法需要用整个episode的经验去估计价值函数,是一种
低偏差、高方差的方法。
动态规划
- 有模型预测方法
- 使用了自举
自举采样对比
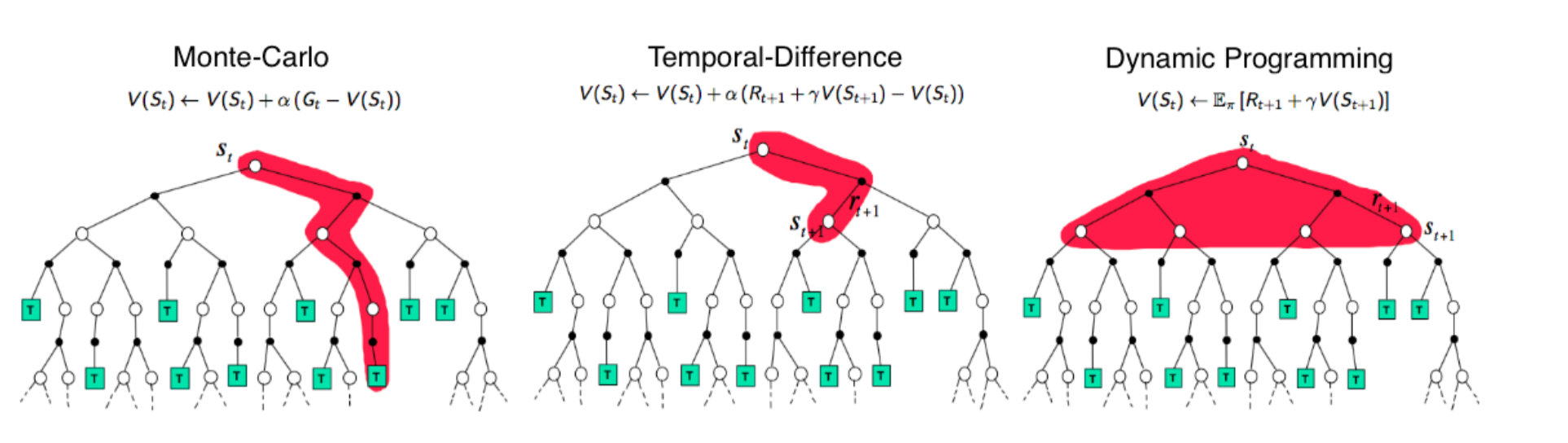
时序差分对比蒙特卡罗
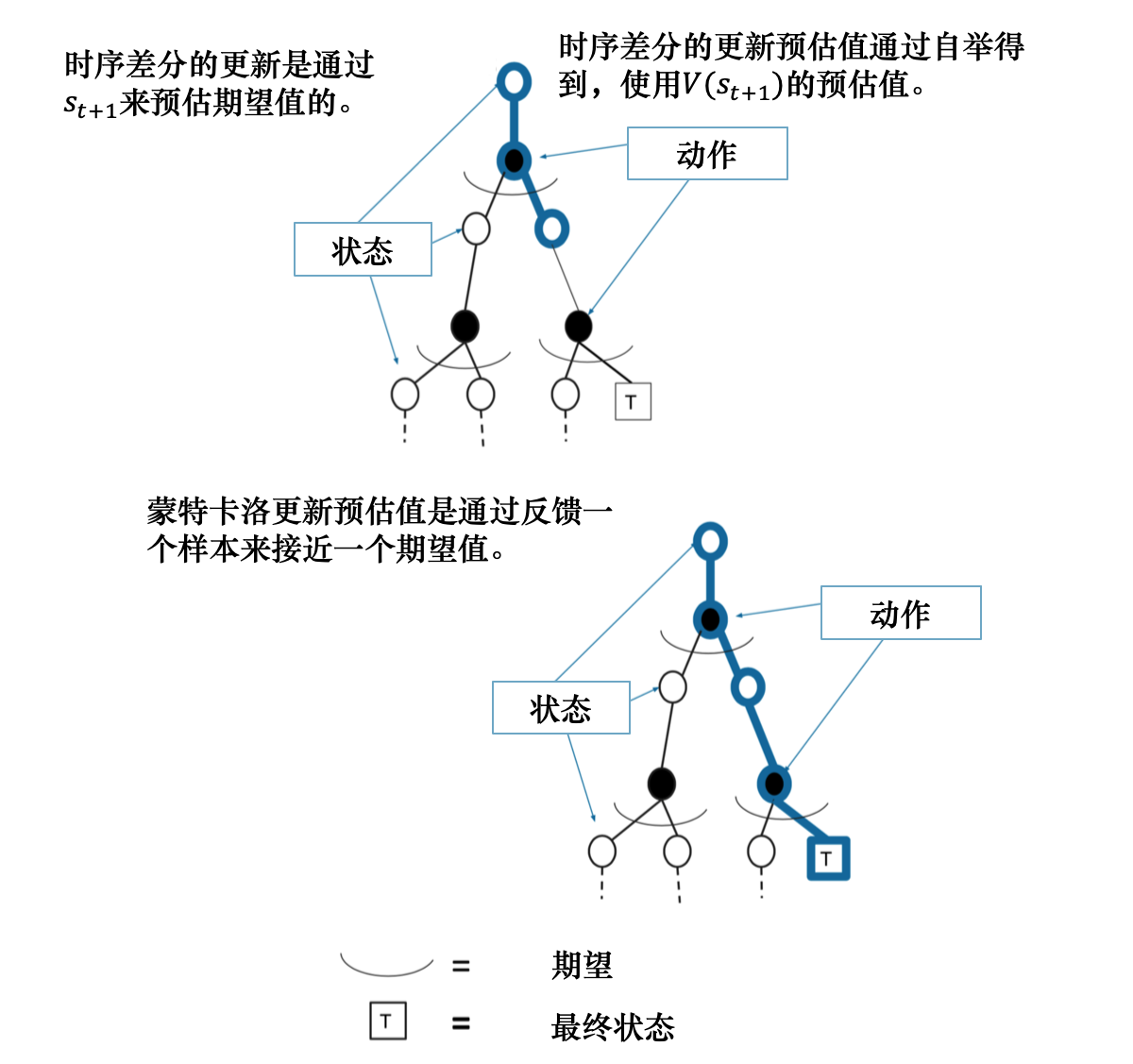
动态规划备份:直接计算期望
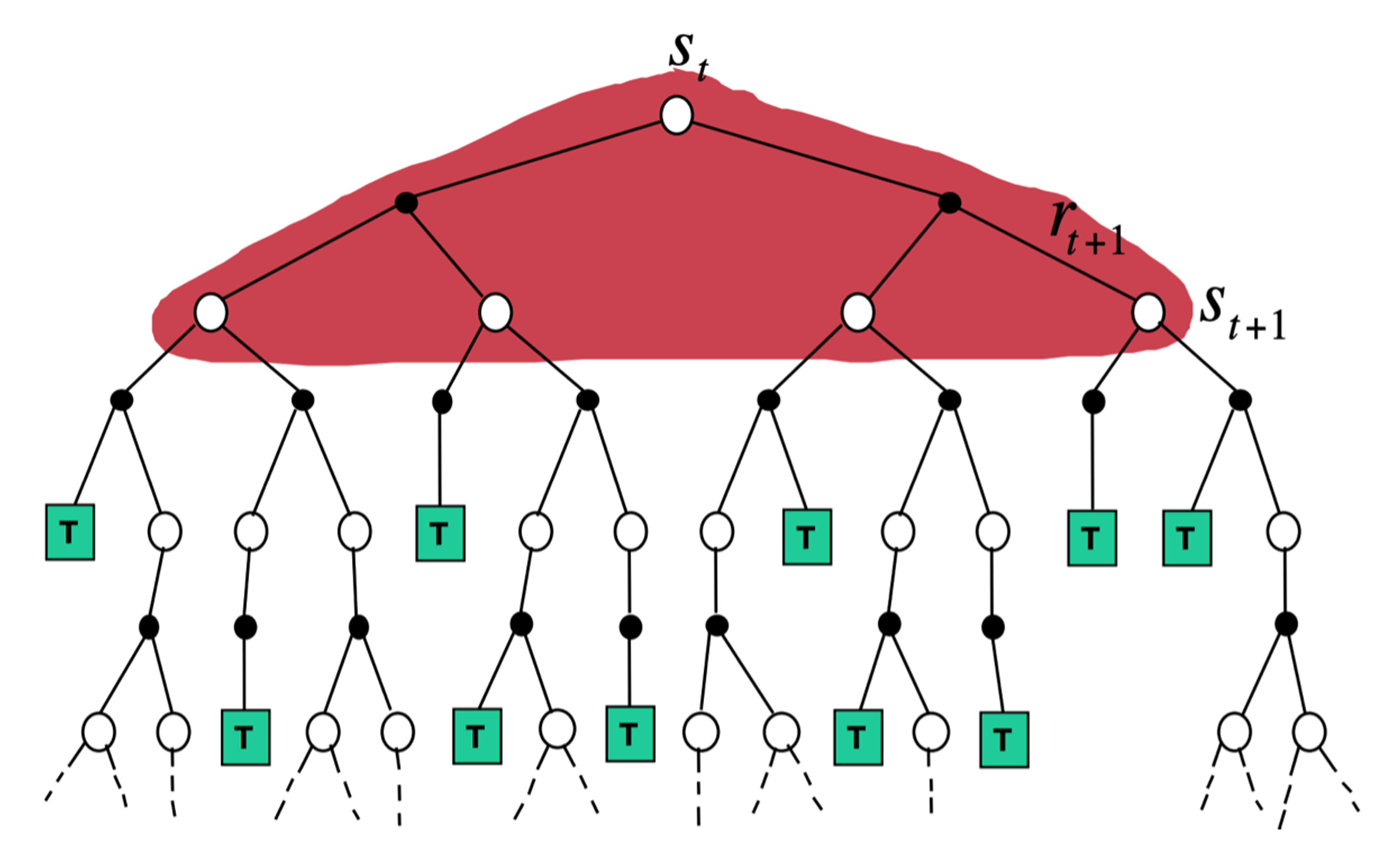
蒙特卡洛备份:采样一条支路计算,更新这条路径上的所有状态
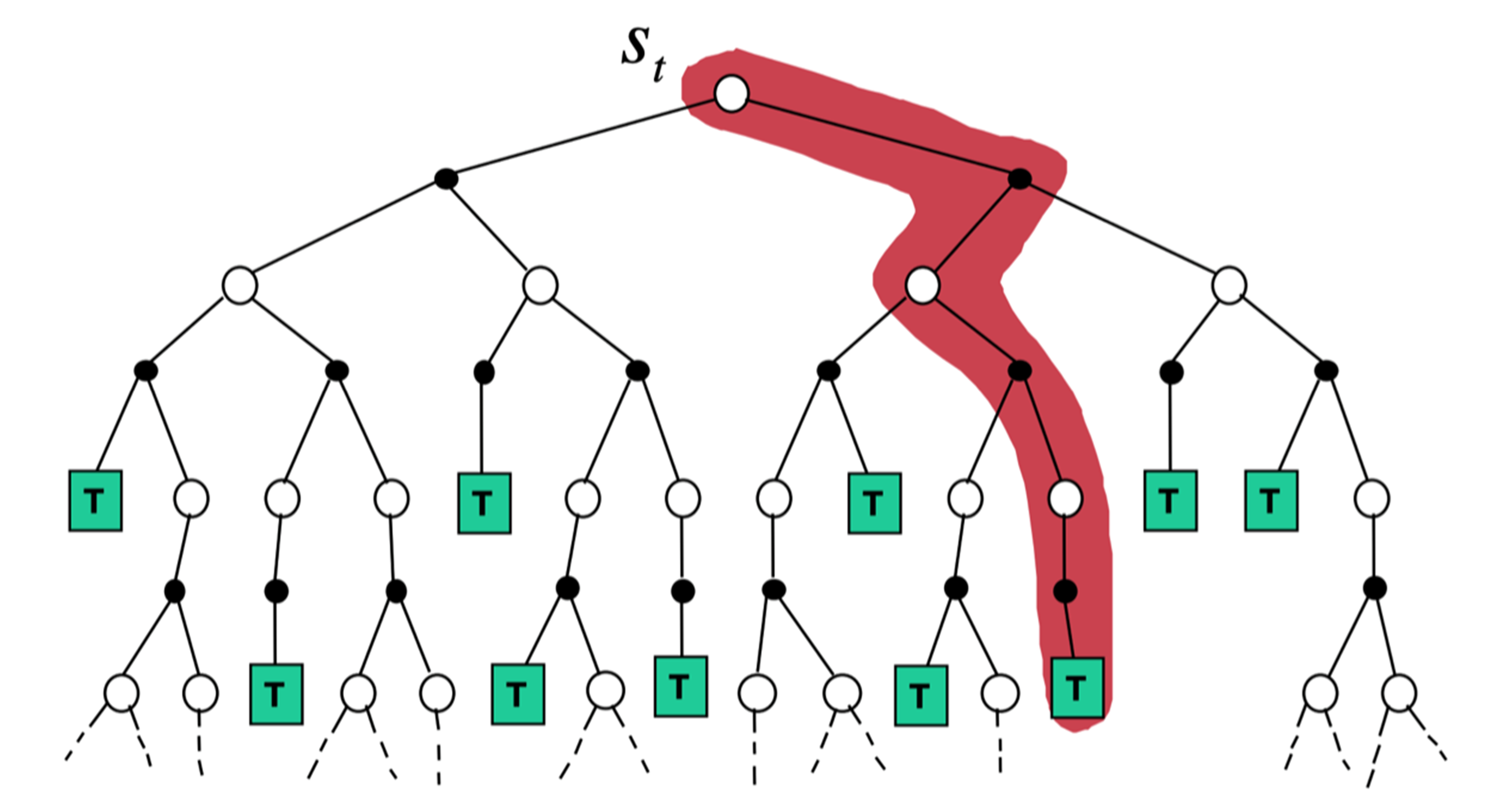
时序差分备份:采样+自举,从当前状态开始走几步,关注局部步骤
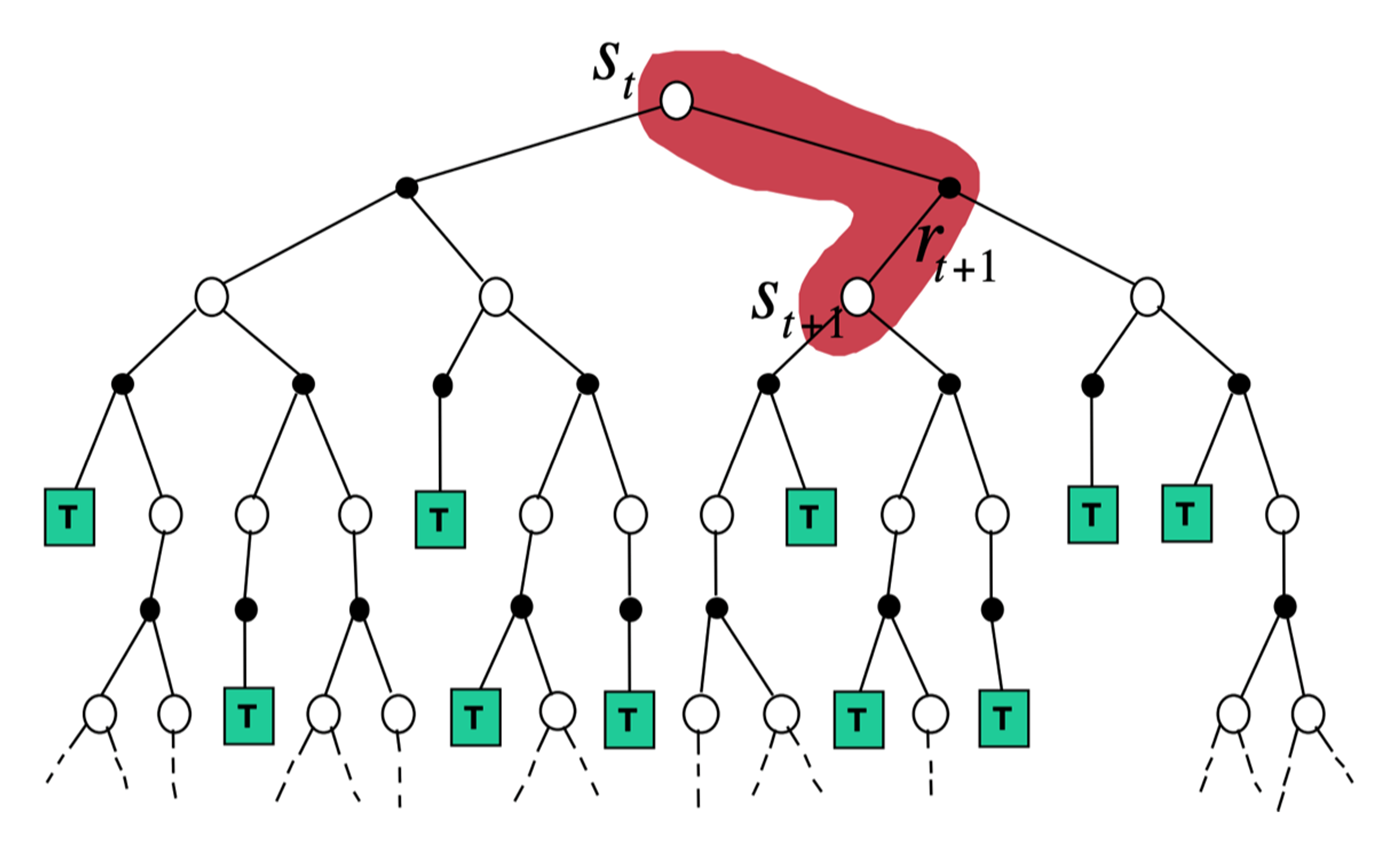
时序差分:需要广度,就变成动态规划;需要深度,就变成蒙特卡洛。
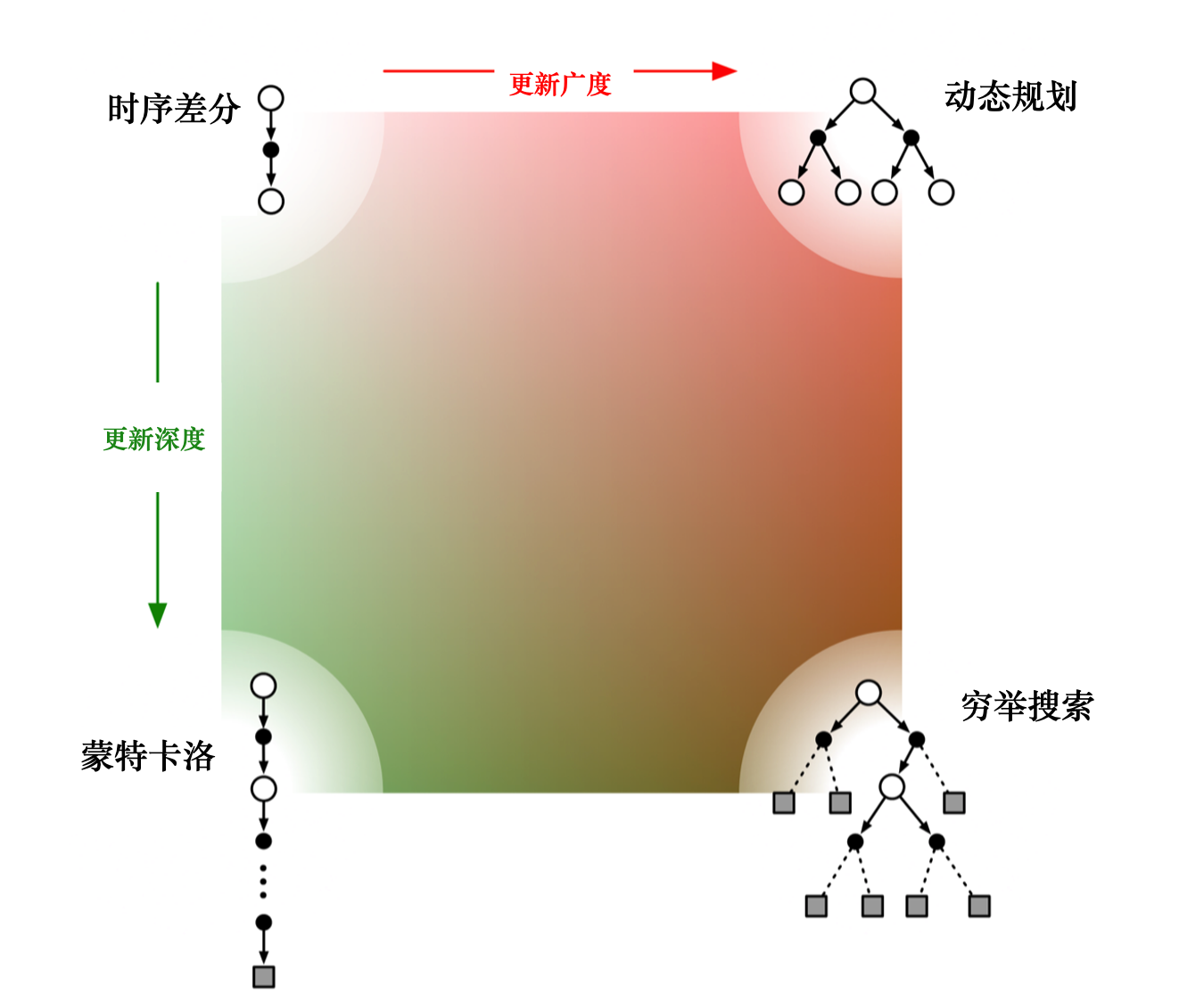
免模型控制
免模型控制是指不需要知道环境模型,进行寻找最优策略输出最有价值。Q-Learning和SARSA都是基于时序差分的算法。
广义策略迭代
狭义策略迭代
定义
有模型控制,通过
策略评估和策略改进,不断迭代直到值函数收敛。通过环境信息(
奖励函数、状态转移概率),来计算价值函数
缺点
- 依赖奖励函数和状态转移概率;免模型时,无法估计
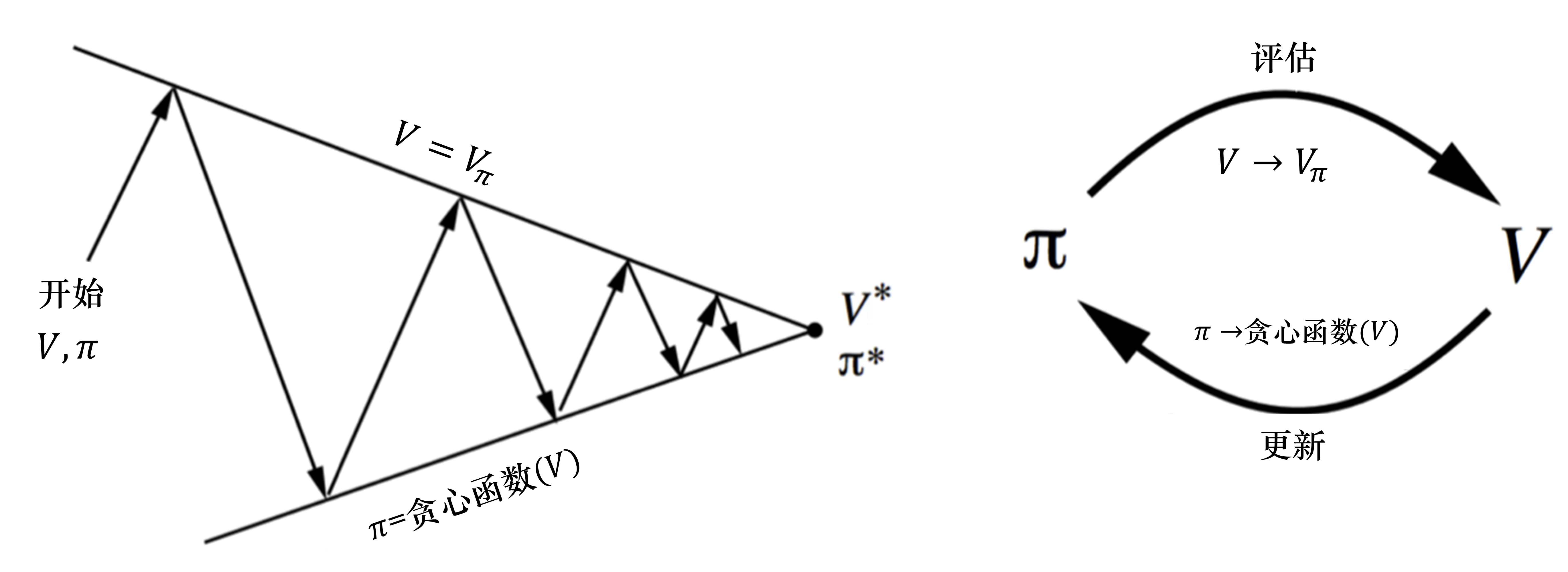
广义策略迭代
定义
- 免模型控制,引入
蒙特卡洛和时序差分,进行策略迭代 策略评估:用蒙特卡洛探索采样多个轨迹,平均轨迹价值,来估计Q函数
策略改进:直接选择最大的Q函数
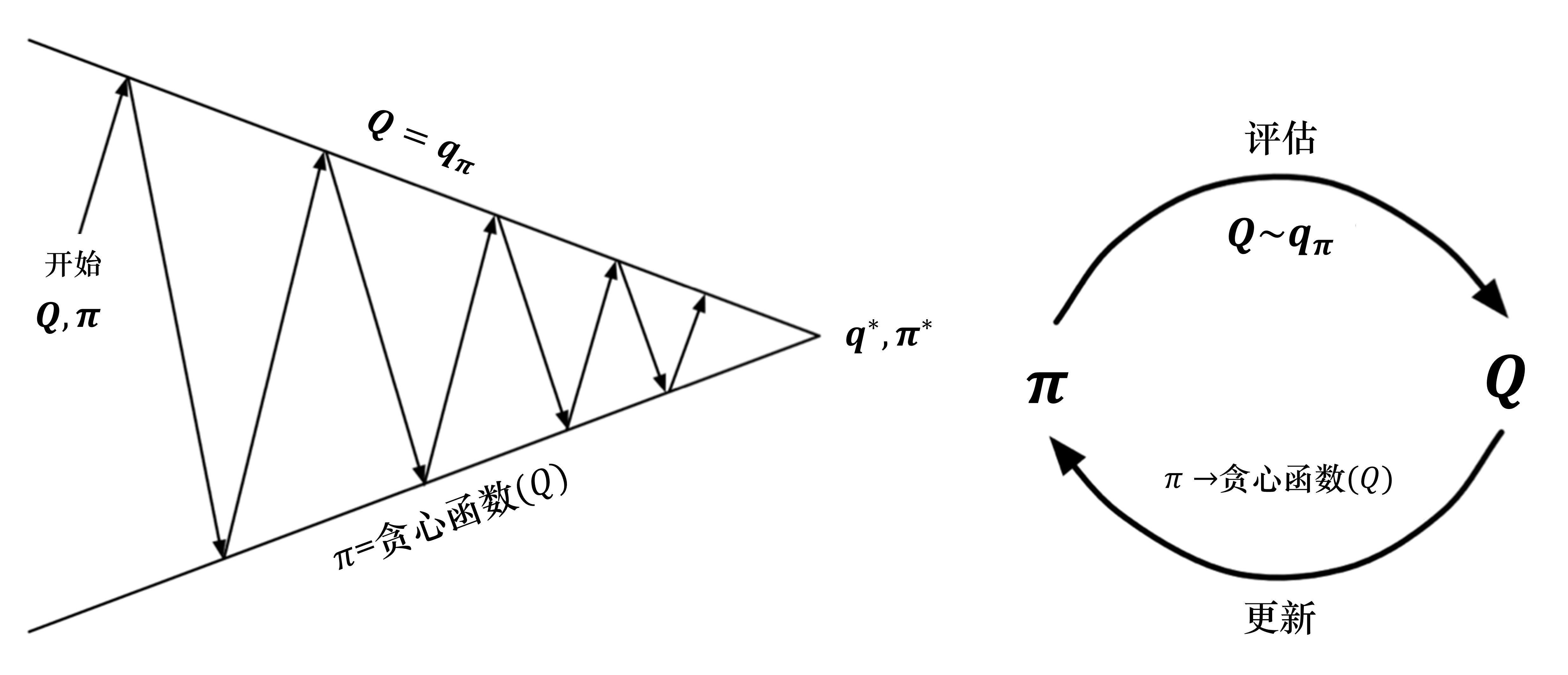
探索策略
- 一直基于某种思路工作,可能会比较好,
但也可能会走偏 换一种思路也许就会豁然开朗- 守旧不一定是坏事,
不能过度好奇心
- 为了保证足够的探索,以
概率随机选择一个动作 按时间步递减,如0.1 -> 0.01- 开始时不确定哪个动作较好,
花较多时间进行探索 - 后期逐渐稳定,
减少探索,降低
- 开始时不确定哪个动作较好,
定义
- 对
, 被选中的概率和 有关 - T为温度系数
- T很大,等概率选择;T很小,Q值更大的动作容易选中;T趋于0,只选择最优动作。
同策略异策略
行为策略 vs 目标策略
行为/探索/采样策略
探索环境的策略,采集很多轨迹经验,给行为策略进行学习- 像前线的战士,
希望充分探索环境,访问所有可能的状态和动作。 - 如:
策略评估,探索环境,采样估计Q函数
目标/学习/改进策略
通过经验稿子进行学习的策略,不用和环境进行交互- 像后方的军师,
尽可能利用已有的经验。 - 如:
策略改进,更新策略


同策略 vs 异策略
同策略/On-Policy
- 定义
- 行为/采样/
探索策略和 学习/改进/目标策略相同。 - 使用同一策略来搜集样本,通过样本学习并
更新原策略。
- 行为/采样/
- 优点
- 稳定,可以保证学习到的策略
收敛到最优策略 - 较好解决连续动作空间问题
- 稳定,可以保证学习到的策略
- 缺点
- 样本利用效率低
仅能用来更新当前策略,不能更新其他策略
- 样本利用效率低
异策略/Off-Policy
- 定义
- 行为/采样/
探索策略和 学习/改进/ 目标策略不同。 - 使用
行为策略探索到的经验轨迹,来优化目标策略。- 如从
经验回放或历史数据中学习。
- 如从
可是随机策略,但采取 贪心 使其不至于完全随机,是基于Q表格逐渐改进的。
- 行为/采样/
- 优点
- 学习效率高:旧策略的采样经验可
多次利用,节省资源 - 利用通过行为策略探索来学到最佳策略
行为策略可采用贪心算法,更加大胆,有可能探索到最佳策略 目标策略仍使用普通贪心算法,根据行为策略经验来采用最佳策略
- 可以学习其他智能体的动作
- 学习效率高:旧策略的采样经验可
- 缺点
- 需分布比较接近,避免偏差,避免训练不稳定
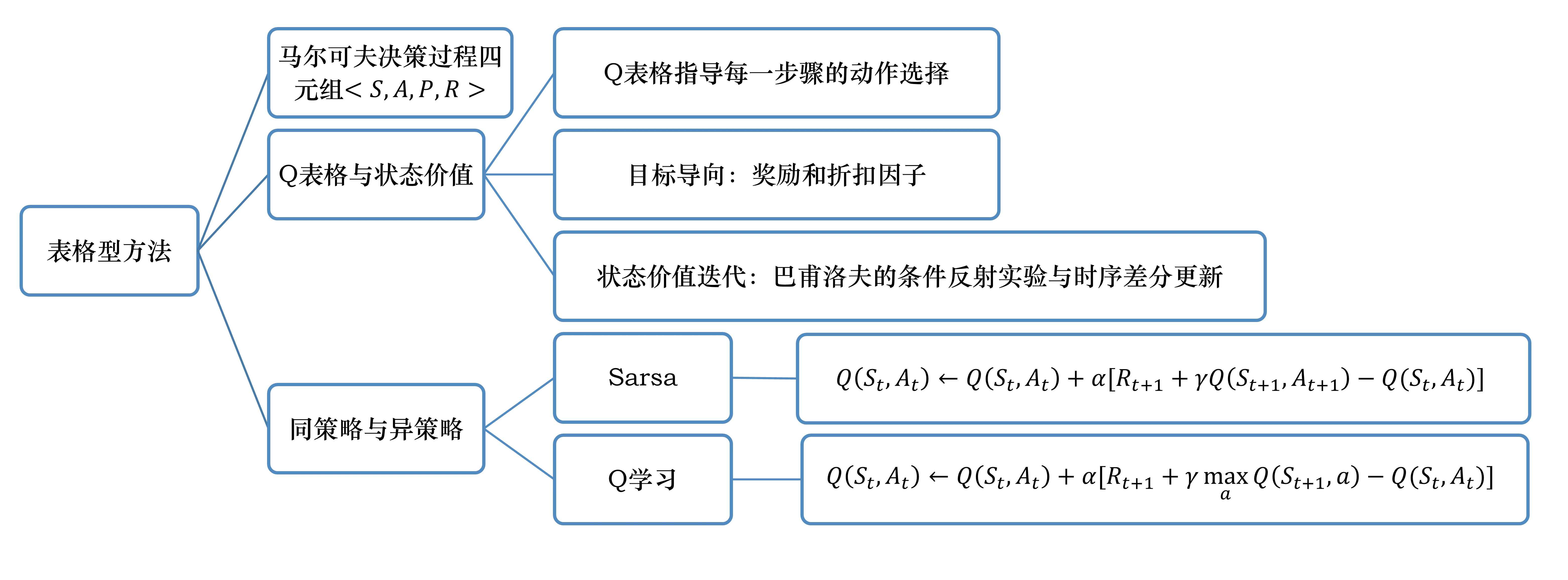
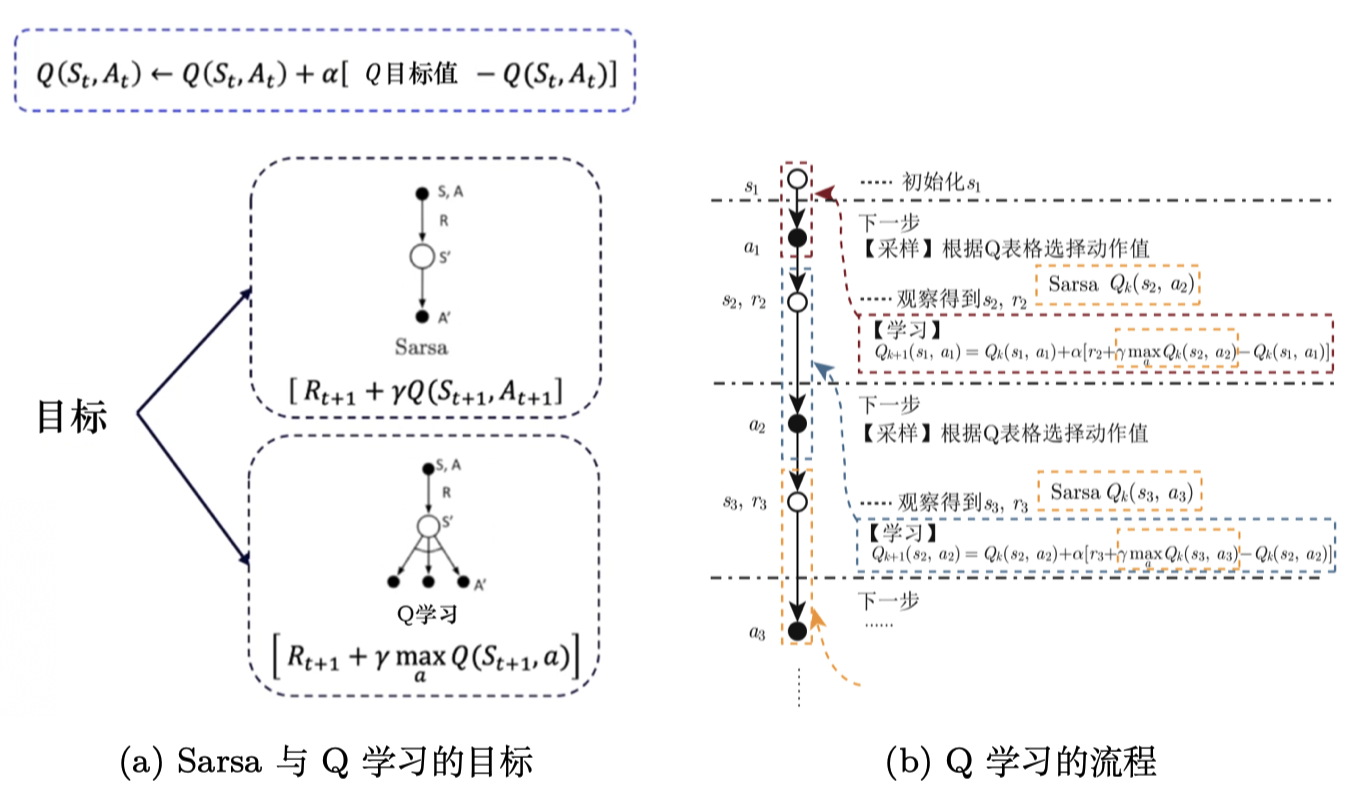
SARSA:同策略TD
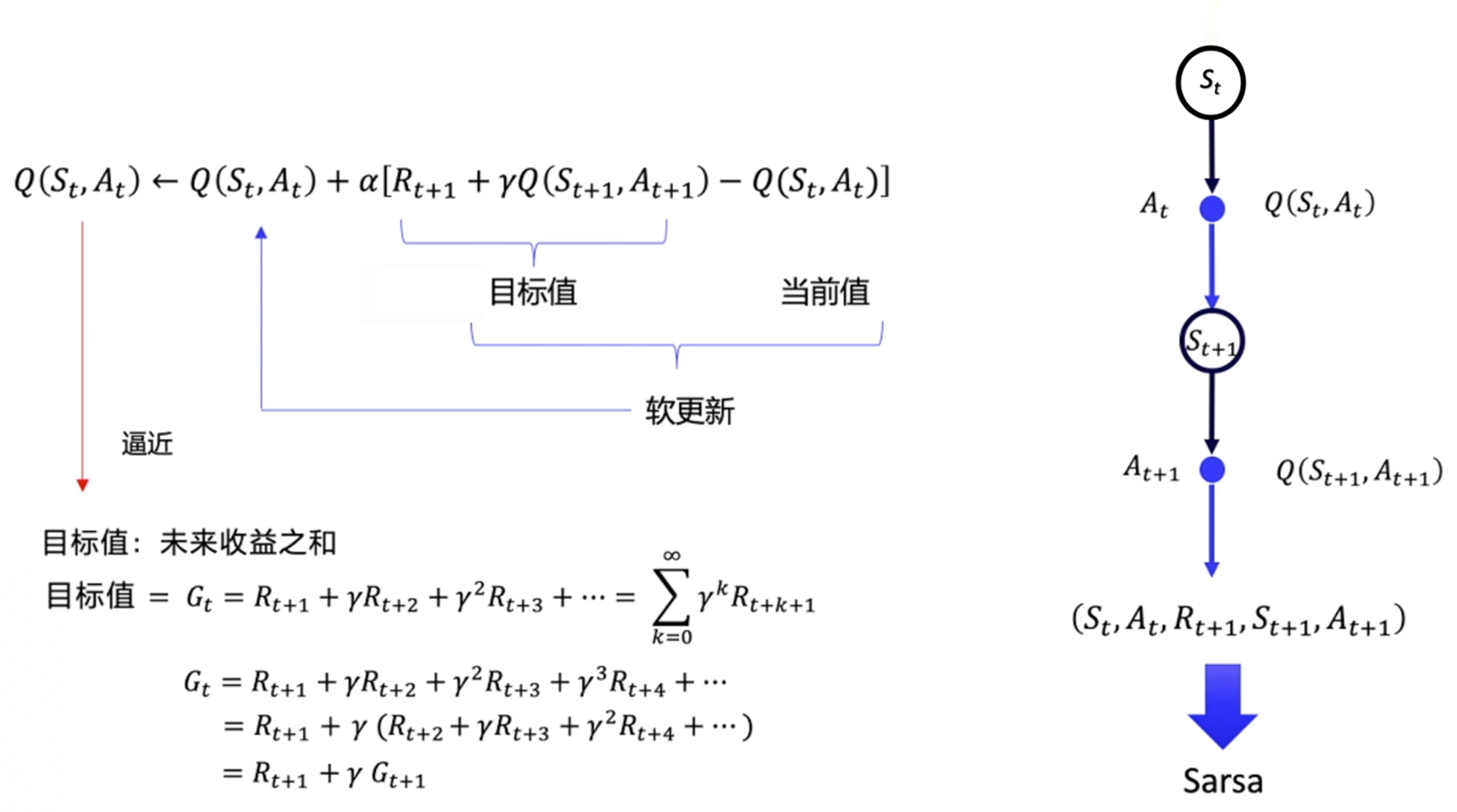
Sarsa 核心思想
核心思想
- 用时序差分方法来估计Q函数,更新Q表格后就可更新策略
- 用
下一步值, 来更新当前步值,不断强化每一个Q值
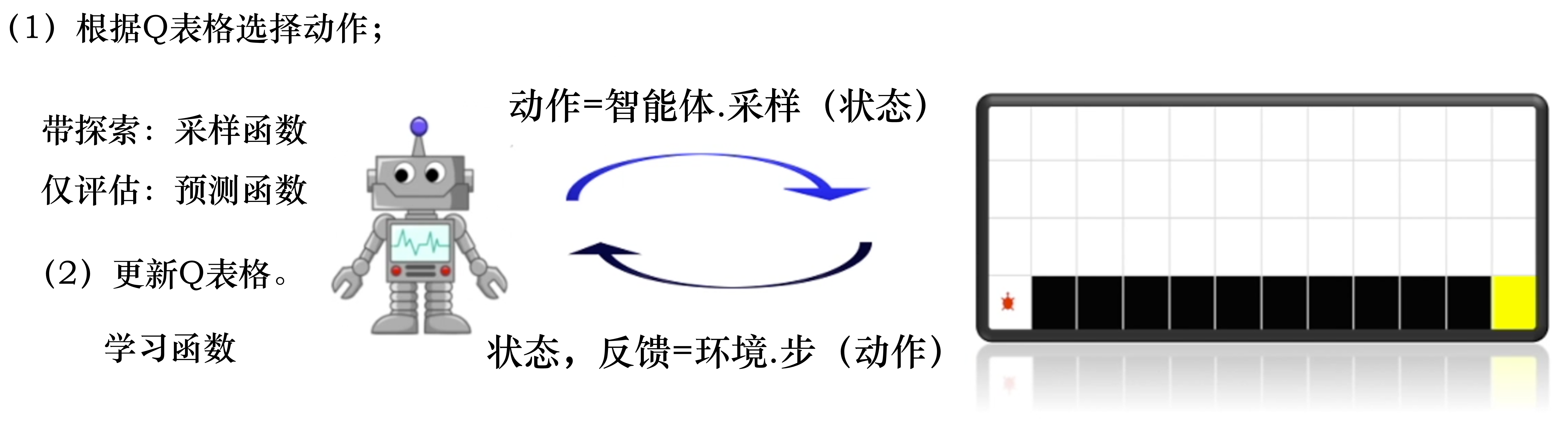
主要流程
随机初始化
,不断迭代直到 收敛,进行以下迭代 确定初始状态
,依策略选择动作 ,重复以下流程,直到 为终止态 环境交互采样
执行动作,得奖励 、新状态 - 在新状态
, 依策略选择动作
策略评估 / Q函数估计
策略改进 / 更新策略
状态动作前进:

n步Sarsa
单步时序差分
- 自举1步,用
下一步值, 来更新当前步值
n步时序差分
- 自举n步,一次性考虑
步回报
- n步回报
Sarsa(λ)
Q学习:异策略TD
核心思想
核心思想
同Sarsa一样,利用TD自举来估计Q函数,更新Q表格后可更新策略。
但
学习策略和行为策略不一样,是一种异策略算法学习策略
- 估计Q函数时,
采取下一时刻Q值最大的动作 , 不来自行为策略,并非下一步真正执行的动作学习策略动作和 行为策略动作不一样
- 估计Q函数时,
TD目标值:, 自举1步,更新Q函数
- 对比:Sarsa学习策略使用的动作
来自于行为策略采样的动作 , 二者相同
算法流程
初始化策略
,执行以下迭代,直到所有 收敛 初始化
,执行以下迭代,直到 为终止态 环境交互采样/探索策略
- 依策略选择动作
- 执行动作
,得即时奖励 、新状态
- 依策略选择动作
Q函数估计/学习策略
与sarsa不同,不使用探索策略
采样的、下一步真正执行的动作而是直接选择
最大Q值对应的动作用来估计Q。 , 不来自探索策略,并非下一步真正执行的动作
仅状态前进
策略更新,输出策略

伪代码
训练流程代码:多个回合
- agent采样动作:
agent.sample_action(state) - 环境交互:
env.step(action) - 样本放入经验池:
agent.meomory.push(xxx) - agent更新策略:
agent.update(xxx)
for i_ep in range(train_eps): # 遍历每个回合
# 重置环境,获取初始状态
state = env.reset() # 重置环境,即开始新的回合
while True: # 对于比较复杂的游戏可以设置每回合最大的步长,例如while ep_step<100,即最大步长为100。
# 智能体根据策略采样动作
action = agent.sample_action(state) # 根据算法采样一个动作
# 与环境进行一次交互,得到下一个状态和奖励
next_state, reward, terminated, _ = env.step(action) # 智能体将样本记录到经验池中
agent.memory.push(state, action, reward, next_state, terminated)
# 智能体更新策略
agent.update(state, action, reward, next_state, terminated)
# 更新状态
state = next_state
# 如果终止则本回合结束
if terminated:
breakAgent类:
- 采样动作:
贪心法,指数衰减 - 预测动作:直接根据
Q_table选择最大值即可 - 策略更新:
更新Q_table,
class Agent:
def __init__():
self.Q_table = defaultdict(lambda: np.zeros(n_actions))
def sample_action(self, state):
''' 采样动作,训练时用
'''
self.sample_count += 1
# epsilon是会递减的,这里选择指数递减
self.epsilon = self.epsilon_end + (self.epsilon_start - self.epsilon_end) * math.exp(- self.sample_count / self.epsilon_decay)
# e-greedy 策略
if np.random.uniform(0, 1) > self.epsilon:
action = np.argmax(self.Q_table[str(state)]) # 选择Q(s,a)最大对应的动作
else:
action = np.random.choice(self.n_actions) # 随机选择动作
return action
def predict_action(self,state):
''' 预测或选择动作,测试时用
'''
action = np.argmax(self.Q_table[str(state)])
return action
def update(self, state, action, reward, next_state, terminated):
''' 更新Q_table即可
'''
Q_predict = self.Q_table[str(state)][action]
if terminated: # 终止状态
Q_target = reward
else:
# TD目标计算,reward + 直接Q max值,而非给定下一时刻真正执行的动作的Q值
Q_target = reward + self.gamma * np.max(self.Q_table[str(next_state)])
self.Q_table[str(state)][action] += self.lr * (Q_target - Q_predict)
returnSarsa vs Q-Learning
Sarsa
- 同策略算法
- 自己的策略采样轨迹,并用
来更新
Q-Learning
- 异策略算法
- 不需要知道下一步实际执行哪个动作,更新Q时默认选择Q值最大的动作
- 不用知道下一步实际
,就能更新 - Q学习不担心受探索的影响,比Sarsa更大胆