有模型预测和控制
📅 发表于 2025/08/28
🔄 更新于 2025/08/28
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
rl theory
#有模型
#动态规划算法
#价值迭代
#策略迭代
#贝尔曼最优方程
#最优性原理
#价值函数
#最佳价值函数
#最佳策略函数
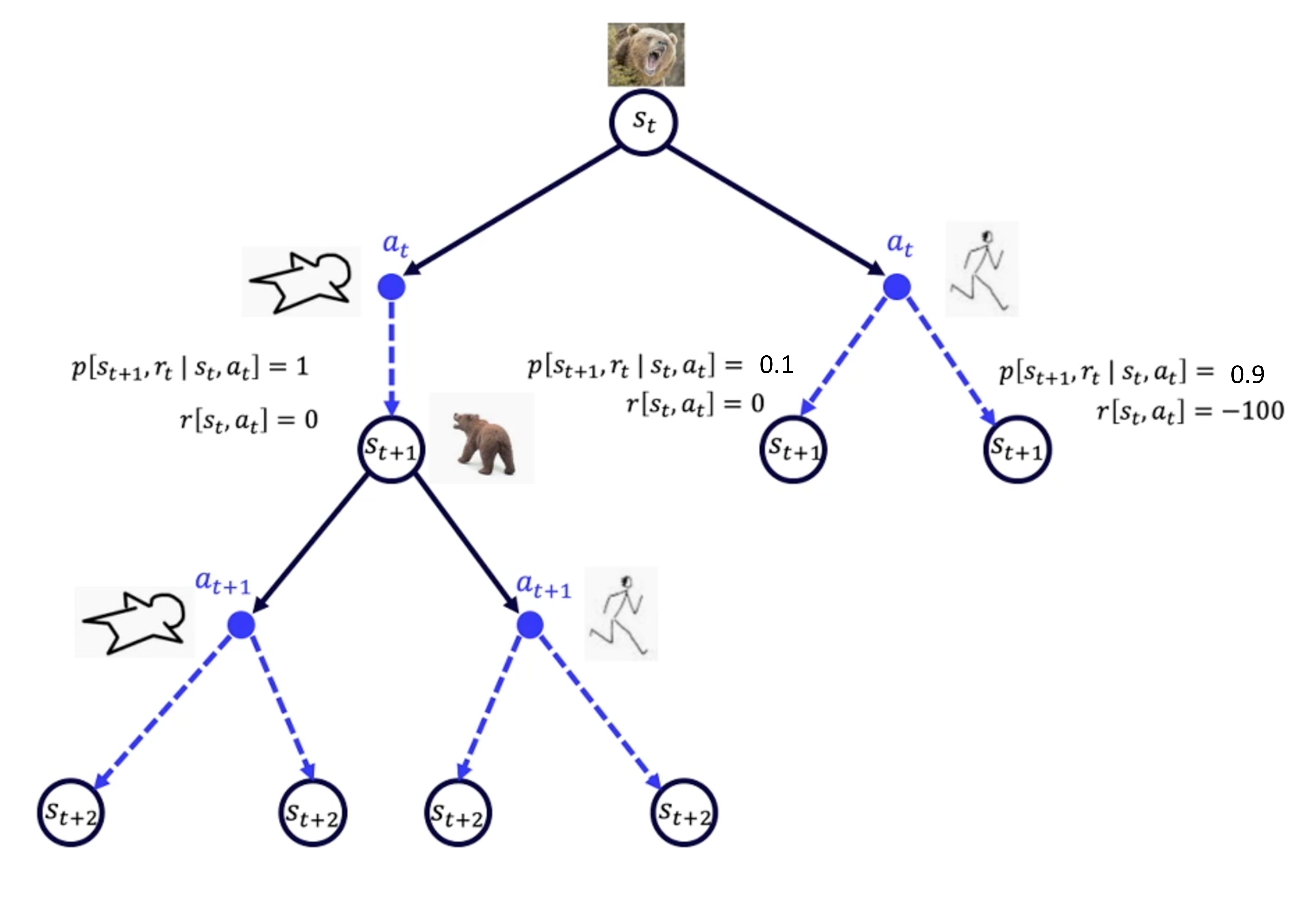
已知环境信息,状态转移概率和奖励函数,就变成一个状态转移序列决策问题。
但现实情况是,很难知道环境信息,压根不知道熊到底会做什么,一切都未知,需要免模型算法。
动态规划问题有如下3个特性
最优子结构/满足最优化原理
重叠子问题
无有效性
适用RL场景
核心思想
通过求解贝尔曼方程,来找到最优策略。当前状态的最优价值依赖于下一个状态的最有价值。用一个估计值去更新另一个估计值。 即时奖励+下一个状态的最优价值,保证当前最优决策是建立在后续最优决策基础上的。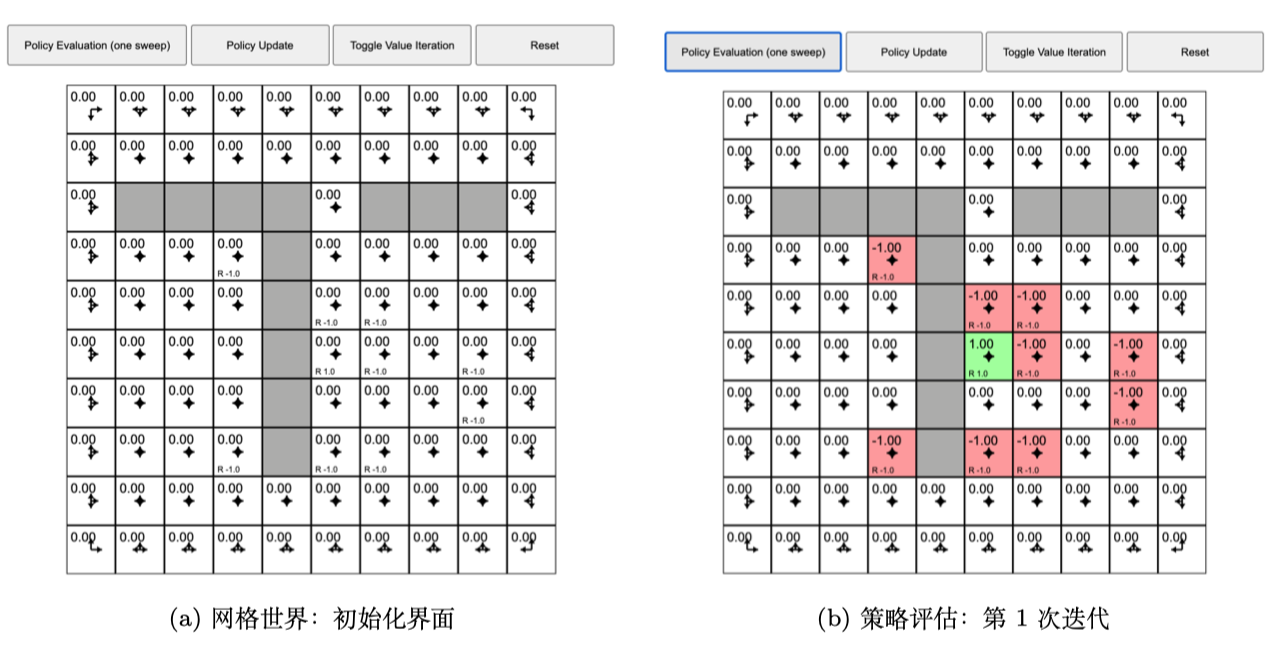
最佳价值函数和最佳策略
通过最佳价值函数来获取最佳策略
主要方法
核心思想
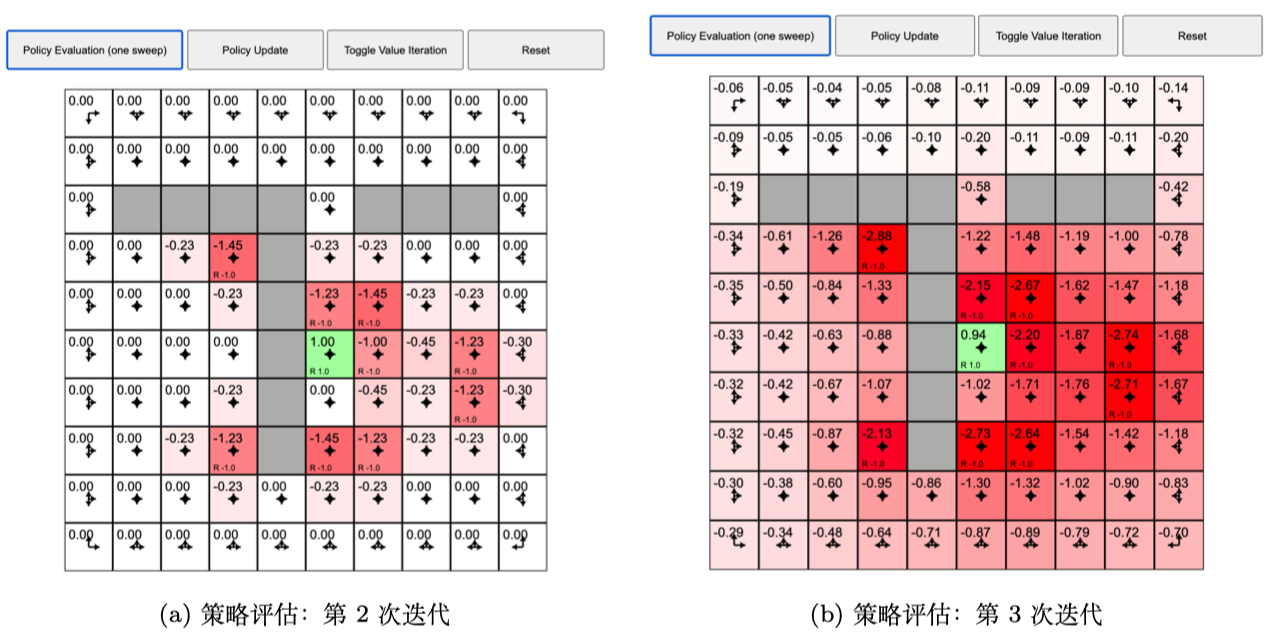
策略评估
策略改进
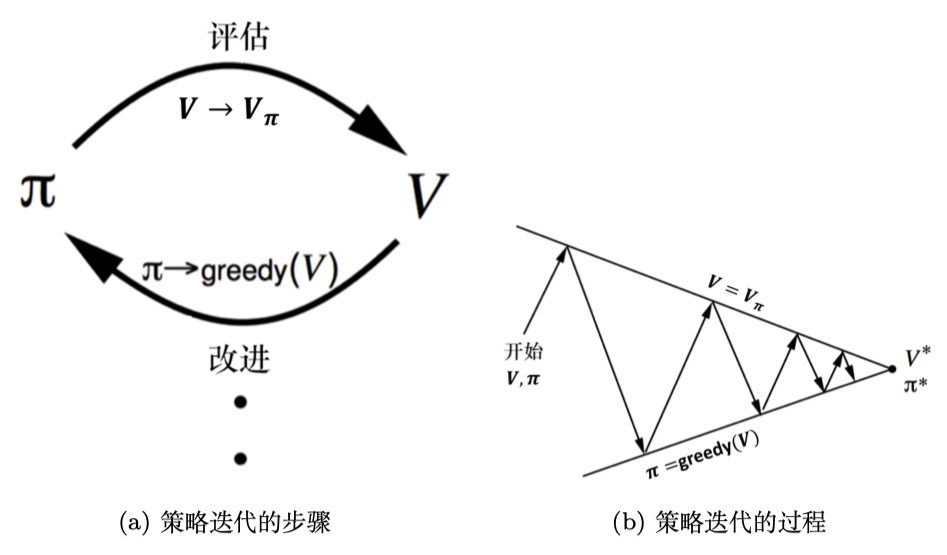
策略改进结束后
Q函数贝尔曼最优方程
V函数贝尔曼最优方程
由动态规划策略评估可知
最优性原理
核心思想
贝尔曼最优方程来迭代计算关键流程
所有状态初始化:
从k=1迭代到H次,每次迭代如下:
迭代完成后,提取最优策略