基于策略函数的学习方法

背景

强化学习目标

基于策略函数的学习方法

• 无需值函数直接优化策略，参数化的策略处理可以处理连续状态和动作
• 基于梯度的学习、无梯度的学习

策略梯度

策略梯度概览

1. 核心思想

• 假设策略${\pi }_{\theta }(a\mid s)$是一个关于$\theta$的连续可微函数 (策略连续可微假设)
• 用梯度上升的方法优化参数$\theta$使目标函数$J(\theta )$最大。 策略梯度是一种基于梯度的RL方法。

$$J(\theta )=\int p_{\theta }(\tau )\cdot G(\tau )\mathrm{d}\tau$$

2. 总结核心3个推导步骤

• 代入$J(\theta )$目标函数，算导数

$$\frac{\partial J(\theta )}{\partial \theta }\triangleq E_{\tau \sim p_{\theta }(\tau )}\left[\frac{\partial }{\partial \theta }\log p_{\theta }(\tau )\cdot G(\tau )\right]$$

• 代入策略$\pi$和状态转移概率$p(s_{t+1}|s_t,a_a)$，细分偏导数

$$\frac{\partial }{\partial \theta }\log p_{\theta }(\tau )=\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)$$

• 代入轨迹回报$G(\tau )$做分解，算出策略梯度 ⭐

$$\begin{array}{rl}\frac{\partial J(\theta )}{\partial \theta }& =E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t=0}^{T-1}\left(\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot {\gamma }^{t}G({\tau }_{t:T})\right)\right]\end{array}$$

策略梯度详细推导过程

策略梯度推导 (目标函数$J(\theta )$关于策略参数$\theta$的导数推导)

• 代入$J(\theta )$，求导数转换成期望形式
  • 参数$\theta$的优化方向：使总回报越大的轨迹$\tau$概率也越大, $G(\tau )\uparrow \Rightarrow p_{\theta }(\tau )\uparrow$

$$\begin{array}{ll}\frac{\partial J(\theta )}{\partial \theta }& =\frac{\partial }{\partial \theta }\int p_{\theta }(\tau )G(\tau )\mathrm{d}\tau \\ & =\int (\frac{\partial }{\partial \theta }{p}_{\theta }(\tau ))\cdot G(\tau )\mathrm{d}\tau \\ & =\int \underset{\mathrm{梯}\mathrm{度}\mathrm{写}\mathrm{成}\mathrm{期}\mathrm{望}\mathrm{形}\mathrm{式}，\mathrm{便}\mathrm{于}\mathrm{蒙}\mathrm{特}\mathrm{卡}\mathrm{罗}\mathrm{估}\mathrm{计}}{\underbrace{p_{\theta }(\tau )\cdot (\frac{1}{p_{\theta }(\tau )}\cdot \frac{\partial p_{\theta }(\tau )}{\partial \theta })\cdot G(\tau )\mathrm{d}\tau }}\\ & =\int p_{\theta }(\tau )\cdot \underset{\mathrm{对}\mathrm{数}\mathrm{恒}\mathrm{等}\mathrm{式}}{\underbrace{(\frac{\partial }{\partial \theta }\log p_{\theta }(\tau ))}}\cdot G(\tau )d\tau \\ & =E_{\tau \sim p_{\theta }(\tau )}\left[\frac{\partial }{\partial \theta }\log p_{\theta }(\tau )\cdot G(\tau )\right]\end{array}$$$$\begin{array}{ll}\mathrm{导}\mathrm{数}：& f(x)=\log (x),f^{\prime }(x)=\frac{1}{x}\\ \mathrm{对}\mathrm{数}\mathrm{恒}\mathrm{等}\mathrm{式}：& \frac{\partial }{\partial \theta }\log f(\theta )=\frac{1}{f(\theta )}\cdot \frac{\partial f(\theta )}{\partial \theta }\end{array}$$

• 代入策略$\pi$和环境状态转移概率$p(s_{t+1}\mid s_t,a_t)$，进一步细分偏导数，梯度只和策略相关

  $$\begin{array}{ll}\frac{\partial }{\partial \theta }\log p_{\theta }(\tau )& =\frac{\partial }{\partial \theta }\log (\underset{\mathrm{初}\mathrm{始}\mathrm{状}\mathrm{态}}{\underbrace{p(s_0)}}\cdot \prod _{t=0}^{T-1}\underset{\mathrm{执}\mathrm{行}\mathrm{动}\mathrm{作}}{\underbrace{{\pi }_{\theta }(a_t\mid s_t)}}\cdot \underset{\mathrm{状}\mathrm{态}\mathrm{改}\mathrm{变}}{\underbrace{p(s_{t+1}\mid s_t,a_t)}})\\ & =\frac{\partial }{\partial \theta }(\underset{\theta \mathrm{求}\mathrm{导}\mathrm{为}0}{\underbrace{\log p(s_0)}}+\sum _{t=0}^{T-1}\log {\pi }_{\theta }(a_t\mid s_t)+\underset{\theta \mathrm{求}\mathrm{导}\mathrm{为}0}{\underbrace{\sum _{t=0}^{T-1}\log p(s_{t+1}\mid s_t,a_t)}})\\ & =\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\end{array}$$

• 代入$G(\tau )$分解回报，算出策略梯度

$$\begin{array}{ll}\frac{\partial J(\theta )}{\partial \theta }& =E_{\tau \sim p_{\theta }(\tau )}\left[\frac{\partial }{\partial \theta }\log p_{\theta }(\tau )\cdot G(\tau )\right]\\ & =E_{\tau \sim p_{\theta }(\tau )}[\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot G(\tau )]\\ & =E_{\tau \sim p_{\theta }(\tau )}[\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot (\underset{r_0\sim r_{t-1}}{\underbrace{G({\tau }_{0:t})}}+\underset{r_t\sim r_T}{\underbrace{{\gamma }^t\cdot G({\tau }_{t:T})}})]\\ & =E_{\tau \sim p_{\theta }(\tau )}[\underset{\mathrm{为}0，a_t\mathrm{只}\mathrm{影}\mathrm{响}\mathrm{后}\mathrm{面}，\mathrm{不}\mathrm{贡}\mathrm{献}\mathrm{梯}\mathrm{度}}{\underbrace{\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot G({\tau }_{0:t})}}+\underset{\mathrm{不}\mathrm{为}0}{\underbrace{\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot G({\tau }_{t:T})}}]\\ & =E_{\tau \sim p_{\theta }(\tau )}\left[\sum _{t=0}^{T-1}\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t\mid s_t)\cdot {\gamma }^t\cdot G({\tau }_{t:T})\right]\end{array}$$

• 其中 $G(\tau )$分解为2部分 ：0-t的累计回报 和 t到T的累计回报，
  • 注意：时刻t的动作$a_t$ 只能影响t时刻之后的奖励，不能影响t时刻之前的奖励。

$$G(\tau )=\sum _{t=0}^{T-1}{\gamma }^t\cdot r_{t+1}=G({\tau }_{0:t})+{\gamma }^t\cdot G({\tau }_{t:T})$$

• $G({\tau }_{t:T})$：时刻t作为起始时刻到时刻T，收到的总回报

$$G({\tau }_{t:T})=\sum _{k=t}^{T-1}{\gamma }^{k-t}\cdot r_{k+1}$$

REINFORCE算法

REINFORCE

核心思想

• 策略梯度中，通过当前策略${\pi }_{\theta }$随机采样N条轨迹来近似期望。${\tau }^{(1)},\cdots ,{\tau }^{(N)}$

$$\begin{array}{ll}\frac{\partial J(\theta )}{\partial \theta }& \approx \frac{1}{N}\sum _{n=1}^N\left(\sum _{t=0}^{T-1}\underset{\mathrm{每}\mathrm{个}\mathrm{时}\mathrm{刻}\mathrm{的}\mathrm{策}\mathrm{略}\mathrm{梯}\mathrm{度}}{\underbrace{\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t^{(n)}|s_t^{(n)})\cdot {\gamma }^{t}G({\tau }_{t:T}^{(n)})}}\right)\end{array}$$

• 结合随机梯度上升算法，每次采样1条轨迹，并计算每个时刻的梯度，来更新参数

算法步骤

• 输入：状态空间$\mathcal{S}$，动作空间$\mathcal{A}$，可微分策略函数${\pi }_{\theta }(a\mid s)$，折扣率$\gamma$，学习率$\alpha$

• 初始化：随机初始化参数$\theta$，训练直到收敛

• 根据${\pi }_{\theta }(a\mid s)$采样一条轨迹

$$\tau =s_0,a_0,s_1,a_1,\cdots ,s_{T-1},a_{T-1},s_T$$

• 在每个时刻计算回报$G({\tau }_{t:T})$、策略梯度，并更新策略函数参数 (0~T)

$$\theta \leftarrow \theta +\alpha \cdot \underset{\mathrm{每}\mathrm{个}\mathrm{时}\mathrm{刻}\mathrm{的}\mathrm{策}\mathrm{略}\mathrm{梯}\mathrm{度}}{\underbrace{\frac{\partial }{\partial \theta }\log {\pi }_{\theta }(a_t|s_t)\cdot {\gamma }^{T}G({\tau }_{t:T})}}$$

缺点

• 不同路径的方差很大，导致训练不稳定；
• 需要根据一个策略采集一条完整的轨迹。

带基准线的REINFORCE算法

带基准线的REINFORCE 算法思想

背景

• REINFORCE缺点：不同轨迹样本$G(\tau )$方差很大，导致训练不稳定

核心思想

• 使用基准函数$b(s_t)$去减小策略梯度的方差，基准函数和$a_t$无关

  • 准确是减少$G(\tau )$带来的方差。

• 每个时刻的策略梯度：引入基准函数之前

$$\begin{array}{ll}\frac{\partial J_t(\theta )}{\partial \theta }& =E_{s_t,a_t}[\frac{\partial }{\partial \theta }\log \pi (a_t\mid s_t)\cdot {\gamma }^{t}G({\tau }_{t:T})]\\ & =E_{s_t,a_t}[{\mathrm{\nabla }}_{\theta }\log \pi (a_t\mid s_t)\cdot {\gamma }^{t}G({\tau }_{t:T})]\end{array}$$

• 每个时刻的策略梯度：引入基准函数之后

$$\frac{\partial {\hat{J}}_t(\theta )}{\partial \theta }=E_{s_t,a_t}[\frac{\partial }{\partial \theta }\log \pi (a_t\mid s_t)\cdot {\gamma }^t\underset{\mathrm{基}\mathrm{准}\mathrm{函}\mathrm{数}，\mathrm{减}\mathrm{小}G\mathrm{方}\mathrm{差}}{\underbrace{(G({\tau }_{t:T})-b(s_t))}}]$$

• 由于 $b(s_t)$和$a_t$无关 ，通过推导可知新旧策略梯度一致，保证了无偏性

$$\frac{\partial \hat{J}(\theta )}{\partial \theta }=\frac{\partial J(\theta )}{\partial \theta }$$

• 由下文降低方差的方法推导可知：$b(s_t)$和$G({\tau }_{t:T})$ 越相关，方差越小，就越好

基准函数的选择

• 很自然可以选择值函数作为基准函数 ：$b(s_t)=V^{{\pi }_{\theta }}(s_t)$。

• 但由于值函数未知，可用学习参数$V_{\varphi }(s_t)$来近似值函数

• 用参数估计，目标函数如下，和Q网络参数逼近很像。

  $$\mathcal{L}(\varphi \mid s_t,{\pi }_{\theta })=(V^{{\pi }_{\theta }}(s_t)-V_{\varphi }(s_t){)}^2$$

• 用蒙特卡罗来估计$V^{{\pi }_{\theta }}(s_t)$

• 最终策略函数参数$\theta$的梯度如下

$$\frac{\partial {\hat{J}}_t(\theta )}{\partial \theta }=E_{s_t,a_t}[\frac{\partial }{\partial \theta }\log \pi (a_t\mid s_t)\cdot {\gamma }^t\underset{\mathrm{基}\mathrm{准}\mathrm{函}\mathrm{数}，\mathrm{减}\mathrm{小}G\mathrm{方}\mathrm{差}}{\underbrace{(G({\tau }_{t:T})-V_{\varphi }(s_t))}}]$$

带基准线REINFORCE算法步骤

算法步骤

• 输入：状态空间$\mathcal{S}$，动作空间$\mathcal{A}$，可微分策略函数${\pi }_{\theta }(a\mid s)$，可微分状态值函数$V_{\varphi }(s)$，折扣率$\gamma$，学习率$\alpha$
• 初始化：随机初始化参数$\theta 、\varphi$，训练直到策略收敛，输出${\pi }_{\theta }$
• 根据策略${\pi }_{\theta }(a|s)$生成1条轨迹，

$$\tau =s_0,a_0,s_1,a_1,\cdots ,s_{T-1},a_{T-1},s_T$$

• 每个时刻循环计算，先计算$G({\tau }_{t:T})$，再依次更新值函数和策略函数参数

$$\begin{array}{l}\delta \leftarrow G({\tau }_{t:T})-V_{\varphi }(s_t)\\ \varphi \leftarrow \varphi +\beta \cdot \delta \cdot \frac{\partial }{\partial \varphi }{V}_{\varphi }(s_t)\\ \theta \leftarrow \theta +\alpha \cdot {\gamma }^t\delta \cdot \frac{\partial }{\partial \theta }\log \pi (a_t|s_t)\end{array}$$

降低方差方法的公式推导

目的

• 估计$E[f]$，构造新估计量$\hat{f}$，使得
  • 无偏性：$E[f]=E[\hat{f}]$，
  • 减小方差：$Var(\hat{f})<Var(f)$

核心方法

• 构建$\hat{f}$：引入一个与f相关的辅助函数g，E[g]已知。

$$\hat{f}=f-\alpha (g-E[g])$$

• 保证无偏性推导期望：推导可知$E[\hat{f}]=E[f]$

$$E[\hat{f}]=E[f]-\alpha \cdot E(g-E[g])=E[f]-\alpha \cdot (E[g]-E[g])=E[f]$$

• 推导方差供减小优化使用$\mathrm{Var}(\hat{f})$： 方差、协方差

$$\begin{array}{ll}Var(\hat{f})& =\mathrm{Var}(f-\alpha (g-E[g]))\\ & =\mathrm{Var}(f-\alpha \cdot g)\\ & =\mathrm{Var}(f)+{\alpha }^2\mathrm{Var}(g)-2\alpha \cdot \mathrm{Cov}(f,g)\end{array}$$

• 最小方差求解：求解极值点 $\alpha$取值
  • 方差恒为正，是常数；根据上式可知$Var(\hat{f})$是关于$\alpha$的凹函数，必然存在极小值
  • 求导数并使其为0，求解出最小值时的取值。

$$\begin{array}{l}\frac{\partial Var(\hat{f})}{\partial \alpha }=2\alpha Var(g)-2Cov(f,g)\\ \mathrm{令}\mathrm{其}=0，\mathrm{得}:\alpha =\frac{Cov(f,g)}{Var(g)}\end{array}$$

• 最小方差求解：代回极值点，求解出最小值

$$\begin{array}{ll}Var(\hat{f})& =Var(f)+\frac{Co{v}^2(f,g)}{Var(g)}-2\frac{Co{v}^2(f,g)}{Var(g)}\\ & =Var(f)-\frac{Co{v}^2(f,g)}{Var(g)}\\ & =Var(f)(1-\frac{Co{v}^2(f,g)}{Var(f)Var(g)})\\ & =Var(f)\cdot (1-\underset{\mathrm{相}\mathrm{关}\mathrm{系}\mathrm{数}}{\underbrace{{\rho }^2(f,g))}})\end{array}$$

• 极小值：$f$和$g$的相关性越高，$Var(\hat{f})$越小

Actor-Critic算法

Actor-Critic 算法

背景

• REINFORCE算法 方差大、学习效率较低，$G({\tau }_{t:T})$ 计算慢
  • 每次根据一个策略采样一条完整轨迹，并计算这条轨迹上的回报
• 借TD动态规划思想，提高采样效率，状态s的总回报由即时奖励和下个状态的值函数来估计。

核心思想

• 迭代计算t作为初始时刻的轨迹总回报 $G({\tau }_{t:T})$

$$\hat{G}({\tau }_{t:T})=r_{t+1}+\gamma V_{\varphi }(s_{t+1})$$

• 初始，演员随机表演、评论员随机打分；通过每步各自不断学习更新，评分越来越准、表演越来越好。
  • 演员，策略函数${\pi }_{\theta }(s,a)$：学习策略获得高回报
  • 评论员，值函数$V_{\varphi }(s)$，评估当前策略好坏
• $V_{\varphi }(s)$值函数目标函数，调整打分标准

$$\mathcal{L}(\varphi )=\underset{\varphi }{min}(\hat{G}({\tau }_{t:T})-V_{\varphi }(s){)}^2=\underset{\varphi }{min}(\underset{\mathrm{动}\mathrm{态}\mathrm{规}\mathrm{划},\mathrm{实}\mathrm{际}\mathrm{值}}{\underbrace{r_{t+1}+\gamma V_{\varphi }(s_{t+1})}}-\underset{\mathrm{预}\mathrm{测}\mathrm{值}}{\underbrace{V_{\varphi }(s_t)}}{)}^2$$

• ${\pi }_{\theta }(s,a)$策略函数策略梯度， 调整策略；值函数作为基线函数，降低方差，

$$\frac{\partial {\hat{J}}_t(\theta )}{\partial \theta }=E_{s_t,a_t}[\frac{\partial }{\partial \theta }\log \pi (a_t\mid s_t)\cdot {\gamma }^t\underset{\mathrm{基}\mathrm{准}\mathrm{函}\mathrm{数}，\mathrm{减}\mathrm{小}G\mathrm{方}\mathrm{差}}{\underbrace{(\hat{G}({\tau }_{t:T})-V_{\varphi }(s_t))}}]$$

• 值函数3个功能
  • 估计轨迹真实回报（打分）
  • 更新值函数参数$\varphi$ （调整打分标准）
  • 作为基函数来减少策略梯度的方差（调整策略）

优点

• 可以单步更新参数，不需要等到回合结束才进行更新

Actor-Critic 算法步骤

算法步骤

• 输入：状态空间$\mathcal{S}$，动作空间$\mathcal{A}$，可微分策略函数${\pi }_{\theta }(a\mid s)$，可微分状态值函数$V_{\varphi }(s)$，折扣率$\gamma$，学习率$\alpha 、\beta$
• 初始化：随机初始化参数$\theta 、\varphi$，训练直到策略收敛，输出${\pi }_{\theta }$
• 初始化起始状态s，每个步骤做采样更新，直到s为终止态
• 执行动作 $a={\pi }_{\theta }(a|s)$，获得奖励 $r(s,a,s^{\prime })$和新状态$s^{\prime }$
• 动态规划估计轨迹回报，计算基准差值 $\delta$，更新值函数参数、更新策略函数参数

$$\begin{array}{ll}\mathrm{预}\mathrm{估}\mathrm{轨}\mathrm{迹}\mathrm{回}\mathrm{报}& G({\tau }_{t:T})\leftarrow r+\gamma V_{\varphi }(s^{\prime })\\ \mathrm{基}\mathrm{准}\mathrm{函}\mathrm{数}\mathrm{差}\mathrm{值}& \delta \leftarrow G({\tau }_{t:T})-V_{\varphi }(s)=r+\gamma V_{\varphi }(s^{\prime })-V_{\varphi }(s)\\ \mathrm{值}\mathrm{函}\mathrm{数}\mathrm{参}\mathrm{数}& \varphi \leftarrow \varphi +\beta \cdot \delta \cdot \frac{\partial }{\partial \varphi }{V}_{\varphi }(s_t)\\ \mathrm{策}\mathrm{略}\mathrm{函}\mathrm{数}\mathrm{参}\mathrm{数}& \theta \leftarrow \theta +\alpha \cdot {\gamma }^t\delta \cdot \frac{\partial }{\partial \theta }\log \pi (a_t|s_t)\end{array}$$

强化学习算法总结

方法总览

1. 通用步骤

1. 执行策略，生成样本
2. 估计回报
3. 更新策略

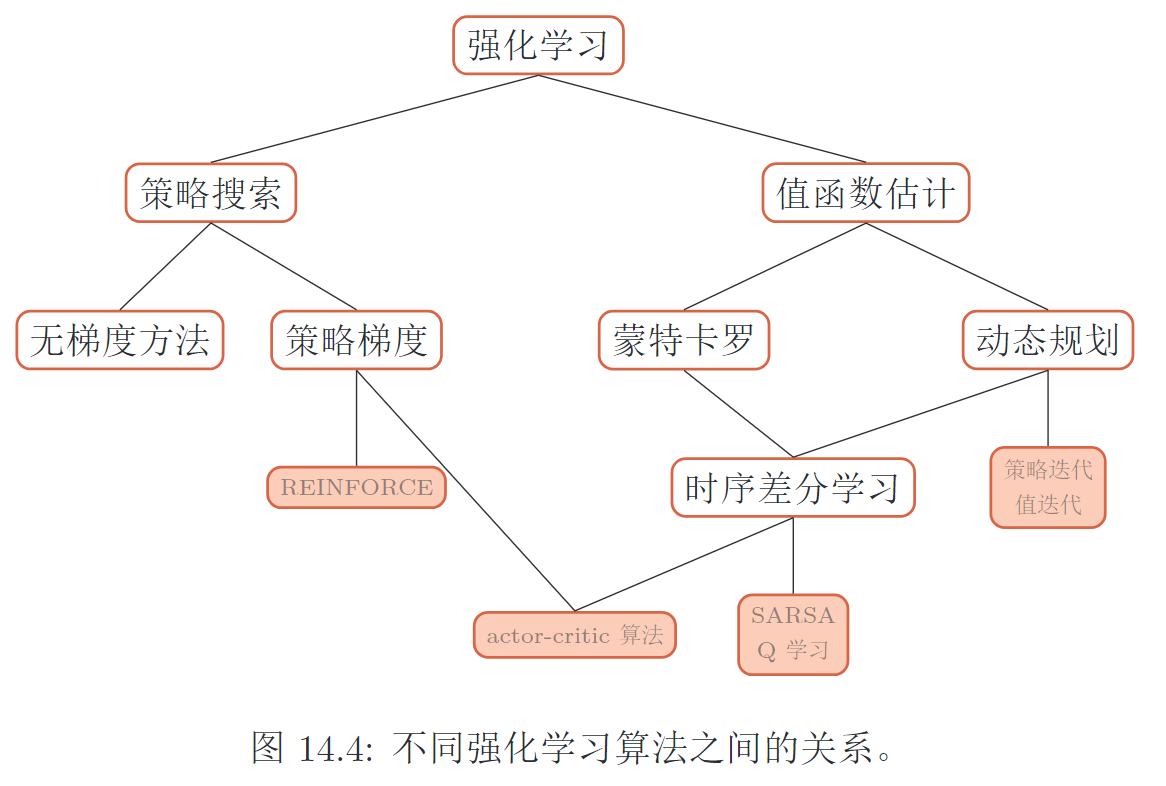
2. 值函数与策略函数的比较

值函数的方法

策略更新，导致值函数的改变比较大，对收敛性有一定的影响

策略函数的方法

策略更新，更加平稳。

缺点：策略函数的解空间很大，难以进行充分采样，导致方差较大，容易陷入局部最优解。

四个典型方法

与监督学习的区别

	强化学习	监督学习
样本	与环境进行交互产生样本，进行试错学习	人工收集并标注
反馈	只有奖励，并且是延迟的	需要明确的指导信息（每个状态对应一个动作）