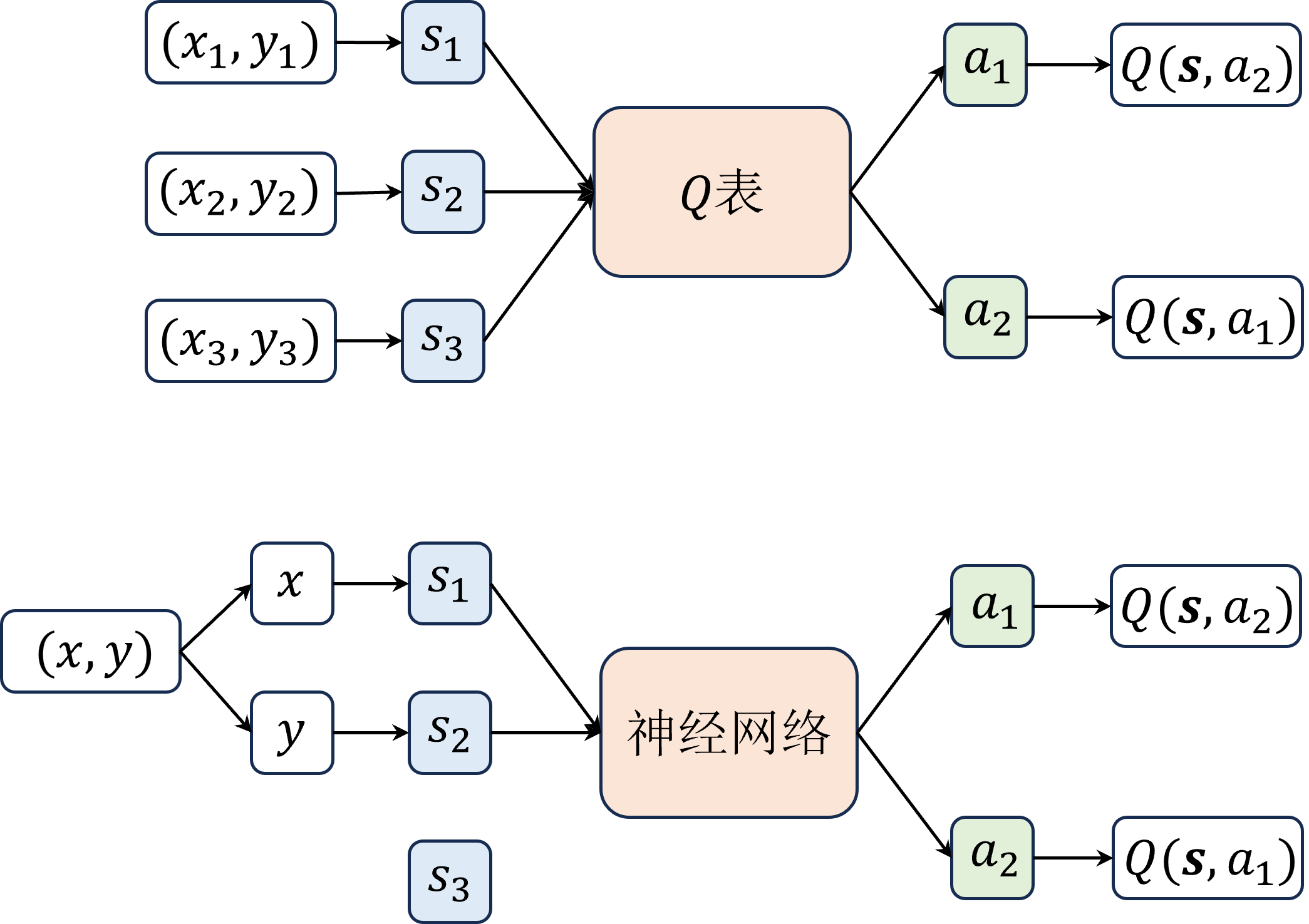
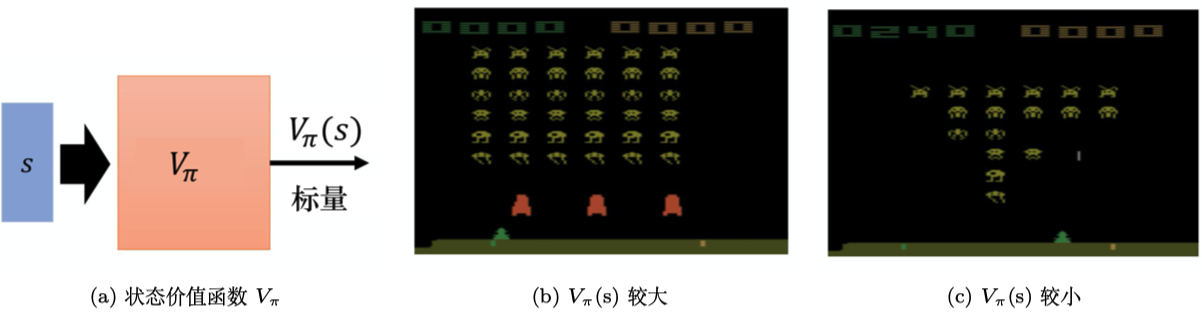
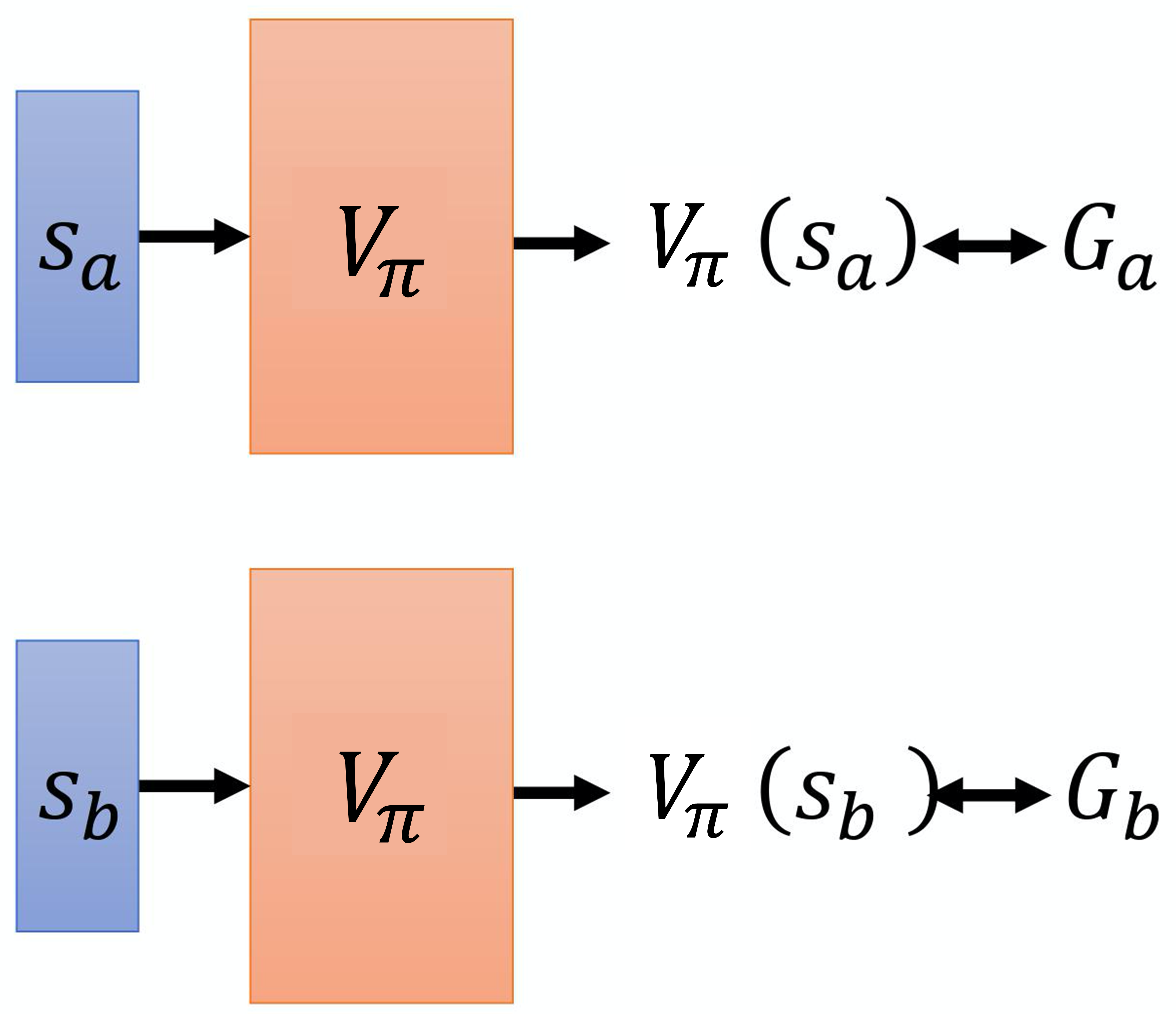
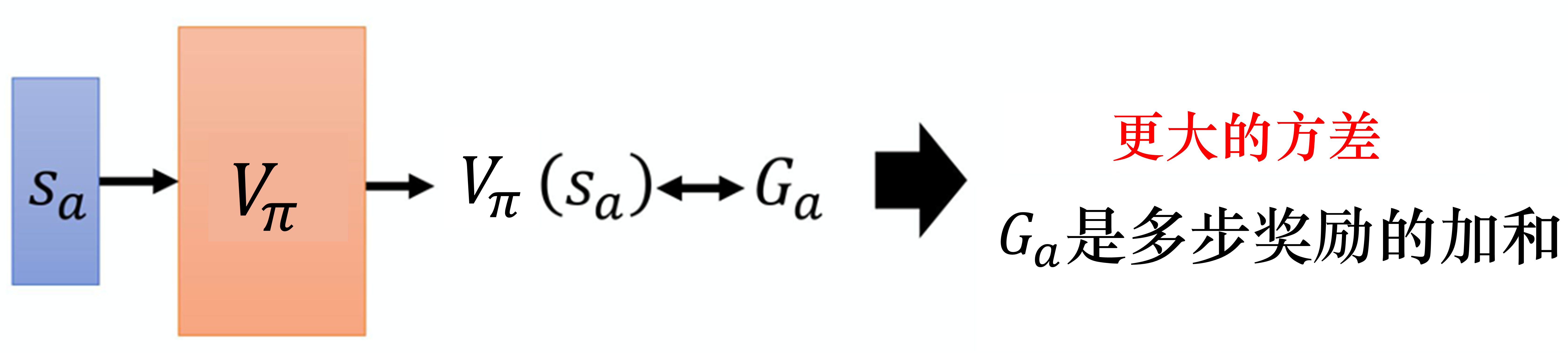
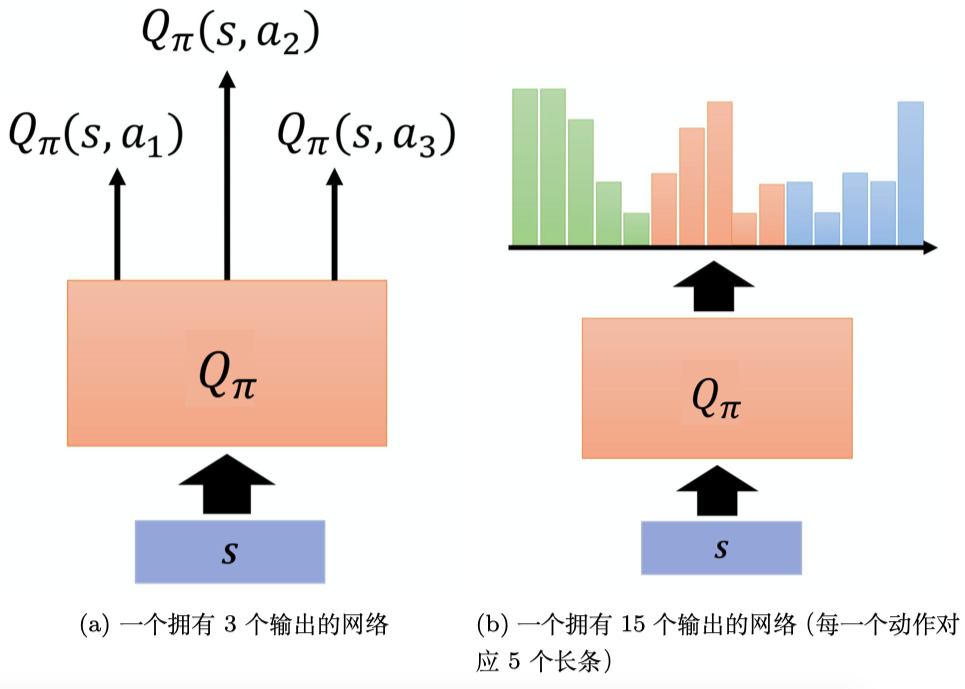
DQN算法及进阶
📅 发表于 2025/08/29
🔄 更新于 2025/08/29
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
rl-theory
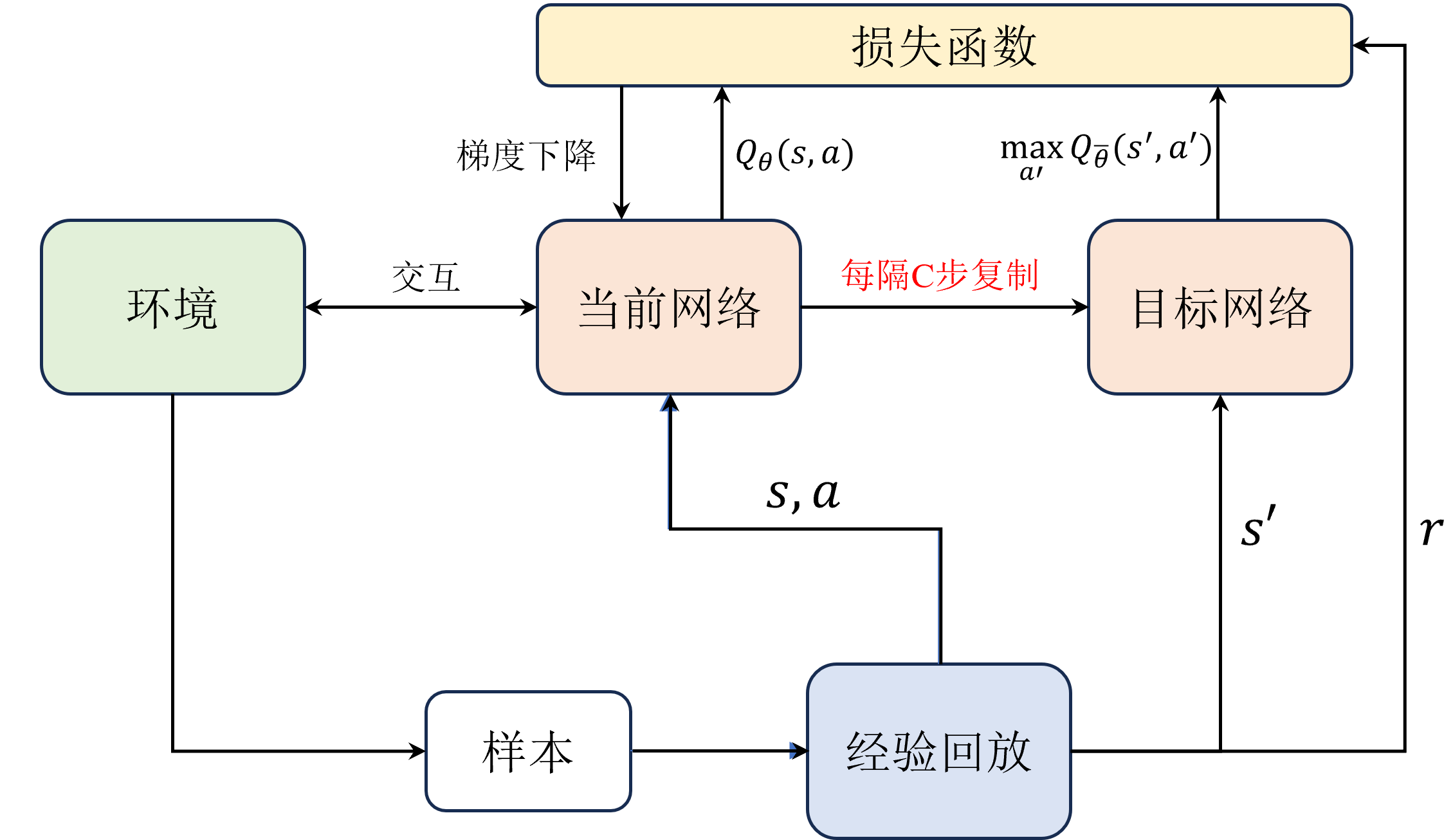
#DQN
#Q网络
#半梯度方法
#致命三元组
#目标值
#预测值
#MSE Loss
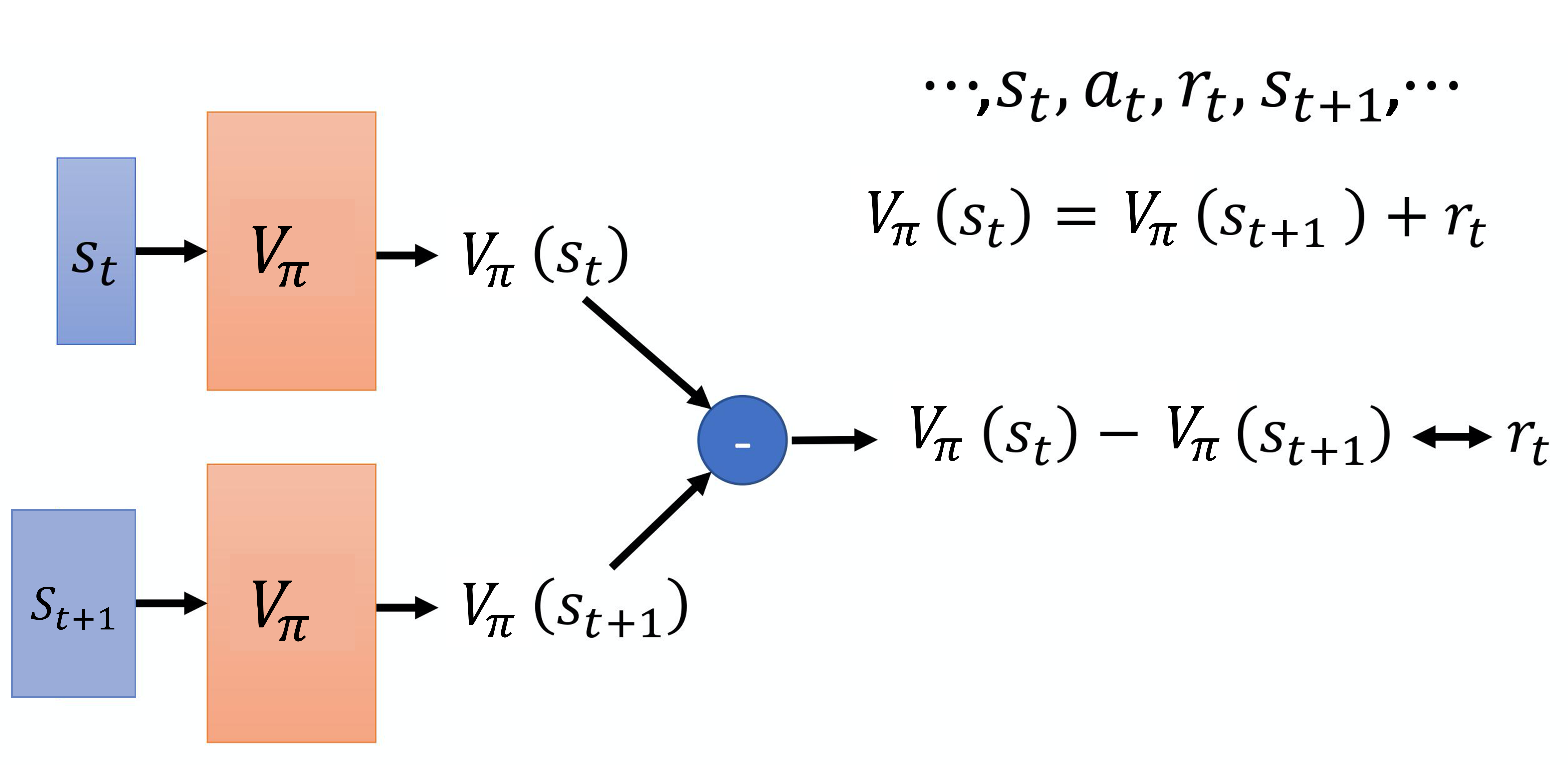
#评论员
#评论员V函数
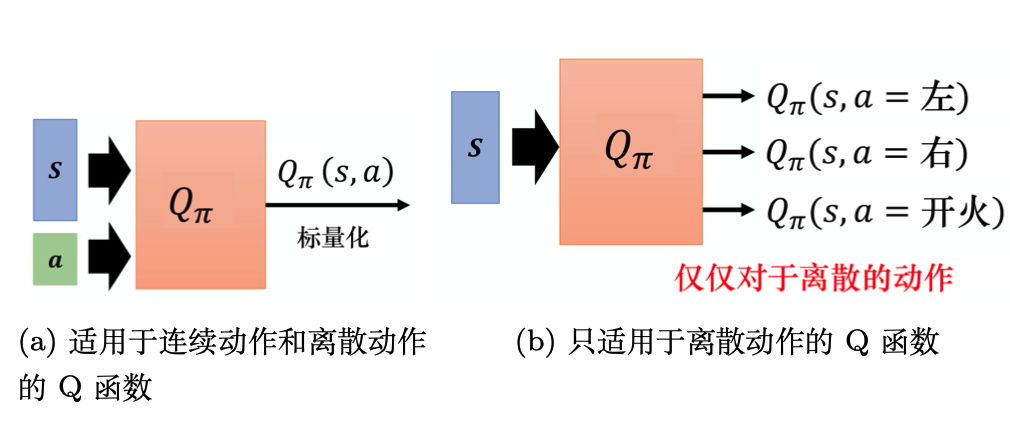
#评论员Q函数
#蒙特卡洛
#时序差分
#对比Case
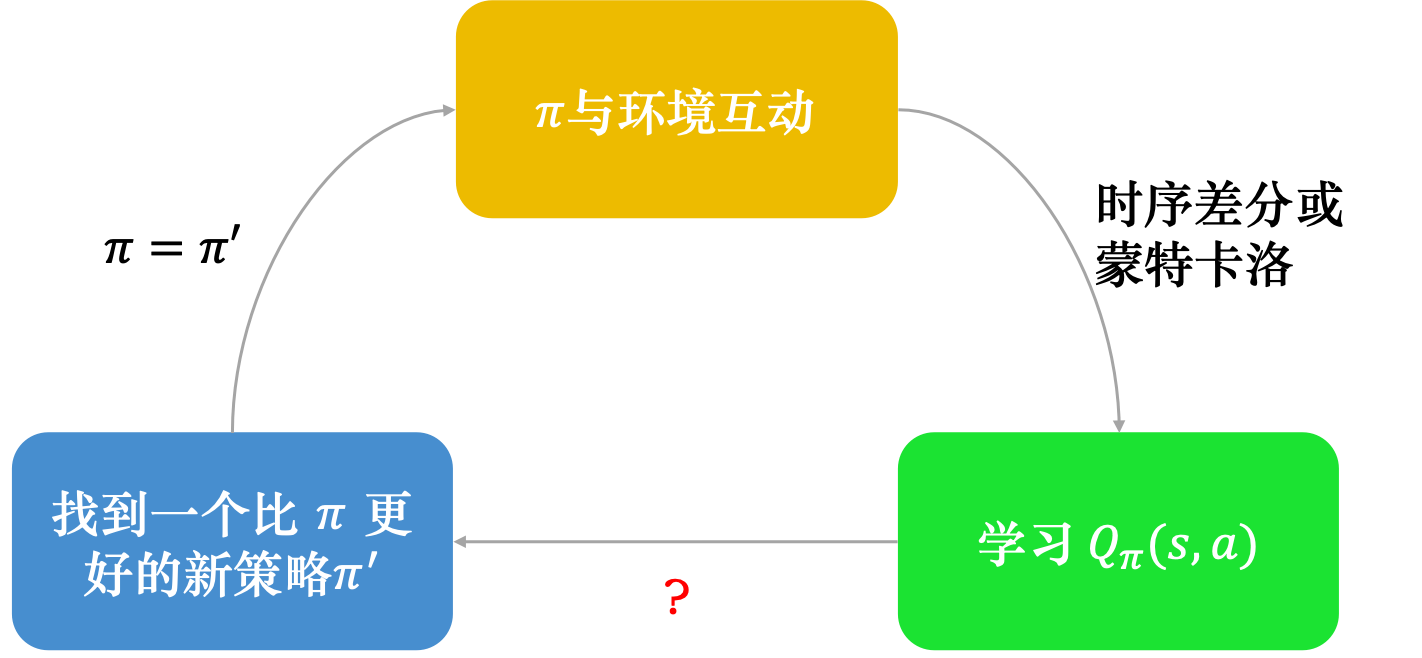
#Q函数学习过程
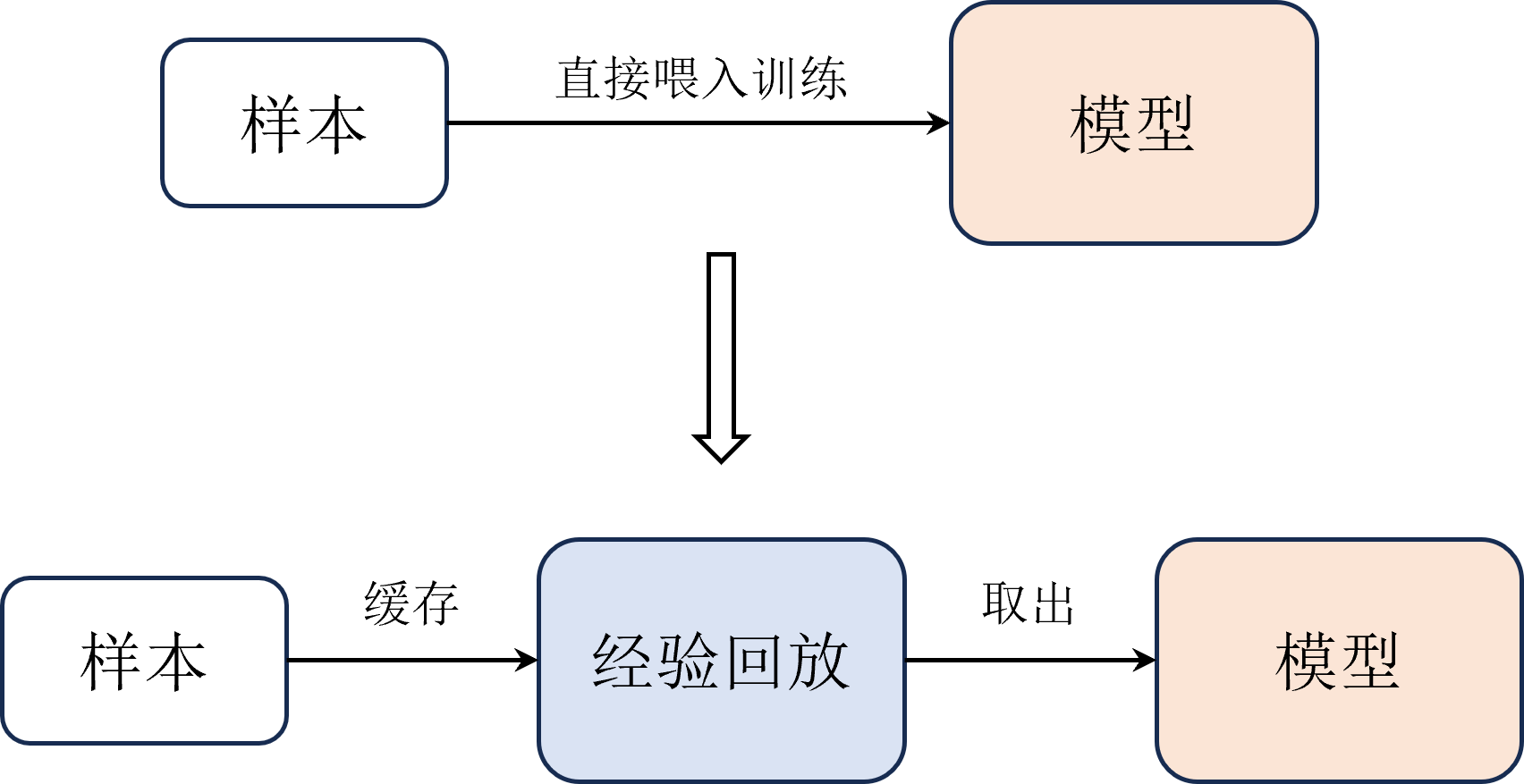
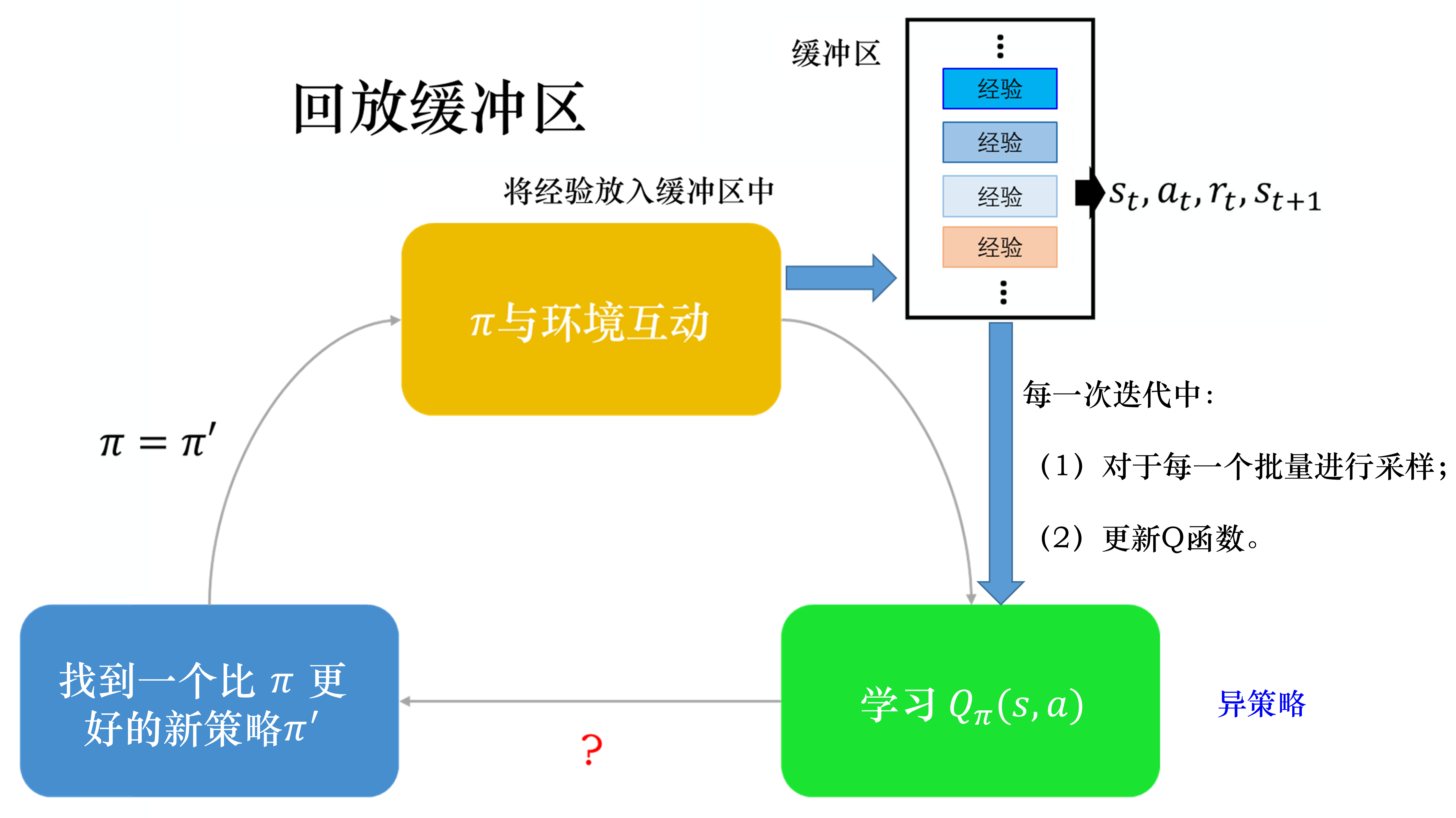
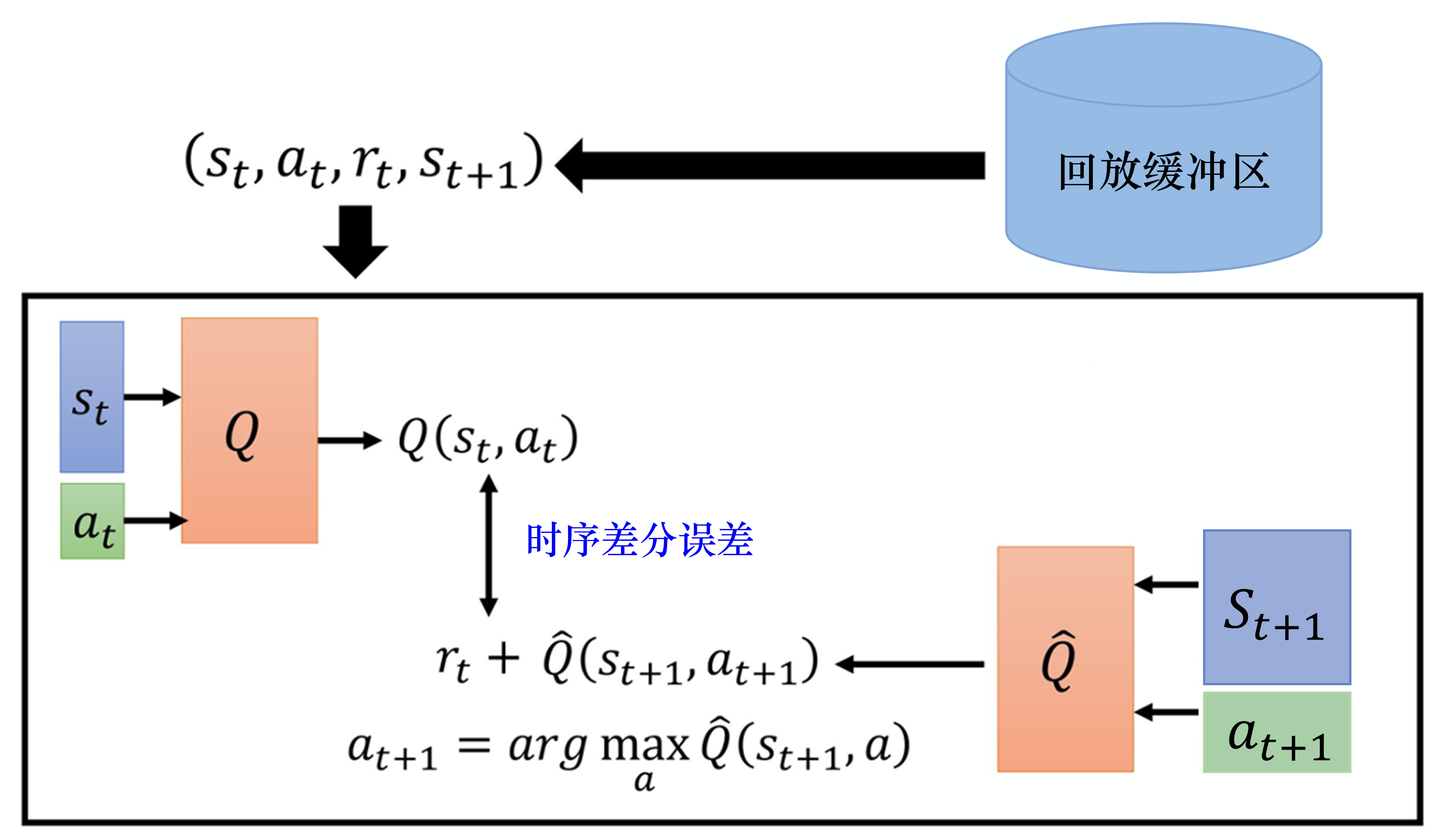
#经验回放
#Replay Buffer
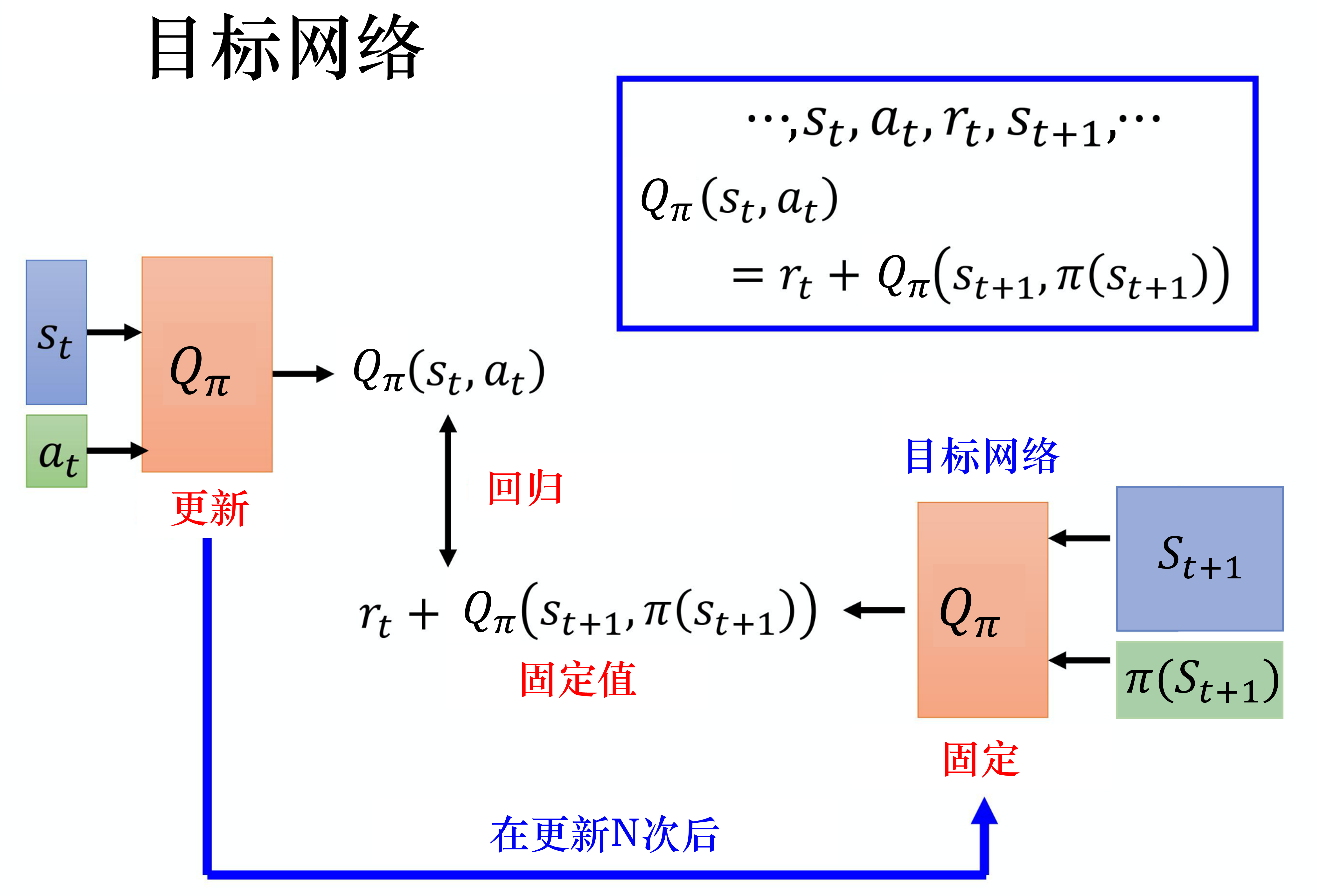
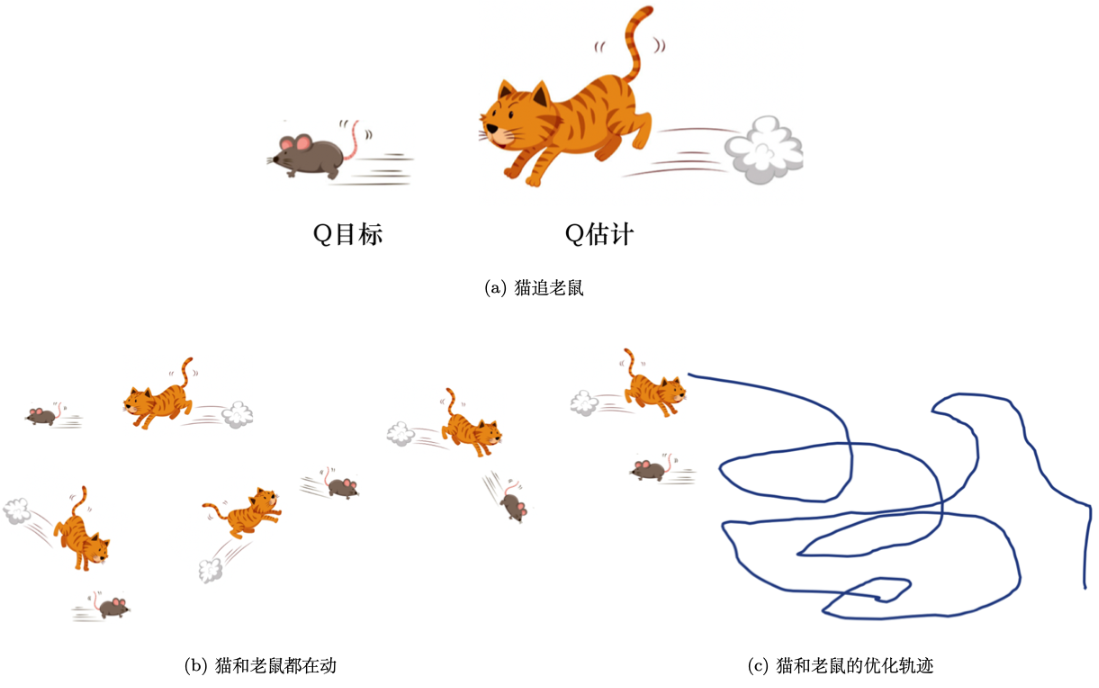
#目标网络
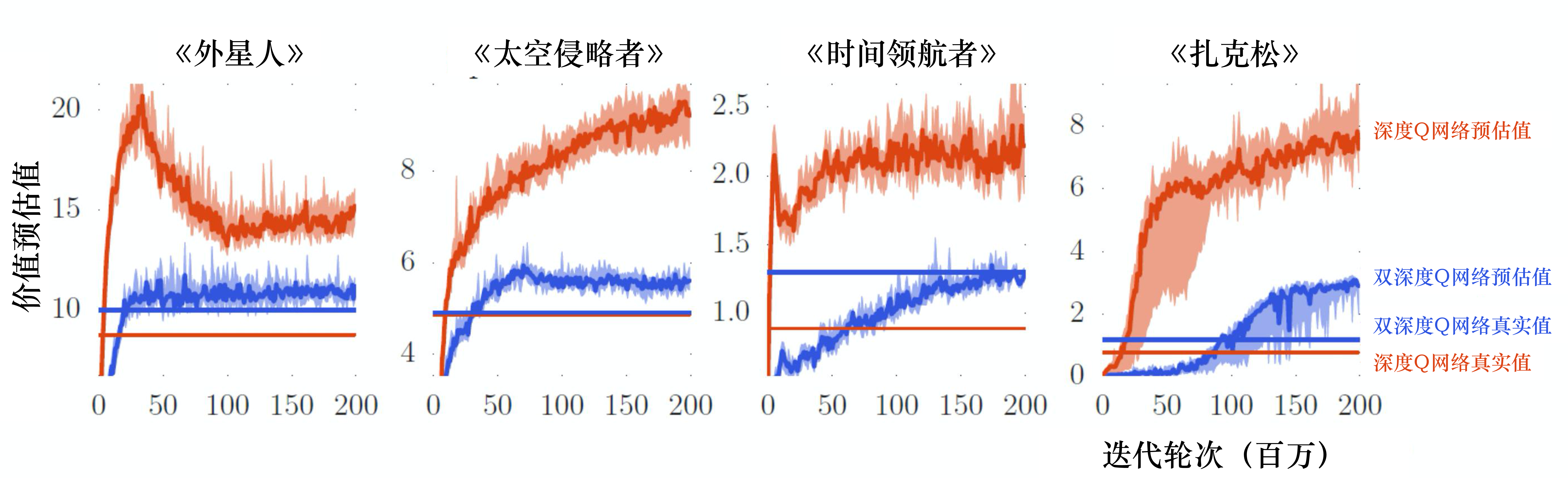
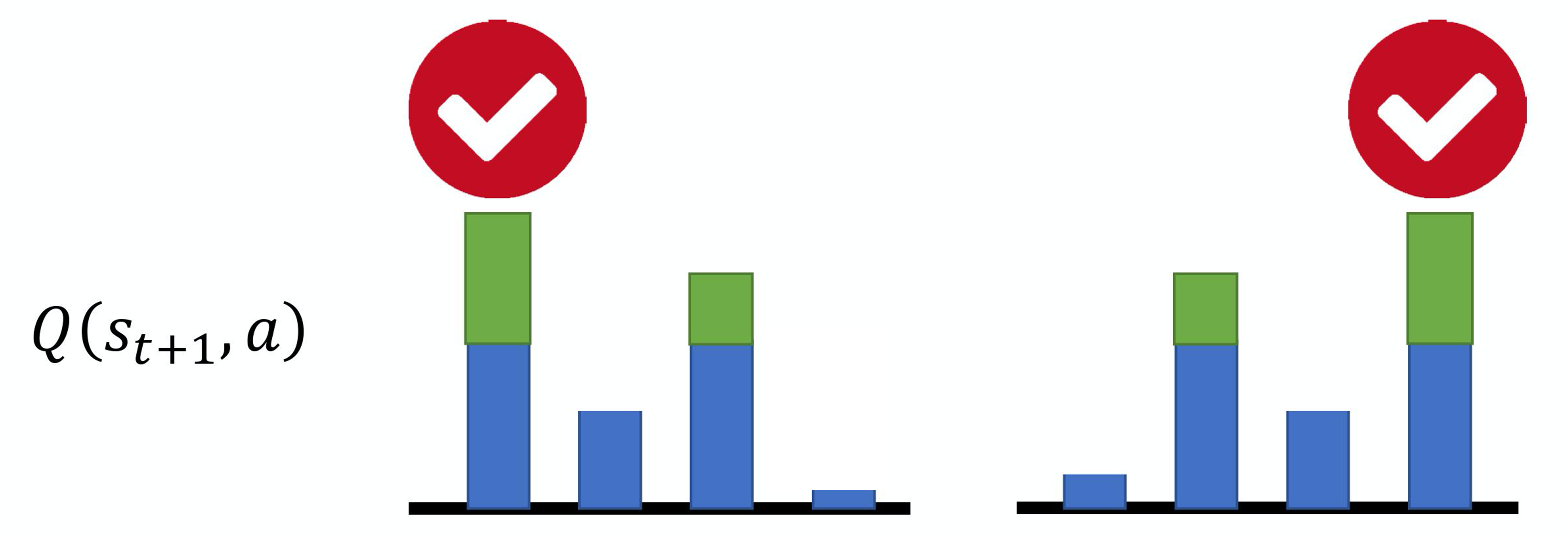
#Q值过估计
#Double DQN
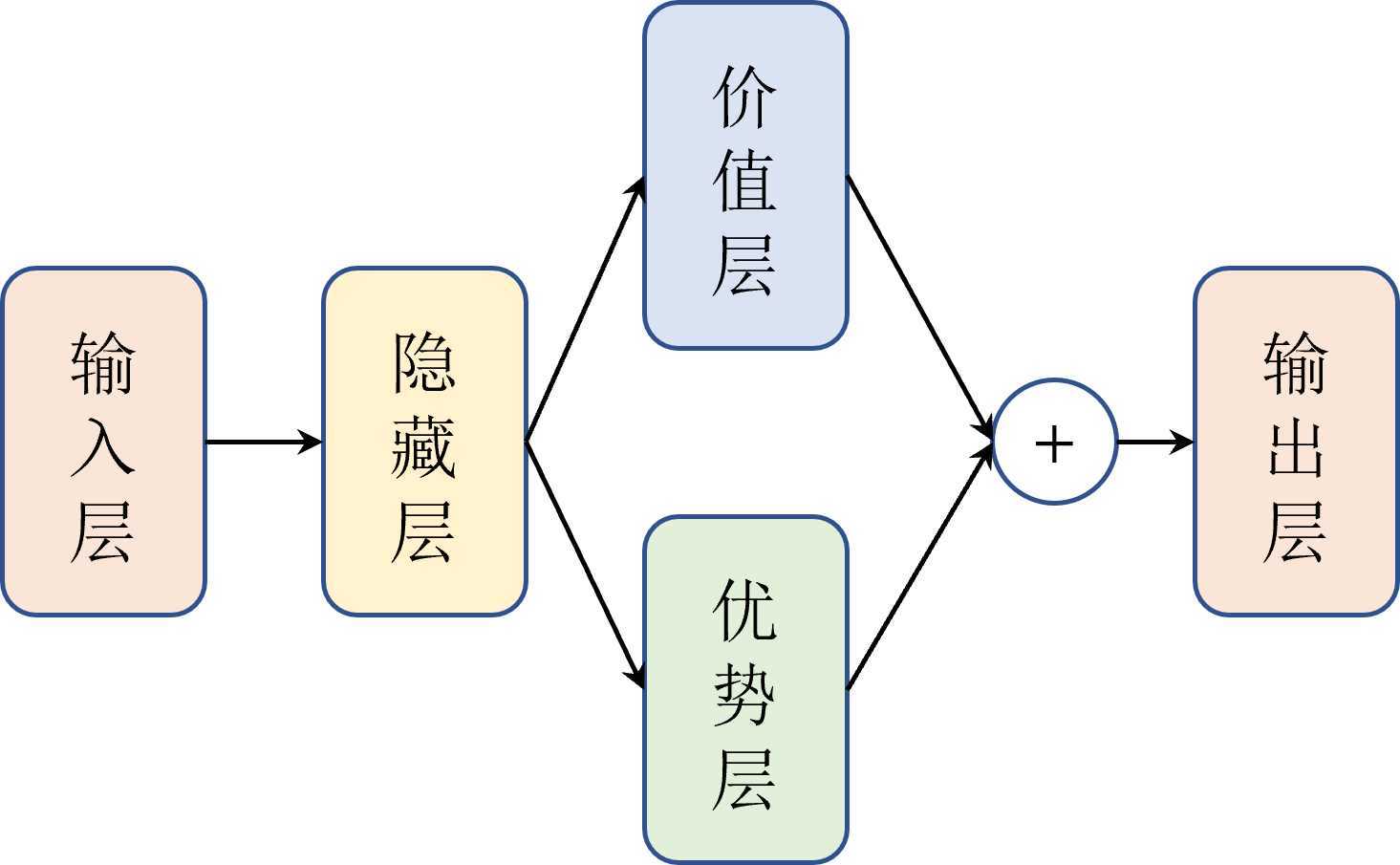
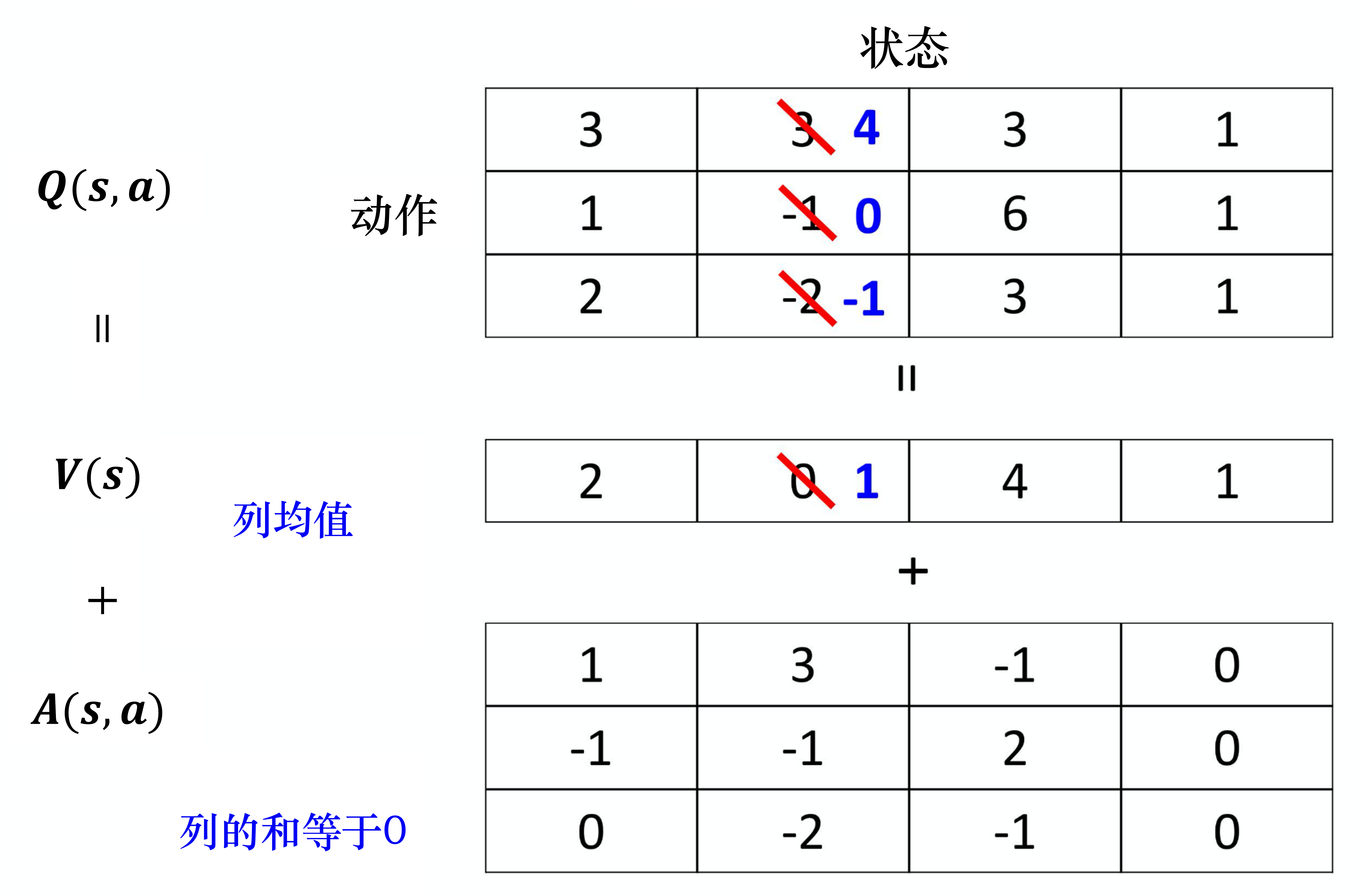
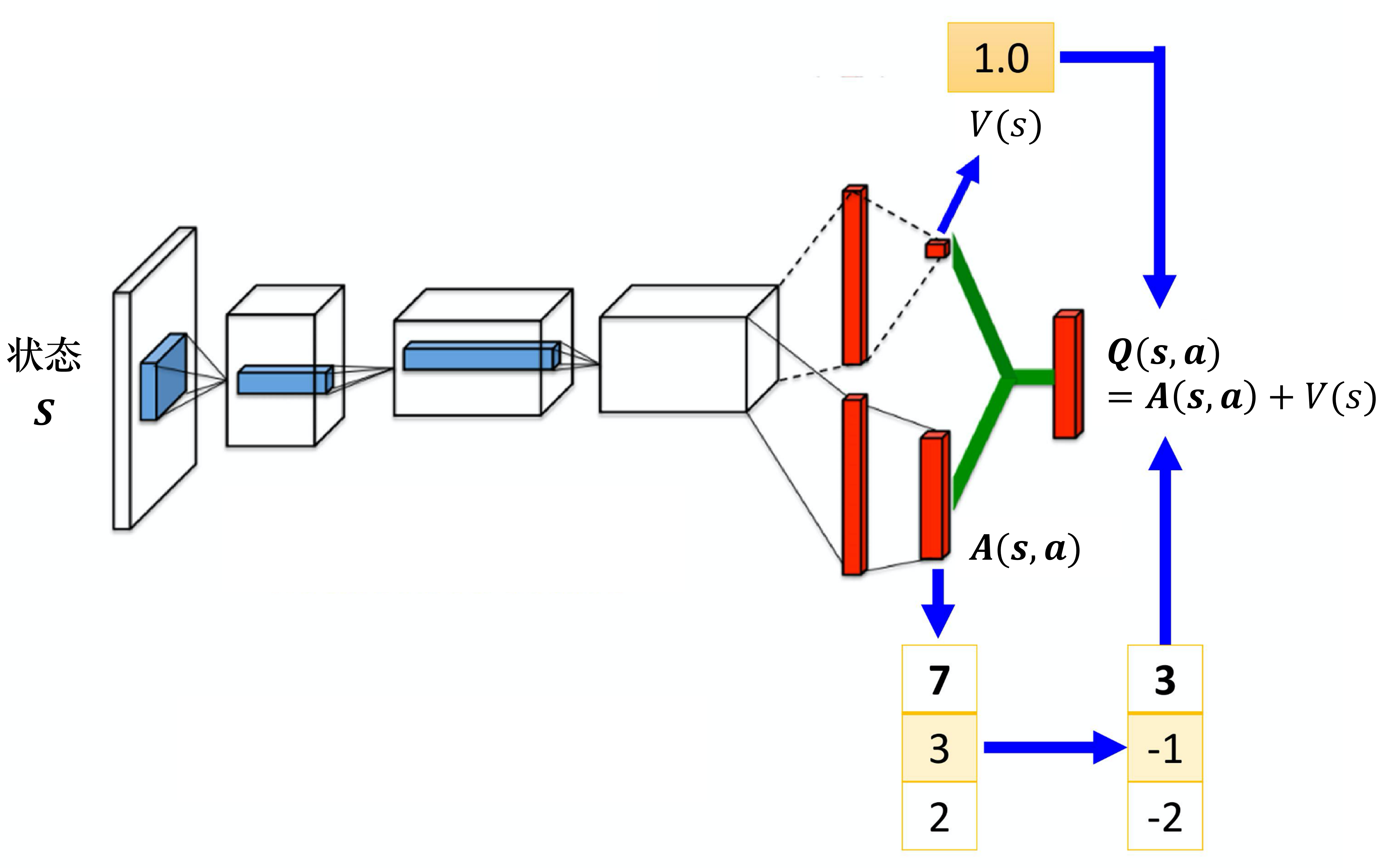
#Dueling DQN
#优势层
#价值层
#竞争更新
#优势约束
#Noisy DQN
#依赖状态的探索
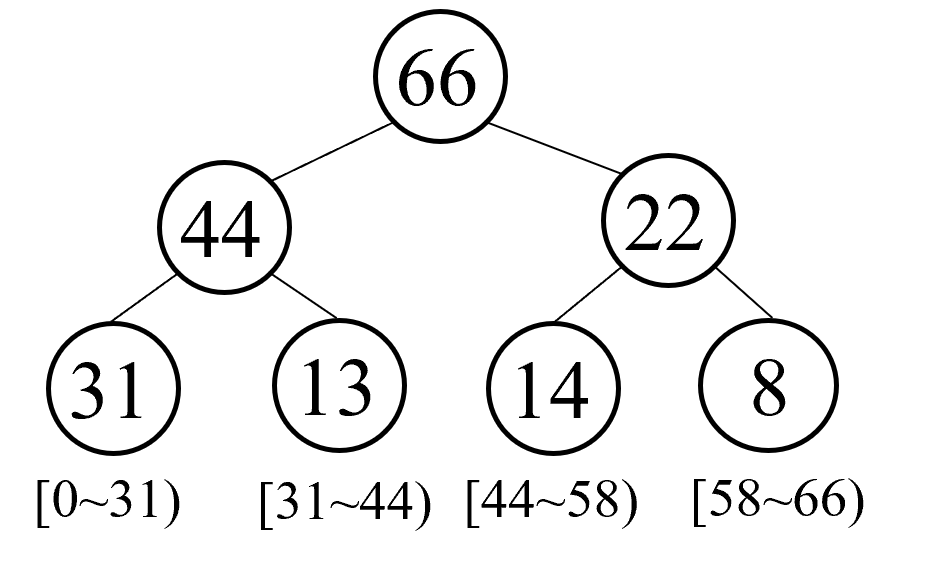
#优先级经验回放
#SumTree
#样本采样概率
#重要性采样权重
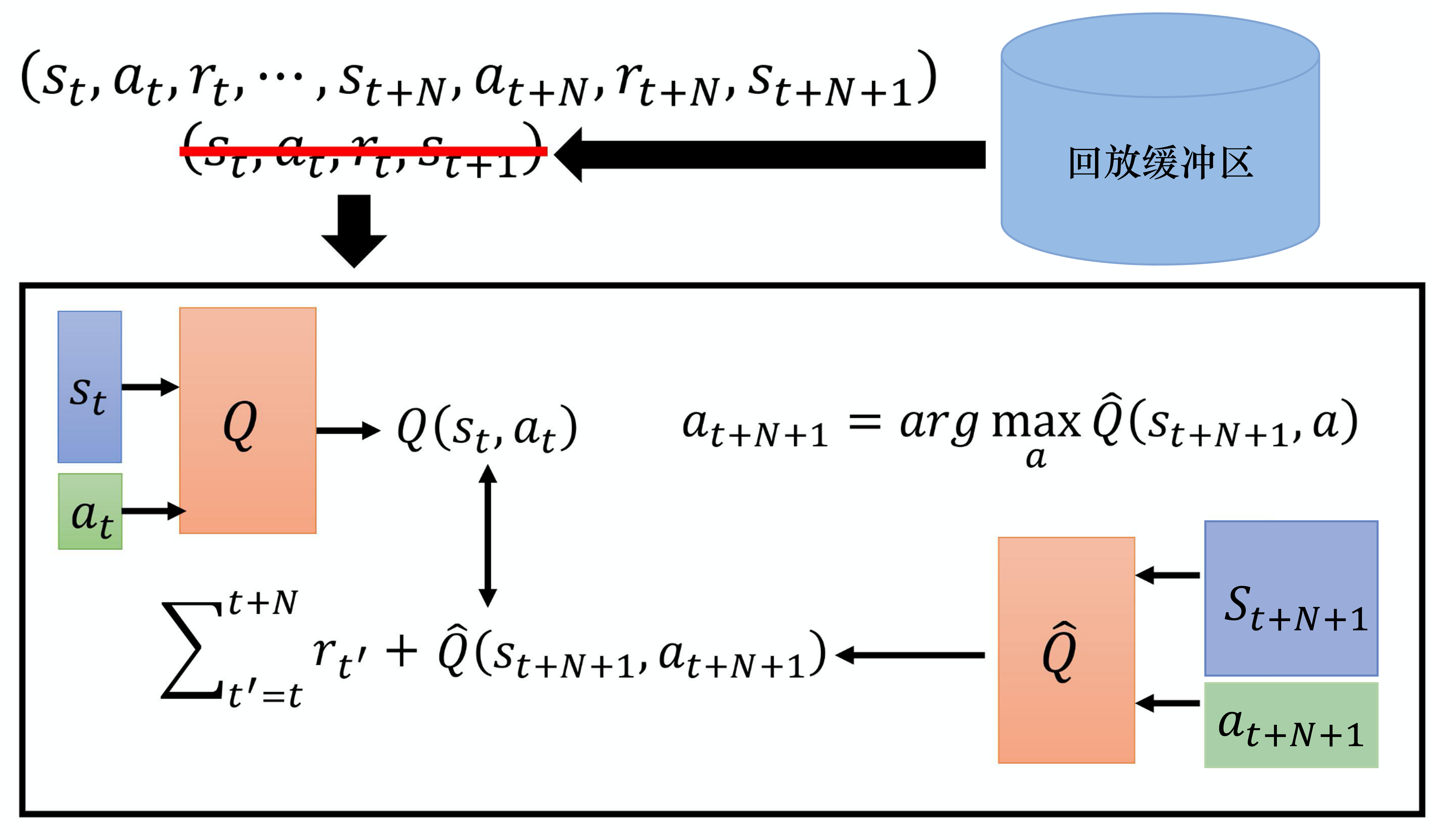
#MC-TD平衡
#多步方法
#分布Q网络
#彩虹