Word2vec有两种模型：CBOW和Skip-gram，有两种训练方法：Hierarchical Softmax和Negative Sampling。偏数学公式推导

背景介绍

符号

• $C$ ：语料Corpus，所有的文本内容，包含重复的词。
• D：词典，D是从C中取出来的，不重复。
• $w$：一个词语
• $m$：窗口大小，词语$w$的前后$m$个词语
• $\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}(\mathrm{w})={\mathrm{C}}_{\mathrm{w}}$： 词$w$的上下文词汇，取决于$m$
• $v(w)$： 词典$D$中单词$w$的词向量
• $k$：词向量的长度
• $i_w$：词语$w$在词典$D$中的下标
• $NEG(w)$ ： 词$w$的负样本子集

常用公式：

$$\begin{array}{rl}& \log (a^n{b}^m)=\log a^n+\log b^m=n\log a+m\log b\end{array}$$$$\log \prod _{i=1}{a}^i{b}^{1-i}=\sum _{i=1}\log a^i+\log b^{1-i}=\sum _{i=1}i\cdot \log a+(i-1)\cdot \log b$$

目标函数

n-gram模型。当然，我们使用神经概率语言模型。

$P(w\mid C_w)$ 表示上下文词汇推出中心单词$w$的概率。

对于统计语言模型来说，一般利用最大似然，把目标函数设为：

$$\prod _{w\in C}p(w\mid C_w)$$

一般使用最大对数似然，则目标函数为：

$$L=\sum _{w\in C}\log p(w\mid C_w)$$

其实概率$P(w\mid C_w)$是关于$w$和$C_w$的函数，其中$\theta$是待定参数集，就是要求最优 ${\theta }^{\ast }$，来确定函数$F$：

$$p(w\mid C_w)=F(w,C_w;\theta )$$

有了函数$F$以后，就能够直接算出所需要的概率。 而F的构造，就是通过神经网络去实现的。

神经概率语言模型

一个二元对$(C_w,w)$就是一个训练样本。神经网络结构如下，$W,U$是权值矩阵，$p,q$是对应的偏置。

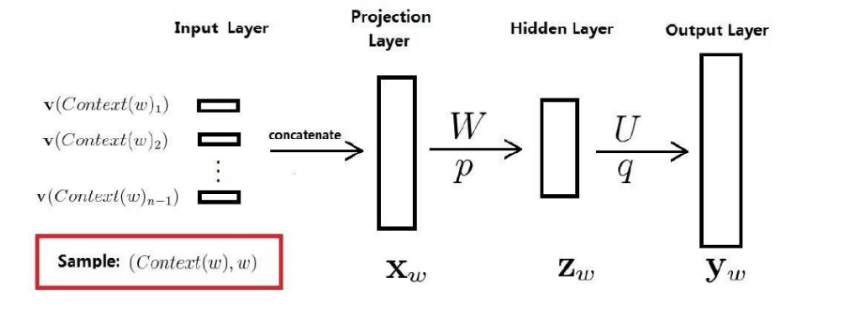
但是一般会减少一层，如下图：（其实是去掉了隐藏层，保留了投影层，是一样的）

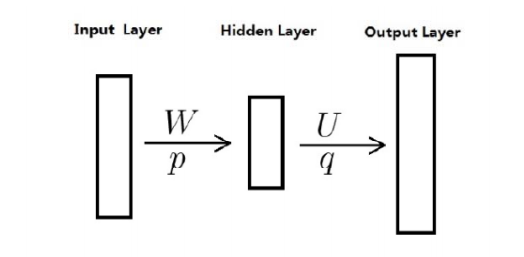
窗口大小是$m$，$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}(\mathrm{w})$包含$2m$个词汇，词向量长度是$k$。可以做拼接或者求和（下文是）。拼接得到长向量$2mk$， 在投影层得到${\mathbf{x}}_{\mathbf{w}}$，然后给到隐藏层和输出层进行计算。

$${\mathbf{z}}_w=\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(\mathrm{W}{\mathbf{z}}_{\mathrm{w}}+\mathbf{p})\to {\mathbf{y}}_{\mathrm{w}}=\mathrm{U}{\mathbf{z}}_{\mathrm{w}}+\mathbf{q}$$

再对${\mathbf{y}}_w=(y_1,y_2,\cdots ,y_K)$ 向量进行softmax即可得到所求得中心词汇的概率：

$$p(w\mid C_w)=\frac{e^{y_{i_w}}}{\sum _{i=1}^K{e}^{y_i}}$$

优点

• 词语的相似性可以通过词向量来体现
• 自带平滑功能。N-Gram需要自己进行平滑。

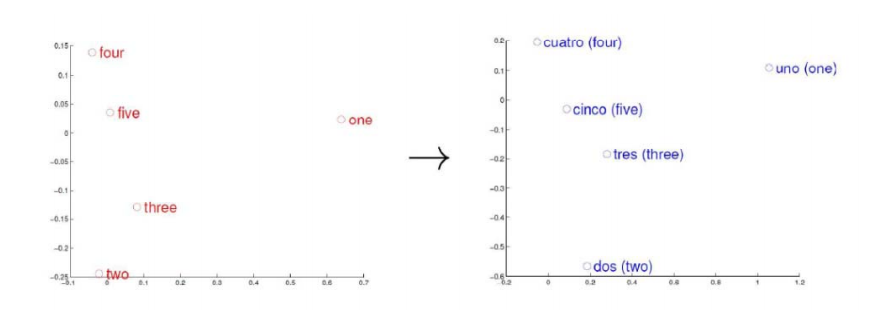
词向量的理解

有两种词向量，一种是one-hot representation，另一种是Distributed Representation。one-hot太长了，所以DR中把词映射成为相对短的向量。不再是只有1个1（孤注一掷），而是向量分布于每一维中（风险平摊）。再利用欧式距离就可以算出词向量之间的相似度。

传统可以通过LSA（Latent Semantic Analysis）和LDA（Latent Dirichlet Allocation）来获得词向量，现在也可以用神经网络算法来获得。

可以把一个词向量空间向另一个词向量空间进行映射，就可以实现翻译。

Hierarchical Softmax

两种模型都是基于下面三层模式（无隐藏层），输入层、投影层和输出层。没有hidden的原因是据说是因为计算太多了。

CBOW和Skip-gram模型：

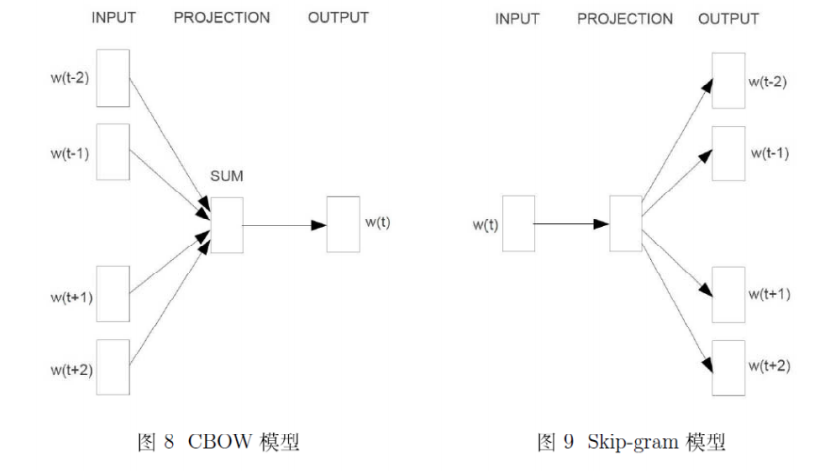
CBOW模型

一共有$\left|C\right|$个单词。CBOW是基于上下文$context(w)=c_w$去预测目标单词$w$，求条件概率$p(w\mid c_w)$，语言模型一般取目标函数为对数似然函数：

$$L=\sum _{w\in C}\log p(w\mid c_w)$$

窗口大小设为$m$，则$c_w$是$w$的前后m个单词。

输入层 是上下文单词的词向量。（初始随机，训练过程中逐渐更新）

投影层 就是对上下文词向量进行求和，向量加法。得到单词$w$的所有上下文词$c_w$的词向量的和${\mathbf{x}}_w$，待会儿参数更新的时候再依次更新回来。

输出层 从$C$中选择一个词语，实际上是多分类。这里是哈夫曼树层次softmax。

因为词语太多，用softmax太慢了。多分类实际上是多个二分类组成的，比如SVM二叉树分类：

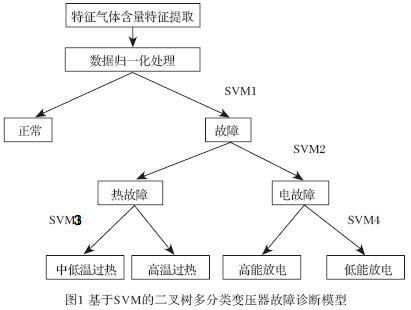
这是一种二叉树结构，应用到word2vec中，被称为Hierarchical Softmax。CBOW完整结构如下：

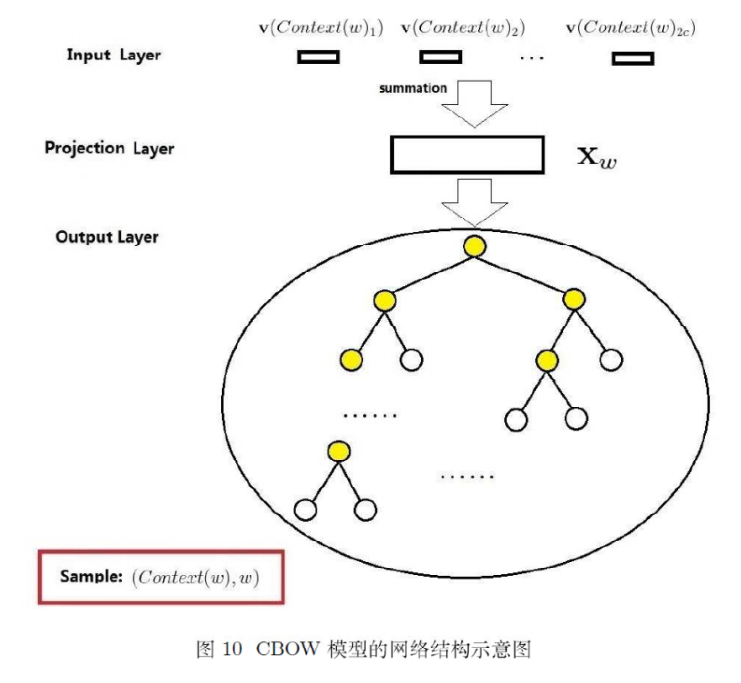
每个叶子节点代表一个词语$w$，每个词语被01唯一编码。

哈夫曼编码

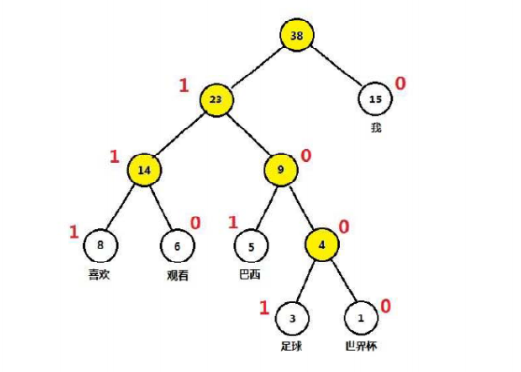
哈夫曼树很简单。每次从许多节点中，选择权值最小的两个合并，根节点为合并值；依次循环，直到只剩一棵树。

比如“我 喜欢 看 巴西 足球 世界杯”，这6个词语，出现的次数依次是15, 8, 6, 5, 3, 1。建立得到哈夫曼树，并且得到哈夫曼编码，如下：

CBOW足球例子

引入一些符号：

• $p^w$ ：从根节点到达$w$叶子节点的路径
• $l^w$ ： 路径$p^w$中节点的个数
• $p_1^w,\cdots ,p_{l_w}^w$ ：依次代表路径中的节点，根节点-中间节点-叶子节点
• $d_2^w,\cdots ,d_{l^w}^w\in \{0,1\}$：词$w$的哈夫曼编码，由$l^w-1$位构成， 根节点无需编码
• ${\theta }_1^w,\cdots ,{\theta }_{l^w-1}^w$：路径中非叶子节点对应的向量， 用于辅助计算。
• 单词$w$是足球，对应的所有上下文词汇是$c_w$， 上下文词向量的和是${\mathbf{x}}_w$

看一个例子：

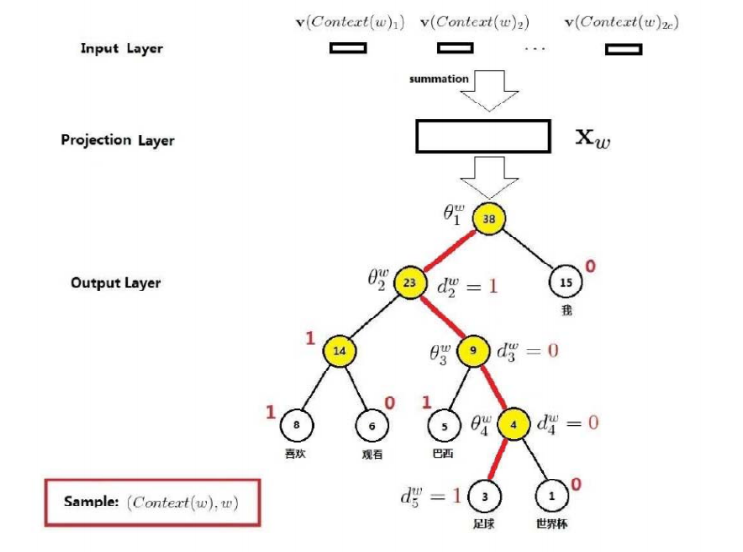
约定编码为1是负类，为0是正类。即左边是负类，右边是正类。

每一个节点就是一个二分类器，是逻辑回归(sigmoid)。其中$\theta$是对应的非叶子节点的向量，一个节点被分为正类和负类的概率分别如下：

$$\sigma ({\mathbf{x}}_w^T\theta )=\frac{1}{1+e^{-{\mathbf{x}}_w^T\theta }},1-\sigma ({\mathbf{x}}_w^T\theta )$$

那么从根节点到达足球的概率是：

$$p(\mathrm{足}\mathrm{球}\mid c_{\mathrm{足}\mathrm{球}})=\prod _{j=2}^{5}p(d_j^w\mid {\mathbf{x}}_w,{\theta }_{j-1}^w)$$

CBOW总结

目标函数

从根节点到每一个单词$w$都存在一条路径$p^w$，路径上有$l^w-1$个分支节点，每个节点就是一个二分类，每次产生一个概率 $p(d_j^w\mid {\mathbf{x}}_w,{\theta }_{j-1}^w)$， 把这些概率乘起来就得到了$p(w\mid c_w)$。

其中每个节点的概率是，与各个节点的参数和传入的上下文向量和${\mathbf{x}}_w$相关。

$$p(d_j^w\mid {\mathbf{x}}_w,{\theta }_{j-1}^w)=\{\begin{array}{lll}& \sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w),& d_j^w=0\\ & 1-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w),& d_j^w=1\end{array}$$

写成指数形式是

$$p(d_j^w\mid {\mathbf{x}}_w,{\theta }_{j-1}^w)=[\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w){]}^{1-d_j^w}\cdot [1-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w){]}^{d_j^w}$$

则上下文推中间单词的概率，即目标函数：

$$p(w\mid c_w)=\prod _{j=2}^{l^w}p(d_j^w\mid {\mathbf{x}}_w,{\theta }_{j-1}^w)$$

对数似然函数

对目标函数取对数似然函数是：

$$\begin{array}{rl}L& =\sum _{w\in C}\log p(w\mid c_w)=\sum _{w\in C}\log \prod _{j=2}^{l^w}[\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w){]}^{1-d_j^w}\cdot [1-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w){]}^{d_j^w}\\ & =\sum _{w\in C}\sum _{j=2}^{l^w}((1-d_j^w)\cdot \log \sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w)+d_j^w\cdot \log (1-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w)))\\ & =\sum _{w\in C}\sum _{j=2}^{l^w}((1-d_j^w)\cdot \log A+d_j^w\cdot \log (1-A)))\end{array}$$

简写：

$$\begin{array}{rl}& L(w,j)=(1-d_j^w)\cdot \log \sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w)+d_j^w\cdot \log (1-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w))\\ & L=\sum _{w,j}L(w,j)\end{array}$$

怎样最大化对数似然函数呢，可以最大化每一项，或者使整体最大化。尽管最大化每一项不一定使整体最大化，但是这里还是使用最大化每一项$L(w,j)$。

sigmoid函数的求导：

$${\sigma }^{\prime }(x)=\sigma (x)(1-\sigma (x))$$

$L(w,j)$有两个参数：输入层的${\mathbf{x}}_w$ 和 每个节点的参数向量${\theta }_{j-1}^w$ 。 分别求偏导并且进行更新参数：

$$\begin{array}{rl}& \frac{\partial }{{\theta }_{j-1}^w}L(w,j)=[1-d_j^w-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w)]\cdot {\mathbf{x}}_w\to {\theta }_{j-1}^w={\theta }_{j-1}^w+\alpha \cdot \frac{\partial }{{\theta }_{j-1}^w}L(w,j)\\ & \frac{\partial }{{\mathbf{x}}_w}L(w,j)=[1-d_j^w-\sigma ({\mathbf{x}}_w^T{\theta }_{j-1}^w)]\cdot {\theta }_{j-1}^w\to v(\hat{w})+=v(\hat{w})+\alpha \cdot \sum _{j=2}^{l^w}\frac{\partial }{{\mathbf{x}}_w}L(w,j),\hat{w}\in c_w\end{array}$$

注意：${\mathbf{x}}_w$是所有上下文词向量的和，应该把它的更新平均更新到每个上下文词汇中去。$\hat{w}$ 代表$c_w$中的一个词汇。

Skip-Gram模型

Skip-gram模型是根据当前词语，预测上下文。网络结构依然是输入层、投影层(其实无用)、输出层。如下：

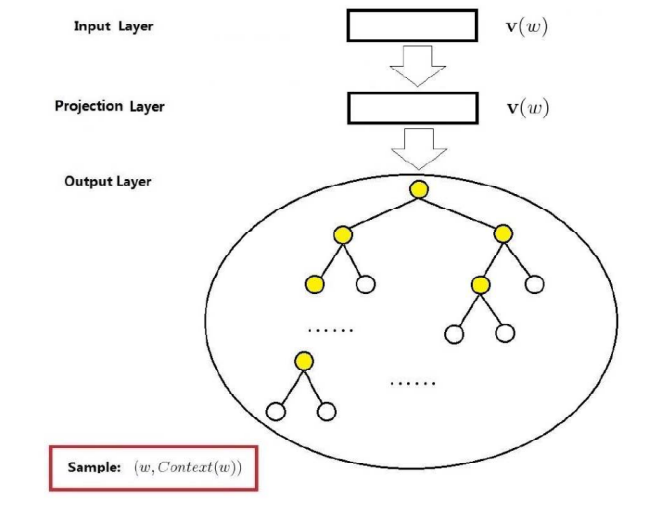
输入一个中心单词的词向量$v(w)$，简记为$v_w$，输出是一个哈夫曼树。单词$u$是$w$的上下文单词$c_w$中的一个。这是一个词袋模型，每个$u$是互相独立的。

目标函数

所以$c_w$是$w$的上下文词汇的概率是：

$$p(c_w\mid w)=\prod _{u\in c_w}p(u\mid w)$$

与上面同理，$p(u\mid w)$ 与传入的中心单词向量$v(w)$和路径上的各个节点相关：

$$\begin{array}{rl}& p(u\mid w)=\prod _{j=2}^{l^w}p(d_j^u\mid v_w,{\theta }_{j-1}^u)\\ & p(d_j^u\mid v_w,{\theta }_{j-1}^u)=[\sigma (v_w^T{\theta }_{j-1}^u){]}^{1-d_j^u}\cdot [1-\sigma (v_w^T{\theta }_{j-1}^u){]}^{d_j^u}\end{array}$$

下文$v_w^T{\theta }_{j-1}^w$简记为$v_w{\theta }_{j-1}^w$，要记得转置向量相乘就可以了。

对数似然函数

$$\begin{array}{rl}L& =\sum _{w\in C}\log p(c_w\mid w)\\ & =\sum _{w\in C}\log \prod _{u\in c_w}\prod _{j=2}^{l^w}[\sigma (v_w^T{\theta }_{j-1}^u){]}^{1-d_j^u}\cdot [1-\sigma (v_w^T{\theta }_{j-1}^u){]}^{d_j^u}\\ & =\sum _{w\in C}\sum _{u\in c_w}\sum _{j=2}^{l^w}((1-d_j^u)\cdot \log \sigma (v_w^T{\theta }_{j-1}^u)+d_j^u\cdot \log (1-\sigma (v_w^T{\theta }_{j-1}^u)))\end{array}$$

同样，简写每一项为$L(w,u,j)$

$$L(w,u,j)=(1-d_j^u)\cdot \log \sigma (v_w^T{\theta }_{j-1}^u)+d_j^u\cdot \log (1-\sigma (v_w^T{\theta }_{j-1}^u))$$

然后就是，分别对$v_w$和${\theta }_{j-1}^u$求梯度更新即可，同上面的类似。得到下面的更新公式

$$\begin{array}{rl}& {\theta }_{j-1}^u={\theta }_{j-1}^u+\alpha \cdot [1-d_j^u-\sigma (v_w^t\cdot {\theta }_{j-1}^u)]\cdot v(w)\\ & v_w=v_w+\alpha \cdot \sum _{u\in c_w}\sum _{j=2}^{l^w}\frac{\partial L(w,u,j)}{\partial v_w}\end{array}$$

Negative Sampling

背景知识介绍

Negative Sampling简称NEG，是Noise Contrastive Estimation(NCE)的一个简化版本，目的是用来提高训练速度和改善所得词向量的质量。

NEG不使用复杂的哈夫曼树，而是使用随机负采样，大幅度提高性能，是Hierarchical Softmax的一个替代。

NCE 细节有点复杂，本质上是利用已知的概率密度函数来估计未知的概率密度函数。简单来说，如果已知概率密度X，未知Y，如果知道X和Y的关系，Y也就求出来了。

在训练的时候，需要给正例和负例。Hierarchical Softmax是把负例放在二叉树的根节点上，而NEG，是随机挑选一些负例。

CBOW

对于一个单词$w$，输入上下文$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}(\mathrm{w})={\mathrm{C}}_{\mathrm{w}}$，输出单词$w$。那么词$w$是正样本**，**其他词都是负样本。 负样本很多，该怎么选择呢？后面再说。

定义$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}(\mathrm{w})$的负样本子集$\mathrm{N}\mathrm{E}\mathrm{G}(\mathrm{w})$。对于样本$(C_w,w)$，${\mathbf{x}}_w$依然是$C_w$的词向量之和。${\theta }_u$为词$u$的一个（辅助）向量，待训练参数。

设集合$S_w=w\bigcup NEG(w)$ ，对所有的单词$u\in S_w$，有标签函数：

$$b^w(u)=\{\begin{array}{lll}& 1,& u=w\\ & 0,& u\ne w\end{array}$$

单词$u$是$C_w$ 的中心词的概率是：

$$p(u\mid C_w)=\{\begin{array}{lll}& \sigma ({\mathbf{x}}_w^T{\theta }^u),& u=w\text{正样本}\\ & 1-\sigma ({\mathbf{x}}_w^T{\theta }^u),& u\ne w\text{负样本}\end{array}$$

简写为：

$$p(u\mid C_w)=[\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{b^w(u)}\cdot [1-\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{1-b^w(u)}$$

要最大化目标函数$g(w)=\sum _{u\in S_w}p(u\mid C_w)$：

$$\begin{array}{rl}g(w)& =\prod _{u\in S_w}[\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{b^w(u)}\cdot [1-\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{1-b^w(u)}\\ & =\sigma ({\mathbf{x}}_w^T{\theta }^u)\prod _{u\in NEG(w)}(1-\sigma ({\mathbf{x}}_w^T{\theta }^u))\end{array}$$

观察$g(w)$可知，最大化就是要：增大正样本概率和减小化负样本概率。

每个词都是这样，对于整个语料库的所有词汇，将$g$累计得到优化目标，目标函数如下：

$$\begin{array}{rl}L& =\log \prod _{w\in C}g(w)=\sum _{w\in C}\log g(w)\\ & =\sum _{w\in C}\log (\prod _{u\in S_w}[\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{b^w(u)}\cdot [1-\sigma ({\mathbf{x}}_w^T{\theta }^u){]}^{1-b^w(u)})\\ & =\sum _{w\in C}\sum _{u\in S_w}[b_u^w\cdot \sigma ({\mathbf{x}}_w^T{\theta }^u)+(1-b_u^w)\cdot (1-\sigma ({\mathbf{x}}_w^T{\theta }^u))]\end{array}$$

简写每一步$L(w,u)$：

$$L(w,u)=b_u^w\cdot \sigma ({\mathbf{x}}_w^T{\theta }^u)+(1-b_u^w)\cdot (1-\sigma ({\mathbf{x}}_w^T{\theta }^u))$$

计算$L(w,u)$对${\theta }^u$和${\mathbf{x}}_w$的梯度进行更新，得到梯度(对称性)：

$$\frac{\partial L(w,u)}{\partial {\theta }^u}=[b^w(u)-\sigma ({\mathbf{x}}_w^T{\theta }^u)]\cdot {\mathbf{x}}_w,\frac{\partial L(w,u)}{\partial {\mathbf{x}}_w}=[b^w(u)-\sigma ({\mathbf{x}}_w^T{\theta }^u)]\cdot {\theta }^u$$

更新每个单词的训练参数${\theta }^u$ ：

$${\theta }^u={\theta }^u+\alpha \cdot \frac{\partial L(w,u)}{\partial {\theta }^u}$$

对每个单词更新词向量$v(u)$ ：

$$v(u)=v(u)+\alpha \cdot \sum _{u\in S_w}\frac{\partial L(w,u)}{\partial {\mathbf{x}}_w}$$

Skip-gram

H给单词$w$，预测上下文向量$\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{x}\mathrm{t}(\mathrm{w})={\mathrm{C}}_{\mathrm{w}}$。 输入样本$(w,C_w)$。

中心单词是$w$，遍历样本中的上下文单词$w_o\in C_w$，为每个上下文单词$w_o$生成一个包含负采样的集合$S_o=w\bigcup \mathrm{N}\mathrm{E}\mathrm{G}(\mathrm{o})$ 。即$S_o$里面只有$w$才是$o$的中心单词。

下面$w_o$简写为$o$，要注意实际上是当前中心单词$w$的上下文单词。

$S_o$中的$u$是实际的w就为1，否则为0。标签函数如下：

$$b^w(u)=\{\begin{array}{lll}& 1,& u=w\\ & 0,& u\ne w\end{array}$$

$S_o$中的$u$是$o$的中心词的概率是

$$p(u\mid o)=\{\begin{array}{lll}& \sigma (v_o^T{\theta }^u),& u=w\leftrightarrow b^w(u)=1\\ & 1-\sigma (v_o^T{\theta }^u),& u\ne w\leftrightarrow b^w(u)=0\end{array}$$

简写为

$$p(u\mid o)=[\sigma (v_o^T{\theta }^u){]}^{b^w(u)}\cdot [1-\sigma (v_o^T{\theta }^u){]}^{1-b^w(u)}$$

对于$w$的一个上下文单词$o$来说，要最大化这个概率：

$$\prod _{u\in S_o}p(u\mid o)$$

对于$w$的所有上下文单词$C_w$来说，要最大化：

$$g(w)=\prod _{o\in C_w}\prod _{u\in S_o}p(u\mid o)$$

那么，对于整个预料，要最大化：

$$G=\prod _{w\in C}g(w)=\prod _{w\in C}\prod _{o\in C_w}\prod _{u\in S_o}p(u\mid o)$$

对G取对数，最终的目标函数就是：

$$\begin{array}{rl}L& =\log G=\sum _{w\in C}\sum _{o\in C_w}\log \prod _{u\in S_o}p(u\mid o)\\ & =\sum _{w\in C}\sum _{o\in C_w}\log \prod _{u\in S_o}[\sigma (v_o^T{\theta }^u){]}^{b^w(u)}\cdot [1-\sigma (v_o^T{\theta }^u){]}^{1-b^w(u)}\\ & =\sum _{w\in C}\sum _{o\in C_w}\sum _{u\in S_o}(b_u^w\cdot \sigma (v_o^T{\theta }^u)+(1-b_u^w)\cdot (1-\sigma (v_o^T{\theta }^u)))\end{array}$$

取$w,o,u$简写L(w, o, u)：

$$L(w,o,u)=b_u^w\cdot \sigma (v_o^T{\theta }^u)+(1-b_u^w)\cdot (1-\sigma (v_o^T{\theta }^u))$$

分别对${\theta }^u、v_o$求梯度

$$\frac{\partial L(w,o,u)}{\partial {\theta }^u}=[b_u^w-\sigma (v_o^T{\theta }^u)]\cdot v_o,\frac{\partial L(w,o,u)}{\partial v_o}=[b_u^w-\sigma (v_o^T{\theta }^u)]\cdot {\theta }^u$$

更新每个单词的训练参数${\theta }^u$ ：

$${\theta }^u={\theta }^u+\alpha \cdot \frac{\partial L(w,o,u)}{\partial {\theta }^u}$$

对每个单词更新词向量$v(o)$ ：

$$v(o)=v(o)+\alpha \cdot \sum _{u\in S_o}\frac{\partial L(w,u)}{\partial v_o}$$