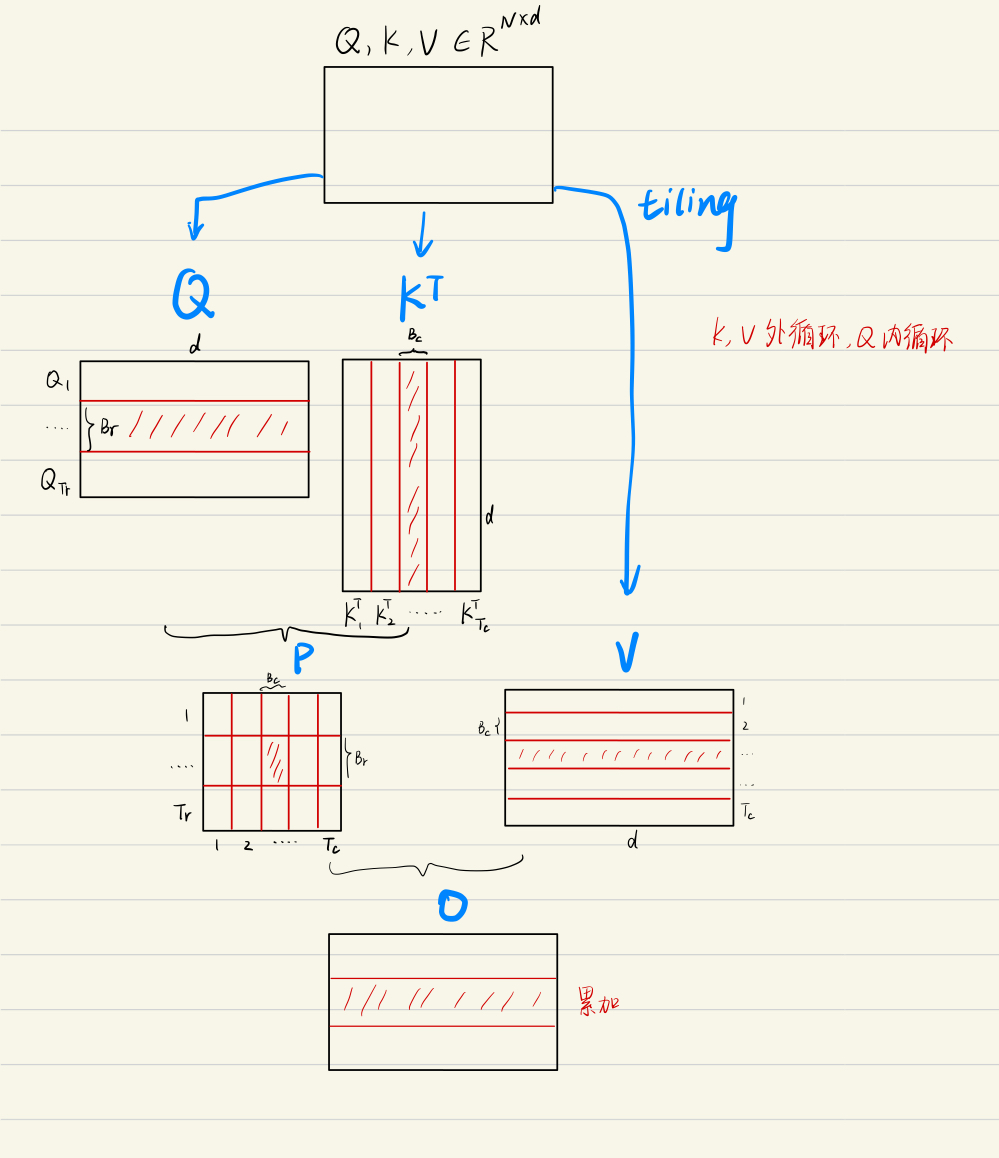
概览

分类	方法	核心思想	主要解决的问题
基础	Traditional Softmax Attention	计算完整的 N x N 注意力矩阵	建立序列依赖关系
算法优化	Linear Attention	利用矩阵乘法结合律，近似计算	O(N²) 复杂度
	Sparse Attention	只计算部分重要的注意力权重	O(N²) 复杂度
架构创新	Multi-Head Attention	并行计算多个子空间的注意力	提升模型表达能力
	Multi-Query / Group-Query Attention	多组/所有头 共享K和V	MHA的KVCache显存瓶颈
	Multi-Head Latent Attention	引入信息瓶颈（潜向量）	处理超长序列的 O(N²) 复杂度
实现优化	Flash Attention	分块计算，避免读写巨大中间矩阵	内存带宽瓶颈，硬件利用率低

标准Softmax Attention/Full Attention

参考文章

大牛博客

• 线性注意力简史：从模仿、创新到反哺

早期笔记

• 各种注意力总结。
• 图文介绍RNN注意力机制。
• 机器翻译注意力机制及其PyTorch实现
• 大名鼎鼎的Transformer

标准Softmax注意力公式

标准 Softmax Attention

符号定义

$${\mathit{q}}_i,{\mathit{k}}_i,{\mathit{v}}_i,{\mathit{o}}_i\in {\mathbb{R}}^{d\times 1}$$$$\begin{array}{ll}& \mathit{Q}=[{\mathit{q}}_1,{\mathit{q}}_2,\cdots ,{\mathit{q}}_n{]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times d}\\ & \mathit{K}=[{\mathit{k}}_1,{\mathit{k}}_2,\cdots ,{\mathit{k}}_n{]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times d}\\ & \mathit{V}=[{\mathit{v}}_1,{\mathit{v}}_2,\cdots ,{\mathit{v}}_n{]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times d}\\ & \mathit{O}=[{\mathit{o}}_1,{\mathit{o}}_2,\cdots ,{\mathit{o}}_n{]}^{\mathrm{\top }}\in {\mathbb{R}}^{n\times d}\end{array}$$

• Q、K的维度和V、O的维度可以不相同，参考MLA。

核心思想

• 注意力本质：$\mathit{Q}\mathbf{,}\mathit{K}\mathbf{,}\mathit{V}\to \mathit{O}$ 映射。

• Causal场景：${\mathit{o}}_t$ 至多和 ${\mathit{Q}}_{[:t]},{\mathit{K}}_{[:t]},{\mathit{V}}_{[:t]}$ 有关。

  $$\mathit{O}=\text{softmax}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}+\log \mathit{M})\cdot \mathit{V}$$

• $\mathit{M}\in {\mathbb{R}}^{n\times n}$：掩码矩阵，下三角矩阵

  $${\mathit{M}}_{i,j}=\{\begin{array}{ll}1,& i\ge j\\ 0,& i<j\end{array}$$
  • $\log \mathit{M}$，对M的分量逐一取log，$\log \mathbf{0}=-\mathrm{\infty }$

Softmax Attention 分量形式

• 分母：权重和，分子每项的权重*值，再求和。除以分母：保持数值稳定性

$${\mathit{o}}_t=\frac{\sum _{j=1}^t\exp ({\mathit{q}}_t^{\mathrm{\top }}{\mathit{k}}_j){\mathit{v}}_j}{\sum _{j=1}^t\exp ({\mathit{q}}_t^{\mathrm{\top }}{\mathit{k}}_j)}$$

• 简单示例，多项V加权求和

$$o_5=\frac{q_5{k}_1}{\text{sum}}\cdot v_1+\frac{q_5{k}_2}{\text{sum}}\cdot v_2+\frac{q_5{k}_3}{\text{sum}}\cdot v_3+\frac{q_5{k}_4}{\text{sum}}\cdot v_4+\frac{q_5{k}_5}{\text{sum}}\cdot v_5$$

Softmax Attention 精简

• 最核心为分子，需把 $n\times n$的矩阵$\text{exp}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})$算出来，空间和时间复杂度，都正比于$n^2$

  $$\mathit{O}=\text{exp}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}+\log \mathit{M})\cdot \mathit{V}=(\text{exp}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})\odot \mathit{M})\mathit{V}$$

• 精简：去掉softmax

  $$\mathit{O}=(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}\odot \mathit{M})\mathit{V}$$

• 精简：去掉掩码，非causal

  $$\mathit{O}=(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})\mathit{V}=\mathit{Q}({\mathit{K}}^{\mathrm{\top }}\mathit{V})$$

• 增加归一化

  $$\mathit{O}=\text{RMSNorm}((\mathit{Q}{\mathit{K}}^{\mathrm{\top }}\odot \mathit{M})\mathit{V})$$

注意力精简公式

注意力精简公式

Attention 精简公式

$${\mathit{o}}_t=\text{Attn}({\mathit{q}}_t,{\mathit{k}}_{:t},{\mathit{v}}_{:t})$$$${\mathit{o}}_t=\text{Attn}({\mathit{q}}_t,{\mathit{k}}_{:t},{\mathit{v}}_{:t})=\sum _{i=1}^t\frac{{\alpha }_{t,i}\cdot {\mathit{v}}_i}{\sum _{j=1}^t{\alpha }_{t,j}}$$$${\alpha }_{t,i}=e^{\frac{{\mathit{q}}_t^{\mathrm{\top }}{\mathit{k}}_i}{\sqrt{d_k}}}=e^{{\mathit{q}}_t^{\mathrm{\top }}{\mathit{k}}_i}-e^{\sqrt{d_k}}$$

矩阵带掩码 公式

$$\mathit{O}=\text{softmax}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}+\log \mathit{M})\cdot \mathit{V}$$$$\mathit{O}=\text{exp}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}+\log \mathit{M})\cdot \mathit{V}=(\text{exp}(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})\odot \mathit{M})\mathit{V}$$

矩阵精简公式

$$\mathit{O}=(\mathit{Q}{\mathit{K}}^{\mathrm{\top }}\odot \mathit{M})\mathit{V}$$$$\mathit{O}=(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})\mathit{V}=\mathit{Q}({\mathit{K}}^{\mathrm{\top }}\mathit{V})$$$$\mathit{O}=\text{RMSNorm}((\mathit{Q}{\mathit{K}}^{\mathrm{\top }}\odot \mathit{M})\mathit{V})$$

Softmax和Linear时间复杂度

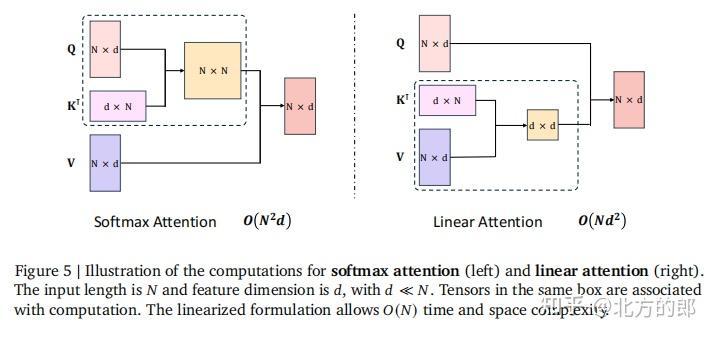
Softmax和线性注意力时间复杂度

Softmax和线性注意力

$$\mathit{O}=\underset{{\mathbb{R}}^{n\times n}}{\underbrace{(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})}}\underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{V}}}⟺\underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{Q}}}\underset{{\mathbb{R}}^{d\times d}}{\underbrace{({\mathit{K}}^{\mathrm{\top }}\mathit{V})}}$$

• 左侧：传统softmax注意力
  • 时间复杂度：$O(n\times n\times d)=O(d{n}^2)$
    • 第一步：$O(n\times d\times n)$；第二步：$O(n\times n\times d)$
    • 综合两步：$O(d{n}^2)+O(d{n}^2)=O(d{n}^2)$
  • 当n很大时：由于 $n^2$，计算成本非常高
  • Flash Attention降低了空间需求，但平方时间复杂度依然无法避免。
• 右侧：线性注意力。
  • 时间复杂度：$O(d\times n\times d)=O(n{d}^2)$
    • 第一步：$O(d\times n\times d)$；第二步：$O(d\times n\times d)$
    • 综合两步：$O(n{d}^2)+O(n{d}^2)=O(n{d}^2)$
  • 当n很大时，$d^2$为常数，复杂度随n线性递增，计算成本低
• 区别
  • 计算上：仅仅是交换了计算顺序

Softmax 时间复杂度例子

• $\mathit{Q}{\mathit{K}}^{\mathrm{\top }}$矩阵乘法 (传统softmax注意力)

  $$\underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{Q}}}\times \underset{{\mathbb{R}}^{d\times n}}{\underbrace{{\mathit{K}}^{\mathrm{\top }}}}=\mathit{W}\in {\mathbb{R}}^{n\times n}$$

  • 结果矩阵$\mathit{W}$共 $n\times n$个元素，第i行j列元素$W_{i,j}$计算过程

    • ${\mathit{Q}}_i$：第i列，d个元素的行向量，维度为 $1\times d$
    • ${\mathit{K}}_j^{\mathrm{\top }}$：第j行，d个元素的列向量，维度为 $d\times 1$
    $$W_{i,j}={\mathit{Q}}_i\cdot {\mathit{K}}_j^{\mathrm{\top }}=\sum _{l=1}^d{\mathit{Q}}_{i,l}\cdot {\mathit{K}}_{l,j}^{\mathrm{\top }}$$

  • 单个元素计算复杂度：$o(d)$，$d$次乘法、$d-1$次加法

  • 整体复杂度：有$n^2$个元素，共$\text{o}(d{n}^2)$

线性注意力时间复杂度例子

• ${\mathit{K}}^{\mathrm{\top }}\mathit{V}$矩阵乘法 (线性注意力)

  $$\underset{{\mathbb{R}}^{d\times n}}{\underbrace{{\mathit{K}}^{\mathrm{\top }}}}\times \underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{V}}}=\mathit{W}\in {\mathbb{R}}^{d\times d}$$

  • 结果矩阵$\mathit{W}$共 $d\times d$个元素，第i行j列元素$W_{i,j}$计算过程

    • ${\mathit{K}}_i^{\mathrm{\top }}$：第i行，n个元素的行向量，维度为 $1\times n$
    • ${\mathit{V}}_j$：第j列，n个元素的列向量，维度为 $n\times 1$
    $$W_{i,j}={\mathit{K}}_i^{\mathrm{\top }}\cdot {\mathit{V}}_j=\sum _{l=1}^n{\mathit{K}}_{i,l}^{\mathrm{\top }}\cdot {\mathit{V}}_{l,i}$$

  • 单个元素计算复杂度：$o(n)$，$n$次乘法、$n-1$次加法

  • 整体复杂度：有$d^2$个元素，共$\text{o}(n{d}^2)$，复杂度线性依赖于n

Attention 概念

Attention 概念

• Input：一般是一个句子；乘以矩阵得Q/K/V 3个向量

• QKV向量

  • Query：表示当前查询query
  • Key： Key是各个位置的键，
  • Value：Value各个位置的信息

• 注意力权重

  • $\text{softmax}(Q\ast K)$： 即当前query对各个位置的注意力权重${\alpha }_1,\cdots ,{\alpha }_l$。
  • 早期QK有 dot/concat/w 这3种score计算的3种方式

• 加权求和

  • 利用注意力权重对各位置Value加权求和，就得到输出

$$\text{Attention}(Q,K,V)=\text{softmax}(\frac{Q{K}^{\mathrm{\top }}}{\sqrt{d_k}})\cdot V$$

• 除以$\sqrt{d_k}$进行缩放，防止梯度爆炸,

Self-Attention vs 其他Attention

Self-Attention

• Self-attention：self顾名思义，计算自身序列中各位置与其他各位置的注意力，V来自自身。
• Target-Attention：计算自己和其他内容的注意力，V来自其他内容。
• Self-Attention 可以通过两个位置一步attention计算，远距离学习知识依赖和语序结构。
• RNN/LSTM：距离越远，信息损耗越大，有效提取捕获远可能性越小。

Attention vs 全连接

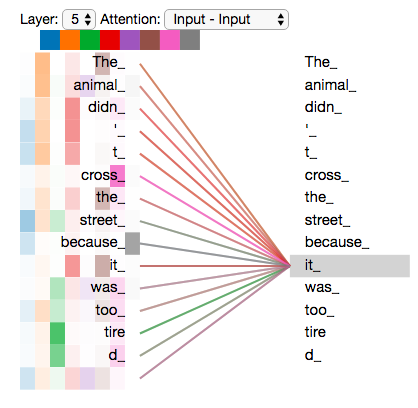
• 👁️Attention：有锚点👍
  • 有Query和Key，有Value。Query作为一个锚点计算attention score后做加权。
  • 比喻：左手拿白色小球，右手从袋子抓球，抓出来和左手做对比
• 全连接层：🈚️锚点
  • 无Query和Key，只有一个Value。最后给每个v一个权重做加权。
  • 比喻：在袋子里凭记忆和感觉随便抓一个球出来。

Attention 变体

• 最早期的Attention、Hard Attention等。
• Muliti-Head Attention：使用多组QKV生成多个Z，拼接乘大矩阵，得融合Z，再给FFN。
  • 学习不同表征，识别不一样的模式，增强模型表达能力
• Relative Position Encoding：使用相对位置编码引入位置信息

Attention 解码详细推导

参考文章

• 大模型推理加速：看图学KV Cache
• KV Cache技术笔记

Attention 推导

符号定义

• 假设dim=$d_k$，部分公式省略缩放、softmax、向量转置等。
• ${\text{Attn}}_{stepi}(Q,K,V)$：第i步的完整Attention矩阵
• ${\text{Attn}}_i(Q,K,V)$：attention矩阵的第i行

Step=1，共1行

• 第1行：$Att{n}_1(Q,K,V)=\text{softmaxted}(Q_1{K}_1^T){\overrightarrow{V}}_1=(Q_1{K}_1^T){\overrightarrow{V}}_1$

$$\begin{array}{ll}{\text{Attn}}_{step1}(Q,K,V)& =\text{softmax}(\frac{Q_{1}K{1}^T}{\sqrt{d_k}})\times V_1=\left[\begin{array}{c}{Q}_1\end{array}\right]\cdot \left[\begin{array}{c}{K}_1^{\mathrm{\top }}\end{array}\right]\cdot \left[\begin{array}{c}{V}_1\end{array}\right]\\ & =[\text{softmax}(Q_1{K}_1^T)\times \overrightarrow{V_1}]\\ & =[{\text{Attn}}_1(Q,K,V)]\end{array}$$

Step=2，共2行

• 第1行：$Att{n}_1(Q,K,V)=(Q_1{K}_1^T){\overrightarrow{V}}_1$，step1已算过
• 第2行：$Att{n}_2(Q,K,V)=(Q_2{K}_1^T){\overrightarrow{V}}_1+(Q_2{K}_2^T){\overrightarrow{V}}_2$

$$\begin{array}{ll}Att{n}_{step2}(Q,K,V)& =\left[\begin{array}{c}{Q}_1\\ Q_2\end{array}\right]\cdot \left[\begin{array}{cc}{K}_1& K_2\end{array}\right]\cdot \left[\begin{array}{c}{V}_1\\ V_2\end{array}\right]\\ & =\left[\begin{array}{cc}{Q}_1{K}_1^T& \underset{Q1\mathrm{不}\mathrm{能}\mathrm{看}\mathrm{见}K2}{\underbrace{Q_1{K}_2^T}}\\ Q_2{K}_1^T& Q_2{K}_2^T\end{array}\right]\cdot \left[\begin{array}{c}{V}_1\\ V_2\end{array}\right]=\underset{\mathrm{被}mask\mathrm{掉}，softmax\mathrm{为}\mathrm{负}\mathrm{无}\mathrm{穷}}{\underbrace{\left[\begin{array}{cc}{Q}_1{K}_1^T& -\mathrm{\infty }\\ Q_2{K}_1^T& Q_2{K}_2^T\end{array}\right]}}\cdot \left[\begin{array}{c}{V}_1\\ V_2\end{array}\right]\\ & =\underset{\mathrm{过}\mathrm{了}softmax\mathrm{和}\mathrm{缩}\mathrm{放}，\mathrm{简}\mathrm{写}}{\underbrace{\left[\begin{array}{cc}{Q}_1{K}_1& 0\\ Q_2{K}_1& Q_2{K}_2\end{array}\right]}}\cdot \left[\begin{array}{c}{V}_1\\ V_2\end{array}\right]\\ & =\left[\begin{array}{c}{Q}_1{K}_1^T{V}_1\\ Q_2{K}_1{V}_1+Q_2{K}_2{V}_2\end{array}\right]=\left[\begin{array}{c}Att{n}_1(Q,K,V)\\ Q_2{K}_1^{\mathrm{\top }}{V}_1+Q_2{K}_2^{\mathrm{\top }}{V}_2\end{array}\right]\end{array}$$

Step=3, 共3行

• 第1行：$Att{n}_1(Q,K,V)=(Q_1{K}_1^T)V_1$，第1步已算过
• 第2行：$Att{n}_2(Q,K,V)=(Q_2{K}_1^T)V_1+(Q_2{K}_2^T)V_2$，第2步已算过
• 第3行：$Att{n}_3(Q,K,V)=(Q_3{K}_1^T)V_1+(Q_3{K}_2^T)V_2+(Q_3{K}_3^T)V_3$，第3步算第3行

结论

• 每一步都存在大量冗余，第i步，只需要计算第i行即可，前i-1行都已经计算过

• 矩阵中，第k行只和$Q_k$相关，和其余位置的Q无关。

  • $Q_k$会和前面的每一对$K_i,V_i$做attention计算，来计算当前行。

• 解码$x_k$，只需输入字符$x_{k-1}$即可。

几个重点思考(降维/dk等)

重要思考

1、Self-Attention Padding 做 Mask

• $Q\cdot K$ ，需要对padding部分置为$-\mathrm{\infty }$负无穷，再过Softmax才会为0。

2、Transformer Multi-Head Attention 要对head 进行降维

• 输入向量维度为$d$，需要降维到 $d^{\prime }$（远小于d），主要是为了降低计算复杂度
• 时间复杂度：$o(d^2)、o(h{d}^2)\to o({d^{\prime }}^2)、o(h{d^{\prime }}^2)$

3、维度和点击的关系

• $q,k$向量 维度d越大，点积值$q\cdot k$越大，点积属于均值0、方差$d$的正态分布。

  $$E(q\cdot k)=0,D(q\cdot k)=d$$

• 方差的性质

  $$D(cx)=c^{2}D(x),D(c+x)=D(x)。c\mathrm{为}\mathrm{常}\mathrm{数}$$

3、深入理解$\sqrt{d_k}$缓解梯度爆炸问题

• Attention计算过程：内积$QK$后 -> softmax。softmax主要入参是$e^{qk}$。

• 如果不进行缩放：

  • softmax入参在$[e^{-3\sqrt{d}},e^{3\sqrt{d}}]$之间，会很大或很小
    • 导致注意力权重 接近one-hot分布
    • 饱和区梯度消失：x值继续变大，y几乎不变

• 因此：QK后才除以$\sqrt{d_k}$

  • 使得softmax入参在$[e^{-3},e^3]$之间，不大也不小

• 数学思路

  • $q\cdot k$ 除以$\sqrt{d}$，抵消掉，由0-d正态分布，又回到0-1正态分布。
  $$E(q\cdot k)=0,D(q\cdot k)=d\Rightarrow D(\frac{q\cdot k}{\sqrt{d}})=\frac{q\cdot k}{(\sqrt{d}{)}^2}=1$$
  • 方差为1，有效控制点积结果发散，应对了梯度消失问题。

注意力算法优化(降低时间复杂度)

线性注意力

参考文章

• 线性注意力简史：从模仿、创新到反哺

核心思想

线性注意力核心思想

背景

• 把FullAttention 复杂度$\text{O}(d{n}^2)$变为$\text{O}(n{d}^2)$，$O(n^2)$ 变成 $O(n)$，即平方复杂度变成线性复杂度。

核心思想

• 矩阵交换律，右乘，中间状态矩阵迭代计算，具体公式见下文。

优点

• 速度极快、内存占用小

缺点

• 性能效果损失，最新MiniMax-M2 已经由 Lighting Attention 切换回 FullAttention了。

线性注意力基本公式

线性注意力

线性注意力基本公式

• 交换位置，时间复杂度由$\text{o}(d{n}^2)$变为$\text{o}(n{d}^2)$，线性依赖于n。
  • 复杂度例子见上文 Softmax和Linear时间复杂度

$$\mathit{O}=\underset{{\mathbb{R}}^{n\times n}}{\underbrace{(\mathit{Q}{\mathit{K}}^{\mathrm{\top }})}}\underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{V}}}⟹\underset{{\mathbb{R}}^{n\times d}}{\underbrace{\mathit{Q}}}\underset{{\mathbb{R}}^{d\times d}}{\underbrace{({\mathit{K}}^{\mathrm{\top }}\mathit{V})}}$$

• 分量形式

  $${\mathit{o}}_t=\sum _{j=1}^t\underset{\mathrm{向}\mathrm{量}}{\underbrace{{\mathit{v}}_j}}\underset{\mathrm{标}\mathrm{量}}{\underbrace{({\mathit{k}}_j^{\mathrm{\top }}{\mathit{q}}_t)}}=\sum _{j=1}^t({\mathit{v}}_j{\mathit{k}}_j^{\mathrm{\top }}){\mathit{q}}_t=(\sum _{j=1}^t{\mathit{v}}_j{\mathit{k}}_j^{\mathrm{\top }}){\mathit{q}}_t={\mathit{S}}_t{\mathit{q}}_t$$
  • 各元素维度$${\mathit{v}}_j\in {\mathbb{R}}^{d\times 1}，{\mathit{k}}_j^{\mathrm{\top }}\in {\mathbb{R}}^{1\times d}，{\mathit{q}}_t\in {\mathbb{R}}^{d\times 1}\to {\mathit{k}}_j^{\mathrm{\top }}{\mathit{q}}_t\in {\mathbb{R}}^{1\times 1},{\mathit{S}}_t={\mathit{v}}_j{\mathit{k}}_j^{\mathrm{\top }}\in {\mathbb{R}}^{d\times d}$$

状态公式

• 记括号部分为${\mathit{S}}_t$，Casual形式的Attention可写成以${\mathit{S}}_t$为状态的线性RNN$${\mathit{o}}_t={\mathit{S}}_t{\mathit{q}}_t,{\mathit{S}}_t={\mathit{S}}_{t-1}+{\mathit{v}}_t{\mathit{k}}_t^{\mathrm{\top }}$$

$${\mathit{S}}_t=\sum _{j=1}^t{\mathit{v}}_j{\mathit{k}}_j^{\mathrm{\top }}$$

• 线性Attention：本质是一个cumsum，将所有历史信息 等权地叠加。

记忆遗忘及解决方法(RetNet/Minimax-01)

提示

现行Attention 记忆遗忘缺点

• 本质是cumsum，各历史信息同等权重叠加。
• 当叠加token足够多时，每个token的信息占比会变得很小。
• 仅靠固定大小矩阵 ${\mathit{S}}_t\in {\mathbb{R}}^{d\times d}$难以准确重建任意token，每个token的记忆会变得模糊不清。

RetNet/MiniMax-01：增加衰减因子

• 衰减因子$\gamma$：模型倾向于遗忘早期信息，就近原则

$${\mathit{o}}_t={\mathit{S}}_t{\mathit{q}}_t,{\mathit{S}}_t=\gamma \cdot {\mathit{S}}_{t-1}+{\mathit{v}}_t{\mathit{k}}_t^{\mathrm{\top }}$$

DFW/Mamba/Mamba2

• 把衰减因子$\gamma$推广为位置t的函数$\gamma (t)$$${\mathit{o}}_t={\mathit{S}}_t{\mathit{q}}_t,{\mathit{S}}_t=\gamma (t)\cdot {\mathit{S}}_{t-1}+{\mathit{v}}_t{\mathit{k}}_t^{\mathrm{\top }}$$

TestTimeTraining

Test Time Training

TTT 思想

• 把 $\mathit{K}\mathbf{,}\mathit{V}$视作语料对，根据语料训练模型，${\mathit{S}}_{\mathit{t}}$为模型参数

  $$({\mathit{k}}_1,{\mathit{v}}_1),({\mathit{k}}_2,{\mathit{v}}_2),\cdots ,({\mathit{k}}_t,{\mathit{v}}_t)$$

• 最后输出

  $${\mathit{o}}_t=\mathit{f}({\mathit{S}}_t,{\mathit{q}}_t)$$

TTT 实现的RNN

• 当前模型参数为${\mathit{S}}_{t-1}$，优化器接收到新数据$(k_t,v_t)$，更新模型参数为${\mathit{S}}_t$

  $${\mathit{o}}_t=f({\mathit{S}}_t,{\mathit{q}}_t),{\mathit{S}}_t={\mathit{S}}_{t-1}-{\eta }_t{\mathrm{\nabla }}_{S_{t-1}}\mathcal{L}(\mathit{f}({\mathit{S}}_t,{\mathit{q}}_t),v_t)$$

• RNN：把历史数据有效压缩到一个固定大小的State中，而模型参数正好是固定大小的。

• 类比

  • 压缩任务：RNN；解压器：模型$f$；压缩包：权重；压缩算法：SGD；压缩率：损失L

线性注意力主要工作

线性注意力主要工作

• MiniMax-Text-01, MiniMax M1
• Kimi Linear

Sparse Attention

参考文章

• Transformer综述（一）：稀疏注意力
• DeepSeek Native 稀疏注意力

核心思想

核心思想

背景

• 传统Softmax Attention，时间复杂度随长度二次方增加 $o(d{n}^2)$，不利于长度扩展。

稀疏注意力核心思想

• 假设
  • 一个token只需关注序列中少数几个关键位置，无需关注所有位置。
• 具体做法
  • 不计算完整 N×N的注意力矩阵，只计算一小部分稀疏位置的。
  • 只选择与Q相关的少量Token，来计算Query-Key注意力。

优点

• 在性能和效率之间取得平衡，复杂度可降低到$o(n\log n)$

传统稀疏注意力的缺点

• 实际效果并不好：加速不好、且缺乏预训练等。
• 具体见笔记 Native Sparse Attention ：稀疏注意力实际效果并不好

常见稀疏模式

常见稀疏模式

局部注意力 / Sliding Window

• 只关注邻近的几个词。

全局注意力 / Global Attention

• 预设一些全局节点，让所有词都与它们进行计算。

组合模式

• 巧妙结合压缩、选择、滑动窗口三种模式，比如 DeepSeek NSA 论文笔记

稀疏注意力主要工作

稀疏注意力主要工作

• DeepSeek NSA

注意力结构优化(提升推理效率)

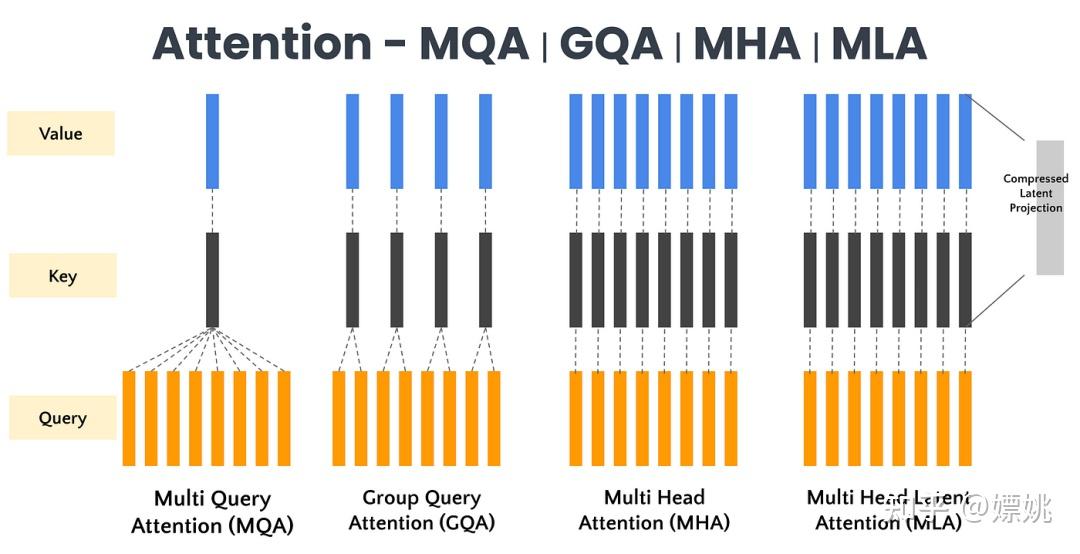
一图概览MHA+MQA+GQA+MLA

MHA + MQA + GQA + MLA

Multi-Head Attention

• 并行计算多个子空间QKV的注意力，提升模型表达能力。

Multi-Query Attention

• 所有Query共享一对K和V，减少KV参数，提升推理速度，优化$o(d{n}^2)$问题。

Group-Query Attention

• 在MHA和MQA中做折中，把Query分组，每组共享一对K和V，效果比MQA好、速度比MHA快。

Multi-Head Latent Attention

• 把KV联合压缩成一个 小的潜在向量，来解决KV缓存高的问题。压缩、缓存、重建三步。

Mulit-Head Attention(2017)

多头注意力

Multi-Head Attention

核心思想

• MHA，多组QKV，学习不同表征模式，增强模型能力，类似CNN多个卷积核

优点

• 多头关注不同部分，最终再融合 起来得更好效果。

• 如：对词向量维度512进行8头切割，每头输入维度为64，最后采用concat进行融合。

缺点

• 计算成本高

Multi-Query Attention(2019)

Multi-Query-Attention

核心思想

• 所有query共享同一个Key和Value 矩阵，每头仅保留Query参数，

优点

• 大大减少KeyValue参数，提升推理速度

缺点

• 但带来 精度损失。

Group-Query Attention(2023)

Grouped-Query Attention

核心思想

• query分为n组，每组共享Key和Value矩阵。
• 其实在MHA和MQA之间做折中。

优点

• 精度比MQA好，速度比MHA快。

Multi-Head Latent Attention(2024)

参考文章

• 彻底理解MLA（Multi-Head Latent Attention）
• Multi-head Latent Attention多头潜在注意力机制
• paper: DeepSeekV2

Multi-Head Latent Attention

问题

• MHA计算复杂度高 $O(d{n}^2)$，
• MHA推理长序列时，KV缓存高、显存压力大。

核心思想: 低秩KeyValue联合压缩

• 压缩
  • 不直接计算存储完整的K和V，而是压缩成一个维度很小的latent vector
• 缓存
  • 推理时，缓存非常小的潜在向量，而非原始KV
• 重建
  • 在计算注意力时，从缓存的latent vector中，重建出原始的Key和Value。

优点

• 大幅减少KV缓存：与DeepSeek 67B比，KV缓存减少93.3%
• 推理性能提升：最大生成吞吐量提升5.76倍
• 相比MQA/GQA，性能还有提升

实现优化(解决硬件效率问题)

Flash Attention

Flash Attention

• 目前最高效的注意力实现
• 核心思想：利用GPU的SRAM，将连续的内存块，加载进来进行计算，最大化硬件利用率。

GPU 硬件限制

GPU 硬件限制

• GPU - SRAM：很小很快，20MB、19TB/s (吞吐量)
• GPU - HBM：GPU显存大小，大但慢，80GB、1.5TB/s
• CPU - DRAM：CPU内存，很大但很慢， 1TB、12GB/s

Softmax Tiling

参考文章：FlashAttention中的softmax快分块计算详解

Softmax Tiling

• 数值稳定

  • 背景：避免数值$e^{x_i}$ 过大溢出，
  • 方法：每个元素都减去最大值得$e^{x_i-max(x)}$
  • 效果：$e^{x_i-max(x)}$ 在[0,1]区间。softmax结果和原softmax一致

• 分块计算softmax：

  • 把X分为多个块，各块单独计算最大值、softmax分子、softmax分母
  • 根据各块信息，计算全局分母；再更新各自分子，得全局分子。

Flash Attention 算法

Flash Attention 算法

• 主要目标：避免从GPU-HBM中读取和写入注意力矩阵。
• 计算softmax不需要全局信息
  • 把输入分块，以分块增量方式计算softmax，即 softmax tiling算法。
• 反向传播不存储中间attention矩阵($N^2$)，只存储softmax归一化系数。
  • 标准Attention：需要把过程中的S、P写入HBM中，矩阵大小和输入序列长度有关，非常大
  • FlashAttention：不使用中间注意力矩阵，通过存储归一化因子来减少HBM内存的消耗。
• 算法流程，具体见论文。
  • 简单讲：每次只计算一个block的只，通过多轮双for循环完成注意力计算。