位置编码背景

简单总结

不同于RNN/CNN模型，Transformer模型必须加入位置编码，纯粹靠attention是无法捕捉顺序信息的，即无法区分不同位置的token。

位置编码总结

• 绝对位置编码
  • 优点：实现简单，不用训练，高效计算。
  • 缺点：没有外推性。
• 相对位置编码
  • 优点：直接体现相对位置，效果更好。具有一定外推性。
  • 缺点：模型计算复杂，长序列仍然有外推性问题。
• RoPE(旋转位置编码)
  • 优点：结合了绝对和相对位置的优点。
  • 缺点：实现复杂，理论上外推性更好，但可能仍然存在外推问题。没训练过，效果不好。

位置编码动机

注意力权重

无位置信息时

• 缺点：注意力权重和位置无关，无论q和k的位置如何变化，注意力权重都保持不变。
• 直觉：希望两个词位置相近时，注意力权重大；相距较远时，注意力权重小。

$${\alpha }_{m,n}=\frac{\exp ({\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_n)}{\sum _{j=1}^N\exp (\frac{{\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_j}{\sqrt{d_k}})}$$

引入位置信息的注意力权重

• 为向量$q_m$ 注入位置信息

  $$q_m=f(q,m)$$

• 注意力权重：和位置相关

$${\alpha }_{m,n}=\frac{\exp (f(q,m{)}^{\mathrm{\top }}f(k,n))}{\sum _{j=1}^N\exp (\frac{f(q,m{)}^{\mathrm{\top }}f(k,j)}{\sqrt{d_k}})}$$

绝对位置编码

早期笔记：Transformer-位置编码

三角函数绝对位置编码

绝对位置编码

0. 核心思想

• 直接为输入$x_k$向量 增加一个位置向量$p_k$

$$x_k=x_k+p_k,p_k\text{为位置编码，与}\text{位置k}\text{有关}，$$

1. 可训练式

• 定义：把位置向量作为可训练参数，如$n\ast d$维度。
• 缺点：没有外推性，难处理超过最大长度n的位置信息

2. 三角式

• 定义：$p_k$中第$2i$和$2i+1$ 各位置的值，分别由sin和cos函数来定义。

$$\begin{array}{ll}{\mathit{p}}_{k,2i}& =\sin (\frac{k}{{10000}^{2i/d}})\\ {\mathit{p}}_{k,2i+1}& =\cos (\frac{k}{{10000}^{2i/d}})\end{array}$$

• 特点：

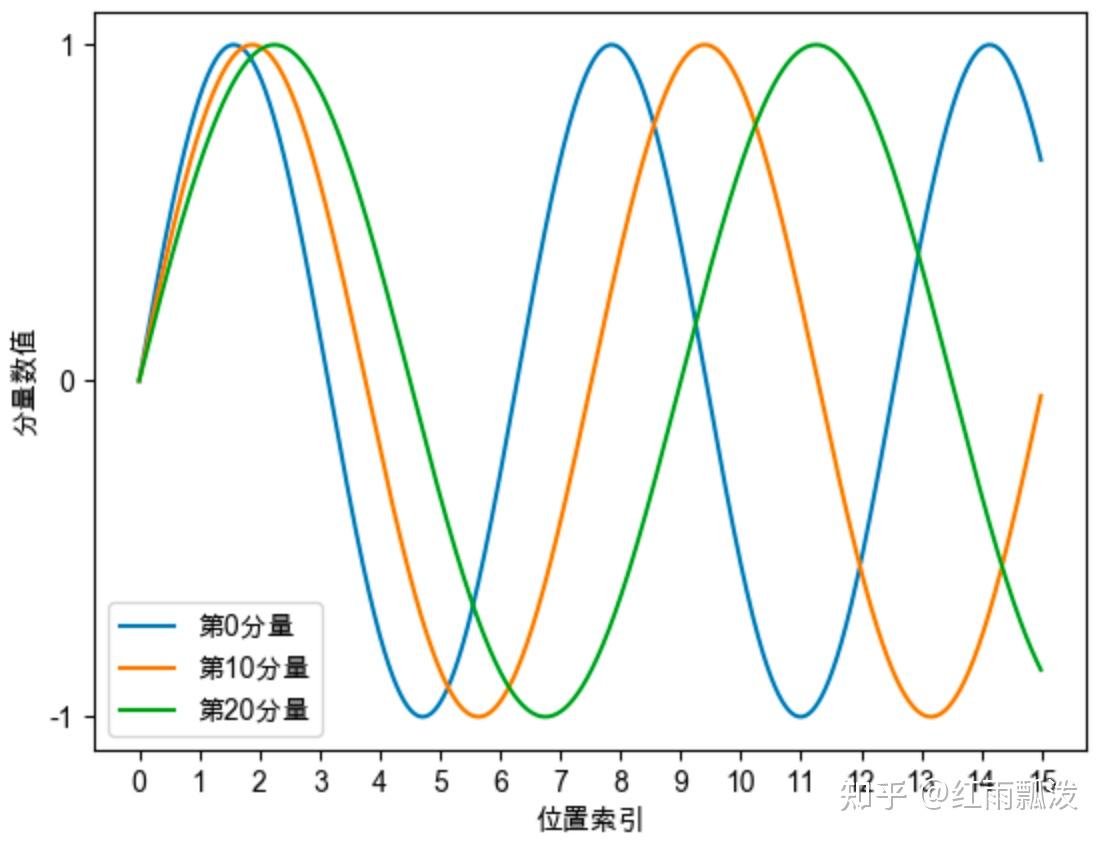
  • 每个分量都是三角函数，每个分量数值都具有周期性。
  • 越靠后的分量，波长越长，频率越低。
  • 远程衰减性质：
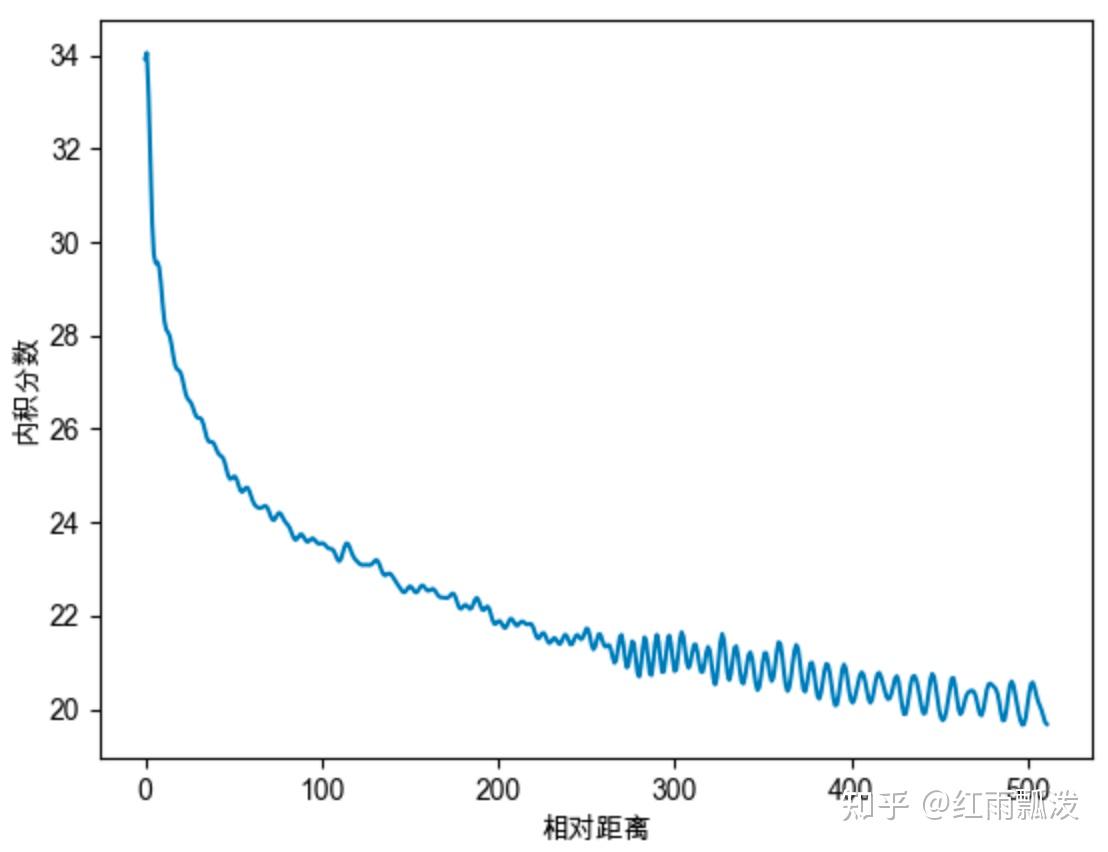
    • 两个相同的词向量，相对位置位置越近，内积向量分数越大；位置越远，分数越小。

• 优点：三角函数有一定外推性，不用训练。

• 缺点：但现在很少看到这种绝对位置编码的工作。

3. 递归式

• 定义：通过递归计算位置编码，$p_{k+1}=f(p_k)$，示例论文。
• 优点：具有较好外推性
• 缺点：牺牲并行性，计算不足

周期性：

远程衰减：

绝对位置编码注意力公式

Softmax Attention 公式 笔记

绝对位置编码Attention 公式

💥计算$i$和$j$的attention

• 其中$q、k、v、p$均为向量。

$$\begin{array}{l}{q}_i=(x_i+p_i)W_Q=f_q(x_i,i)\\ k_j=(x_j+p_j)W_K=f_k(x_j,j)\\ v_j=(x_j+p_j)W_V=f_v(x_j,j)\\ {\alpha }_{i,j}=\text{softmax}(q_i{k}_j^{\mathrm{\top }})\\ o_i=\sum _j{\alpha }_{i,j}{v}_j\end{array}$$

⭐$q_i{k}_j^T$展开项

• 后续相对位置编码都是基于此修改

$$\begin{array}{ll}{\mathit{q}}_{\mathit{i}}{\mathit{k}}_{\mathit{j}}^{\mathbf{\top }}& =(x_i+p_i)W_Q\cdot [(x_j+p_j)W_K{]}^{\mathrm{\top }}\\ & =(x_i+p_i)W_Q\cdot W_K^T(x_j+p_j{)}^T\\ & =(x_i{W}_Q+p_i{W}_Q)\cdot (W_K^T{x}_j^T+W_K^T{p}_j^T)\\ & =\underset{\mathrm{输}\mathrm{入}i\mathrm{和}\mathrm{输}\mathrm{入}j}{\underbrace{x_i{W}_Q{W}_K^T{x}_j^{\mathrm{\top }}}}+\underset{\mathrm{输}\mathrm{入}i\mathrm{和}\mathrm{位}\mathrm{置}j}{\underbrace{x_i{W}_Q{W}_K^T{p}_j^{\mathrm{\top }}}}+\underset{\mathrm{位}\mathrm{置}i\mathrm{和}\mathrm{输}\mathrm{入}j}{\underbrace{p_i{W}_Q{W}_K^T{x}_j^{\mathrm{\top }}}}+\underset{\mathrm{位}\mathrm{置}i\mathrm{和}\mathrm{位}\mathrm{置}j}{\underbrace{p_i{W}_Q{W}_K^T{p}_j^T}}\end{array}$$

传统相对位置编码

相对位置编码 核心思想

• 在计算attention时，考虑当前位置和目标位置的相对距离，不建模输入位置的全局信息
• NLP任务更适合相对位置编码👍。

相对位置编码

🧠 ​1、经典相对位置编码核心思想

• 核心

  • 从绝对位置attention公式出发
  • 去掉$p_j$及复杂内容, 由二元位置向量$R_{i,j}$来代替，主要在softmax和v加权里变换。

• 💥相对位置$R_{i,j}$

  • 只依赖相对距离 $i-j$。
  • Clip裁切：把相对距离缩短至有限范围。PPO-Clip 笔记
  • ${\mathit{p}}_{\mathit{k}}\mathbf{,}{\mathit{p}}_{\mathit{v}}$：位置向量

$$\begin{array}{l}{R}_{i,j}^K={\mathit{p}}_{\mathit{k}}[\text{clip}(i-j,p_{min},p_{max})]\\ R_{i,j}^V={\mathit{p}}_{\mathit{v}}[\text{clip}(i-j,p_{min},p_{max})]\end{array}$$

• 优点
  • 只需要有有限个位置向量，即可表示任意相对位置(因为进行了截断) 👍

2、XLNet式相对位置编码

• 核心
  • 从公式${\mathit{q}}_{\mathit{i}}{\mathit{k}}_{\mathit{j}}^{\mathbf{\top }}$ 展开，相对位置向量$R_{i-j}$替换$p_j$， 可训练向量$u,v$替换2个$p_i$
  • $R_{i-j}$ 不做截断，用了Sinusoidal式的生成方案。
  • $v_j$加权时 不再需要位置偏置，直接是$o_i=\sum _j{\alpha }_{i,j}{x}_j{W}_v$
  • 后期工作相对位置只在attention权重上计算，不在v上了。

3、T5

• 核心：从${\mathit{q}}_{\mathit{i}}{\mathit{k}}_{\mathit{j}}^{\mathbf{\top }}$ 展开出发做简化。

  • 认为输入和位置当解耦不做交互，直接删掉很多项

  • 增加相对位置编码 可训练参数

  $$q_i{k}_j^T=x_i{W}_Q{W}_K^T{x}_j+{\beta }_{i,j}$$

• ${\beta }_{i,j}$不做$i-j$截断，做分桶处理，相对位置$i-j$对应$f(i-j)$。

  • 近的位置使用独立精细编码，越远越共用一个位置编码。

4、Deberta式

• 核心：从${\mathit{q}}_{\mathit{i}}{\mathit{k}}_{\mathit{j}}^{\mathbf{\top }}$ 出发，扔掉第4项，保留2、3项并改为相对位置编码。

旋转位置编码

参考文章

• 图解RoPE旋转位置编码及其特性
• 十分钟读懂旋转编码 RoPE

RoPE 动机

RoPE 动机

• 通过绝对位置方式实现相对位置编码 ，综合了绝对和相对的优点😍

• 希望$q_m\cdot k_n$ 点积，自动带有相对位置信息 $m-n$

  • 只需把点积变成q,k,m-n的函数即可。
  • 找到一个函数 $f(q,m)$，为向量$q$增加绝对位置信息m，得到$q_m$，同时使下式成立即可
  $$q_m^{\mathrm{\top }}\cdot k_n=f(q,m)\cdot f(k,n)=g(q,k,m-n)$$

• 作者通过复数完成求解。

旋转矩阵性质

旋转矩阵

旋转矩阵

• 二维空间，存在旋转矩阵$M(\theta )$

• 二维向量 左乘旋转矩阵，该向量即可实现弧度为$\theta$的逆时针旋转操作。

  $$M(\theta )=\left(\begin{array}{ll}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$$

旋转示例

• 二维向量$(1,0)$

  • 逆时针旋转45度：即弧度$\frac{\pi }{4}$，得到新向量$(\sqrt{2}/2,\sqrt{2}/2)$

  • 通过旋转矩阵计算：同样得到新向量$(\sqrt{2}/2,\sqrt{2}/2)$，模长仍为1，保持不变。

  • 正弦、余弦、正切

    $$\left(\begin{array}{ll}\cos \frac{\pi }{4}& -\sin \frac{\pi }{4}\\ \sin \frac{\pi }{4}& \cos \frac{\pi }{4}\end{array}\right)\cdot \left(\begin{array}{l}1\\ 0\end{array}\right)=\left(\begin{array}{l}\cos \frac{\pi }{4}\\ \sin \frac{\pi }{4}\end{array}\right)=\left(\begin{array}{l}\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}\end{array}\right)$$

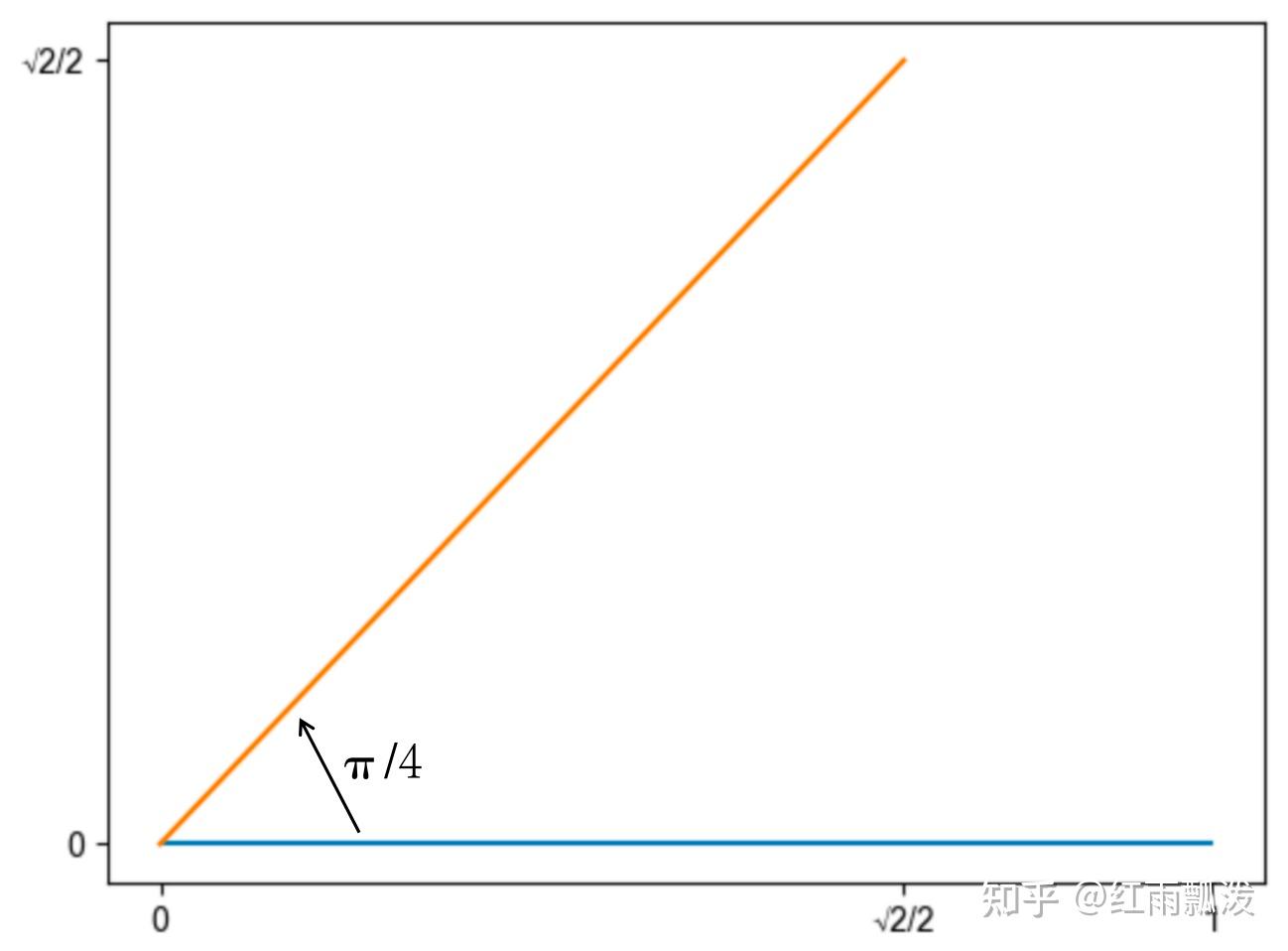
二维位置编码

二维旋转矩阵-绝对位置信息-相对编码

旋转矩阵增加绝对位置信息

• 假设词向量只有2维，得到位置编码函数，$\theta$为常数。

$$f(q,m)=R_m\cdot q=\underset{\text{旋转矩阵}}{\underbrace{\left(\begin{array}{ll}\cos m\theta & -\sin m\theta \\ \sin m\theta & \cos m\theta \end{array}\right)}}\cdot \underset{q\mathrm{向}\mathrm{量}}{\underbrace{\left(\begin{array}{l}{q}_0\\ q_1\end{array}\right)}}$$$$f(k,n)=R_n\cdot k=\underset{\text{旋转矩阵}}{\underbrace{\left(\begin{array}{ll}\cos n\theta & -\sin n\theta \\ \sin n\theta & \cos n\theta \end{array}\right)}}\cdot \underset{k\mathrm{向}\mathrm{量}}{\underbrace{\left(\begin{array}{l}{k}_0\\ k_1\end{array}\right)}}$$

• 只要把向量旋转 $m\theta$弧度，就能对向量增加 绝对位置信息m
  • 只要把向量旋转某个角度，就能对向量，增加绝对位置信息

点积自动具有相对位置

• 通过推导可知

  • 点积自动带有相对位置信息 m-n，通过绝对编码方式，实现了相对位置编码
  $$q_m\cdot k_n=f(q,m)\cdot f(k,n)=q^{\mathrm{\top }}{R}_{n-m}k$$
  • 详细推导过程如下：三角函数两角和差公式

$$\begin{array}{ll}{q}_m\cdot k_n& =f(q,m)\cdot f(k,n)\\ & =(R_m\cdot q{)}^{\mathrm{\top }}\cdot (R_n\cdot k)=q^{\mathrm{\top }}{R}_m^{\mathrm{\top }}\cdot R_{n}k\\ & =q^{\mathrm{\top }}{\left[\begin{array}{ll}\cos m\theta & -\sin m\theta \\ \sin m\theta & -\cos m\theta \end{array}\right]}^{\mathrm{\top }}\cdot \left[\begin{array}{ll}\cos n\theta & -\sin n\theta \\ \sin n\theta & -\cos n\theta \end{array}\right]k\\ & =q^{\mathrm{\top }}\left[\begin{array}{ll}\cos m\theta & \sin m\theta \\ -\sin m\theta & \cos m\theta \end{array}\right]\cdot \left[\begin{array}{ll}\cos n\theta & -\sin n\theta \\ \sin n\theta & \cos n\theta \end{array}\right]k\\ & =q^{\mathrm{\top }}\left[\begin{array}{ll}\cos m\theta \cos n\theta +\sin m\theta \sin n\theta & -\cos m\theta \sin n\theta +\sin m\theta \cos n\theta \\ -\sin m\theta \cos n\theta +\cos m\theta \sin n\theta & \sin m\theta \sin n\theta +\cos m\theta \cos n\theta \end{array}\right]k\\ & =q^{\mathrm{\top }}\left[\begin{array}{ll}\cos (m-n)\theta & \sin (m-n)\theta \\ \sin (n-m)\theta & \cos (m-n)\theta \end{array}\right]k\\ & =q^{\mathrm{\top }}\left[\begin{array}{ll}\cos (n-m)\theta & -\sin (n-m)\theta \\ \sin (n-m)\theta & \cos (n-m)\theta \end{array}\right]k\\ & =q^{\mathrm{\top }}{R}_{n-m}k\end{array}$$

旋转示例

• 二维向量$q=(1,0)$，设$\theta =1$常数
• 当位置位于0/1/2/3时，只需旋转0/1/2/3弧度，即可赋予绝对位置信息。
• 只需对向量进行旋转，即可赋予绝对位置信息。

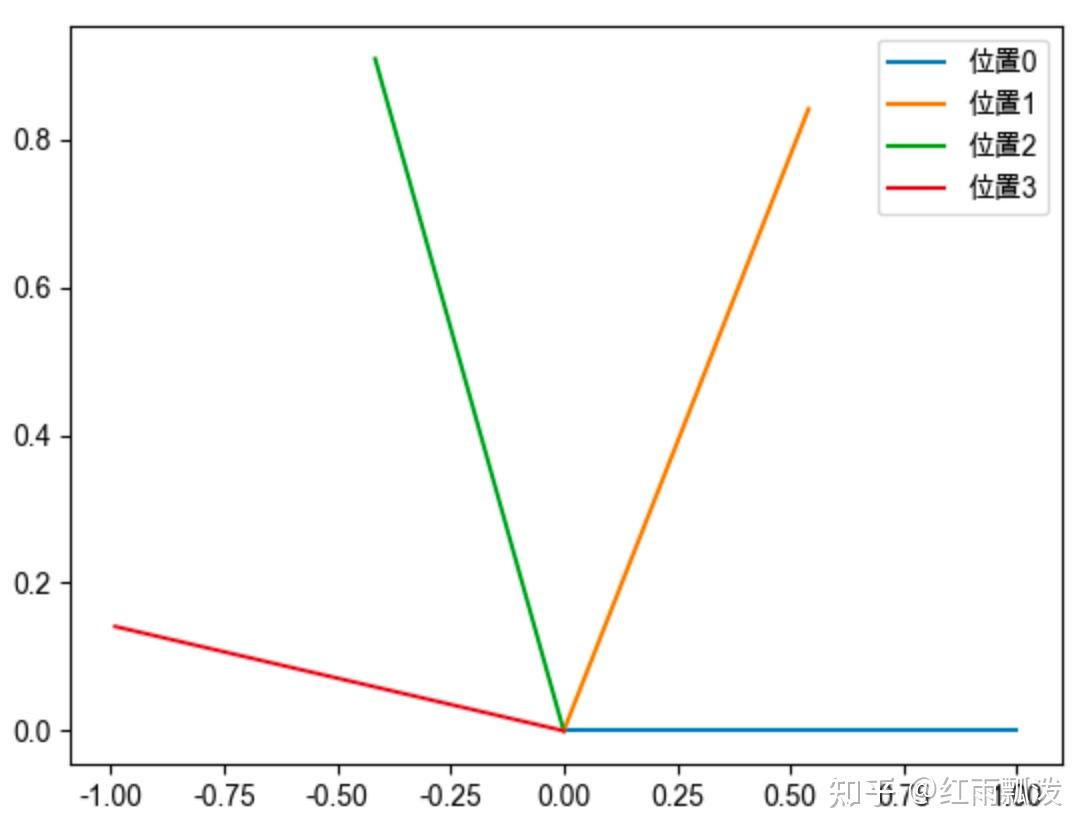
多维位置编码

推广到多维

高维旋转矩阵

• 把高维向量，两两一组，分别旋转。

• 把向量q中的d个分量，分成d/2组，每组视为一个二维向量，分别旋转。

  $$f(q,m)=R_m\cdot q=\left(\begin{array}{lllllll}\cos m\theta & -\sin m\theta & 0& 0& \cdots & 0& 0\\ \sin m\theta & \cos m\theta & 0& 0& \cdots & 0& 0\\ 0& 0& \cos m\theta & -\sin m\theta & \cdots & 0& 0\\ 0& 0& \sin m\theta & \cos m\theta & \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \\ 0& 0& 0& 0& \cdots & \cos m\theta & -\sin m\theta \\ 0& 0& 0& 0& \cdots & \sin m\theta & \cos m\theta \end{array}\right)\cdot \left(\begin{array}{l}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right)$$

增加远程衰减特性

远程衰减性

背景

• $\theta$如果是1个固定常量，会导致qk内积，随相对距离增加，内积分数呈震荡特性，缺乏远程衰减特性。

核心思想

• 借助三角函数，为旋转矩阵每个分组的$\theta$，设置单独常量，${\theta }_i={10000}^{-2i/d}$

• 当向量q位于位置m时，只需要把第i组分量，旋转$m{\theta }_i$弧度，即可得到具有绝对位置信息的向量$q_m$

  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}$$

• 高维旋转矩阵

$$R_m\cdot q=\left(\begin{array}{lllllll}\cos m{\theta }_0& -\sin m{\theta }_0& 0& 0& \cdots & 0& 0\\ \sin m{\theta }_0& \cos m{\theta }_0& 0& 0& \cdots & 0& 0\\ 0& 0& \cos m{\theta }_1& -\sin m{\theta }_1& \cdots & 0& 0\\ 0& 0& \sin m{\theta }_1& \cos m{\theta }_1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& \\ 0& 0& 0& 0& \cdots & \cos m{\theta }_{d/2-1}& -\sin m{\theta }_{d/2-1}\\ 0& 0& 0& 0& \cdots & \sin m{\theta }_{d/2-1}& \cos m{\theta }_{d/2-1}\end{array}\right)\cdot \left(\begin{array}{l}{q}_0\\ q_1\\ q_2\\ q_3\\ ⋮\\ q_{d-2}\\ q_{d-1}\end{array}\right)$$

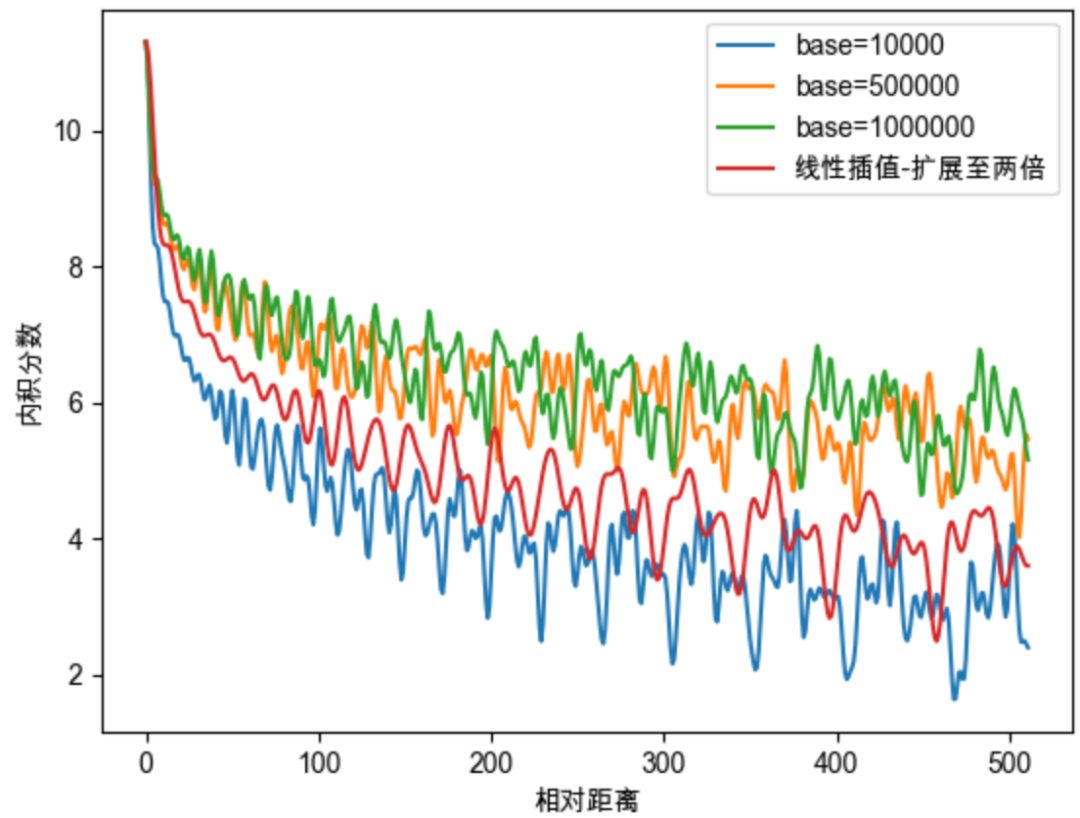
Base值10000的影响

• base的不同取值会影响注意力远程衰减的程度
  • base=1：失去衰减特性，太小base会破坏注意力远程衰减性质
  • base=1或100：注意力分数不再随相对位置增大，而呈震荡下降的趋势
  • base>500时：随base提升，远程衰减程度，会逐渐削弱

远程衰减特性：随相对距离变大、内积分数变小。

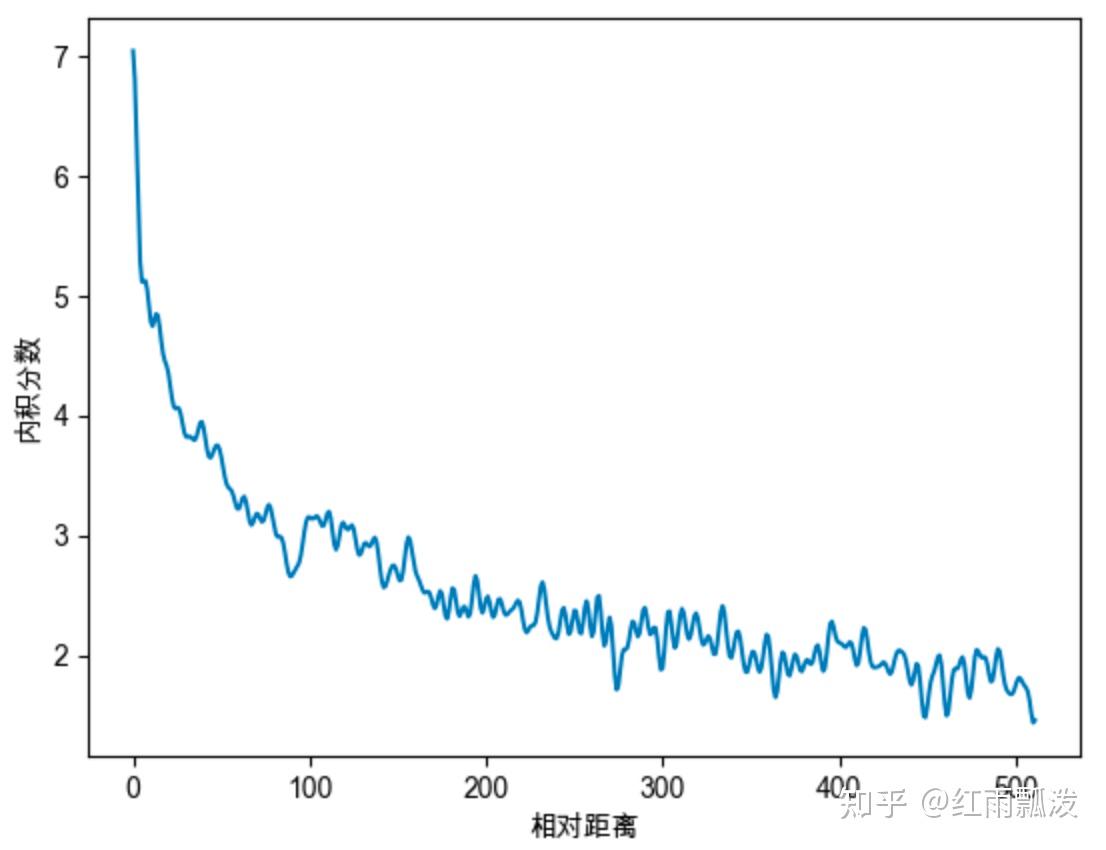
不同base对衰减特性的影响

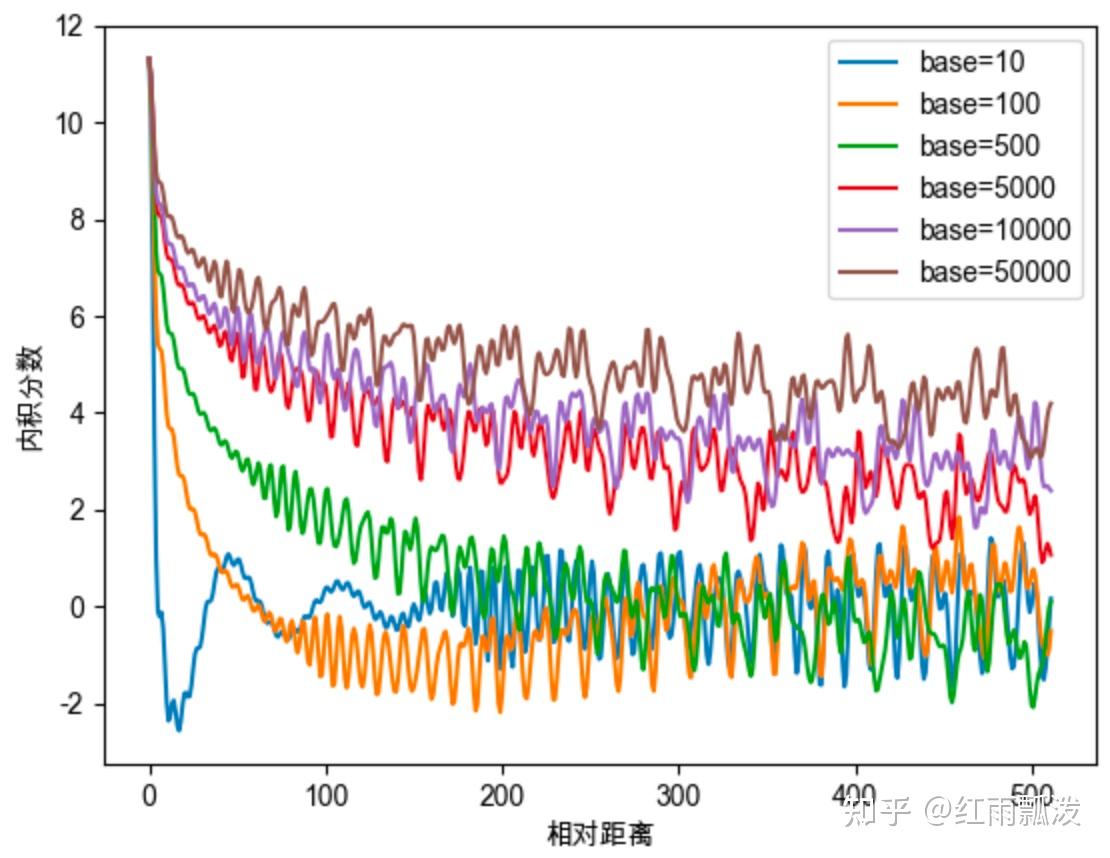
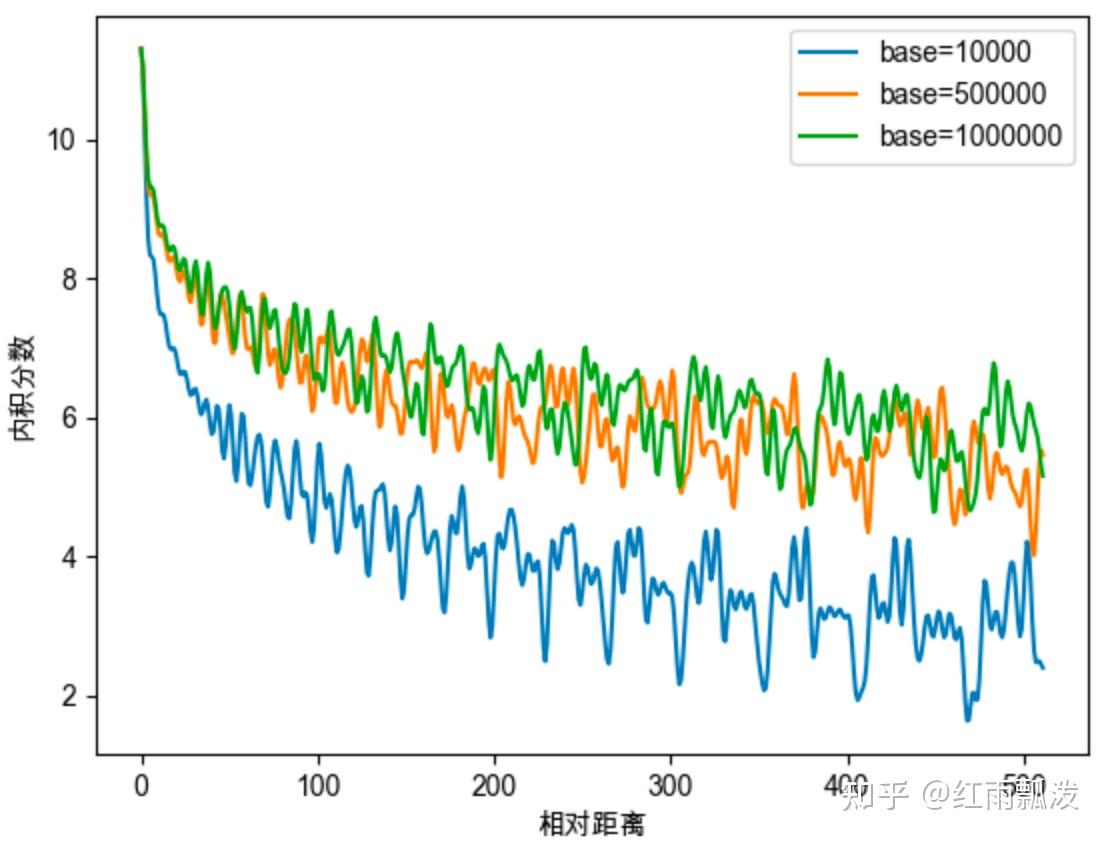
高低频分量概念

高低频分量

旋转角度和位置的关系

• RoPE旋转角度 随位置m和组别i 变化。旋转$m{\theta }_i$弧度。

  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}$$

• 对第i组分量，位置每增加1，旋转角度增加 ${\theta }_i$，角频率

高低频分量

• 高频分量
  • 分组越靠前，组别i越小，角频率 ${\theta }_i={\text{base}}^{-2i/d}$ 越大，$m{\theta }_i$ 旋转得越快。
• 低频分量
  • 分组越靠后，组别i越大，角频率 ${\theta }_i={\text{base}}^{-2i/d}$ 越小，$m{\theta }_i$ 旋转得越慢。

RoPE 特点

RoPE 特点

1. 具有远程衰减特性

• 随相对距离变大、内积分数变小。

2. 旋转弧度，随着位置增加而线性增加。

• 当位置位于0/1/2/3时，只需旋转0/1/2/3弧度，即可赋予绝对位置信息。$$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}$$

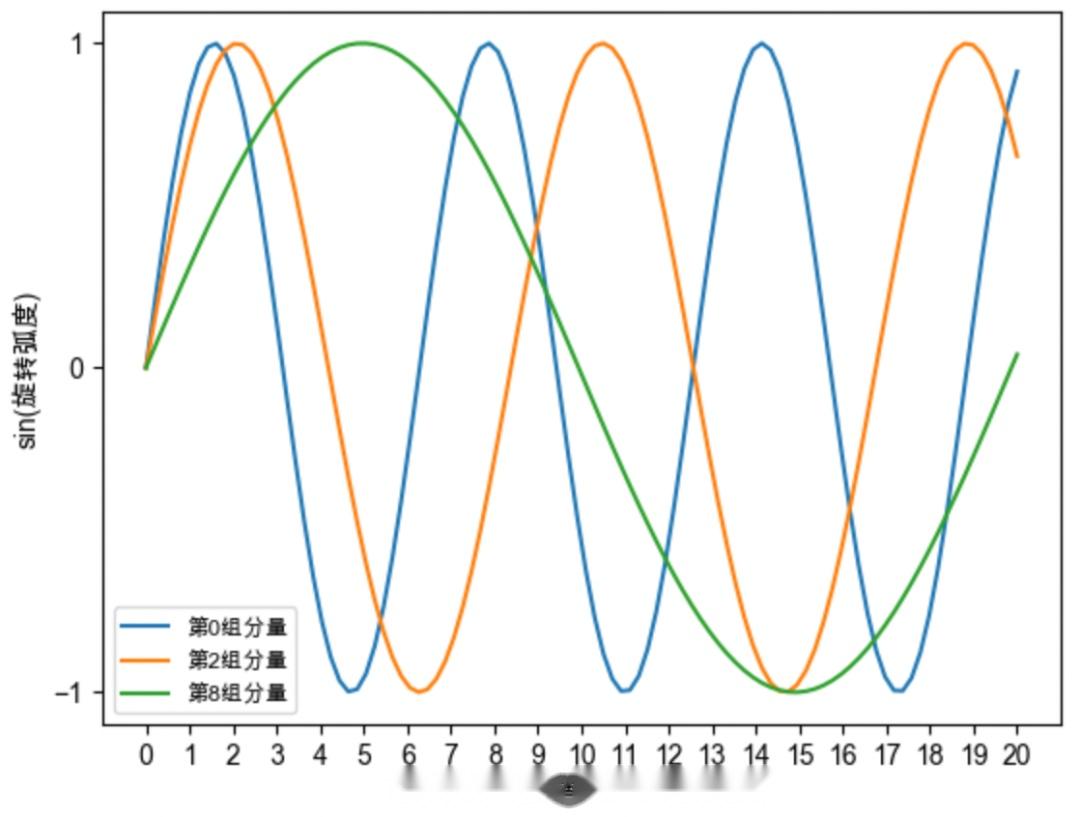
3. 每组分量的旋转具有周期性；分组越靠后，旋转速度越慢

• 旋转一圈的弧度是$2\pi$，具有周期性。

• 分组越靠前，旋转速度越快。

• 分组越靠后，旋转速度越慢，正弦的周期越大、频率越低。

  • 比如：位置500，第0组分量已旋转500弧度，第8组分量仅旋转158弧度。
  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}$$$$500{\theta }_0=500\cdot {\text{10000}}^{-0/d}=500$$$$500{\theta }_8=500\cdot {\text{10000}}^{-16/d}=158$$

第0组分量，旋转500弧度，但第8组，仅旋转158弧度。弧度和角度

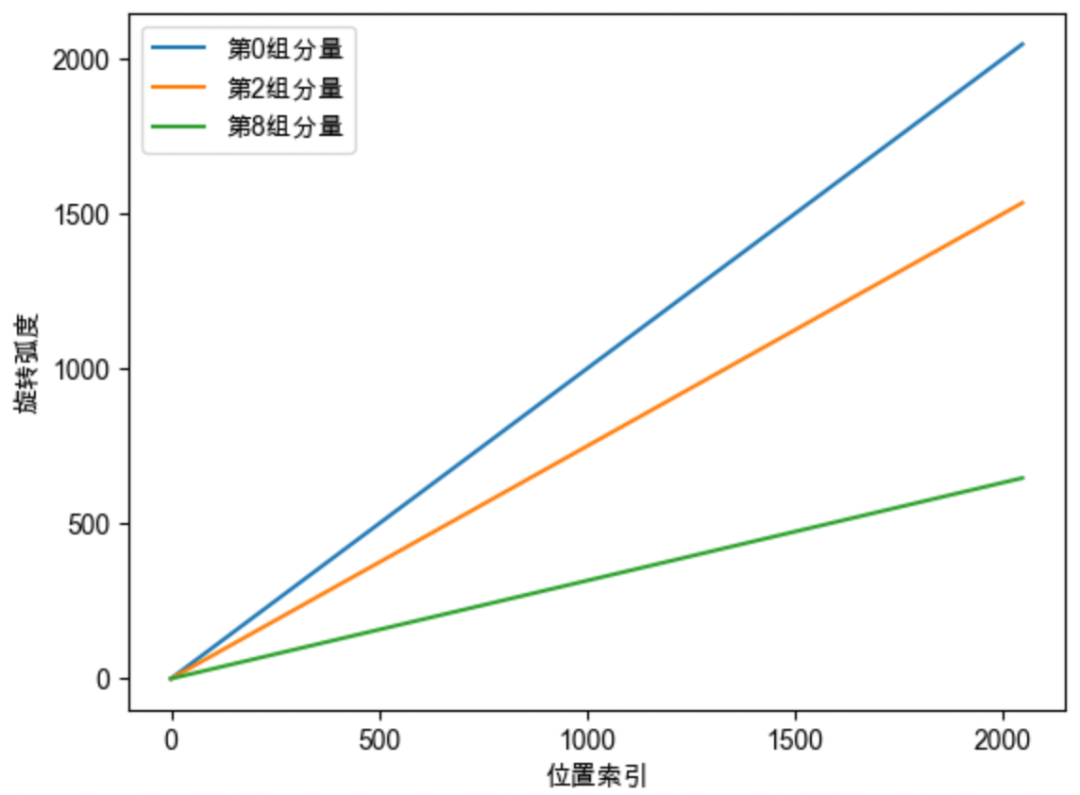
分组越靠后，旋转速度越慢，正弦周期越大、频率越低。第8组周期大、第0组周期小。

Rope 优缺点

RoPE 优点

• 输入向量，具有绝对位置信息；内积，自带相对位置信息。
  • 真正的位置编码
• 具有远程衰减特性
  • 两个固定向量，相对距离越远，内积值越小
  • 通过不同频率的三角函数，有效区分长短程，Long Context的关键一环。
• 形式简单，RoPE直接作用于Q、K，不改变Attention的形式
  • 与当前Attention机制结合更契合，比如Flash Attention，更容易Scale Up。

RoPE缺点

长度外推性较弱

• 推理长度超过训练长度时，性能急剧下降，表现为困惑度急剧上升。
• 解释：
  • 训练长度L，位置0到L-1，旋转弧度范围 $[0,(L-1){\theta }_i]$
  • 推理长度大于L，旋转弧度大于 $(L-1){\theta }_i$，模型难以理解新的旋转弧度
  • 无法正确注入位置信息，导致性能下降。

推理长度超过训练长度，性能下降、困惑度增高。

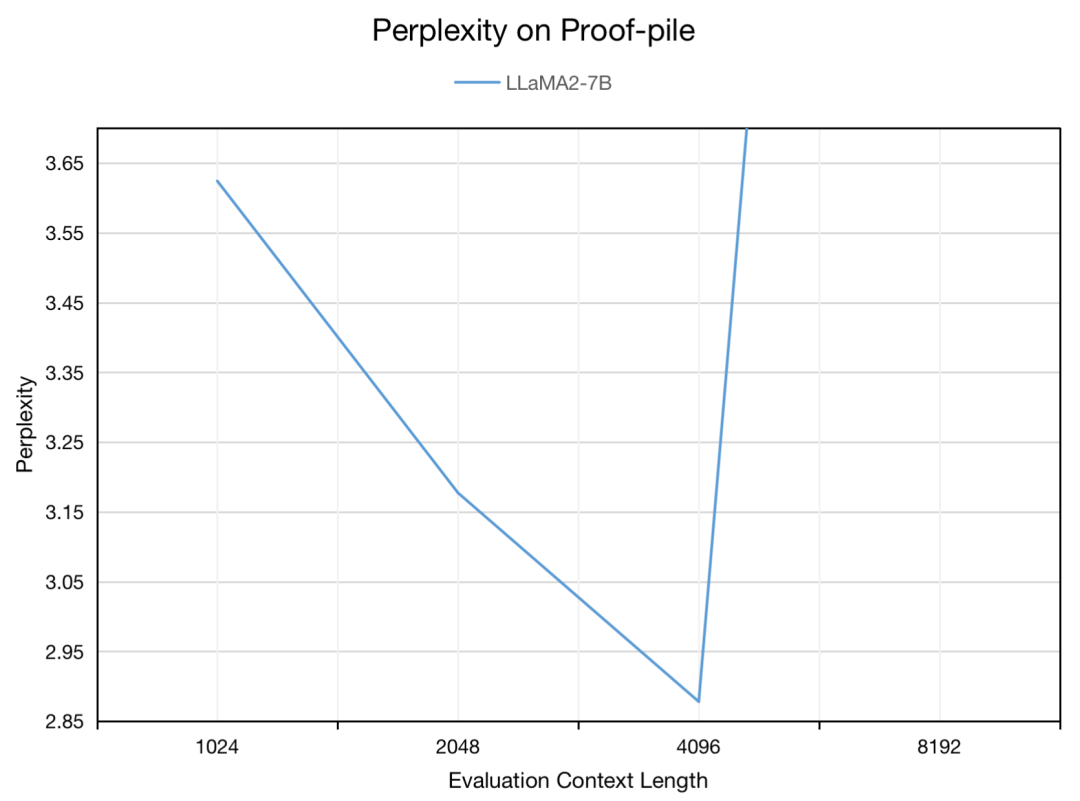
训练[0,2047]，推理时未见[2048,4095]。

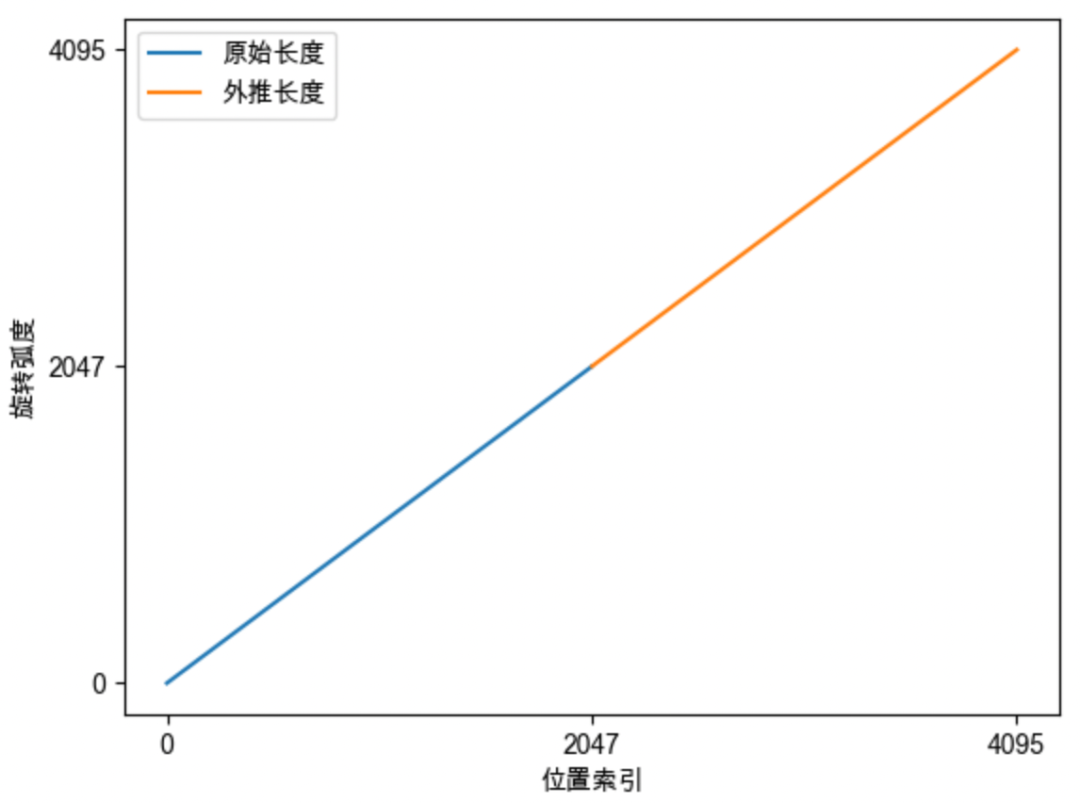
基于RoPE的长度外推

参考文章

• 详解基于调整RoPE旋转角度的大模型长度外推方法
• 上下文长度扩展：从RoPE到YARN

RoPE 长度外推总结

RoPE长度外推总结

0. 背景

• RoPE超过训练长度L，性能会下降。

• 当向量q位于位置m时，只需把第i组分量，旋转$m{\theta }_i$弧度，即得具有绝对位置信息的$q_m$

  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}=m\cdot \frac{1}{{\text{base}}^{2i/d}}$$$$q_m=f(q,m)=R_m\cdot q$$

• 放大base，缩小每个位置的旋转弧度$m{\theta }_i$，来提升模型输入长度。

  • 但base太大，会使注意力远程衰减的性质变弱，改变意力分布，导致模型输出质量下降

1. 线性位置插值

• 模型已能理解$[0,(L-1){\theta }_i]$，使用该弧度旋转范围表示更长的长度范围$[0,L^{\prime }-1]$

• 长度 扩大几倍，旋转弧度 缩小几倍

  $$m{\theta }_i\cdot \frac{L}{L^{\prime }}=m{\text{base}}^{-2i/d}\cdot \frac{L}{L^{\prime }}$$

2. NTK-Aware 插值

• 应该保留高频信息，高频做外推，低频做内插。不同分组应该有区分度。
• 对base进行放大(如100倍)。高频分量 降幅低，做外推；低频分量 降幅高，做内插。

$$m{\theta }_i=m\cdot (\text{base}\cdot \alpha {)}^{-2i/d}$$

3. NTK-by-parts

• NTK-Aware存在过度外推情况，定义旋转周期(波长)，周期个数(序列和波长比值)。

  $${\lambda }_i=\frac{2\pi }{{\theta }_i}=2\pi \cdot {\text{base}}^{2i/d}$$$$r(i)=\frac{L}{{\lambda }_i}$$

• 定义高低频边界，高频做外推，低频做内插。

  $$\text{外推程度}\gamma (i)=\{\begin{array}{ll}1,& r(i)\ge \beta \\ \frac{r(i)-\alpha }{\beta -\alpha }& \alpha <r(i)<\beta \\ 0,& r(i)\le \alpha =1\end{array}$$

4. Dynamic NTK

• 超出训练长度 时$l>L$才做插值，每一步通过NTK-Aware，动态放大base$$m{\theta }_i=m\cdot (\text{base}\cdot \alpha {)}^{-2i/d},\alpha =(\frac{l}{L}{)}^{d/(d-2)}$$

5. YaRN (NTK-by-parts + Attention Scaling)

• 对低频做线性插值，对高频做外推，同NTK-by-parts

• 同时修正注意力分布，除以温度t

  $$\frac{{\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_n}{\sqrt{d}}\to \frac{{\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_n}{t\sqrt{d}}$$$$\sqrt{\frac{1}{t}}=0.1\cdot \ln (\frac{L^{\prime }}{L})+1(\mathrm{注}\mathrm{意}：1\text{为mscale系数})$$

内插和外推

内插和外推

外推

• 保持相邻点的间隔为1不变，直接扩展取值范围，比如 [0, 4) -> [0, 8)

内插

• 维持原先的区间不变，从原区间取更多的点来表示新的位置
  • 比如，维持取值范围[0,4)，但相邻点间隔 从1缩小至0.5

线性位置插值

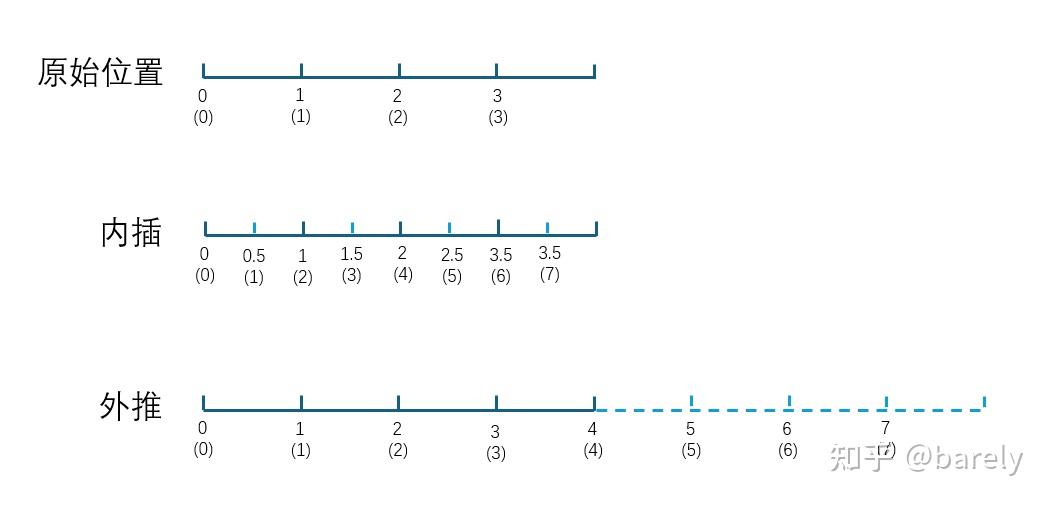
线性位置插值

背景

• RoPE训练长度L，旋转弧度范围 $[0,(L-1){\theta }_i]$

核心思想

• 模型已能理解$[0,(L-1){\theta }_i]$，使用该弧度旋转范围表示更长的长度范围$[0,L^{\prime }-1]$

具体做法

• 缩小每个位置的旋转弧度，让向量旋转的慢一些

  • 每个位置旋转弧度变成原来的$\frac{L}{L^{\prime }}$。

  • 长度扩大几倍，旋转弧度缩小几倍。

    $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}\to m{\theta }_i\cdot \frac{L}{L^{\prime }}=m{\text{base}}^{-2i/d}\cdot \frac{L}{L^{\prime }}$$

• 在原来的弧度范围内，插入更多位置，由于线性变化，也称做线性插值。

缺点(根据下文NTK理论)

• 输入特征高频分量对模型很重要。
• 但线性插值，对高低频，所有分组 不加区分缩小弧度
• 导致高频分量的分布发生变化，导致高频信息缺失，影响模型性能。

扩展后，原[0,2048]弧度范围，可表示长度[0,4096]。线性位置插值。

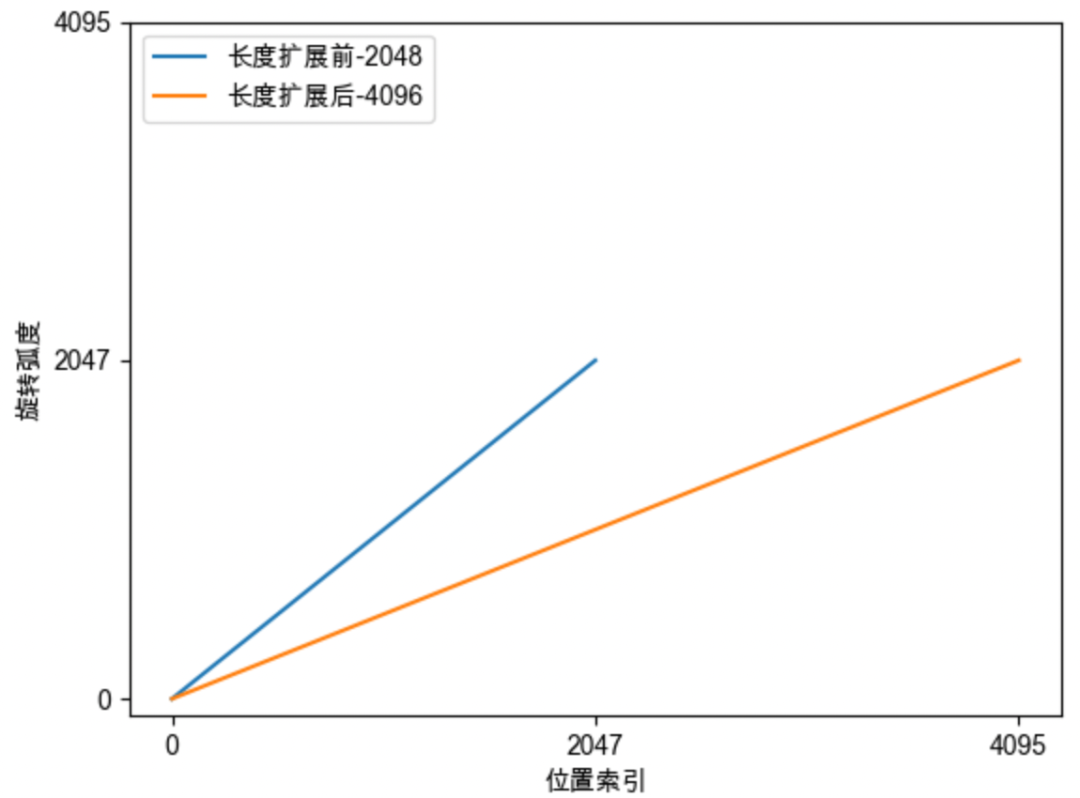
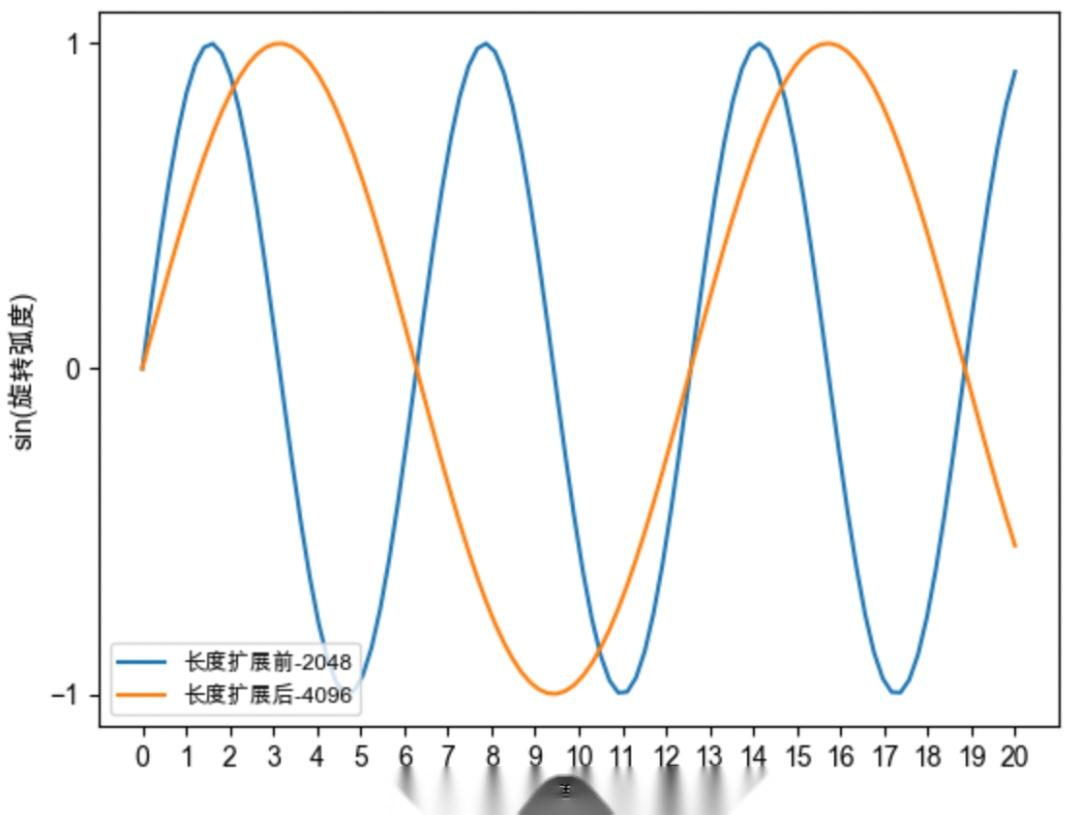
位置插值后，旋转速度变慢，周期变大、频率变慢。

NTK-Aware 插值

NTK-Aware 插值

背景

• 高频信息对NN非常重要。RoPE中，分组越靠前，旋转速度越快，越靠后，越慢。
• 但线性插值，对所有分组 不加区分缩小弧度，会导致高频信息缺失，影响性能。
• NTK-Aware 希望保留高频信息 (靠前的向量分组)。
• 模型对高频分量敏感，应该高频外推，低频内插。

核心公式

• 新增$\alpha$参数，在所有位置位置，对base进行缩放。如放大100倍。

  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}\to m{\theta }_i=m\cdot (\text{base}\cdot \alpha {)}^{-2i/d}\to m\cdot (10000\cdot \alpha {)}^{-2i/d}$$
  • 调整后弧度和调整前弧度的倍数比。

$$\frac{m\cdot (\text{base}\cdot \alpha {)}^{-2i/d}}{m\cdot (\text{base}{)}^{-2i/d}}={\alpha }^{-2i/d}=\frac{1}{{\alpha }^{2i/d}}$$

• 把外推程度定义成和组别i有关的函数$\gamma (i)$

  $$f(m,i)=g(m)\cdot \gamma (i)\cdot h({\theta }_i)$$$$\gamma (i)=\{\begin{array}{ll}1,& i=0\\ (\frac{L^{\prime }}{L}{)}^{\frac{-2d}{d-2}},& 0<i<\frac{d}{2}-1\\ 0,& i=\frac{d}{2}-1\end{array}$$

NTK-Aware 保留高频信息：高频外推，低频内插

• 靠前的分组

  • 高频分量， 旋转速度降幅低。在高频部分进行外推。

  • 见过较多的完整旋转周期，得到充分训练，具有较强外推能力。

• 靠后的分组

  • 低频分量，旋转速度降幅高。低频部分进行内插。
  • 见到的旋转周期少，训练不充分，外推性能弱，需要进行位置插值。

结果

• Code LLaMA base=10000：$\alpha =100$，把base放大100倍。
• 不进行finetune时，NTK-Aware插值效果比线性插值更优。

缺点

• 存在过度外推情况。

  • 比如一些低频分量，即使训练最长序列，也没办法经过完整周期。

  • 对于这些分量，不应该进行任何外推，可能引入未见过的旋转角度。

    $${\lambda }_i$$

调整后旋转倍数关系：前面的分量、旋转转速快、降幅小，后面的分量、旋转速度慢、降幅大。

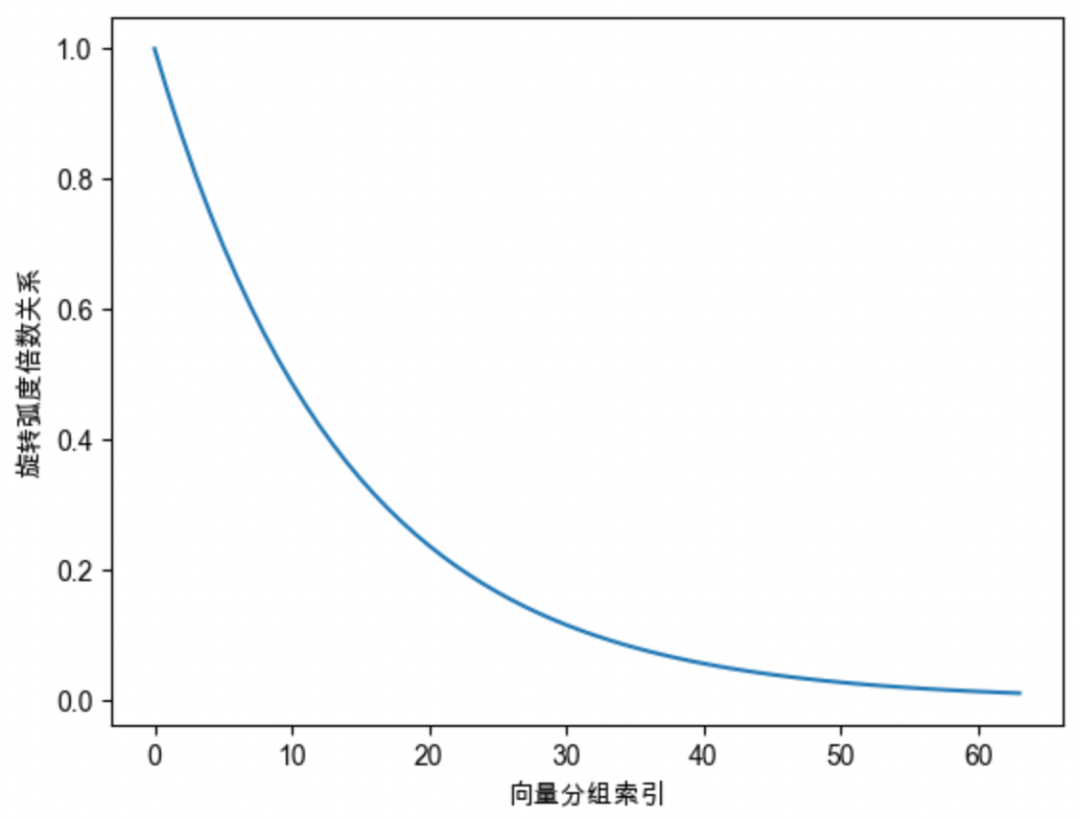
第0组，在位置7，已经旋转一周；第64组，在位置2047时，旋转弧度为0.2047，仍未完成1/4旋转。

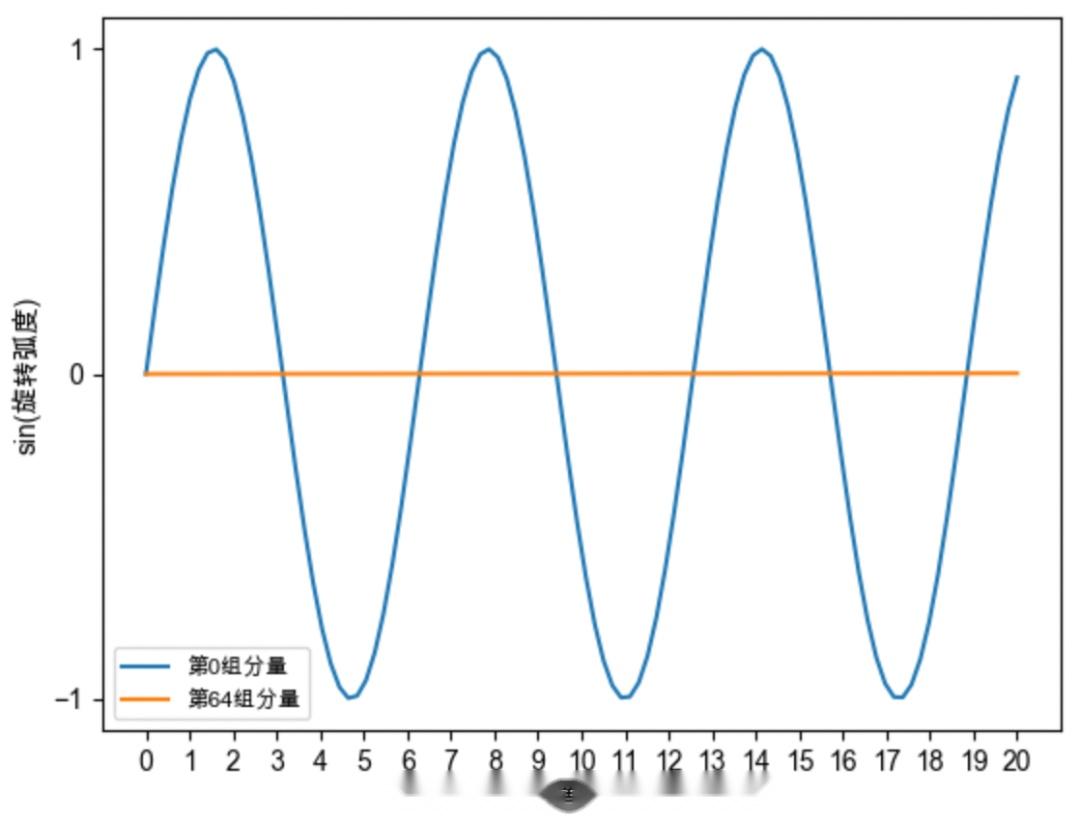
拟合曲线

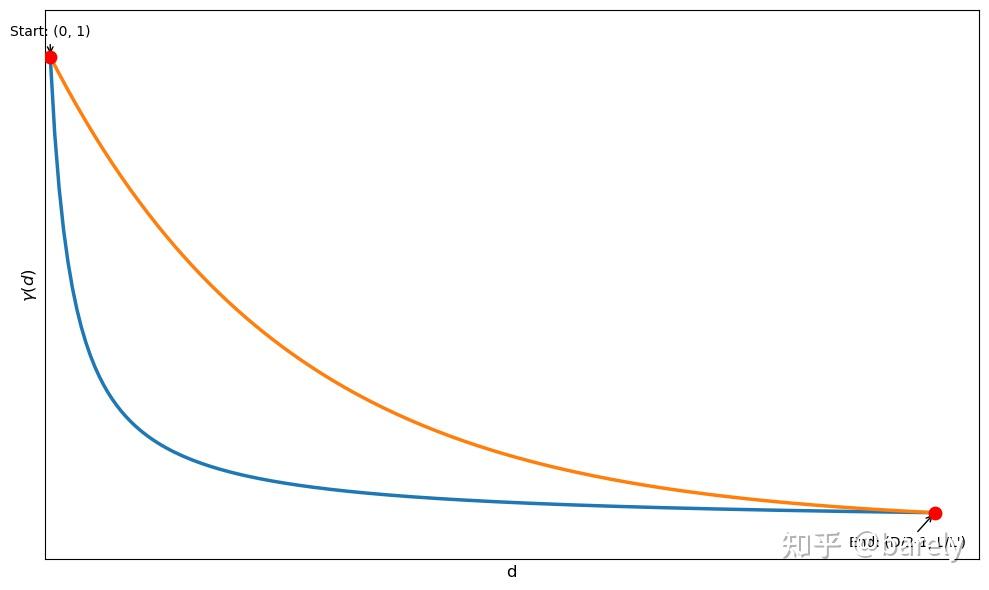
NTK-by-parts 插值

NTK-by-parts Interpolation

NTK-Aware缺点

• 存在过度外推情况。

  • 比如一些低频分量，即使训练最长序列，也没办法经过完整周期。

  • 对于这些分量，不应该进行任何外推，可能引入未见过的旋转角度。

    $${\lambda }_i=2\pi b^{2i/d}\ge L\to i\ge \frac{d}{2}{\log }_{\text{base}}(\frac{L}{2\pi })$$

核心思想

• 不改变 高频部分，仅缩小 低频部分的旋转弧度。
  • 对高频分量：做完全外推；
  • 对低频分量：做内插。
  • 对中间部分分量：既做外推、又做内插。

两个概念定义

• 第i个分组的旋转周期 、波长，${\lambda }_i$

  $${\lambda }_i=\frac{2\pi }{{\theta }_i}=2\pi \cdot {\text{base}}^{2i/d}$$

• 序列长度和波长的比值， $r(i)$，第i个分组在训练长度内的周期个数 。

$$r(i)=\frac{L}{{\lambda }_i}$$

高低频区分

• 如果周期个数较多，$r(i)>\beta$，高频部分，则做完全外推，无需改变。

• 如果周期个数较少，$r(i)<\alpha =1$，低频部分，则只做内插。

• 如果介于中间，$\alpha \le r(i)<\beta$，既做外推，又做内插。

  • 外推程度
  $$\text{外推程度}\gamma (i)=\{\begin{array}{ll}1,& r(i)\ge \beta \\ \frac{r(i)-\alpha }{\beta -\alpha }& \alpha <r(i)<\beta \\ 0,& r(i)\le \alpha =1\end{array}$$

• 命名

  • $\alpha ={\beta }_{\text{slow}}=1$，$\beta ={\beta }_{\text{fast}}=32$

Dynamic NDK 插值

笔记

背景

• 前面的方法优缺点
  • 超出训练长度时：插值比直接外推效果好
  • 在训练长度内时：推理表现比原模型差

核心思想

• 推理长度小于训练长度时 $l\le L$：不插值

• 推理长度大于训练长度时 $l>L$：

  • 每一步通过NTK-Aware 插值，动态放大base，l逐步+1。
  $$m{\theta }_i=m\cdot (\text{base}\cdot \alpha {)}^{-2i/d}$$$$\alpha =(\frac{l}{L}{)}^{d/(d-2)}$$

YaRN

背景

YaRN 背景

背景

• 线性插值+NTK方法核心：通过减小旋转弧度，来扩展长度。

• 插值缺点

  • 词向量距离变得更近、内积变大，破坏了 模型原始的注意力分布。
  • 表现
    • 模型在训练内长度困惑度提升，性能受损
    • RoPE的注意力远程衰减性质变弱，使得整个注意力分布变大更平滑

• 内积为何变大

  • 向量旋转不改变模长，q和k的旋转弧度变小，导致夹角$\gamma$变小，因此内积会变大
  $$q\cdot k=|q|\cdot |k|\cdot \cos (\gamma )$$

核心思想

YaRN 核心思想

核心思想

• NTK-by-parts + Attention-scaling

  • 对低频做线性插值，对高频做外推，同时修正注意力分布，除以温度t

• 仅缩小低频部分的旋转弧度，且通过温度系数t 修正注意力分布

  • 将原来的注意力分数，除以温度t 即可
  $$\frac{{\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_n}{\sqrt{d}}\to \frac{{\mathit{q}}_m^{\mathrm{\top }}{\mathit{k}}_n}{t\sqrt{d}}$$
  • 温度系数t由$L\mathrm{和}{L}^{\prime }$一起计算得来$$\sqrt{\frac{1}{t}}=0.1\cdot \ln (\frac{L^{\prime }}{L})+1(\mathrm{注}\mathrm{意}：1\text{为mscale系数})$$

示例

• $L=2048,L^{\prime }=16384$，计算得t=0.6853
  • t变大：注意力分布平滑，方差更小
  • t变小：注意力分布更尖锐，区分度更大，方差变大
  • t=0.6853，缓解注意力分布过于平滑的问题，让注意力分布方差更大

DeepSeek R1 Yarn 配置

Yarn 配置

关键配置

• 基础RoPE旋转弧度：rope_theta, self.base, 10000 。计算每个分量的旋转角频率。

  $$m{\theta }_i=m\cdot {\text{base}}^{-2i/d}$$

• NTK-by-parts 外推

  • 外推总长度，L=original_max_position_embeddings

    $$L^{\prime }=L\ast \text{factor},4096\ast 40=163840$$

  • 旋转周期、波长

    $${\lambda }_i=\frac{2\pi }{{\theta }_i}=2\pi \cdot {\text{base}}^{2i/d}$$

  • 周期个数

    $$r(i)=\frac{L}{{\lambda }_i}$$

  • 低频边界：$\alpha ={\beta }_{\text{slow}}=1$，高频边界：$\beta ={\beta }_{\text{fast}}=32$

  $$\text{外推程度}\gamma (i)=\{\begin{array}{ll}1,& r(i)\ge \beta \\ \frac{r(i)-\alpha }{\beta -\alpha }& \alpha <r(i)<\beta \\ 0,& r(i)\le \alpha =1\end{array}$$

  • 对低频做线性插值。

    $$m{\theta }_i\cdot \frac{L}{L^{\prime }}=m{\text{base}}^{-2i/d}\cdot \frac{L}{L^{\prime }}$$

  • 对高频做外推。

• 温度系数：修正注意力

  • 根据新旧长度长度计算温度系数
  $$\sqrt{\frac{1}{t}}=0.1\cdot \ln (\frac{L^{\prime }}{L})+1(\mathrm{注}\mathrm{意}：1\text{为mscale系数})$$

DeepSeek-R1 配置文件

rope_scaling": {
    "beta_fast": 32,
    "beta_slow": 1,
    "factor": 40,
    "mscale": 1.0,
    "mscale_all_dim": 1.0,
    "original_max_position_embeddings": 4096,
    "type": "yarn"
  },
"rope_theta": 10000,

DeepSeek-R1 模型代码

# 1. 定义两种频率计算方式

# freq_extra: 对应“外推”，即原始的、不缩放的频率
# 对应理论中的高频部分，我们希望保留它的旋转速度
freq_extra = 1.0 / (
    self.base ** (torch.arange(0, dim, 2, dtype=torch.float32, device=device) / dim)
)

# freq_inter: 对应“内插”，即使用 scaling_factor 缩放后的频率
# self.scaling_factor 就是 config 里的 "factor"
# 对应理论中的低频部分，我们希望让它转得更慢
freq_inter = 1.0 / (
    self.scaling_factor
    * self.base
    ** (torch.arange(0, dim, 2, dtype=torch.float32, device=device) / dim)
)

# 2. 确定高频、低频、中间部分的“分界线”

# low, high 是维度索引 (dimension index)
# 它根据 beta_fast 和 beta_slow 计算出哪些维度属于“高频”，哪些属于“低频”
# 这个计算过程比较tricky，但其目的就是找到一个维度区间，用于做平滑过渡
low, high = yarn_find_correction_range(
    self.beta_fast,       # config["beta_fast"] = 32
    self.beta_slow,       # config["beta_slow"] = 1
    dim,
    self.base,
    self.original_max_position_embeddings, # config["original_max_position_embeddings"] = 4096
)

# 3. 创建一个“混合蒙版”(blending mask)

# yarn_linear_ramp_mask 会创建一个从 0 到 1 的平滑斜坡
# inv_freq_mask 的结果是：
# - 在“高频”维度上，值接近 1
# - 在“低频”维度上，值接近 0
# - 在“中间”维度上，值从 1 平滑过渡到 0
inv_freq_mask = 1.0 - yarn_linear_ramp_mask(low, high, dim // 2).to(
    device=device, dtype=torch.float32
)

# 4. 混合高频和低频的频率

# 这行代码是 NTK-by-parts 的精髓！
# 当 inv_freq_mask[i] 接近 1 时 (高频)，inv_freq[i] ≈ freq_extra[i] (外推)
# 当 inv_freq_mask[i] 接近 0 时 (低频)，inv_freq[i] ≈ freq_inter[i] (内插)
# 中间部分则是两种频率的线性组合，实现了平滑过渡
inv_freq = freq_inter * (1 - inv_freq_mask) + freq_extra * inv_freq_mask

self.register_buffer("inv_freq", inv_freq, persistent=False)

# 后面就是用这个最终的 inv_freq 来计算 cos 和 sin cache
t = torch.arange(seq_len, device=device, dtype=torch.float32)
freqs = torch.outer(t, inv_freq)
...

# 5. 计算 Attention Scaling 因子
# self.mscale 就是 config 里的 "mscale"
# self.scaling_factor 就是 config 里的 "factor"
_mscale = float(
    yarn_get_mscale(self.scaling_factor, self.mscale) 
    / yarn_get_mscale(self.scaling_factor, self.mscale_all_dim) # mscale_all_dim 通常是 1.0
)


# 6. 将缩放因子应用到 cos 和 sin 缓存上
emb = torch.cat((freqs, freqs), dim=-1)
# 在生成 cos 和 sin 缓存时，直接乘上 _mscale
self.register_buffer(
    "cos_cached", (emb.cos() * _mscale).to(dtype), persistent=False
)
self.register_buffer(
    "sin_cached", (emb.sin() * _mscale).to(dtype), persistent=False
)