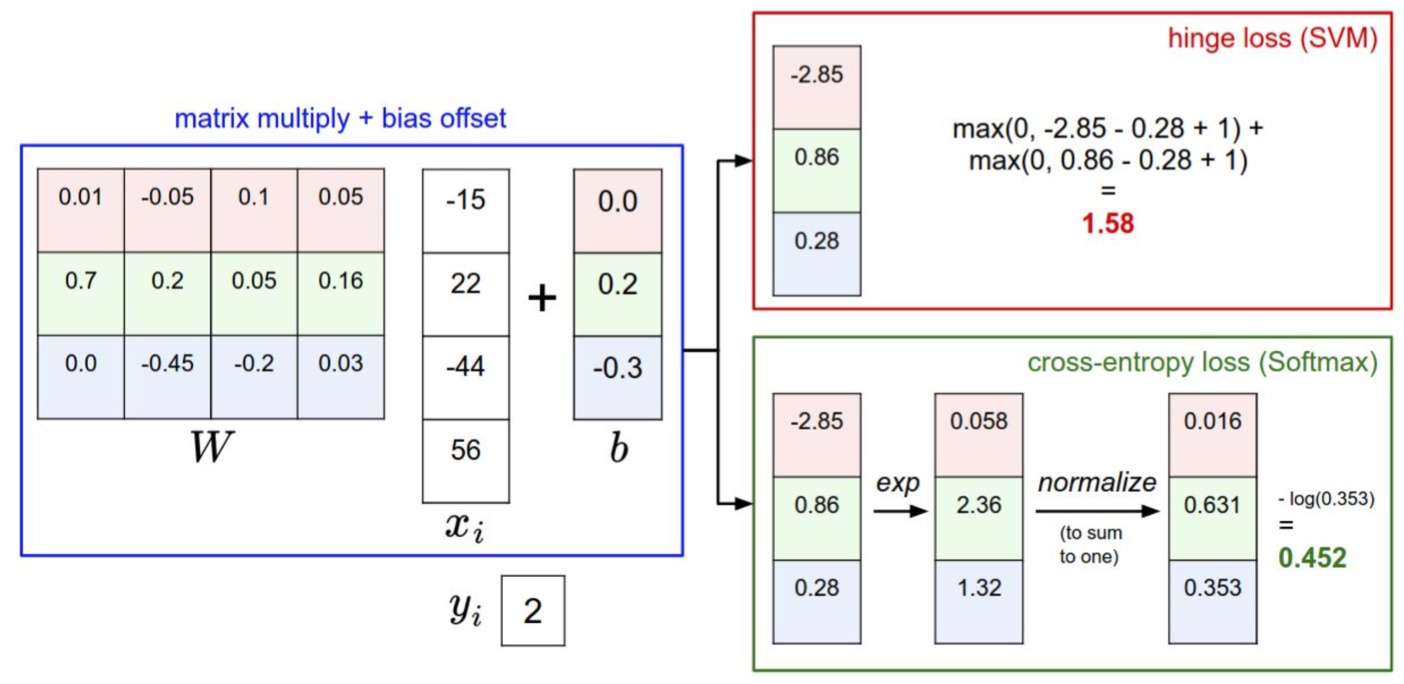
线性分类器，svm和交叉熵损失函数

线性分类器

得分函数

图片是三维数组，元素在0-255的整数。宽度-高度-3 ，3代表RGB颜色通道。 对图像进行零中心化。

输入图片$D=32\times 32\times 3=3072$个像素，压缩成1维向量，一共有$K=10$个类别。

$$f(x_i,W,b)=W{x}_i+b$$

分析

• $W$的每一行都是一个类别的分类器，一共10个
• 得到分为每个类的score
• 改变$W,b$ ，使得分类准确，正确的score高，错误的score低

为x添加一维，$x\in {\mathbb{R}}^{D+1}$ ， 写为：

$$f(x_i,W)=W{x}_i$$

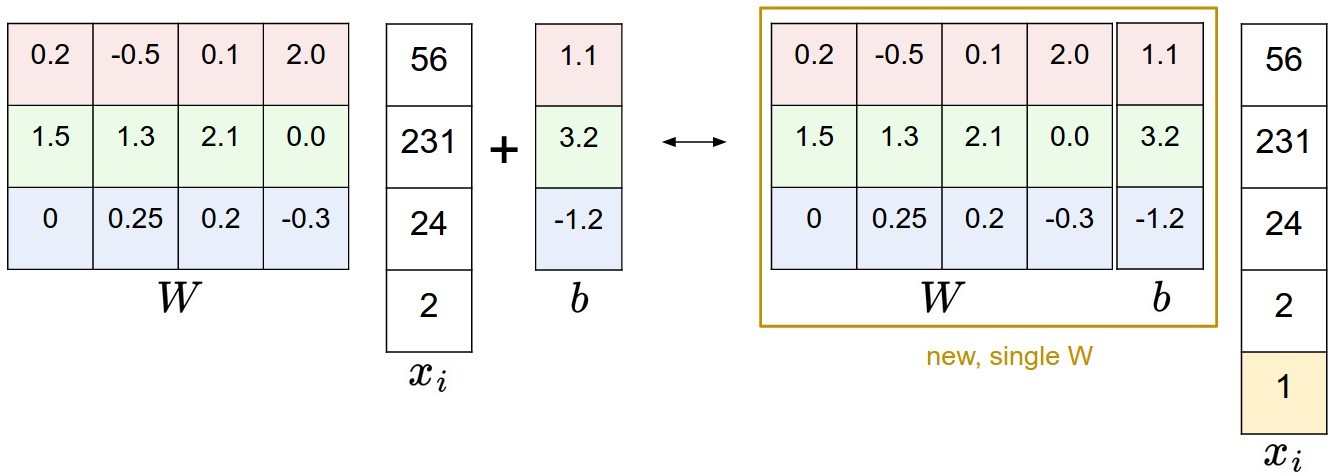
理解

权重

输入4个像素，函数会根据权重对某些位置的某些颜色表现出喜好或者厌恶（正负）。

比如船类别，一般周围有很多蓝色的水，那么蓝色通道的权值就会很大（正）。绿色和红色就比较低（负）。那么如果出现绿色和红色的像素，就会降低是船的概率。

权重解释2

$W$的每一行对应于一个分类的模板(原型)， 用图像和模板去比较，计算得分（点积），找到最相似的模板。

线性函数

实际上，每个输入$x_i$就是3072维空间中的一个点，线性函数就是对这些点进行边界决策分类。 与线的距离越大，得分越高。

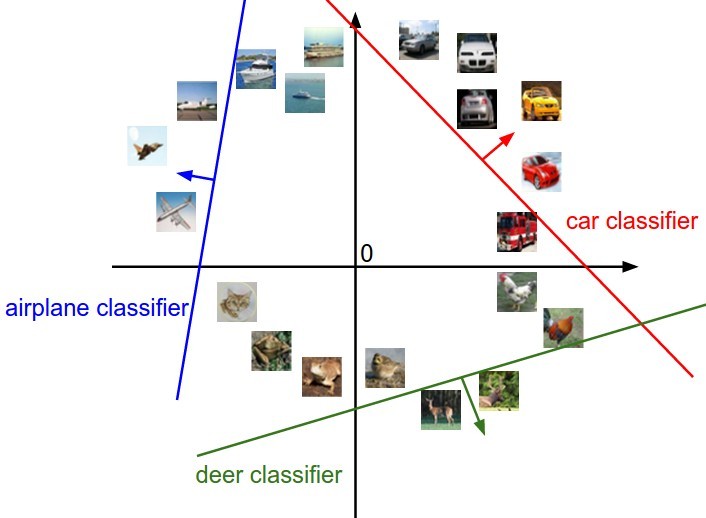
损失函数

最常用两个分类器：SVM和Softmax。分别使用SVM loss和交叉熵loss。

SVM

多类支持向量积损失（Multiclass Support Vector Machine）。正确分类比错误分类的得分高出一个边界值$\mathrm{\Delta }(\mathrm{一}\mathrm{般}=1)$ 。

记$x_i$分为第j个类别的得分为$s_j=f(x_i,W{)}_j$ ，单个折叶损失 hinge loss， 也称作max margin loss ，如下：

$$\begin{array}{rl}loss& =max(0,s_j-s_{y_i}+\mathrm{\Delta })=\{\begin{array}{lll}& 0,& s_{y_i}-s_j>\mathrm{\Delta }\\ & s_j-s_{y_i}+\mathrm{\Delta },& \mathrm{其}\mathrm{它}\end{array}\\ \\ & =max(0,w_j^T{x}_i-w_{y_i}^T{x}_i+\mathrm{\Delta })\end{array}$$

如果错误分类进入红色区域，就开始计算loss。

第$i$个数据的loss就是把所有错误类别的loss加起来：

$$L_i=\sum _{j\ne y_i}max(0,s_j-s_{y_i}+\mathrm{\Delta })$$

正则化

plmsmile的L2正则化

使用L2正则化，对$W$的元素进行平方惩罚， 抑制大数值的权值。正则化loss（正则化惩罚）如下：

$$R(W)=\sum _k\sum _l{W}_{kl}^2$$

最终loss就是数据损失+正则化损失， $\lambda$ 是正则化强度。

$$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i{L}_i}}+\underset{\text{正则化 loss}}{\underbrace{\lambda R(W)}}$$

引入正则化以后，SVM就有了最大边界max margin 这一个良好性质。（不是很懂，后面再解决）

Softmax

plmsmile的交叉熵

每个类别的得分

$$s_j=f(x_i,W{)}_j=f_j$$

Softmax函数求得$x_i$分为第$j$ 类的概率，这样会求得所有类别的概率，即预测的结果。

$$p(j\mid x_i)=\frac{\exp (f_j)}{\sum _k\exp (f_k)}$$

单个数据的loss，就是取**其概率的负对数 ** ：

$$L_i=-\log p(y_i\mid x_i)=-\log \left(\frac{e^{f_{y_i}}}{\sum e^{f_k}}\right)=-f_{y_i}+\log \sum _k{e}^{f_k}$$

从直观上看，最小化loss就是要最大化正确的概率（最小化正确分类的负对数概率），最小化其它分类的概率。

交叉熵的体现

程序会预测一个所有类别的概率分布$q=(p(1\mid x_i),\cdots ,p(K\mid x_i))$ 。真实label概率$p=(0,\cdots ,1,0,\cdots ,0)$ ，交叉熵：

$$\begin{array}{rl}H(p,q)& =-\sum _{x}p(x)\log q(x)\\ & =-(p(y_i)\cdot \log q(y_i))=-(1\cdot \log p(y_i\mid x_i))=-\log p(y_i\mid x_i)\end{array}$$

由于$H(p)=0$， 唯一确定，熵为0。交叉熵就等于真实和预测的分布的KL距离 。也就是说想要两个概率分布一样，即预测的所有概率密度都在正确类别上面。

$$H(p,q)=H(p)+D_{KL}(p||q)=D_{KL}(p||q)$$

结合正则化

结合正则化

$$L=\underset{\text{data loss}}{\underbrace{\frac{1}{N}\sum _i{L}_i}}+\underset{\text{正则化 loss}}{\underbrace{\lambda R(W)}}$$

最小化正确概率分类的负对数概率，就是在进行最大似然估计。正则化部分就是对W的高斯先验，这里进行的是最大后验估计。（不懂）

SVM和Softmax比较

SVM loss：希望正确分类比其他分类的得分高出一个边界值。

Softmax 交叉熵loss：希望正确分类概率大，其它分类概率小。