cs224n神经网络基础，前向反向传播，激活函数等

神经网络基础

很多数据都是非线性分割的，所以需要一种非线性non-linear决策边界 来分类。神经网络包含很多这样的非线性的决策函数。

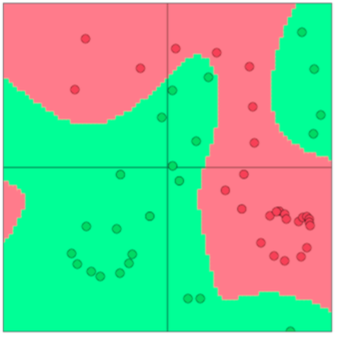
神经元

神经元其实就是一个计算单元。

• 输入向量 $x\in {\mathbb{R}}^n$
• $z=w^{T}x+b$
• $a=f(z)$ 激活函数，sigmoid, relu等，后文有讲。

Sigmoid神经元

传统用sigmoid多，但是现在一定不要使用啦。大多使用Relu作为激活函数。

$$z={\mathbf{w}}^T\mathbf{x}+b,a=\frac{1}{1+\exp (-z)}$$

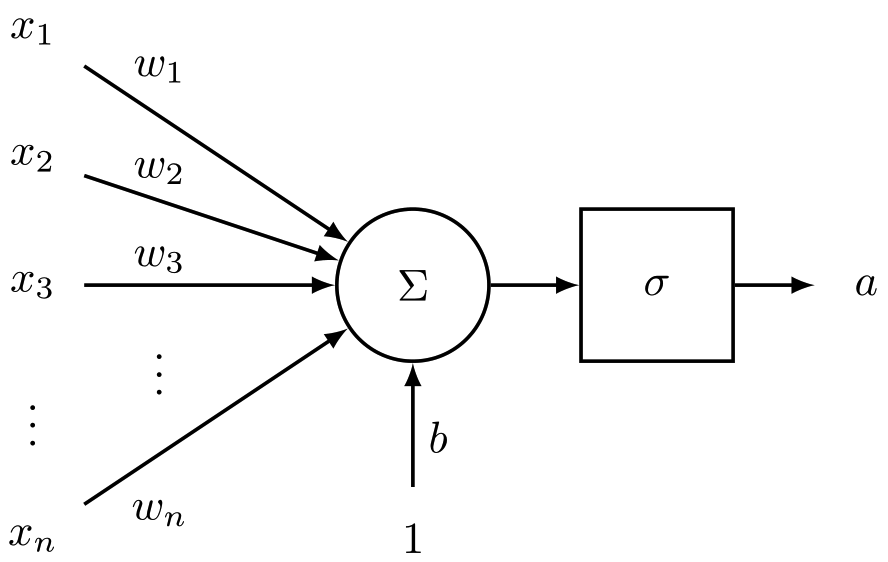
网络层

一个网络层有很多个神经元。输入$\mathbf{x}$向量，会传递到多个神经元。如

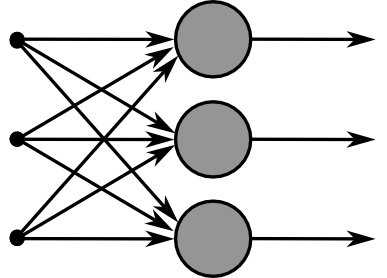
输入是$n$维，隐层是$m$维，有$m$个神经元。则有

$$\begin{array}{rlr}& z=Wx+b,& W\in {\mathbb{R}}^{m\times n},x\in {\mathbb{R}}^n,b\in {\mathbb{R}}^m\\ & a=f(z)& a\in {\mathbb{R}}^m\\ & s=U^{T}a& \mathrm{一}\mathrm{般}\mathrm{会}\mathrm{对}a\mathrm{进}\mathrm{行}\mathrm{变}\mathrm{换}\mathrm{得}\mathrm{到}\mathrm{最}\mathrm{终}\mathrm{结}\mathrm{果}s\end{array}$$

激活函数的意义

每个神经元

• 输入$z=w^{T}x+b$ ：对特征进行加权组合的结果
• 激活$a=f(z)$： 对$z$是否继续保留

最后会把所有的神经元的所有$z$的激活信息$a$综合起来，得到最终的分类结果。比如$s=U^{T}a$。

前向计算

输入$x\in {\mathbb{R}}^n$， 激活信息$a\in {\mathbb{R}}^m$。一般前向计算如下：

$$\begin{array}{rlr}& z=Wx+b,& W\in {\mathbb{R}}^{m\times n},x\in {\mathbb{R}}^n,b\in {\mathbb{R}}^m\\ \\ & a=f(z)& a\in {\mathbb{R}}^m\\ \\ & s=U^{T}a& \mathrm{一}\mathrm{般}\mathrm{会}\mathrm{对}a\mathrm{进}\mathrm{行}\mathrm{变}\mathrm{换}\mathrm{得}\mathrm{到}\mathrm{最}\mathrm{终}\mathrm{结}\mathrm{果}s\end{array}$$

下面是一个简单的全连接，最后的圆圈里的1代表等价输出。

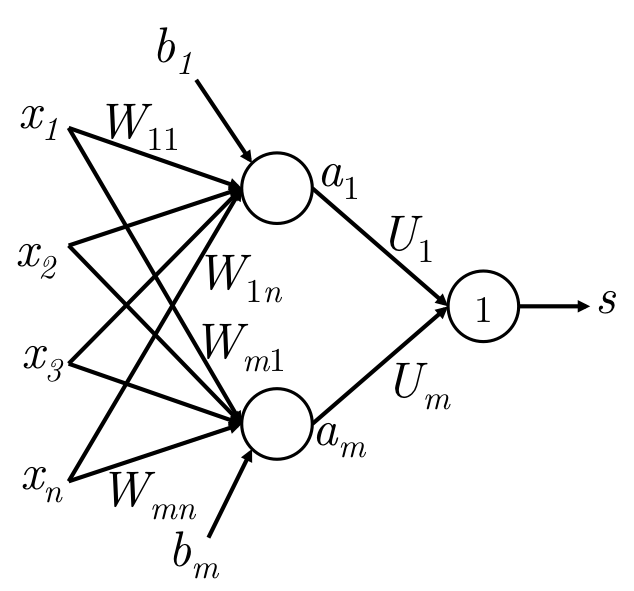
NER例子

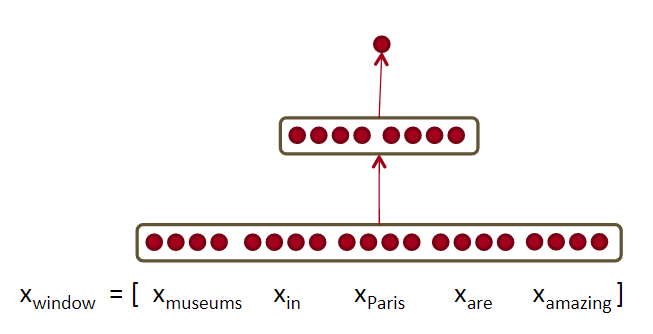
NER(named-entity recognition)，命名实体识别。对于一个句子Museums in Paris are amazing。 要判断中心单词Paris是否是个命名实体。

既要看window里的所有词向量，也要看这些词的交互关系。比如：Paris出现在in的后面。 因为可能有Paris和Paris Hilton。这就需要non-linear decisions。

如果直接把input给到softmax，是很难获取到非线性决策的。所以需要添加中间层使用神经网络。如上图所示。

维数分析

每个单词4维，输入整个窗口就是20维。在隐层使用8个神经元。计算过程如下，最终得到一个分类的得分。

$$\begin{array}{rl}& z=Wx+b\\ & a=f(z)\\ & s=U^{T}a\end{array}$$

维数如下：

$$x\in {\mathbb{R}}^{20},W\in {\mathbb{R}}^{8\times 20},U\in {\mathbb{R}}^{8\times 1},s\in R$$

Max magin目标函数

正样本$s$ ：Museums in Paris are amazing ，负样本$s_c$： Not all museums in Paris 。

只关心：正样本的得分高于负样本的得分， 其它的不关注。即要$s-s_c>0$：

$$\mathrm{maxmize}(s-s_c)\leftrightarrow \mathrm{minmize}(s_c-s)$$

优化目标函数如下：

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{J}=max({\mathrm{s}}_{\mathrm{c}}-\mathrm{s},0)=\{\begin{array}{lll}& s_c-s,& s<s_c\\ & 0,& s\ge s_c\end{array}$$

上式其实有风险，更需要$s-s_c>\mathrm{\Delta }$， 即$s$比$s_c$得分大于$\mathrm{\Delta }$，来保证一个安全的间距。

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{J}=max(\mathrm{\Delta }+{\mathrm{s}}_{\mathrm{c}}-\mathrm{s},0)$$

给具体间距$\mathrm{\Delta }=1$， 所以优化目标函数：详情见SVM。

$$\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{m}\mathrm{i}\mathrm{z}\mathrm{e}\mathrm{J}=max(1+{\mathrm{s}}_{\mathrm{c}}-\mathrm{s},0)$$

其中$s_c=U^{T}f(W{x}_c+b),s=U^{T}f(Wx+b)$ 。

反向传播训练

梯度下降 ，或者SGD：

$${\theta }^{(t+1)}={\theta }^{(t)}-\alpha \cdot {\mathrm{\Delta }}_{{\theta }^{(t)}}J$$

反向传播 使用链式法则 来计算前向计算中用到的参数的梯度。

符号定义

如下图，一个简单的网络：

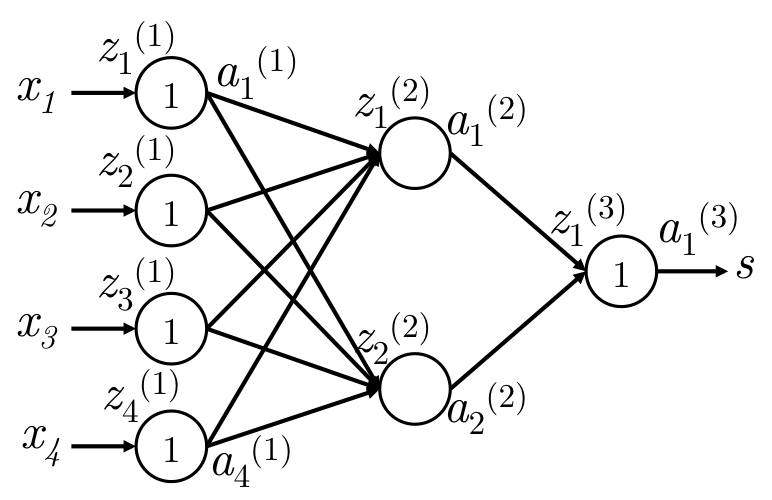
网络在输入层和输出层是等价输入和等价输出，只有中间层会使用激活函数进行非线性变换。

符号	意义
$x$	网络输入，这里是4维
$s$	网络输出，这里是1维，即一个数字
$W^{(k)}$	第$k\to k+1$层的转移矩阵。$W\in {\mathbb{R}}^{n\times m}$。 k层m个神经元，k+1层n个神经元
$W_{ij}^{(k)}$	k+1层的$i$ 神经元 到 到$k$层$j$神经元的 的权值
$b_i^{(k)}$	$k\to k+1$ 转移， k+1层的$i$ 神经元的接收偏置
$z_j^{(k)}$	第$k$层的第$j$个神经元的输入
计算输入	$z_j^{(k+1)}=\sum _i{W}_{ji}^{(k)}\cdot a_i^{(k)}+b_j^{(k)}$
$a_j^{(k)}$	第$k$层的第$j$个神经元的输入。$a=f(z)$
${\delta }_j^{(k)}$	BP时，在$z_j^{(k)}$处的梯度。即$f^{\prime }(z_j^{(k)})\cdot g$ ，$g$是传递来的梯度

W梯度推导

误差函数$J=max(1+s_c-s,0)$ ，当$J>0$的时候，$J=1+s_c-s$要去更新参数W和b。

$$\frac{\partial J}{\partial s}=-\frac{\partial J}{\partial s_c}=-1$$

反向传播时，必须知道参数在前向时所贡献所关联的对象，即知道路径。

这里是等价输出：

$$s=a_1^{(3)}=z_1^{(3)}=W_1^{(2)}{a}_1^{(2)}+W_2^{(2)}{a}_2^{(2)}$$

这里对$W_{ij}^{(1)}$的偏导进行反向传播推导：

$$\begin{array}{rl}\frac{\partial s}{\partial W_{ij}^{(1)}}& =\frac{\partial W^{(2)}{a}^{(2)}}{\partial W_{ij}^{(1)}}\\ & =\frac{\partial W_i^{(2)}{a}_i^{(2)}}{\partial W_{ij}^{(1)}}=W_i^{(2)}\cdot \frac{\partial a_i^{(2)}}{\partial W_{ij}^{(1)}}\\ & =W_i^{(2)}\cdot \frac{\partial a_i^{(2)}}{\partial z_i^{(2)}}\cdot \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}}\\ & =W_i^{(2)}\cdot f^{\prime }(z_i^{(2)})\cdot \frac{\partial }{\partial W_{ij}^{(1)}}\left(b_i^{(2)}+\sum _k^4{a}_k^{(1)}{W}_{ik}^{(1)}\right)\\ & =W_i^{(2)}{f}^{\prime }(z_i^{(2)})a_j^{(1)}\\ & ={\delta }_i^{(2)}\cdot a_j^{(1)}\end{array}$$

结果分析

我们知道$z_i^{(2)}=\sum _k^4{a}_k^{(1)}{W}_{ik}^{(1)}+b_i^{(2)}$。 单纯$z_i^{(2)}$对$W_{ij}^{(2)}$的导数是$a_j^{(1)}$。反向时，在$z_i^{(2)}$处的梯度是${\delta }_i^{(2)}$。

反向时，$\frac{\partial s}{\partial W_{ij}^{(1)}}={\delta }_i^{(2)}\cdot a_j^{(1)}$，是传来的梯度和当前梯度的乘积。这正好应证了反向传播。 传来的梯度也作error signal。 反向过程也是error sharing/distribution。

W元素实例

$W_{14}^{(1)}$ 只直接贡献于$z_1^{(2)}$和$a_1^{(2)}$

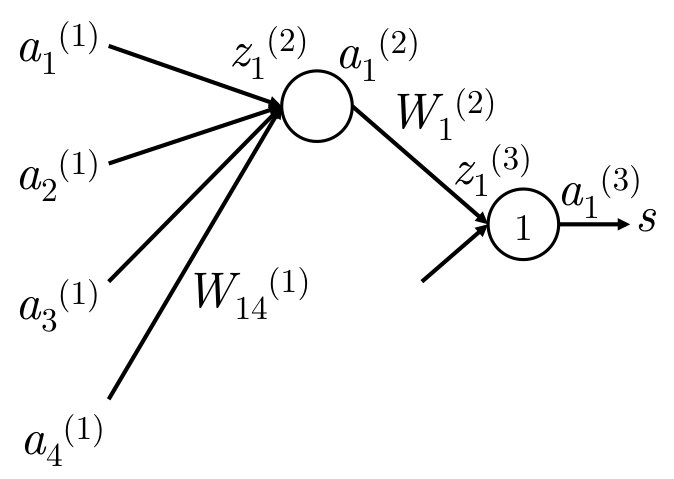
步骤	梯度
$s\to a_1^{(3)}$	梯度$g=1$。开始为1。
$a_1^{(3)}\to z_1^{(3)}$	在$z_1^{(3)}$处的梯度$g=1\cdot 1={\delta }_1^{(3)}$ 。$localg=1$ ，等价变换
$z_1^{(3)}\to a_1^{(2)}$	$g={\delta }_1^{(3)}\cdot W_1^{(2)}=W_1^{(2)}$ 。$lg=w$, $z=wa+b$
$a_1^{(2)}\to z_1^{(2)}$	$g=W_1^{(2)}\cdot f^{\prime }(z_1^{(2)})={\delta }_1^{(2)}$。 $lg=f^{\prime }(z_1^{(2)})$
$z_1^{(2)}\to W_{14}^{(1)}$	$g=W_1^{(2)}\cdot f^{\prime }(z_1^{(2)})\cdot a_4^{(1)}={\delta }_1^{(2)}\cdot a_4^{(1)}$。 $lg=a_4^{(1)}$ ， 因为$z=wa+b$
$z_1^{(2)}\to b_1^{(1)}$	$g=W_1^{(2)}\cdot f^{\prime }(z_1^{(2)})\cdot 1={\delta }_1^{(2)}\cdot a_4^{(1)}$。 $lg=1$ ， 因为$z=wa+b$

对于上式的梯度计算，有两种理解方法，通过这两种思路去思考能更深入了解。

• 链式法则
• error sharing and distributed flow approach

梯度反向传播

${\delta }_i^{(k)}\to {\delta }_j^{(k-1)}$ 传播图如下：

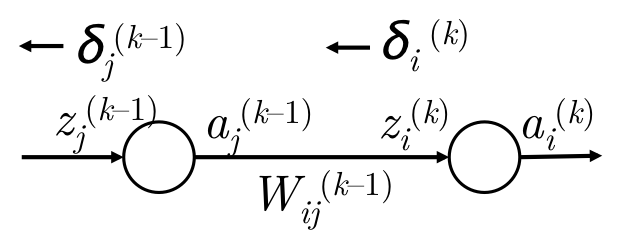
但是更多时候，当前层的某个神经元的信息会传播到下一层的多个节点上，如下图：

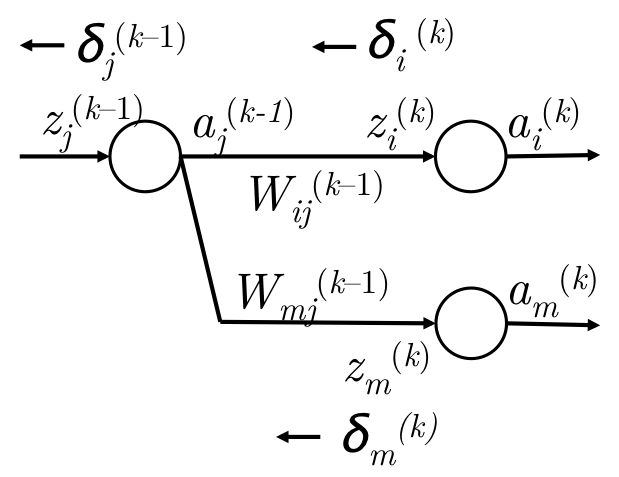
梯度推导公式如下：

$$\begin{array}{rlr}& g_w={\delta }_i^{(k)}\cdot a_j^{(k-1)}& W_{ij}^{(k-1)}\mathrm{的}\mathrm{梯}\mathrm{度}\\ \\ & g_a=\sum _i{\delta }_i^{(k)}{W}_{ij}^{(k-1)}& a_j^{(k-1)}\mathrm{的}\mathrm{梯}\mathrm{度}\\ \\ & g_z={\delta }_j^{(k-1)}=f^{\prime }(z_j^{(k-1)})\cdot \sum _i{\delta }_i^{(k)}{W}_{ij}^{(k-1)}& z_j^{(k-1)}\mathrm{的}\mathrm{梯}\mathrm{度}\\ \end{array}$$

BP向量化

很明显，不能一个一个参数地去更新element-wise。所以需要用矩阵和向量去表达，去一次性全部更新matrix-vector level。

梯度计算， $W_{ij}^{(k)}$的梯度是${\delta }_i^{(k+1)}\cdot a_j^{(k)}$ 。向量表达如下：

$${\mathrm{\Delta }}_{W^{(k)}}=\left[\begin{array}{ccc}{\delta }_1^{(k+1)}\cdot a_1^{(k)}& {\delta }_1^{(k+1)}\cdot a_2^{(k)}& \cdots \\ {\delta }_2^{(k+1)}\cdot a_1^{(k)}& {\delta }_2^{(k+1)}\cdot a_2^{(k)}& \cdots \\ ⋮& ⋮& \ddots \end{array}\right]={\delta }^{(k+1)}{a}^{(k)T}$$

梯度传播，${\delta }_j^{(k)}=f^{\prime }(z_j^{(k)})\cdot \sum _i{\delta }_i^{(k+1)}{W}_{ij}^{(k)}$。向量表达如下：

$${\delta }^{(k)}=f^{\prime }(z^{(k)})\circ ({\delta }^{(k+1)}{W}^{(k)})$$

其中$\circ$是叉积向量积element-wise，是各个位置相乘， 即${\mathbb{R}}^N\times {\mathbb{R}}^N\to {\mathbb{R}}^N$。 点积和数量积是各个位置相乘求和。

计算效率

很明显，在计算的时候要把上一层的${\delta }^{(k+1)}$存起来，去计算${\delta }^{(k)}$ ，这样可以减少大量的多余的计算。

神经网络常识

梯度检查

使用导数的定义来估计导数，去和BP算出来的梯度做对比。

$$f^{\prime }(\theta )\approx \frac{J({\theta }^{(i+)})-J({\theta }^{(i-)})}{2ϵ}$$

由于这样计算非常，效率特别低，所以只用这种办法来检查梯度。具体实现代码见原notes。

激活函数

激活函数有很多，现在主要用ReLu，不要用sigmoid。

用ReLU学习率一定不要设置太大！同一个网络中都使用同一种类型的激活函数。

Sigmoid

数学形式和导数如下：

$$\begin{array}{rl}& \sigma (z)=\frac{1}{1+\exp (-z)},\sigma (z)\in (0,1)\\ \\ & {\sigma }^{\prime }(z)=\sigma (z)(1-\sigma (z))\end{array}$$

图像

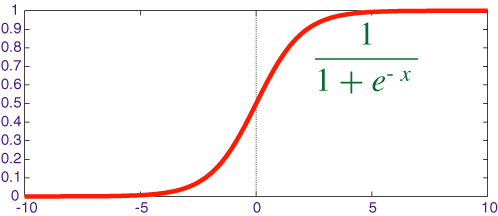
优点是具有好的解释性，将实数挤压到$(0,1)$中，很大的负数变成0，很大的正数变成1 。但现在用的已经越来越少了。有下面2个缺点。

Sigmoid会造成梯度消失

• 靠近0和1两端时，梯度会变成0。 BP链式法则，$0\times g_{from}=0$ ，后面的梯度接近0， 将没有信息去更新参数。
• 初始化权重过大，大部分神经元会饱和，无法更新参数。因为输入值很大，靠近1了。$f^{\prime }(z)=0$， 没法传播了。

Sigmoid输出不是以0为均值

• 如果输出$x$全是正的，$z=wx+b$， 那么$\frac{\partial z}{\partial w}=x$ 梯度就全是正的
• 不过一般是batch训练，其实问题也还好

Sigmoid梯度消失的问题最严重。

Tanh

数学公式和导数如下：

$$\begin{array}{rl}& \tanh (z)=\frac{\exp (z)-\exp (-z)}{\exp (z)+\exp (-z)}=2\sigma (2z)-1,\tanh (z)\in (-1,1)\\ \\ & {\tanh }^{\prime }(z)=1-{\tanh }^2(z)\end{array}$$

图像：

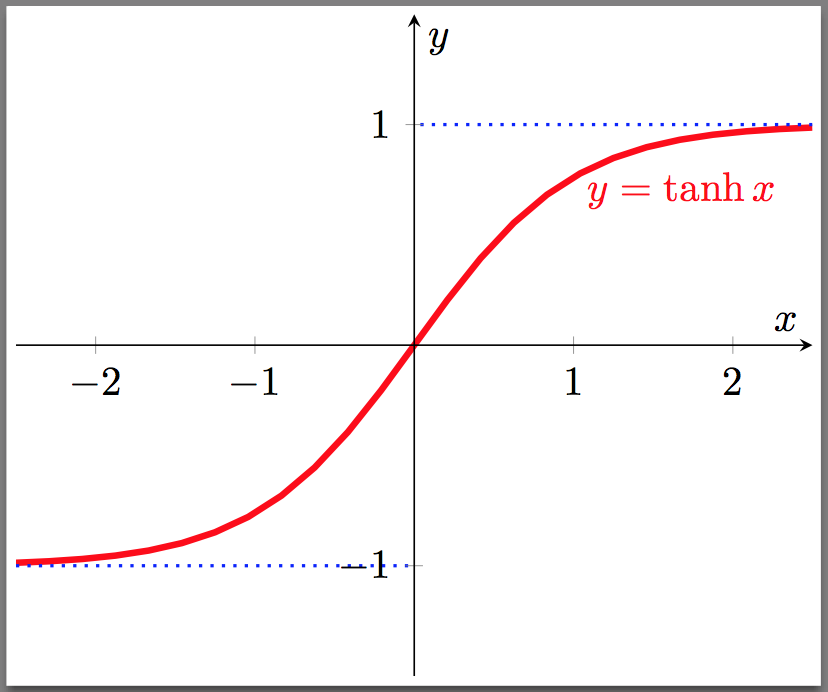
Tanh是Sigmoid的代替，它是0均值的，但是依然存在梯度消失的问题。

ReLU

ReLURectified Linear Unit 最近越来越流行，不会对于大值$z$就导致神经元饱和的问题。在CV取得了很大的成功。

$$\begin{array}{rl}& \mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}(\mathrm{z})=max(\mathrm{z},0)\\ \\ & {\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}}^{\prime }(\mathrm{z})=\{\begin{array}{lll}& 1,& z>0\\ & 0,& z\le 0\end{array}\end{array}$$

其实ReLU是一个关于0的阈值，现在一般都用ReLU：

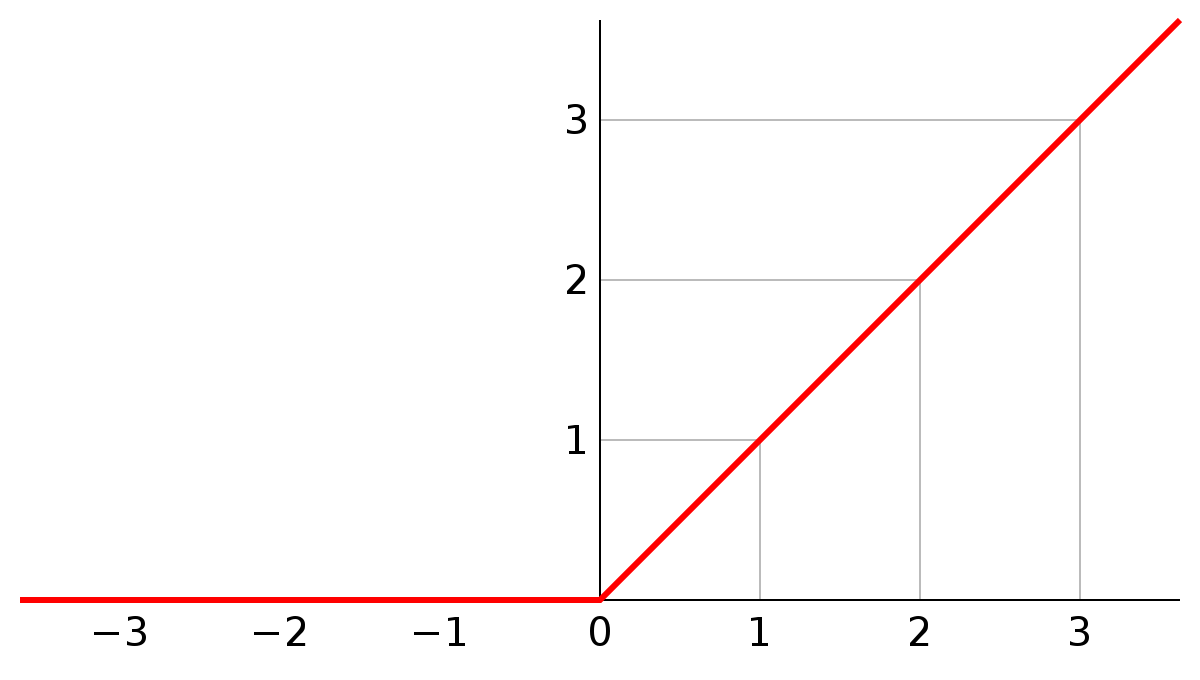
ReLU的优点

• 加速收敛（6倍）。线性的，不存在梯度消失的问题。一直是1。
• 计算简单

ReLU的缺点

训练的时候很脆弱

• BP时，如果有大梯度经过ReLU，当前在z处的梯度${\delta }^{(k+1)}=1\times g_m$ 就很大
• 对参数$w$的梯度 ${\mathrm{\Delta }}_{W^{(k)}}={\delta }^{(k)}{a}^{(k)T}$ 也就很大
• 参数$w$会更新的特别小 $W^{(k)}=W^{(k)}-\alpha \cdot {\mathrm{\Delta }}_{W^{(k)}}$
• 前向时，$z=wx+b\le 0$ 也就特别小，激活函数就不会激活
• 不激活，梯度就为0。
• 再BP的时候，就无法更新参数了

总结也就是：大梯度$\to$小参数$w$ ，新小$z = wx+b \to $ ReLU不激活， 不激活梯度为0 $\to$ 不更新参数w了。

当然可以使用比较小的学习率来解决这个问题。

Maxout

maxout 有ReLU的优点，同时避免了它的缺点。但是maxout加倍了模型的参数，导致了模型的存储变大。

$$\begin{array}{rl}& \mathrm{m}\mathrm{o}(\mathrm{x})=max({\mathrm{w}}_1\mathrm{x}+{\mathrm{b}}_1,{\mathrm{w}}_2\mathrm{x}+{\mathrm{b}}_2)\\ \\ & {\mathrm{m}\mathrm{o}}^{\prime }(\mathrm{x})=\{\begin{array}{lll}& w_1,& w_{1}x+b_1\mathrm{大}\\ & w_2,& \mathrm{其}\mathrm{它}\end{array}\end{array}$$