cs224n作业一
📅 发表于 2017/12/17
🔄 更新于 2017/12/17
👁️ -- 次访问
📝 0 字
⏳ 0 分钟
cs224n
#cs224n
#assignment
#word2vec
#cbow
#skip-gram
cs224n的第一个作业,包括softmax、神经网络基础和词向量
一般在计算softmax的时候,避免太大的数,要加一个常数。 一般是减去最大的数。
def softmax(x):
exp_func = lambda x: np.exp(x - np.max(x))
sum_func = lambda x: 1.0 / np.sum(x)
x = np.apply_along_axis(exp_func, -1, x)
denom = np.apply_along_axis(sum_func, -1, x)
denom = denom[..., np.newaxis]
x = x * denom
return x关键代码
def sigmoid(x):
s = 1.0 / (1 + np.exp(-x))
return s
def sigmoid_grad(s):
""" 对sigmoid的函数值,求梯度
"""
ds = s * (1 - s)
return ds交叉熵和softmax如下,记softmax的输入为
softmax求导
引入记号:
则有
其中两个导数
只关注有关系的部分,带入
不带入求导
所以,交叉熵的导数是
即
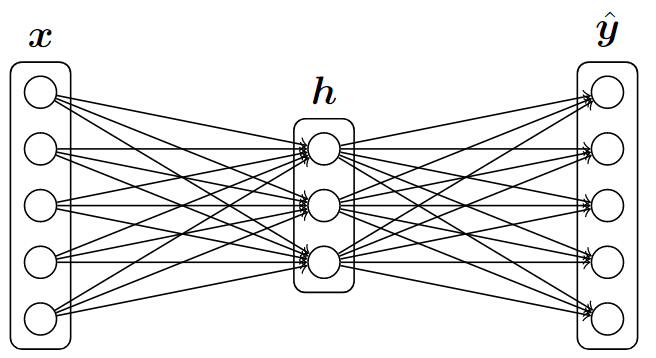
前向计算
关键代码:
def forward_backward_prop(data, labels, params, dimensions):
h = sigmoid(np.dot(data, W1) + b1)
yhat = softmax(np.dot(h, W2) + b2)loss函数
关键代码:
def forward_backward_prop(data, labels, params, dimensions):
# yhat[labels==1]实际上是boolean索引,见我的numpy_api.ipynb
cost = np.sum(-np.log(yhat[labels == 1])) / data.shape[0]反向传播
一共有
关键代码:
def forward_backward_prop(data, labels, params, dimensions):
# 前面推导的softmax梯度公式
gradyhat = (yhat - labels) / data.shape[0]
# 链式法则
gradW2 = np.dot(h.T, gradyhat)
# 本地导数是1,把第1维的所有加起来
gradb2 = np.sum(gradyhat, axis=0, keepdims=True)
gradh = np.dot(gradyhat, W2.T)
gradz1 = gradh * sigmoid_grad(h)
gradW1 = np.dot(data.T, gradz1)
gradb1 = np.sum(gradz1, axis=0, keepdims=True)
grad = np.concatenate((gradW1.flatten(), gradb1.flatten(),
gradW2.flatten(), gradb2.flatten()))
return cost, graddef gradcheck_naive(f, x):
fx, grad = f(x) # Evaluate function value at original point
h = 1e-4 # Do not change this!
# Iterate over all indexes in x
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
ix = it.multi_index
# 关键代码
x[ix] += h
random.setstate(rndstate)
new_f1 = f(x)[0]
x[ix] -= 2 * h
random.setstate(rndstate)
new_f2 = f(x)[0]
x[ix] += h
numgrad = (new_f1 - new_f2) / (2 * h)
# Compare gradients
reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
if reldiff > 1e-5:
print ("Gradient check failed.")
print ("First gradient error found at index %s" % str(ix))
print ("Your gradient: %f \t Numerical gradient: %f" % (
grad[ix], numgrad))
return
it.iternext() # Step to next dimension符号定义
前向
预测o是c的上下文概率,o为正确单词
得分向量:
loss及梯度
| 梯度 | 中文 | 计算 | 维数 |
|---|---|---|---|
| softmax | |||
| 中心词 | |||
| 上下文 |
关键代码
def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
""" Softmax cost function for word2vec models
Args:
predicted: 中心词vc
target: 上下文uo, index
outputVectors: 输出,上下文矩阵U,W*d,未转置
dataset:
Returns:
cost: 交叉熵loss
gradv: 一维向量
gradU: W*d
"""
vhat = predicted
z = np.dot(outputVectors,vhat)
preds = softmax(z)
# Calculate the cost:
cost = -np.log(preds[target])
# Gradients
gradz = preds.copy()
gradz[target] -= 1.0
gradU = np.outer(z, vhat)
gradv = np.dot(outputVectors.T, z)
### END YOUR CODE
return cost, gradv, gradU