cs224n的笔记,过拟合、预处理、初始化、Batch Normalization
过拟合
过拟合
训练数据很少,或者训练次数很多,会导致过拟合。避免过拟合的方法有如下几种:
- early stop
- 数据集扩增
- 正则化 (L1, L2权重衰减)
- Dropout
- 决策树剪枝(尽管不属于神经网络)
现在一般用L2正则化+Dropout。
过拟合时,拟合系数一般都很大。过拟合需要顾及到所有的数据点,意味着拟合函数波动很大。
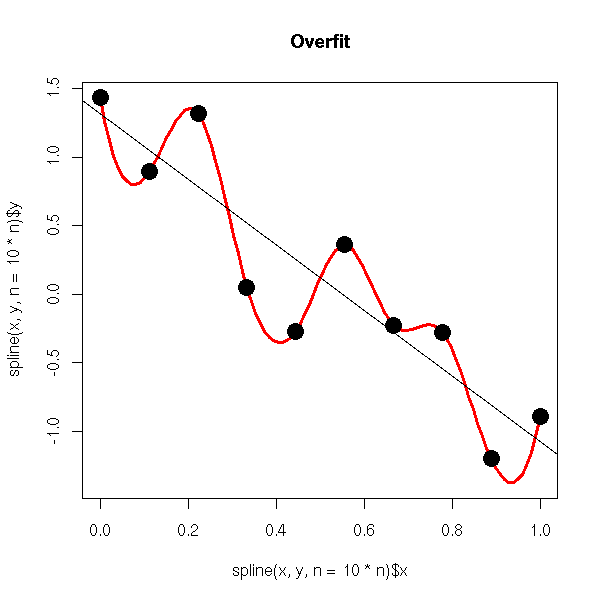
看到,在某些很小的区间内里,函数值的变化很剧烈。意味着这些小区间的导数值(绝对值)非常大。由于自变量值可大可小,所以只有系数足够大,才能保证导数值足够大。
所以:过拟合时,参数一般都很大。参数较小时,意味着模型复杂度更低,对数据的拟合刚刚好, 这也是奥卡姆剃刀法则。
范数
向量范数
| 范数 | 定义 |
|---|---|
| 1-范数 | |
| 2-范数 | |
| p-范数 | |
| - |
矩阵范数
| 范数 | 定义 |
|---|---|
| 1-范数 | |
| 2-范数 | |
| F-范数 |
L2正则化权重衰减
为了避免过拟合,使用L2正则化参数。
L2惩罚更倾向于更小更分散的权重向量,鼓励使用所有维度的特征,而不是只依赖其中的几个,这也避免了过拟合。
标准L2正则化
正则项系数,
偏导:
更新参数 :可以看出,正则化
从上式可以看出:
- 不使用正则化时,
的系数是1 - 使用正则化时
的系数是 ,效果是减小 , 所以是权重衰减 weight decay- 当然,
具体增大或减小,还取决于后面的导数项
mini-batch随机梯度下降
设
所以,权重衰减后一般可以减小过拟合。 L2正则化比L1正则化更加发散,权值也会被限制的更小。 一般使用L2正则化。
还有一种方法是最大范数限制:给范数一个上界
实例说明
增加网络的层的数量和尺寸时,网络的容量上升,多个神经元一起合作,可以表达各种复杂的函数。
如下图,2分类问题,有噪声数据。
一个隐藏层。神经元数量分别是3、6、20。很明显20过拟合了,拟合了所有的数据。正则化就是处理过拟合的非常好的办法。
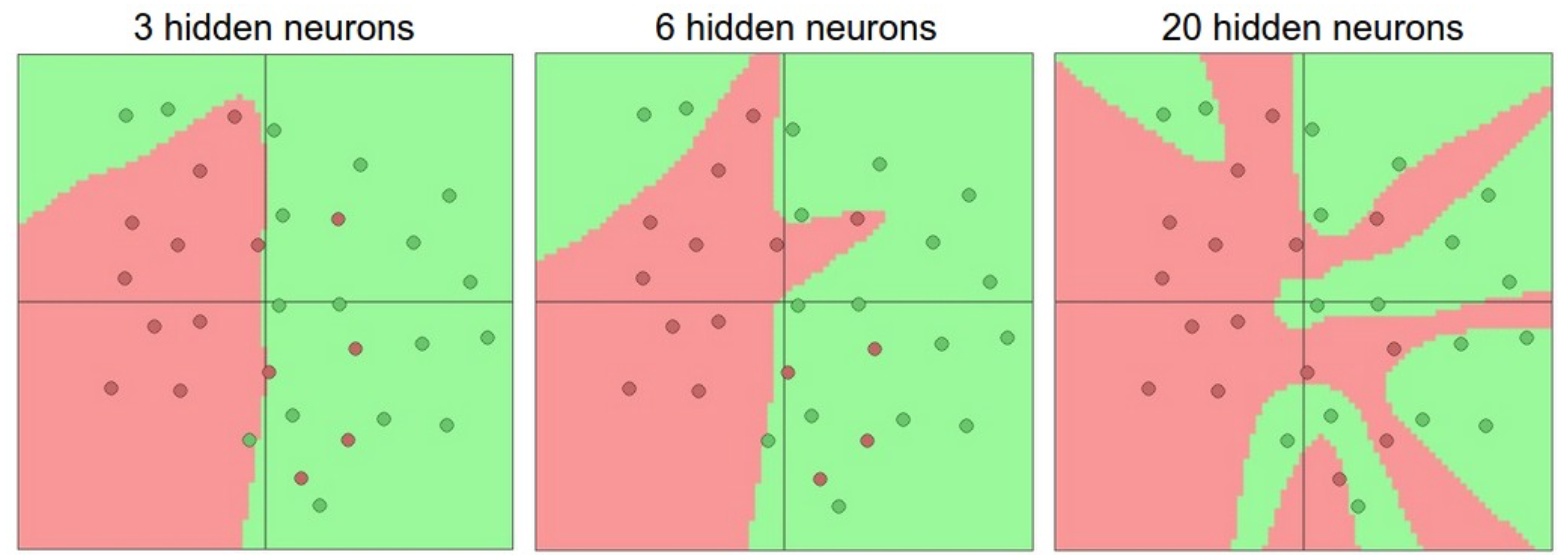
对20个神经元的网络,使用正则化,解决过拟合问题。正则化强度
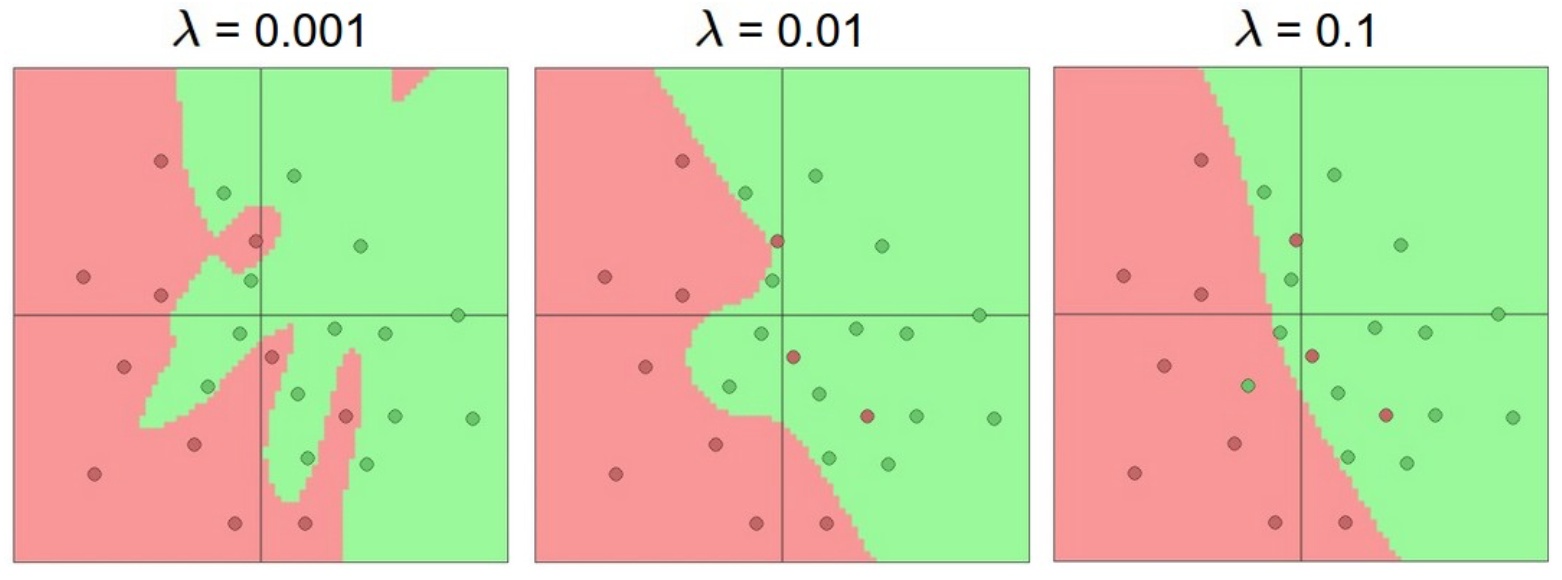
L1正则化
正则化loss如下:
对符号函数:
更新参数:
分析:
特别地:当
随机失活Dropout
Dropout是非常有用的正则化的办法,它改变了网络结构。一般采用L2正则化+Dropout来防止过拟合。
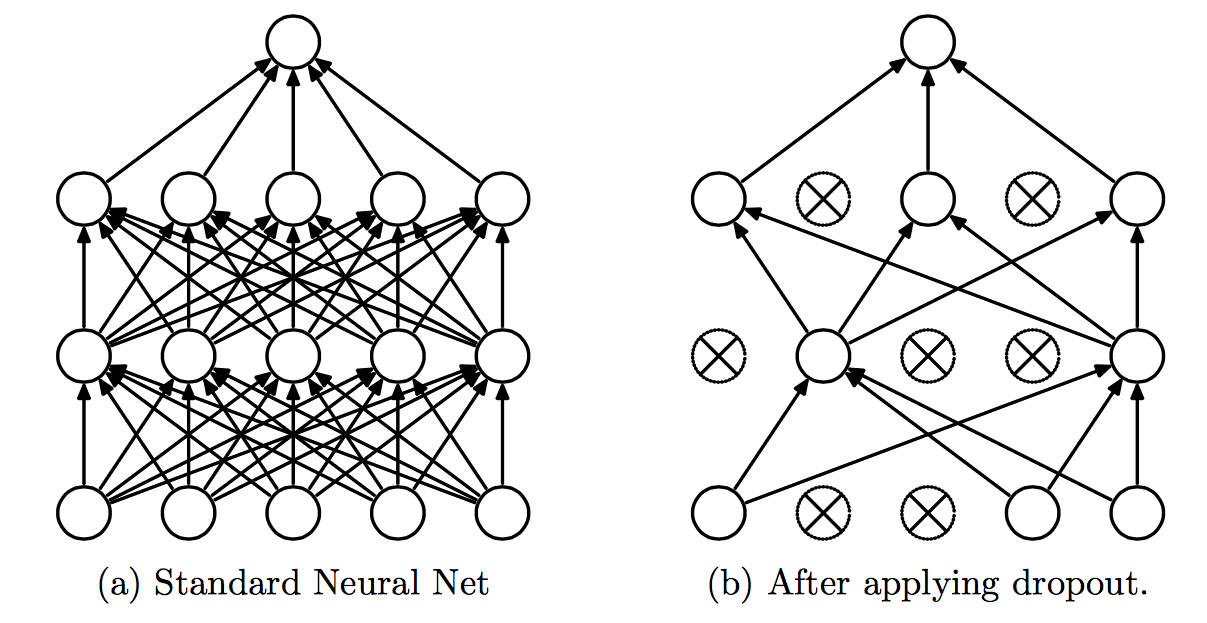
训练的时候,输出不变,随机以概率
BP的时候,置位0的神经元的参数就不再更新, 只更新前向时alive的神经元。
预测的时候,要保留所有的神经元,即不使用Dropout。
相当于训练了很多个(指数级数量)小网络(半数网络),在预测的时候综合它们的结果。随着训练的进行,大部分的半数网络都可以给出正确的分类结果。
数据预处理
用的很多的是0中心化。CNN中很少用PCA和白化。
应该:线划分训练、验证、测试集,只是从训练集中求平均值!然后各个集再减去这个平均值。
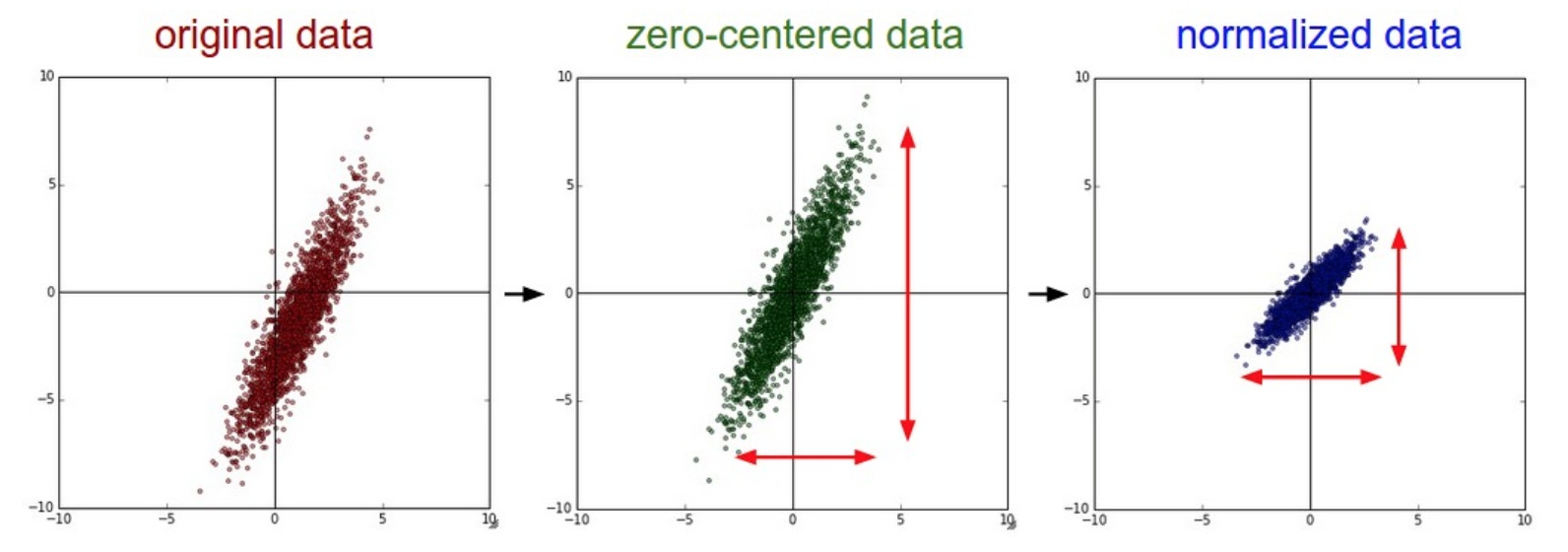
中心化
也称作均值减法, 把数据所有维度变成0均值,其实就是减去均值。就是将数据迁移到原点。
标准化
也称作归一化, 数据所有维度都归一化,使其数值变化范围都近似相等。
- 除以标准差
- 最大值和最小值按照比例缩放到
之间
方差标准差就是标准高斯分布。
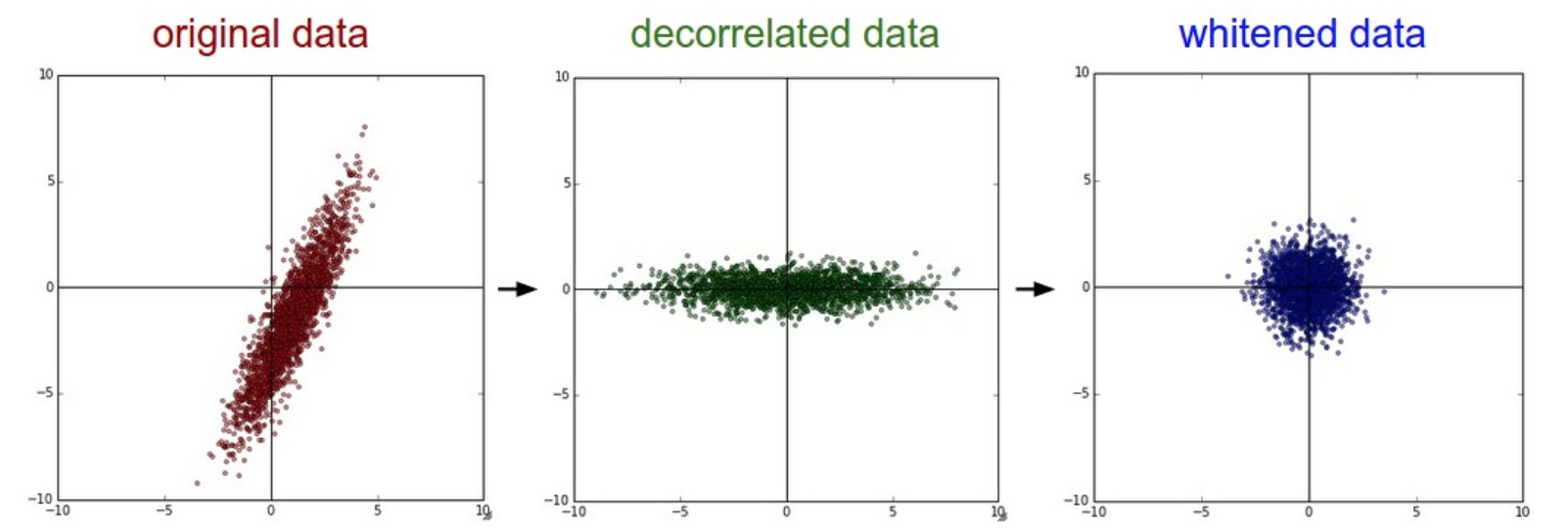
PCA
协方差
协方差就是乘积的期望-期望的乘积。
协方差的性质如下:
还有别的性质就看考研笔记吧。
奇异值分解
基向量 。是
对角矩阵。对角元素按照从小到大排列,这些对角元素称为奇异值。 是
记
利用SVD进行PCA
先将数据中心化。输入是协方差矩阵 如下:
比如X有a和b两维,均值均是0。那么
- 中心化
- 计算
的 协方差矩阵cov - 对协方差矩阵cov进行
svd分解,得到u, s, v - 去除x的相关性,旋转,
,此时xrot的协方差矩阵只有对角线才有值,其余均为0 - 选出大于0的奇异值
- 数据降维
def test_pca():
x = np.random.randn(5, 10)
# 中心化
x -= np.mean(x, axis=0)
print (x.shape)
# 协方差
conv = np.dot(x.T, x) / x.shape[0]
print (conv.shape)
print (conv)
u, s, v = np.linalg.svd(conv)
print (s)
print (u.shape, s.shape, v.shape)
# 大于0的奇异值
n_sv = np.where(s > 1e-5)[0].shape[0]
print(n_sv)
# 对数据去除相关性
xrot = np.dot(x, u)
print (xrot.shape)
# 数据降维
xrot_reduced = np.dot(x, u[:, :n_sv])
# 降到了4维
print (xrot_reduced.shape)白化
白化希望特征之间的相关性较低,所有特征具有相同的协方差。白化后,得到均值为0,协方差相等的矩阵。对
x_white = xrot / np.sqrt(s + 1e-5)缺陷是:可能会夸大数据中的早上,因为把所有维度都拉伸到了相同的数值范围。可能有一些极少差异性(方差小)但大多数是噪声的维度。可以使用平滑来解决。
权重初始化
如果数据恰当归一化以后,可以假设所有权重数值中大约一半为正数,一半为负数。所以期望参数值是0。
千万不能够全零初始化。因为每个神经元的输出相同,BP时梯度也相同,参数更新也相同。神经元之间就失去了不对称性的源头。
小随机数初始化
如果神经元刚开始的时候是随机且不相等的,那么它们将计算出不同的更新,并成为网络的不同部分。
参数接近于0单不等于0。使用零均值和标准差的高斯分布来生成随机数初始化参数,这样就打破了对称性。
W = 0.01 * np.random.randn(D,H)注意:不是参数值初始越小就一定好。参数小,意味着会减小BP中的梯度信号,在深度网络中,就会有问题。
校准方差
随着数据集的增长,随机初始化的神经元的输出数据分布的方差也会增大。可以使用
数学详细推导见cs231n ,
所以要使用
W = 0.01 * np.random.randn(D,H)/ sqrt(n)经验公式
对于某一层的方差,应该取决于两层的输入和输出神经元的数量,如下:
ReLU来说,方差应该是
W = 0.01 * np.random.randn(D,H) * sqrt(2.0 / n)稀疏和偏置初始化
一般稀疏初始化用的比较少。一般偏置都初始化为0。
Batch Normalization
莫凡python BN讲解 和 CSDN-BN论文介绍 。Batch Normalization和普通数据标准化类似,是将分散的数据标准化。
Batch Normalization在神经网络非常流行,已经成为一个标准了。
训练速度分析
网络训练的时候,每一层网络参数更新,会导致下一层输入数据分布的变化。这个称为Internal Convariate Shift。
需要对数据归一化的原因 :
- 神经网络的本质是学习数据分布。如果训练数据与测试数据的分布不同,那么
泛化能力也大大降低 - 如果每个batch数据分布不同(batch 梯度下降),每次迭代都要去学习适应不同的分布,会大大降低训练速度
深度网络,前几层数据微小变化,后面几层数据差距会积累放大。
一旦某一层网络输入数据发生改变,这层网络就需要去适应学习这个新的数据分布。如果训练数据的分布一直变化,那么就会影响网络的训练速度。
敏感度问题
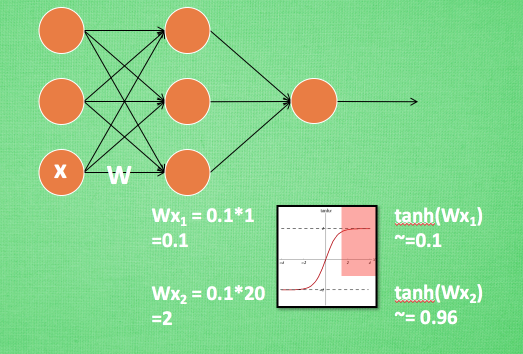
神经网络中,如果使用tanh激活函数,初始权值是0.1。
输入
但是如果一开始输入
同样地,如果再输入
对于一个变化范围比较大特征维度,神经网络在初始阶段对它已经不敏感没有区分度了!
这样的问题,在神经网络的输入层和中间层都存在。
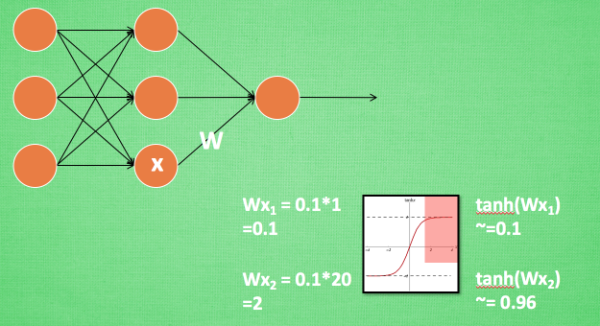
BN算法
BN算法在每一次迭代中,对每一层的输入都进行归一化。把数据转换为均值为0、方差为1的高斯分布。
非常大的缺陷:强行归一化会破坏掉刚刚学习到的特征。 把每层的数据分布都固定了,但不一定是前面一层学习到的数据分布。
牛逼的地方 :设置两个可以学习的变量扩展参数平移参数
这样理解:用这两个参数,让神经网络自己去学习琢磨是前面的标准化是否有优化作用,如果没有优化效果,就用
这样,BN就把原来不固定的数据分布,全部转换为固定的数据分布,而这种数据分布恰恰就是要学习到的分布。从而加速了网络的训练。
对一个mini-batch进行更新, 输入一个
其实就是对输入数据做个归一化:
一般在全连接层和激活函数之间添加BN层。
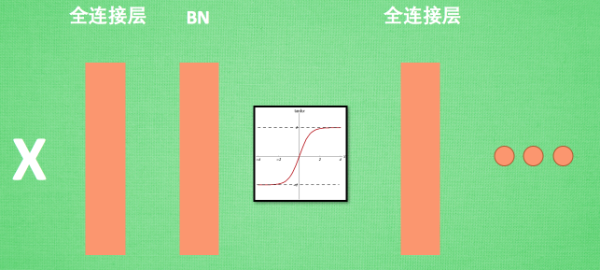
在测试的时候,由于是没有batch,所以使用固定的均值和标准差,也就是对训练的各个batch的均值和标准差做批处理。
BN的优点
1 训练速度快
2 选择大的初始学习率
初始大学习率,学习率的衰减也很快。快速训练收敛。小的学习率也可以。
3 不再需要Dropout
BN本身就可以提高网络泛化能力,可以不需要Dropout和L2正则化。源神说,现在主流的网络都没有dropout了。但是会使用L2正则化,比较小的正则化。
4 不再需要局部相应归一化
5 可以把训练数据彻底打乱
效果图片展示
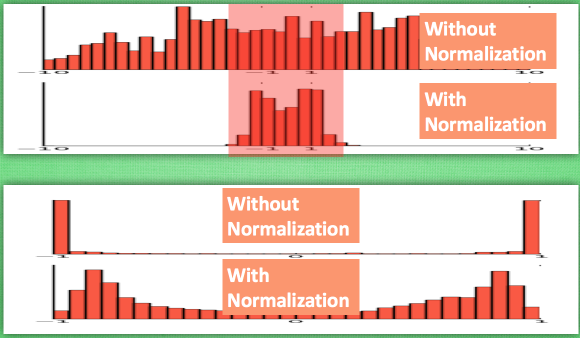
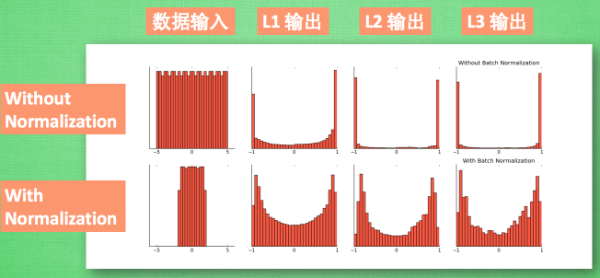
对所有数据标准化到一个范围,这样大部分的激活值都不会饱和,都不是-1或者1。
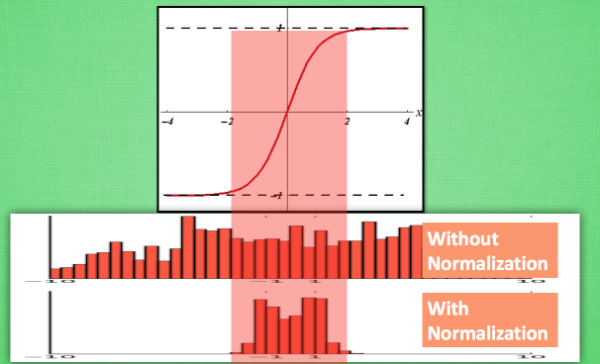
大部分的激活值在各个分布区间都有值。再传递到后面,数据更有价值。