本文包括概率图模型、马尔科夫模型和隐马尔可夫模型。重点是HMM的前后向算法、维特比算法和BW算法

概述

产生式和判别式

判别方法 由数据直接去学习决策函数$Y=f(X)$ 或者$P(Y\mid X)$作为预测模型 ，即判别模型

生成方法 先求出联合概率密度$P(X,Y)$，然后求出条件概率密度$P(Y\mid X)$。即生成模型$P(Y\mid X)=\frac{P(X,Y)}{P(X)}$

	判别式	生成式
原理	直接求$Y=f(X)$ 或$P(Y\mid X)$	先求$P(X,Y)$，然后 $P(Y\mid X)=\frac{P(X,Y)}{P(X)}$
差别	只关心差别，根据差别分类	关心数据怎么生成的，然后进行分类
应用	k近邻、感知机、决策树、LR、SVM	朴素贝叶斯、隐马尔可夫模型

概率图模型

概率图模型(probabilistic graphical models) 在概率模型的基础上，使用了基于图的方法来表示概率分布。节点表示变量，边表示变量之间的概率关系

概率图模型便于理解、降低参数、简化计算，在下文的贝叶斯网络中会进行说明。

贝叶斯网络

贝叶斯网络 又称为信度网络或者信念网络（belief networks），实际上就是一个有向无环图。

节点表示随机变量；边表示条件依存关系。没有边说明两个变量在某些情况下条件独立或者说是计算独立，有边说明任何条件下都不条件独立。

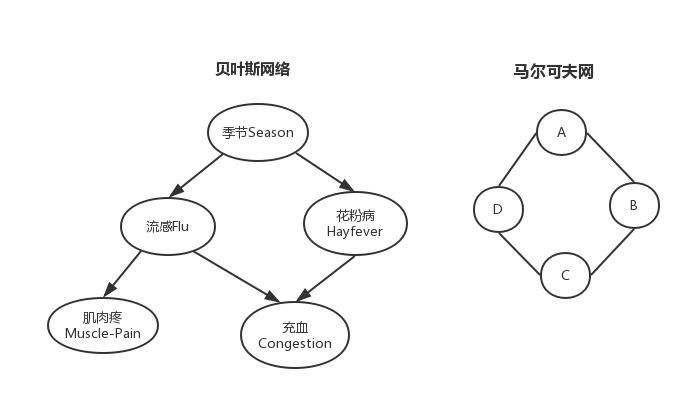
如上图所示，要表示上述情况的概率只需要求出$4\ast 2\ast 2\ast 2\ast 2-1=63$个参数的联合概率密度就行了，实际上这个太难以求得。我们可以考虑一下独立关系$(F\perp H\mid S)\mathrm{表}\mathrm{示}\mathrm{在}S\mathrm{确}\mathrm{定}\mathrm{的}\mathrm{情}\mathrm{况}\mathrm{下}，F\mathrm{和}H\mathrm{独}\mathrm{立}$，所以有以下独立关系：

$$(F\perp H\mid S)、(C\perp S\mid F,H)、(M\perp H,C\mid F)、(M\perp C|F)$$

所以我们得到如下的计算独立假设：

$$P(C\mid FHS)=P(C\mid FH)，\mathrm{即}\mathrm{假}\mathrm{设}C\mathrm{只}\mathrm{与}FH\mathrm{有}\mathrm{关}，\mathrm{而}\mathrm{与}S\mathrm{无}\mathrm{关}$$

又由$P(AB)=P(A|B)P(B)$，所以得到联合概率分布：

$$\begin{array}{rl}P(SFHMC)& =P(M\mid SHFC)\cdot P(SHFC)=\underset{\mathrm{计}\mathrm{算}\mathrm{独}\mathrm{立}\mathrm{性}}{\underbrace{P(M\mid F)}}\cdot \underset{\mathrm{继}\mathrm{续}\mathrm{分}\mathrm{解}}{\underbrace{P(C\mid SHF)\cdot P(SHF)}}\\ & =P(M\mid F)\cdot P(C\mid FH)\cdot P(F\mid S)\cdot P(H\mid S)\cdot P(S)\end{array}$$

$P(S)$ 4个季节，需要3个参数；$P(H\mid S)$时，$P(Y\mid Spring)$ 和 $P(N\mid Spring)$只需要一个参数，所以$P(H\mid S)$只需要4个参数即可，其他同理。

所以联合概率密度就转化成了上述公式中的5个乘积项，其中每一项需要的参数个数分别是2、4、4、4、3，所以一共只需要17个参数，这就大大降低了参数的个数。

马尔可夫模型

简介

马尔可夫模型(Markov Model) 描述了一类重要的随机过程，未来只依赖于现在，不依赖于过去。这样的特性的称为马尔可夫性，具有这样特性的过程称为马尔可夫过程。

时间和状态都是离散的马尔可夫过程称为马尔可夫链，简称马氏链，关键定义如下

• 系统有$N$个状态$S=\{s_1,s_2,\cdots ,s_N\}$，随着时间的推移，系统将从某一状态转移到另一状态
• 设$q_t\in S$是系统在$t$时刻的状态，$Q=\{q_q,q_2,\cdots ,q_T\}$系统时间的随机变量序列

一般地，系统在时间$t$时的状态$s_j$取决于$[1,t-1]$的所有状态$\{q_1,q_2,\cdots ,q_{t-1}\}$，则当前时间的概率是

$$P(q_t=s_j\mid q_{t-1}=s_i,q_{t-2}=s_k,\cdots )$$

在时刻$m$处于$s_i$状态，那么在时刻$m+n$转移到状态$s_j$的概率称为转移概率，即从时刻$m\to m+n$：

$$P_{ij}(m,m+n)=P(q_{m+n}=s_j\mid q_m=s_i)$$

如果$P_{ij}(m,m+n)$只与状态$i,j$和步长$n$有关，而与起始时间$m$无关，则记为$P_{ij}(n)$,称为n步转移概率。 并且称此转移概率具有平稳性，且称此链是齐次的，称为齐次马氏链，我们重点研究齐次马氏链。$P(n)=[P_{ij}(n)]$称为n步转移矩阵。

$$P_{ij}(m,m+n)=P_{ij}(n)=P(q_{m+n}=s_j\mid q_m=s_i)$$

特别地，$n=1$时，有一步转移概率如下

$$p_{ij}=P_{ij}(1)=P(q_{m+1}\mid q_m)=a_{ij}$$

一阶马尔可夫

特别地，如果**$t$时刻状态只与$t-1$时刻状态有关**，那么下有离散的一阶马尔可夫链如下：

$$P(q_t=s_j\mid q_{t-1}=s_i,q_{t-2}=s_k,\cdots )=P(q_t=s_j\mid q_{t-1}=s_i)$$

其中$t-1$的状态$s_i$转移到$t$的状态$s_j$的概率定义如下：

$$P(q_t=s_j\mid q_{t-1}=s_i)=a_{ij}，\mathrm{其}\mathrm{中}i,j\in [1,N]，a_{ij}\ge 0，\sum _{j=1}^N{a}_{ij}=1$$

显然，$N$个状态的一阶马尔可夫链有$N^2$次状态转移，这些概率$a_{ij}$构成了状态转移矩阵。

$$A=[a_{ij}]=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]$$

设系统在初始状态的概率向量是 ${\pi }_i\ge 0$ ，其中，$\sum _{i=1}^N{\pi }_i=1$

那么时间序列$Q=\{q_1,q_2,\cdots ,q_T\}$出现的概率是

$$P(q_1,q_2,\cdots ,q_T)=P(q_1)P(q2\mid q_1)P(q_3\mid q_2)\cdots P(q_T\mid q_{T-1})=\underset{\mathrm{初}\mathrm{态}\mathrm{概}\mathrm{率}}{\underbrace{{\pi }_{q_1}}}\prod _{t=1}^{T-1}{a}_{q_t{q}_{t+1}}$$

下图是一个例子

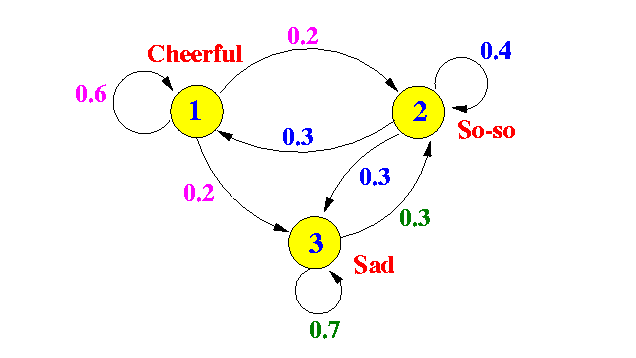
多步转移概率

对于齐次马氏链，多步转移概率就是$u+v$时间段的状态转移，可以分解为先转移$u$步，再转移$v$步。则有CK方程的矩阵形式

$$P(u+v)=P(u)P(v)$$

由此得到$n$步转移概率矩阵是一次转移概率矩阵的$n$次方

$$P(n)=P(1)P(n-1)=PP(n-1)⟹P(n)=P^n$$

对于求矩阵的幂$A^n$，则最好使用相似对角化来进行矩阵连乘。

存在一个可逆矩阵P，使得$P^{-1}AP=\mathrm{\Lambda }，A=P\mathrm{\Lambda }{P}^{-1}$，其中$\mathrm{\Lambda }$是矩阵$A$的特征值矩阵

$$\mathrm{\Lambda }=\left[\begin{array}{cccc}{\lambda }_1& & & \\ & {\lambda }_2& & \\ & & \ddots & \\ & & & {\lambda }_n\end{array}\right]，\mathrm{其}\mathrm{中}\lambda \mathrm{是}\mathrm{矩}\mathrm{阵}A\mathrm{的}\mathrm{特}\mathrm{征}\mathrm{值}$$

则有$A^n=P{\mathrm{\Lambda }}^n{P}^{-1}$

遍历性

齐次马氏链，状态$i$向状态$j$转移，经过无穷步，任何状态$s_i$经过无穷步转移到状态$s_j$的概率收敛于一个定值${\pi }_j$，即$\underset{n\to \mathrm{\infty }}{lim}{P}_{ij}(n)={\pi }_j(\mathrm{与}i\mathrm{无}\mathrm{关})$ 则称此链具有遍历性。若$\sum _{j=1}^N{\pi }_j=1$，则称$\overrightarrow{\pi }=({\pi }_1,{\pi }_2,\cdots )$为链的极限分布。

遍历性的充分条件：如果存在正整数$m$(步数)，使得对于任意的，都有如下（转移概率大于0），则该马氏链具有遍历性

$$P_{ij}(m)>0,i,j=1,2,\cdots ,N,s_i,s_j\in S$$

那么它的极限分布$\overrightarrow{\pi }=({\pi }_1,{\pi }_2,\cdots ,{\pi }_N)$，它是下面方程组的唯一解

$$\pi =\pi P,\mathrm{即}{\pi }_j=\sum _{i=1}^N{\pi }_i{p}_{ij},\mathrm{其}\mathrm{中}{\pi }_j>0,\sum _{j=1}^N{\pi }_j=1$$

PageRank应用

有很多应用，压缩算法、排队论等统计建模、语音识别、基因预测、搜索引擎鉴别网页质量-PR值。

Page Rank算法

这是Google最核心的算法，用于给每个网页价值评分，是Google“在垃圾中找黄金”的关键算法。

大致思想是要为搜索引擎返回最相关的页面。页面相关度是由和当前网页相关的一些页面决定的。

• 当前页面会把自己的importance平均传递给它所指向的页面，若有$k$个，则为每个传递$\frac{1}{k}$

• 如果有很多页面都指向当前页面，则当前页面很重要，相关度高

• 当前页面有一些来自官方页面的backlink，当前页面很重要

例如有4个页面，分别如下

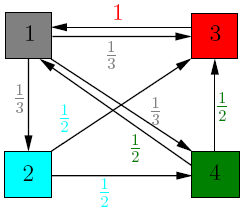
矩阵$A$是页面跳转的一次转移矩阵，$q$是当前时间每个页面的相关度向量，即PageRank vector。

$$A=\left[\begin{array}{cccc}0& 0& 1& \frac{1}{2}\\ \frac{1}{3}& 0& 0& 0\\ \frac{1}{3}& \frac{1}{2}& 0& \frac{1}{2}\\ \frac{1}{3}& \frac{1}{2}& 0& 0\end{array}\right]\mathrm{初}\mathrm{始}\mathrm{时}\mathrm{刻}，q=\left[\begin{array}{c}\frac{1}{4}\\ \frac{1}{4}\\ \frac{1}{4}\\ \frac{1}{4}\end{array}\right]$$

$A$的一列是当前页面出去的所有页面，一行是进入当前页面的所有页面。设$u$表示第$A$的第$i$行，那么$u\ast q$就表示当页面$i$接受当前$q$的更新后的rank值。

定义矩阵$G=\alpha A+(1-\alpha )\frac{1}{n}U$，对$A$进行修正，$G$所有元素大于0，具有遍历性

• $\alpha \in [0,1](\alpha =0.85)$ 阻尼因子
• $A$ 一步转移矩阵
• $n$ 页面数量
• $U$ 元素全为$1$的矩阵

使用$G$进行迭代的好处

• 解决了很多$A$元素为0导致的问题，如没有超链接的节点，不连接的图等
• $A$所有元素大于0，具有遍历性，具有极限分布，即它的极限分布$q$会收敛

那么通过迭代就可以求出PR向量$q^{next}=G{q}^{cur}$，实际上$q$是$G$的特征值为1的特征向量。

迭代具体计算如下图(下图没有使用G，是使用A去算的，这是网上找的图[捂脸])

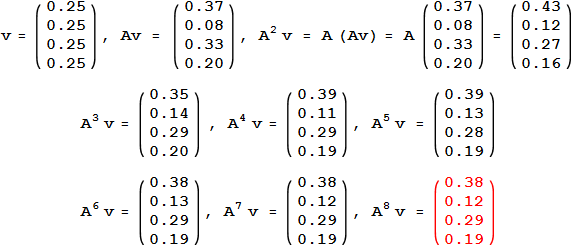
随着迭代，$q$会收敛，那么称为$q$就是PageRank vector。

我们知道节点1有2个backlink，3有3个backlink。但是节点1却比3更加相关，这是为什么呢？因为节点3虽然有3个backlink，但是却只有1个outgoing，只指向了页面1。这样的话它就把它所有的importance都传递给了1，所以页面1也就比页面3的相关度高。

隐马尔可夫模型

定义

隐马尔可夫模型（Hidden Markov Model， HMM）是统计模型，它用来描述含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数，然后利用这些参数来做进一步的分析。大概形状如下

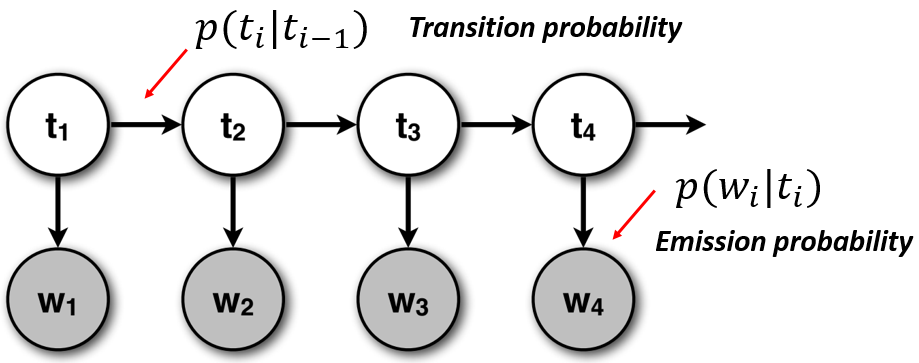
一个HMM由以下5个部分构成。

隐藏状态

• 模型的状态，隐蔽不可观察
• 有$N$种，隐状态种类集合$S=\{s_1,s_2,\cdots ,s_N\}$会相
• 隐藏状态互相互转换，一步转移。$s_i$转移到$s_j$的概率 $a_{ij}=P(q_t=s_j\mid q_{t-1}=s_i)$
• $q_t=s_i$ 代表在$t$时刻，系统隐藏状态$q_t$是$s_i$
• 隐状态时间序列 $Q=\{q_1,q_2,\cdots ,q_t,q_{t+1}\cdots \}$

观察状态

• 模型可以显示观察到的状态
• 有$M$种，显状态种类集合$K=\{v_1,v_2,\cdots ,v_M\}$。不能相互转换，只能由隐状态产生(发射)
• $o_t=v_k$ 代表在$t$时刻，系统的观察状态$o_t$是$v_k$
• 每一个隐藏状态会发射一个观察状态。$s_j$发射符号$v_k$的概率$b_j(k)=P(o_t=v_k\mid s_j)$
• 显状态时间序列 $O=\{o_1,o_2,\cdots ,o_t\}$

状态转移矩阵A (隐--隐)

• 从一个隐状$s_i$转移到另一个隐状$s_j$的概率。$A=\{a_{ij}\}$
• $a_{ij}=P(q_t=s_j\mid q_{t-1}=s_i)$，其中 $1\le i,j\le N,a_{ij}\ge 0,\sum _{j=1}^N{a}_{ij}=1$

发射概率矩阵B (隐--显)

• 一个隐状$s_j$发射出一个显状$v_k$的概率。$B=\{b_j(k)\}$
• $b_j(k)=P(o_t=v_k\mid s_j)$，其中$1\le j\le N;1\le k\le M;b_{jk}\ge 0;\sum _{k=1}^M{b}_{jk}=1$

初始状态概率分布 $\pi$

• 最初的隐状态$q_1=s_i$的概率是${\pi }_i=P(q_1=s_i)$
• 其中$1\le i\le N,{\pi }_i\ge 0,\sum _{i=1}^N{\pi }_i=1$

一般地，一个HMM记作一个五元组$\mu =(S,K,A,B,\pi )$，有时也简单记作$\mu =(A,B,\pi )$。一般，当考虑潜在事件随机生成表面事件的时候，HMM是非常有用的。

HMM中的三个问题

• 观察序列概率 给定观察序列$O=\{o_1,o_2,\cdots ,o_T\}$和模型$\mu =(A,B,\pi )$，求当前观察序列$O$的出现概率$P(O\mid \mu )$
• 状态序列概率 给定观察序列$O=\{o_1,o_2,\cdots ,o_T\}$和模型$\mu =(A,B,\pi )$，求一个最优的状态序列$Q=\{q_1,q_2,\cdots ,q_T\}$的出现概率，使得最好解释当前观察序列$O$
• 训练问题或参数估计问题 给定观察序列$O=\{o_1,o_2,\cdots ,o_T\}$，调节模型$\mu =(A,B,\pi )$参数，使得$P(O\mid u)$最大

前后向算法

给定观察序列$O=\{o_1,o_2,\cdots ,o_T\}$和模型$\mu =(A,B,\pi )$，求给定模型$\mu$的情况下观察序列$O$的出现概率。这是解码问题。如果直接去求，计算量会出现指数爆炸，那么会很不好求。我们这里使用前向算法和后向算法进行求解。

前向算法

前向变量${\alpha }_t(i)$是系统在$t$时刻，观察序列为$O=o_1{o}_2\cdots o_t$并且隐状态为$q_t=s_i$的概率，即

$${\alpha }_t(i)=P(o_1{o}_2\cdots o_t,q_t=s_i\mid \mu )$$

$P(O\mid \mu )$ 是在$t$时刻，状态$q_t=$ 所有隐状态的情况下，输出序列$O$的概率之和

$$P(O\mid \mu )=\sum _{i=1}^{N}P(O,q_t=s_i\mid \mu )=\sum _{i=1}^N{\alpha }_t(i)$$

接下来就是计算${\alpha }_t(i)$，其实是有动态规划的思想，有如下递推公式

$${\alpha }_{t+1}(j)=\underset{\mathrm{所}\mathrm{有}\mathrm{状}\mathrm{态}i\mathrm{转}\mathrm{为}j\mathrm{的}\mathrm{概}\mathrm{率}}{\underbrace{(\sum _{i=1}^N{\alpha }_t(i)a_{ij})}}\underset{\mathrm{状}\mathrm{态}j\mathrm{发}\mathrm{射}{o}_{t+1}}{\underbrace{b_j(o_{t+1})}}$$

上述计算，其实是分为了下面3步

• 从1到达时间$t$，状态为$s_i$，输出$o_1{o}_2\cdots o_t$。${\alpha }_t(i)$
• 从$t$到达$t+1$，状态变化$s_i\to s_j\text{。}{a}_{ij}$
• 在$t+1$时刻，输出$o_{t+1}$。$b_j(o_{t+1})$

算法的步骤如下

• 初始化 ${\alpha }_1(i)={\pi }_i{b}_i(o_1),1\le i\le N$
• 归纳计算 ${\alpha }_{t+1}(j)=(\sum _{i=1}^N{\alpha }_t(i)a_{ij})b_j(o_{t+1}),1\le t\le T-1$
• 求和终结 $P(O\mid \mu )=\sum _{i=1}^N{\alpha }_T(i)$

在每个时刻$t$，需要考虑$N$个状态转移到$s_j$的可能性，同时也需要计算${\alpha }_t(1),\cdots ,{\alpha }_t(N)$，所以时间复杂度为$O(N^2)$。同时在系统中有$T$个时间，所以总的复杂度为$O(N^{2}T)$。

后向算法

后向变量 ${\beta }_t(i)$ 是系统在$t$时刻，状态为$s_i$的条件下，输出为$o_{t+1}{o}_{t+2}\cdots o_T$的概率，即

$${\beta }_t(i)=P(o_{t+1}{o}_{t+2}\cdots o_T\mid q_t=s_i,\mu )$$

递推 ${\beta }_t(i)$的思路及公式如下

• 从$t\to t+1$，状态变化$s_i\to s_j$，并从$s_j⟹o_{t+1}$，发射$o_{t+1}$
• 在$q_{t+1}=s_j$的条件下，输出序列$o_{t+2}\cdots o_T$

$${\beta }_t(i)=\sum _{j=1}^N\underset{s_i\mathrm{转}{s}_j{s}_j\mathrm{发}{o}_{t+1}t+1\mathrm{时}{s}_j\mathrm{后}\mathrm{面}\{o_{t+2},\cdots \}}{\underbrace{a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}}$$

上面的公式个人的思路解释如下(不明白公式再看)

• 其实要从${\beta }_{t+1}(j)\to {\beta }_t(i)$
• ${\beta }_{t+1}(j)$是$t+1$时刻状态为$s_j$，后面的观察序列为$o_{t+2},\cdots ,o_T$
• ${\beta }_t(i)$是$t$时刻状态为$s_i$，后面的观察序列为$o_{t+1},o_{t+2},\cdots ,o_T$
• $t\to t+1$ $s_i$会变成各种$s_j$，${\beta }_t(i)$只关心t+1时刻的显示状态为$o_{t+1}$，而不关心隐状态，所以是所有隐状态发射$o_{t+1}$的概率和
• $a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)$，$s_i$转为$s_j$的概率，在t+1时刻$s_j$发射$o_{t+1}$的概率，t+1时刻状态为$s_j$ 观察序列为$o_{t+2},\cdots ,o_T$的概率
• 把上述概率加起来，就得到了t时刻为$s_i$,后面的观察为$o_{t+1},o_{t+2},\cdots ,o_T$的概率${\beta }_t(i)$

上式是把所有从$t+1\to t$的概率加起来，得到$t$的概率。算法步骤如下

• 初始化 ${\beta }_T(i)=1,1\le i\le N$
• 归纳计算 ${\beta }_t(i)=\sum _{j=1}^N{a}_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j),1\le t\le T-1;1\le i\le N$
• 求和终结 $P(O\mid \mu )=\sum _{i=1}^N{\pi }_i{b}_i(o_1){\beta }_1(i)$

前后向算法结合

模型$\mu$，观察序列$O=\{o_1,o_2,\cdots ,o_t,o_{t+1}\cdots ,o_T\}$，$t$时刻状态为$q_t=s_i$的概率如下

$$P(O,q_t=s_i\mid \mu )={\alpha }_t(i)\times {\beta }_t(i)$$

推导过程如下

$$\begin{array}{rl}P(O,q_t=s_i\mid \mu )& =P(o_1\cdots o_T,q_t=s_i\mid \mu )=P(o_1\cdots o_t,q_t=s_i,o_{t+1}\cdots o_T\mid \mu )\\ & =P(o_1\cdots o_t,q_t=s_i\mid \mu )\times P(o_{t+1}\cdots o_T\mid o_1\cdots o_t,q_t=s_i,\mu )\\ & ={\alpha }_t(i)\times P((o_{t+1}\cdots o_T\mid q_t=s_i,\mu )(\mathrm{显}\mathrm{然}{o}_1\cdots o_t\mathrm{是}\mathrm{显}\mathrm{然}\mathrm{成}\mathrm{立}\mathrm{的}，\mathrm{概}\mathrm{率}\mathrm{为}1，\mathrm{条}\mathrm{件}\mathrm{忽}\mathrm{略})\\ & ={\alpha }_t(i)\times {\beta }_t(i)\end{array}$$

所以，把$q_t$等于所有$s_i$的概率加起来就可以得到观察概率$P(O\mid \mu )$

$$P(O\mid \mu )=\sum _{i=1}^N{\alpha }_t(i)\times {\beta }_t(i),1\le t\le T$$

维特比算法

维特比(Viterbi)算法用于求解HMM的第二个问题状态序列问题。即给定观察序列$O=o_1{o}_2\cdots o_T$和模型$\mu =(A,B,\pi )$，求一个最优的状态序列$Q=q_1{q}_2\cdots q_T$。

有两种理解最优的思路。

• 使该状态序列中每一个状态都单独地具有最大概率，即${\gamma }_t(i)=P(q_t=s_i\mid O,\mu )$最大。但可能出现$a_{q_t{q}_{t+1}}=0$的情况
• 另一种是，使整个状态序列概率最大，即$P(Q\mid O,\mu )$最大。$\hat{Q}=arg\underset{Q}{max}P(Q\mid O,\mu )$

维特比变量 ${\delta }_t(i)$是，在$t$时刻，$q_t=s_i$ ，HMM沿着某一条路径到达状态$s_i$，并输出观察序列$o_1{o}_2\cdots o_t$的概率。

$${\delta }_t(i)=\arg \underset{q_1\cdots q_{t-1}}{max}P(q_1\cdots q_{t-1},q_t=s_i,o_1\cdots o_t\mid \mu )$$

递推关系

$${\delta }_{t+1}(i)=\underset{j}{max}[{\delta }_t(j)\cdot a_{ji}]\cdot b_i(o_{t+1})$$

路径记忆变量 ${\psi }_t(i)=k$ 表示$q_t=s_i,q_{t-1}=s_k$，即表示在该路径上状态$q_t=s_i$的前一个状态$q_{t-1}=s_k$。

维特比算法步骤

初始化

${\delta }_1(i)={\pi }_i{b}_i(o_1),1\le i\le N$，路径变量${\psi }_1(i)=0$

归纳计算

维特比变量 ${\delta }_t(j)=\underset{1\le i\le N}{max}[{\delta }_{t-1}(i)\cdot a_{ij}]\cdot b_j(o_t),2\le t\le T;1\le j\le N$

记忆路径(记住参数$i$就行) ${\psi }_t(j)=\arg \underset{1\le i\le N}{max}[{\delta }_{t-1}(i)\cdot a_{ij}]\cdot b_j(o_t),2\le t\le T;1\le j\le N$

终结

$$\widehat{Q_T}=\arg \underset{1\le i\le N}{max}[{\delta }_T(i)],\hat{P}(\widehat{Q_T})=\underset{1\le i\le N}{max}[{\delta }_T(i)]$$

路径（状态序列）回溯

$\widehat{q_t}={\psi }_{t+1}({\hat{q}}_{t+1}),t=T-1,T-2,\cdots ,1$

Baum-Welch算法

Baum-Welch算法用于解决HMM的第3个问题，参数估计问题，给定一个观察序列$O=o_1{o}_2\cdots o_T$，去调节模型$\mu =(A,B,\pi )$的参数使得$P(O\mid \mu )$最大化，即$\underset{\mu }{argmax}P(O_{training}\mid \mu )$。模型参数主要是$a_{ij},b_j(k)\text{和}{\pi }_i$，详细信息见上文。

有完整语料库

如果我们知道观察序列$O=o_1{o}_2\cdots o_T$和状态序列$Q=q_1{q}_2\cdots q_T$，那么我们可以根据最大似然估计去计算HMM的参数。

设$\delta (x,y)$是克罗耐克函数，当$x==y$时为1，否则为0。计算步骤如下

$$\begin{array}{rl}& \mathrm{初}\mathrm{始}\mathrm{概}\mathrm{率}{\overline{\pi }}_i=\delta (q_1,s_1)\\ & \mathrm{转}\mathrm{移}\mathrm{概}\mathrm{率}{\overline{a}}_{ij}=\frac{s_i\to s_j\mathrm{的}\mathrm{次}\mathrm{数}}{s_i\to all\mathrm{的}\mathrm{次}\mathrm{数}}=\frac{\sum _{t=1}^{T-1}\delta (q_t,s_i)\times \delta (q_{t+1},s_j)}{\sum _{t=1}^{T-1}\delta (q_t,s_i)}\\ & \mathrm{发}\mathrm{射}\mathrm{概}\mathrm{率}{\overline{b}}_j(k)=\frac{s_j\to v_k\mathrm{的}\mathrm{次}\mathrm{数}}{Q\mathrm{到}\mathrm{达}{q}_j\mathrm{的}\mathrm{次}\mathrm{数}}=\frac{\sum _{t=1}^T\delta (q_t,s_i)\times \delta (o_t,v_k)}{\sum _{t=1}^T\delta (q_t,s_j)}\end{array}$$

但是一般情况下是不知道隐藏状态序列$Q$的，还好我们可以使用期望最大算法去进行含有隐变量的参数估计。主要思路如下。

我们可以给定初始值模型${\mu }_0$，然后通过EM算法去估计隐变量$Q$的期望来代替实际出现的次数，再通过上式去进行计算新的参数得到新的模型${\mu }_1$，再如此迭代直到参数收敛。

这种迭代爬山算法可以局部地使$P(O\mid \mu )$最大化，BW算法就是具体实现这种EM算法。

Baum-Welch算法

给定HMM的参数$\mu$和观察序列$O=o_1{o}_2\cdots o_T$。

定义t时刻状态为$s_i$和t+1时刻状态为$s_j$的概率是${\xi }_t(i,j)=P(q_t=s_i,q_{t+1}=s_j\mid O,\mu )$

$$\begin{array}{rl}{\xi }_t(i,j)& =\frac{P(q_t=s_i,q_{t+1}=s_j,O\mid \mu )}{P(O\mid \mu )}=\frac{{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}{P(O\mid \mu )}=\frac{\stackrel{o_1\cdots o_t,o_{t+1},o_{t+2}\cdots o_T}{\overbrace{{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}}}{\underset{{\xi }_t(i,j)\mathrm{对}ij\mathrm{求}\mathrm{和}，\mathrm{只}\mathrm{留}\mathrm{下}P(O\mid \mu )}{\underbrace{\sum _{i=1}^N\sum _{j=1}^N{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}}}\end{array}$$

定义**$t$时刻状态为$s_i$的概率**是${\gamma }_t(i)=P(q_t=s_i\mid O,\mu )$

$${\gamma }_t(i)=\sum _{j=1}^N{\xi }_t(i,j)$$

那么有算法步骤如下（也称作前向后向算法）

1初始化

随机地给参数$a_{ij},b_j(k),{\pi }_i$赋值，当然要满足一些基本条件，各个概率和为1。得到模型${\mu }_0$，令$i=0$，执行下面步骤

2EM步骤

2.1E步骤 使用模型${\mu }_i$计算${\xi }_t(i,j)\mathrm{和}{\gamma }_t(i)$

$${\xi }_t(i,j)=\frac{{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)}{\sum _{i=1}^N\sum _{j=1}^N{\alpha }_t(i)a_{ij}{b}_j(o_{t+1}){\beta }_{t+1}(j)},{\gamma }_t(i)=\sum _{j=1}^N{\xi }_t(i,j)$$

2.2M步骤 用上面算得的期望去估计参数

$$\begin{array}{rl}& \mathrm{初}\mathrm{始}\mathrm{概}\mathrm{率}{\overline{\pi }}_i=P(q_1=s_i\mid O,\mu )={\gamma }_1(i)\\ & \mathrm{转}\mathrm{移}\mathrm{概}\mathrm{率}{\overline{a}}_{ij}=\frac{\sum _{t=1}^{T-1}{\xi }_t(i,j)}{\sum _{t=1}^{T-1}{\gamma }_t(i)}\\ & \mathrm{发}\mathrm{射}\mathrm{概}\mathrm{率}{\overline{b}}_j(k)=\frac{\sum _{t=1}^T{\gamma }_t(j)\times \delta (o_t,v_k)}{\sum _{t=1}^T{\gamma }_t(j)}\end{array}$$

3循环计算 令$i=i+1$，直到参数收敛