本文简单记录了EM算法的思想和Jensen不等式

EM算法定义

背景

如果概率模型的变量都是观测变量，那么可以直接使用极大似然估计法或贝叶斯估计法去估计模型参数。

如果模型既有观测变量又有隐变量，就不能简单使用上述方法。

EM算法，期望极大算法，就是含有隐变量的概率模型参数的极大似然估计法或极大后验概率估计法，是一种迭代算法。每次迭代分为如下两步

• E步：求期望(expectation)
• M步：求极大(maximization)

三硬币模型

有3枚硬币，记做ABC，每次出现正面的概率分别是$\pi ,p,q$。先掷A，正面选B，反面选C。再掷B/C，得到正面1或反面0作为一次的结果。问：去估计参数$\theta =(\pi ,p,q)$

• 观察变量：一次 实验得到的结果1或0，记做$y$
• 隐变量：A的结果，即掷的是B还是C，记做$z$

对于一次实验，求出$y$的概率分布

$$\begin{array}{rl}P(y\mid \theta )& =\underset{\mathrm{把}\mathrm{所}\mathrm{有}z\mathrm{的}y\mathrm{加}\mathrm{起}\mathrm{来}}{\underbrace{\sum _{z}P(y,z\mid \theta )}}=\sum _z\underset{\mathrm{贝}\mathrm{叶}\mathrm{斯}\mathrm{公}\mathrm{式}}{\underbrace{P(z\mid \theta )P(y\mid z,\theta )}}=\underset{z=1\mathrm{时}}{\underbrace{\pi p^y(1-p{)}^{1-y}}}+\underset{z=0\mathrm{时}}{\underbrace{(1-\pi )q^y(1-q{)}^{1-y}}}\end{array}$$

设观察序列$Y=(y_1,y_2,\cdots ,y_n{)}^T$，隐藏数据$Z=(z_1,z_2,\cdots ,z_n{)}^T$，则观测数据的似然函数为

$$\begin{array}{rl}P(Y\mid \theta )& =\sum _{Z}P(Z\mid \theta )P(Y\mid Z,\theta )\\ & =\prod _{i=1}^n[\pi p^{y_i}(1-p{)}^{1-y_i}+(1-\pi )q^{y_i}(1-q{)}^{1-y_i}]\end{array}$$

求模型参数$\theta =(\pi ,p,q)$的最大似然估计，即

$$\hat{\theta }=argma{x}_{\theta }\log P(Y\mid \theta )$$

这个问题不能直接求解，只有通过迭代的方法求解。EM算法就是解决这种问题的一种迭代算法。先给${\theta }^{(0)}$ 选择初始值，然后去迭代。每次迭代分为E步和M步。

EM算法

基本概念

一些概念如下

• $Y$ 观测变量，$Z$ 隐变量
• 不完全数据：$Y$；概率分布：$P(Y\mid \theta )$；对数似然函数：$L(\theta )=\log P(Y\mid \theta )$
• 完全数据：$Y$和$Z$合在一起；概率分布：$P(Y,Z\mid \theta )$；对数似然函数：$\log P(Y,Z\mid \theta )$

EM算法通过迭代求$L(\theta )=\log P(Y\mid \theta )$的极大似然估计。

概率论函数的期望

设$Y$是随机变量$X$的函数，$Y=g(X)$，$g$是连续函数，那么

$X$是离散型变量，$X$的分布律为$P(X=x_i)=p_i,i=1,2,3\cdots$，则有

$$E(Y)=E(g(X))=\sum _{i=1}^{\mathrm{\infty }}g(x_i)p_i,\mathrm{左}\mathrm{式}\mathrm{收}\mathrm{敛}\mathrm{时}\mathrm{成}\mathrm{立}$$

$X$是 连续型变量，$X$的概率密度为$f(x)$，则有

$$E(Y)=E(g(X))={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}g(x)f(x)\mathrm{d}x,\mathrm{左}\mathrm{式}\mathrm{绝}\mathrm{对}\mathrm{收}\mathrm{敛}\mathrm{成}\mathrm{立}$$

Q函数

$Q(\theta ,{\theta }^{(i)})$是EM算法的核心。它是完全数据的对数似然函数$\log P(Y,Z\mid \theta )$的期望，是关于未观测数据$Z$的条件概率分布$P(Z\mid Y,{\theta }^{(i)})$，而$Z$的条件是在给定观测数据$Y$和当前参数${\theta }^{(i)}$。（都是后置定语，不通顺）

$$\begin{array}{rl}Q(\theta ,{\theta }^{(i)})& =E_Z[\log P(Y,Z\mid \theta )\mid Y,{\theta }^{(i)}]=\sum _Z\log P(Y,Z\mid \theta )P(Z\mid Y,{\theta }^{(i)})\end{array}$$

下面是我具体的理解

• ${\theta }^{(i)}$是第$i$次迭代参数$\theta$的估计值

• $P(Z\mid Y,{\theta }^{(i)})$是以$Y$和当前参数${\theta }^{(i)}$的条件下的分布律，简写为$P(Z)$。类似于上面的$X$

• $P(Y,Z\mid \theta )$ 是在以$\theta$为参数的分布的联合概率密度，简写为$P(Y,Z)$。类似于上面的$Y=g(X)$

• 求对数似然函数$\log P(Y,Z)$的期望，转移到隐变量$Z$上

• 把目标函数映射到$Z$上，$g(z)=\log P(Y,Z)$，$E(g(z))=\sum _z\log P(Y,Z)P(Z)$

• $Q(\theta ,{\theta }^{(i)})$ 是因为要找到一个新的$\theta$优于之前的${\theta }^{(i)}$，是代表的分布优于

EM算法步骤

输入：$Y$ 观测变量，$Z$ 隐藏变量，$P(Y,Z\mid \theta )$ 联合分布，条件分布 $P(Z\mid Y,\theta )$

输出：模型参数$\theta$

步骤

• 选择参数初始值${\theta }^{(0)}$，开始迭代
• E步：第$i+1$次迭代， 求 $Q(\theta ,{\theta }^{(i)})=\sum _Z\log P(Y,Z\mid \theta )P(Z\mid Y,{\theta }^{(i)})$
• M步：求使$Q(\theta ,{\theta }^{(i)})$极大化的$\theta$，得到$i+1$次迭代新的估计值${\theta }^{(i+1)}=argma{x}_{\theta }(Q(\theta ,{\theta }^{(i)}))$
• 重复E和M步，直到收敛

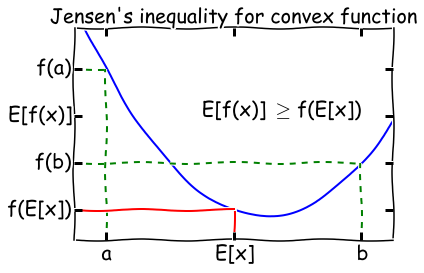
Jensen不等式

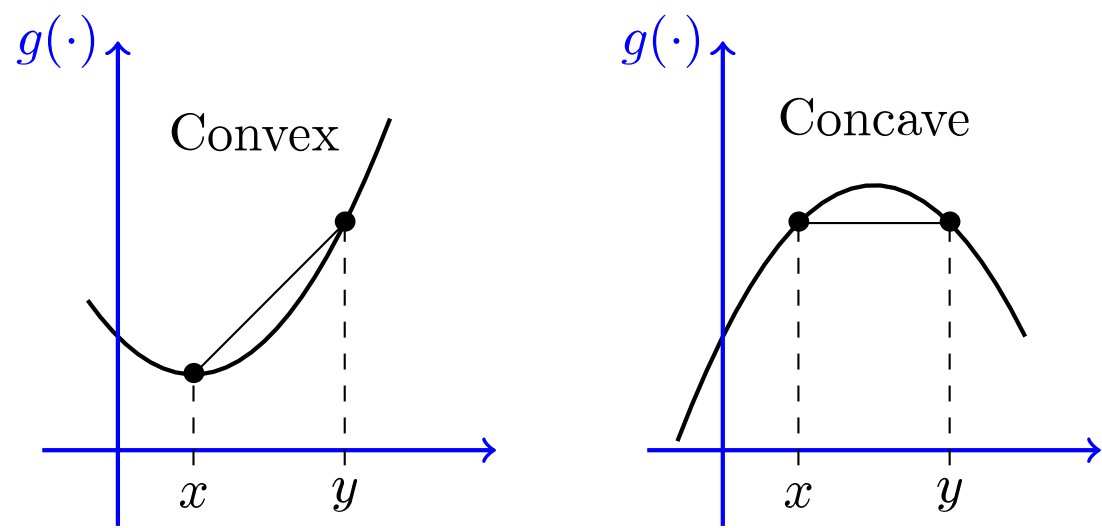
凸函数与凹函数

从图像上讲，在函数上两点连接一条直线。直线完全在图像上面，就是凸函数 convex；完全在下面，就是凹函数 concave。

$f^{\prime \prime }(x)\ge 0⟹f(x)\mathrm{是}\mathrm{凸}\mathrm{函}\mathrm{数};f^{\prime \prime }(x)\le 0⟹f(x)\mathrm{是}\mathrm{凹}\mathrm{函}\mathrm{数}$

Jensen不等式

函数$f(x)$，上有两点$x_1,x_2$，对于任意$\lambda \in [0,1]$

• 如果$f(x)$是凸函数，$f(\lambda x_1+(1-\lambda )x_2)\le \lambda f(x_1)+(1-\lambda )f(x_2)$
• 如果$f(x)$是凹函数，$f(\lambda x_1+(1-\lambda )x_2)\ge \lambda f(x_1)+(1-\lambda )f(x_2)$

一般地，$n$个点$x_1,x_2,\cdots ,x_n$和参数${\lambda }_1+{\lambda }_2+\cdots +{\lambda }_n=1$，对于凸函数，则有

$$f(\underset{E[X],\mathrm{总}\mathrm{体}\mathrm{是}f(E[X])}{\underbrace{{\lambda }_1{x}_1+{\lambda }_2{x}_2+\cdots +{\lambda }_n{x}_n}})\le \underset{E[f(X)]}{\underbrace{f({\lambda }_1{x}_1)+f({\lambda }_2{x}_2)+\cdots +f({\lambda }_n{x}_n)}},\mathrm{即}f(\sum _{i=1}^n{\lambda }_i{x}_i)\le \sum _{i=1}^{n}f({\lambda }_i{x}_i)$$

琴声不等式

• 凸函数 $f(E[X])\le E[f(X)]$，即$f(\sum _{i=1}^n{\lambda }_i{x}_i)\le \sum _{i=1}^{n}f({\lambda }_i{x}_i)$
• 凹函数 $f(E[X])\ge E[f(X)]$，即$f(\sum _{i=1}^n{\lambda }_i{x}_i)\ge \sum _{i=1}^{n}f({\lambda }_i{x}_i)$