条件随机场(Conditional Random Field, CRF)是给定一组输入随机变量条件下另一组输出随机变量的条件概率分布模型。常常用于标注问题。隐马尔科夫模型和条件随机场是自然语言处理中最重要的算法。CRF最重要的就是根据观测序列，把标记序列给推测出来。

概率无向图模型

概率无向图模型又称为马尔科夫随机场，是一个可以由无向图表示的联合概率分布。一些类似内容。

有一组随机变量$Y\in \mathrm{\Gamma }$，联合概率分布为$P(Y)$，由图$G=(V,E)$表示。节点v代表变量$Y_v$，节点之间的边代表两个变量的概率依赖关系。

定义

马尔可夫性就是说，给定一些条件下，没有连接的节点之间是条件独立的。

成对马尔可夫性

设$u$和$v$是两个没有边连接的节点，其它所有节点为$O$。成对马尔可夫性是说，给定随机变量组$Y_O$的条件下，随机变量$Y_u$和$Y_v$是独立的。即有如下：

$$P(Y_u,Y_v\mid Y_O)=P(Y_u\mid Y_O)P(Y_v\mid Y_O)$$

局部马尔可夫性

节点$v$，$W$是与$v$连接的所有节点，$O$是与$v$没有连接的节点。局部马尔可夫性认为，给定$Y_w$的条件下，$Y_v$和$Y_O$独立。即有：

$$P(Y_v,Y_O\mid Y_W)=P(Y_v\mid Y_W)P(Y_O\mid Y_W)$$

全局马尔可夫性

节点集合$A$，$B$被中间节点集合$C$分隔开，即不相连。全局马尔可夫性认为，给定$Y_C$的条件下，$Y_A$和$Y_B$是独立的。即有：

$$P(Y_A,Y_B\mid Y_C)=P(Y_A\mid Y_C)P(Y_B\mid Y_C)$$

上面的3个马尔可夫性的定义是等价的。

概率无向图模型

设有联合概率密度$P(Y)$，由无向图$G=(V,E)$表示。节点表示随机变量，边表示随机变量之间的依赖关系。如果联合概率密度$P(Y)$满足马尔可夫性，那么就称此联合概率分布为概率图模型，或马尔可夫随机场。

实际上我们更关心怎么求联合概率密度，一般是把整体的联合概率写成若干个子联合概率的乘积，即进行因子分解。概率无向图模型最大的优点就是易于因子分解。

概率无向图因子分解

团与最大团

团：无向图中的一个子集，任何两个节点均有边连接。

最大团：无向图中的一个子集，任何两个节点均有边连接。不能再加入一个节点组成更大的团了。

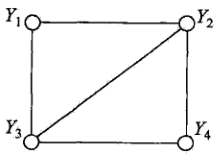
如$\{Y_1,Y_2\}$，$\{Y_1,Y_2,Y_3\}$ 都是团，其中后者是最大团。而$\{Y_1,Y_2,Y_3,Y_4\}$ 不是团，因为$Y_1$和$Y_4$没有边连接。

因子分解

有无向图模型$G$, $C$ 是 $G$ 上的最大团，有很多个。$Y_C$ 是$C$ 对应的随机变量。则联合概率分布$P(Y)$ 可以写成多个最大团$C$ 上的势函数的乘积。

$$P(Y)=\frac{1}{Z}\prod _C{\mathrm{\Psi }}_C(Y_C),Z=\sum _Y\prod _C{\mathrm{\Psi }}_C(Y_C)$$

其中$Z$是规范化因子。${\mathrm{\Psi }}_C(Y_C)$是 势函数，是一个严格正函数。等式左右两端都取条件概率也是可以的。下文就是。

$${\mathrm{\Psi }}_C(Y_C)=\exp (-E(Y_C))$$

其中$E(Y_C)$ 是能量函数。

条件随机场的定义与形式

HMM的问题

这里是HMM的讲解 。HMM有下面几个问题

• 需要给出隐状态和观察符号的联合概率分布，即发射概率 $b_j(k)$，是生成式模型，也是它们的通病。
• 观察符号需要是离散的，可以枚举的，要遍历所有观察符号。如果是一个连续序列，则不行。
• 观察符号是独立的，没有观察相互之间的依赖关系。如一个句子的前后，都有关联才是。即输出独立性假设问题。
• 无法考虑除了字词顺序以外的其它特征。比如字母为大小写，包含数字等。
• 标注偏置问题。

标注偏置问题，举例，是说有两个单词"rib-123"和"rob-456"，"ri"应该标记为"12"，"ro"应该标记为"45"。

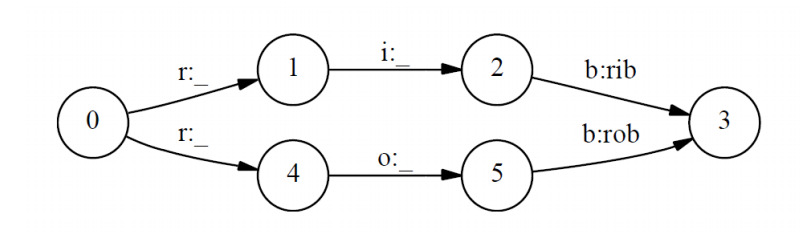$$ \begin {align} & P(12 \mid ri) = P(1 \mid r)P(2 \mid i, r=1) = P(1 \mid r) \cdot 1 = P(1 \mid r) \\ & P(45 \mid ro) = P(4 \mid r)P(5 \mid o, r=4) = P(4 \mid r) \cdot 1 = P(4 \mid r) \\ \end {align} $$ 由上面计算概率可知，ri标为12和 ro标为45的概率最终变成r标为1和4的概率。但是由于语料库中"rob"的出现次数很多，所以$P(4 \mid r) > P(1 \mid r)$ ，所以可能会一直把"rib"中的"i"标记为1，会导致标记出错。这就是标记偏置问题。

定义

条件随机场是给定随机变量$X$条件下，随机变量$Y$ 的马尔可夫随机场。我们主要关心线性链随机场，它可以用于标注问题。

条件随机场

$X$与$Y$是随机变量，条件概率分布$P(Y\mid X)$。随机变量$Y$可以构成一个无向图表示的马尔可夫随机场。任意一节点$Y_v$，$Y_A$是与$v$相连接的节点，$Y_B$是除了$v$以外的所有节点。若都有

$$P(Y_v\mid X,Y_B)=P(Y_v\mid X,Y_A)$$

则称$P(Y\mid X)$ 为条件随机场。并不要求$X$和$Y$ 具有相同的结构。

线性链条件随机场

$X$和$Y$ 有相同的线性结构。设$X=(X_1,X_2,\cdots ,X_n)$，$Y=(Y_1,Y_2,\cdots ,Y_n)$均为线性链表示的随机变量序列。每个最大团包含2个节点。

$P(Y\mid X)$ 构成条件随机场，即满足马尔可夫性

$$P(Y_i\mid X,Y_1,\cdots ,Y_{i-1},Y_{i+1},\cdots ,Y_n)=P(Y_i\mid X,Y_{i-1},Y_{i+1}),i=1,\cdots ,n。(1\mathrm{和}n\mathrm{时}\mathrm{只}\mathrm{考}\mathrm{虑}\mathrm{单}\mathrm{边})$$

则称$P(Y\mid X)$为线性链条件随机场。

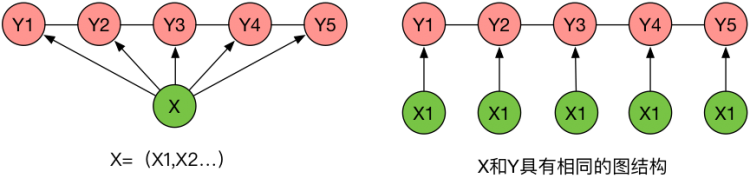
HMM，每个观察状态只与当前的隐状态有关系，分离了关系。就像1个字1个字地向后讲。输出观察符号还需要条件独立。

线性链条件随机场， 每个状态都与整个序列有关系。即先想好了整句话，再依照相应的次序去说出来。更加直击语言模型的核心。$X_1,X_2$ 不需要条件独立。

基本形式

两种特征函数

状态转移特征函数t，只依赖与当前和前一个位置，即$y_i$和$y_{i-1}$。一般是01函数。

$$t(y_{i-1},y_i,x,i)=\{\begin{array}{ll}1,& \mathrm{满}\mathrm{足}\mathrm{某}\mathrm{种}\mathrm{条}\mathrm{件},i\in [2,n].\mathrm{例}\mathrm{如}{y}_{i-1}+y_i=3\\ 0,& \mathrm{其}\mathrm{他}\end{array}$$

状态特征函数s，只依赖与当前位置$y_i$

$$s(y_i,x,i)=\{\begin{array}{ll}1,& \mathrm{满}\mathrm{足}\mathrm{某}\mathrm{种}\mathrm{条}\mathrm{件},i\in [1,n].\mathrm{例}\mathrm{如}{y}_i\mathrm{是}\mathrm{偶}\mathrm{数}\\ 0,& \mathrm{其}\mathrm{他}\end{array}$$

基础形式

设有$K_1$个状态特征转移函数，$K_2$个状态特征函数。分别对应的权值是${\lambda }_{k_1}$和${\mu }_{k_2}$。则线性链条件随机场参数化形式$P(y\mid x)$ 如下：

$$P(y\mid x)=\frac{1}{Z(x)}\exp (\sum _k^{K_1}{\lambda }_k\sum _{i=2}^n{t}_k(y_{i-1},y_i,x,i)+\sum _k^{K_2}{\mu }_k\sum _{i=1}^n{s}_k(y_i,x,i))$$

其中$Z(x)$是规范化因子，如下

$$Z(x)=\sum _x\exp (\sum _k^{K_1}{\lambda }_k\sum _{i=2}^n{t}_k(y_{i-1},y_i,x,i)+\sum _k^{K_2}{\mu }_k\sum _{i=1}^n{s}_k(y_i,x,i))$$

条件随机场完全由特征函数$t_{k_1}$ 、$s_{k_2}$，和对应的权值${\lambda }_{k_1}$ 和${\mu }_{k_2}$ 决定的。 特征函数实际上也是势函数。

简化形式

有$K=K_1+K_2$个特征，特征函数如下：

$$f_k(y_{i-1},y_i,i)=\{\begin{array}{ll}{t}_k(y_{i-1},y_i,x,i)& k=1,\cdots ,K_1\\ s_k(y_i,x,i)& k=K_1+l;l=1,\cdots ,K_2\end{array}$$

同一个特征函数，要在整个$Y$序列的各个位置进行计算，可以进行求和，即转化为全局特征函数， **新的特征函数$f_k(y,x)$**如下：

$$f_k(y,x)=\sum _{i=1}^n{f}_k(y_{i-1},y_i,i),k=1,\cdots ,K$$

$f_k(y,x)$ 对应的**新的权值$w_k$**如下

$$w_k=\{\begin{array}{ll}{\lambda }_k,& k=1,\cdots ,K_1\\ {\mu }_{k-K_1},& k=K_1+1,K_1+2,\cdots ,K\end{array}$$

所以新的条件随机场形式如下：

$$P(y\mid x)=\frac{1}{Z(x)}\exp \sum _{k=1}^K{w}_k{f}_k(y,x),Z(x)=\sum _y\exp \sum _{k=1}^K{w}_k{f}_k(y,x)$$

可以看出，格式和最大熵模型很像。条件随机场最重要的就是，根据观察序列，把标记序列给推测出来。

向量形式

向量化特征函数和权值

$$F(y,x)=(f_1(y,x),\cdots ,f_K(y,x){)}^T,w=(w_1,\cdots ,w_K{)}^T$$

可以写成向量内积的形式

$$P_w(y\mid x)=\frac{1}{Z(x)}\exp (w\cdot F(y,x)),Z(x)=\sum _y\exp (w\cdot F(y,x))$$

矩阵形式

为状态序列$Y$设置起点和终点标记，$y_0=start$ 和$y_{n+1}=stop$。从$0\to n+1$中，有$n+1$次的状态转移。我们可以用$n+1$ 个状态转移矩阵来表示状态转移的概率。

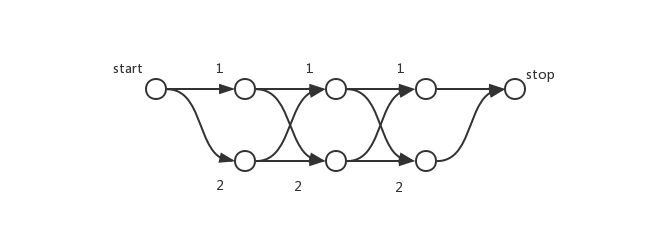
设$M_i(x)$ 是$i-1\to i$的转移矩阵，是$m$阶，$m$ 是$y_i$ 取值的个数。表示了各种取值情况互相转化的概率。

$$M_1(x)=\left[\begin{array}{cc}{a}_{01}& a_{02}\\ 0& 0\end{array}\right],M_2(x)=\left[\begin{array}{cc}{b}_{11}& b_{12}\\ b_{21}& b_{22}\end{array}\right],M_3(x)=\left[\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}\right],M_4(x)=\left[\begin{array}{cc}1& 0\\ 1& 0\end{array}\right]$$

要求什么样的路径概率，则相乘相应的数值概率即可。那么这些矩阵里面的数值是怎么来的呢。有下面的矩阵定义 ：

$$g(y_{i-1},y_i,x,i)=M_i(y_{i-1},y_i\mid x)=\exp \sum _{k=1}^K{w}_k{f}_k(y_{i-1},y_i,i,x),M_i(x)=[g(y_{i-1},y_i,x,i)]$$

每一步转移的时候，由于$(y_{i-1},y_i)$ 有$m^2$ 种情况，计算$g$时会得到多个值，即可得到一个矩阵。

其中$g(y_{i-1},y_i,x,i)$ 在计算的时候，会根据$i$ 的不同，而选择不同的特征函数进行计算。不要忘记了$f_k$函数的定义。

$$f_k(y_{i-1},y_i,i)=\{\begin{array}{ll}{t}_k(y_{i-1},y_i,x,i)& k=1,\cdots ,K_1\\ s_k(y_i,x,i)& k=K_1+l;l=1,\cdots ,K_2\end{array}$$

所以非规范化条件概率可以通过矩阵的某些元素的乘积表示，有

$$P_w(y\mid x)=\frac{1}{Z_w(x)}\prod _{i=1}^{n+1}{M}_i(y_{i-1},y_i\mid x)$$

其中规范化因子 是**$n+1$的矩阵相乘的结果矩阵中，第$(start,stop)$ 元素。例如第$(0,0)$。其中是$(start,end)$ 是矩阵下标对应**。

条件随机场的概率计算问题

主要问题是给定条件随机场$P(Y\mid X)$ ，给定输入序列$x$ 和输出序列$y$，求$P(Y_i=y_i\mid x)$ 和$P(Y_{i-1}=y_{i-1},Y_i=y_i\mid X)$， 以及相应的期望问题。

关键是求这些特征函数期望值，当模型训练好之后，去验证我们的模型。

前向后向算法

$y_i$ 确定后， ${\alpha }_i(y_i\mid x)$ 表示，从$start\to i$，就是$y = (start, y_1, \cdots, y_i) $ 的概率，也就是从前面到位置$y_i$ 的概率。特别地

$${\alpha }_0(y\mid x)=\{\begin{array}{ll}1,& y=start\\ 0,& \mathrm{其}\mathrm{他}\end{array}$$

而$y_i$ 的取值有$m$ 种， 所以前向变量 ${\alpha }_i(x)$ 到$y$ 到第 $i$ 个位置 的所有概率取值向量。

$${\alpha }_i^T(x)={\alpha }_{i-1}^T(x)\cdot M_i(x),i=1,2,\cdots ,n+1$$

$y_i$ 确定后， ${\beta }_i(y_i\mid x)$ 表示，位置$i$的标记为$y_i$ ，并且后面为$y_{i+1},\cdots ,y_n,stop$ 的概率。同理一个是概率值。特别地

$${\beta }_{n+1}(y\mid x)=\{\begin{array}{ll}1,& y=stop\\ 0,& \mathrm{其}\mathrm{他}\end{array}$$

后向变量 ${\beta }_i(y\mid x)$，是一个m维向量

$${\beta }_i(x)=M_{i+1}(x)\cdot {\beta }_{i+1}(x)$$

可以得到$Z(x)$：

$$Z(x)={\alpha }_n^T(x)\cdot 1=1^T\cdot {\beta }_{i+1}(x)$$

条件概率计算

位置是$i$ 标记$y_i$ 的条件概率$P(Y_i=y_i\mid x)$是

$$P(Y_i=y_i\mid x)=\frac{1}{Z(x)}\cdot {\alpha }_i(y_i\mid x){\beta }_i(y_i\mid x)$$

位置$i-1,i$ 分别标记为$y_{i-1},y_i$ 的概率是

$$P(Y_{i-1}=y_{i-1},Y_i=y_i\mid x)=\frac{1}{Z(x)}\cdot {\alpha }_{i-1}(y_{i-1}\mid x)M_i(y_{i-1},y_i\mid x){\beta }_i(y_i\mid x)$$

特征期望值计算

两个期望值和最大熵模型的约束条件等式 有点像。

特征函数$f_k$ 关于条件概率分布$P(Y\mid X)$ 的概率

$$E_{P(Y\mid X)}(f_k)=\sum _{y}P(y\mid x)f_k(y,x)=\sum _{i=1}^{n+1}\sum _{y_{i-1}{y}_i}{f}_k(y_{i-1},y_i,x,i)P(y_{i-1},y_i\mid x)$$

特征函数$f_k$ 关于条件概率分布$P(X,Y)$ 的概率，$\hat{P}(x)$ 是经验分布

$$E_{P(X,Y)}(f_k)=\sum _{x,y}P(x,y)\sum _{i=1}^{n+1}{f}_k(y_{i-1},y_i,x,i)=\sum _x\hat{P}(x)\sum _{y}P(y\mid x)\sum _{i=1}^{n+1}{f}_k(y_{i-1},y_i,x,i)$$

通过前向和后向向量可以计算出两个概率，然后可以计算出相应的期望值。就可以与我们训练出的模型进行比较。

学习算法

条件随机场模型实际上是定义在时序数据上的对数线性模型，学习方法有极大似然估计和正则化的极大似然估计。具体的优化实现算法有：改进的迭代尺度法IIS、梯度下降法和拟牛顿法。

改进的迭代尺度法

这里是最大熵模型中的改进的迭代尺度算法。每次更新一个${\delta }_i$ 使得似然函数的该变量的下界增大，即似然函数增大。

已知经验分布$\hat{P}(X,Y)$，和模型如下

$$P(y\mid x)=\frac{1}{Z(x)}\exp \sum _{k=1}^K{w}_k{f}_k(y,x),Z(x)=\sum _y\exp \sum _{k=1}^K{w}_k{f}_k(y,x)$$

对数似然函数和最大熵算法的极大似然函数很相似，如下：

$$L(w)=L_{\hat{P}}(P_w)=\log \prod _{x,y}{P}_w(y\mid x{)}^{\tilde{P}(x,y)}=\sum _{x,y}\tilde{P}(x,y)\log P_w(y\mid x)$$

对数似然函数$L(w)$

$$L(w)=\sum _{j=1}^N\sum _{k=1}^K{w}_k{f}_k(y_j,x_j)-\sum _{j=1}^N\log Z_w(x_j)$$

数据$(x,y)$ 中出现的特征总数$T(x,y)$ ：

$$T(x,y)=\sum _k{f}_k(y,x)=\sum _{k=1}^K\sum _{i=1}^{n+1}{f}_k(y_{i-1},y_i,x)$$

输入：特征函数$t_1,t_2,\cdots ,t_{K_1}$和$s_1,s_2,\cdots ,s_{K_2}$ ；经验分布$\hat{P}(x,y)$

输出：模型参数$\hat{w}$，模型$P_{\hat{w}}$

步骤：

1 赋初值 $w_k=0$

2 对所有$k$，求解方程，解为${\delta }_k$

$$\begin{array}{rl}& \sum _{x,y}\hat{P}(x)P(y\mid x)\sum _{i=1}^{n+1}{t}_k(y_{i-1},y_i,x,i)\exp ({\delta }_{k}T(x,y))=E_{\hat{p}}[t_k],k=1,2,\cdots ,K_1\mathrm{时}\\ & \sum _{x,y}\hat{P}(x)P(y\mid x)\sum _{i=1}^{n+1}{s}_l(y_{i-1},y_i,x,i)\exp ({\delta }_{k}T(x,y))=E_{\hat{p}}[s_l],k=K_1+l,l=1,2,\cdots ,K_2\mathrm{时}\end{array}$$

3 更新$w_k+{\delta }_k\to w_k$ ，如果还有$w_k$未收敛，则继续2

算法S

对于不同的数据$(x,y)$的特征出现次数$T(x,y)$ 可能不同，可以选取一个尽量大的数$S$作为特征总数，使得所有松弛特征$s(x,y)\ge 0$ ：

$$s(x,y)=S-\sum _{i=1}^{n+1}\sum _{k=1}^K{f}_k(y_{i-1},y_i,x,i)$$

所以可以直接解得${\delta }_k$ ，当然$f_k$ 要分为$t_k$和$s_k$，对应的期望值计算也不一样。具体见书上。

$${\delta }_k=\frac{1}{S}\log \frac{E_{\hat{P}}[f_k]}{E_P[f_k]}$$

算法T

算法S中$S$会选择很大，导致每一步的迭代增量会加大，算法收敛会变慢，算法T重新选择一个特征总数 T(x)

$$T(x)=\underset{y}{max}T(x,y)$$

使用前后向递推公式，可以算得$T(x)=t$ 。

对于$k\in [1,K_1]$的$t_k$关于经验分布的期望：

$$E_{\hat{P}}[t_k]=\sum _{t=0}^{T_{max}}{a}_{k,t}{\beta }_k^t$$

其中，$a_{k,t}$是$t_k$的期待值， ${\delta }_k=\log {\beta }_k$

对于$k\in [1+K_1,K]$的$s_k$关于经验分布的期望：

$$E_{\hat{P}}[s_k]=\sum _{t=0}^{T_{max}}{b}_{k,t}{\gamma }_k^t$$

其中${\gamma }_k^t$是特征$s_k$的期望值，${\delta }_k=\log {\gamma }_k$。当然，求根也可以使用牛顿法去求解。

拟牛顿法

预测算法

预测问题

给定条件随机场$P(Y\mid X)$和输入序列$x$，求条件概率最大的输出序列（标记序列）$y^{\ast }$，即对观测序列进行标注。

$$\begin{array}{rl}{y}^{\ast }& =\arg \underset{y}{max}{P}_w(y\mid x)=\arg \underset{y}{max}\frac{\exp (w\cdot F(y,x))}{Z_w(x)}\\ & =\arg \underset{y}{max}(w\cdot F(y,x))\end{array}$$

其中路径$y$表示标记序列，下面是参数说明

$$\begin{array}{rl}& w=(w_1,w_2,\cdots ,w_k{)}^T\\ & F(y,x)=(f_1(y,x),\cdots ,f_K(y,x){)}^T,w=(w_1,\cdots ,w_K{)}^T\\ & f_k(y,x)=\sum _{i=1}^n{f}_k(y_{i-1},y_i,x,i)\\ & F_i(y_{i-1},y_i,x)={(f_1(y_{i-1},y_i,x,i),f_2(y_{i-1},y_i,x,i),\cdots ,f_k(y_{i-1},y_i,x,i))}^T\end{array}$$

所以，为了求解最优路径，只需计算非规范化概率，即转换为下面的问题：

$$\underset{y}{max}\sum _{i=1}^{n}w\cdot F_i(y_{i-1},y_i,x)$$

维特比算法

HMM的维特比算法。

维特比变量${\delta }_i(l)$，到达位置$i$， 标记为$l\in [1,m]$ 的概率

$${\delta }_i(l)=\underset{1\le j\le m}{max}\{{\delta }_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)\},j=1,2,\cdots ,m$$

记忆路径${\psi }_i(l)=a$ 当前时刻$t$标记为l, $t-1$时刻标记为a

$${\psi }_i(l)==\arg \underset{1\le j\le m}{max}\{{\delta }_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)\}$$

算法主体

输入：特征向量$F(y,x)$和权值向量$\mathbf{w}$，观测向量$x=(x_1,x_2,\cdots .x_n)$

输出：最优路径$y^{\ast }=(y_1^{\ast },y_2^{\ast },\cdots ,y_n^{\ast })$

步骤如下

初始化

$${\delta }_1(j)=w\cdot F_1(y_0=start,y_1=j,x),j=1,\cdots ,m$$

递推

$$\begin{array}{rl}& {\delta }_i(l)=\underset{1\le j\le m}{max}\{{\delta }_{i-1}(j)+w\cdot F_i(y_{i-1}=j,y_i=l,x)\},j=1,2,\cdots ,m\\ & {\psi }_i(l)=\arg \underset{1\le j\le m}{max}{\delta }_i(j),\text{即上式的参数j}\end{array}$$

终止

$$\begin{array}{rl}& \underset{y}{max}(w\cdot F(y,x))=\underset{1\le j\le m}{max}{\delta }_n(j)\\ & y_n^{\ast }=\arg \underset{1\le j\le m}{max}{\delta }_n(j)\end{array}$$

返回路径

$$y_i^{\ast }={\psi }_{i+1}(y_{i+1}^{\ast }),i=n-1,n-2,\cdots ,1$$

求得最优路径$y^{\ast }=(y_1^{\ast },y_2^{\ast },\cdots ,y_n^{\ast })$