吴恩达线性回归、逻辑回归、梯度下降笔记

线性回归

有$m$个样本$(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots ,(x^{(m)},y^{(m)})$，假设函数有2个参数${\theta }_0,{\theta }_1$，形式如下：

$$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$$

代价函数

代价函数

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$$

目标是要找到合适的参数，去最小化代价函数$minJ({\theta }_0,{\theta }_1)$。

假设${\theta }_0=0$，去描绘出$J({\theta }_1)$和${\theta }_1$的关系，如下面右图所示。

假设有3个样本$(1,1),(2,2),(3,3)$，图中选取了3个${\theta }_1=1,0.5,0$，其中$J({\theta }_1)$在${\theta }_1=1$时最小。

那么回到最初的两个参数$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$，如何去找$minJ({\theta }_0,{\theta }_1)$呢？这里绘制一个等高图去表示代价函数，如下面右图所示，其中中间点是代价最小的。

梯度下降

基础说明

上文已经定义了代价函数$J({\theta }_0,{\theta }_1)$，这里要使用梯度下降算法去最小化$J({\theta }_0,{\theta }_1)$，自动寻找出最合适的$\theta$。梯度下降算法应用很广泛，很重要。大体步骤如下：

• 设置初始值${\theta }_0,{\theta }_1$
• 不停改变${\theta }_0,{\theta }_1$去减少$J({\theta }_0,{\theta }_1)$

当然选择不同的初始值，可能会得到不同的结果，得到局部最优解。

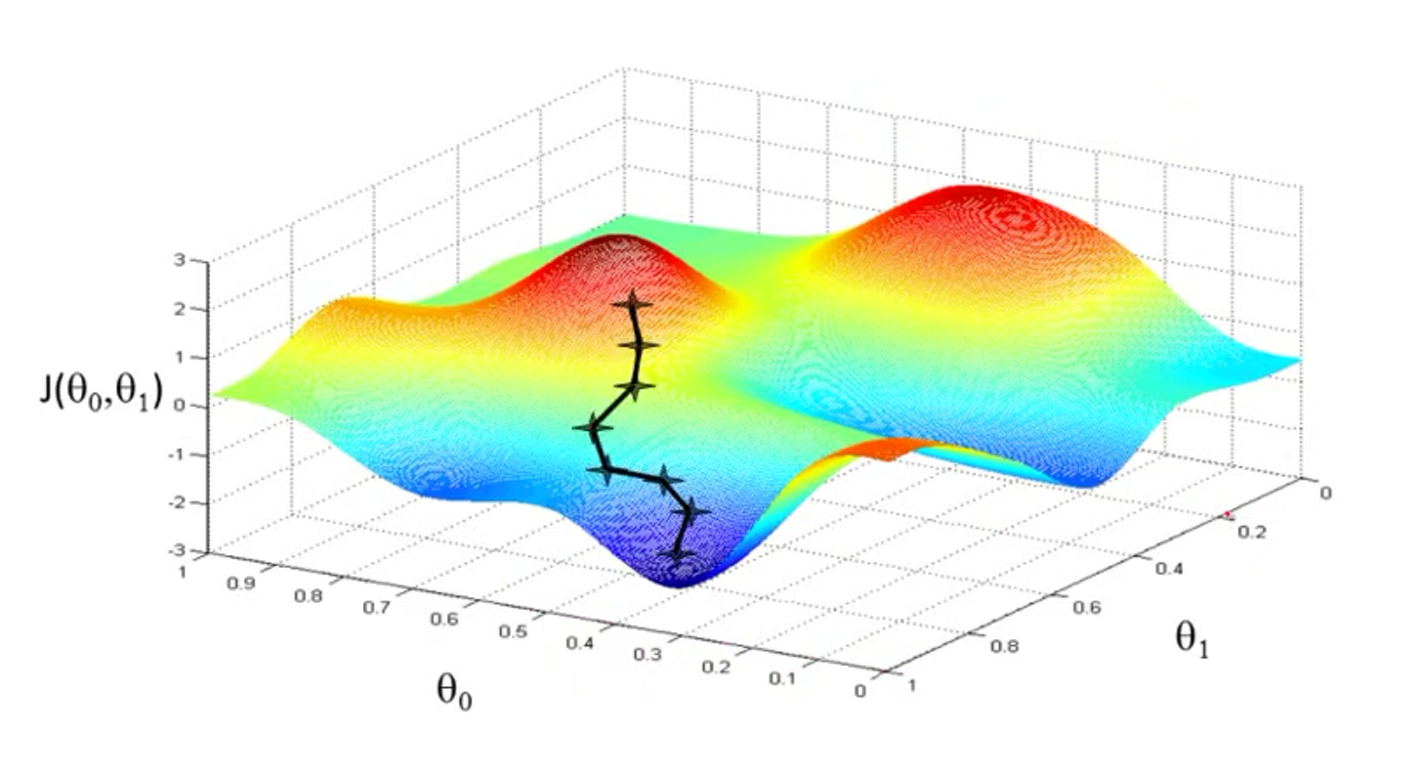
对于所有的参数${\theta }_j$进行同步更新，式子如下

$${\theta }_j={\theta }_j-\underset{\mathrm{学}\mathrm{习}\mathrm{率}\times \mathrm{偏}\mathrm{导}}{\underbrace{\alpha \cdot \frac{\partial }{{\partial }_{{\theta }_j}}J({\theta }_0,{\theta }_1)}}$$

上面公式中$\alpha$是学习率(learning rate)，是指一次迈多大的步子，一次更新的幅度大小。

例如上面的两个参数，对于一次同步更新(梯度下降)

$$t_0={\theta }_0-\alpha \frac{\partial }{{\partial }_{{\theta }_0}}J({\theta }_0,{\theta }_1),t_1={\theta }_1-\alpha \frac{\partial }{{\partial }_{{\theta }_1}}J({\theta }_0,{\theta }_1)\to {\theta }_0=t_0,{\theta }_1=t_1$$

也有异步更新(一般指别的算法)

$$t_0={\theta }_0-\alpha \frac{\partial }{{\partial }_{{\theta }_0}}J({\theta }_0,{\theta }_1),{\theta }_0=t_0\to t_1={\theta }_1-\alpha \frac{\partial }{{\partial }_{{\theta }_1}}J({\theta }_0,{\theta }_1),{\theta }_1=t_1$$

偏导和学习率

这里先看一个参数的例子，即$J({\theta }_1)$。${\theta }_1={\theta }_1-\alpha \frac{d}{dx}J({\theta }_1)$。当$\theta$从左右靠近中间值，导数值(偏导/斜率)分别是负、正，所以从左右两端都会靠近中间值。

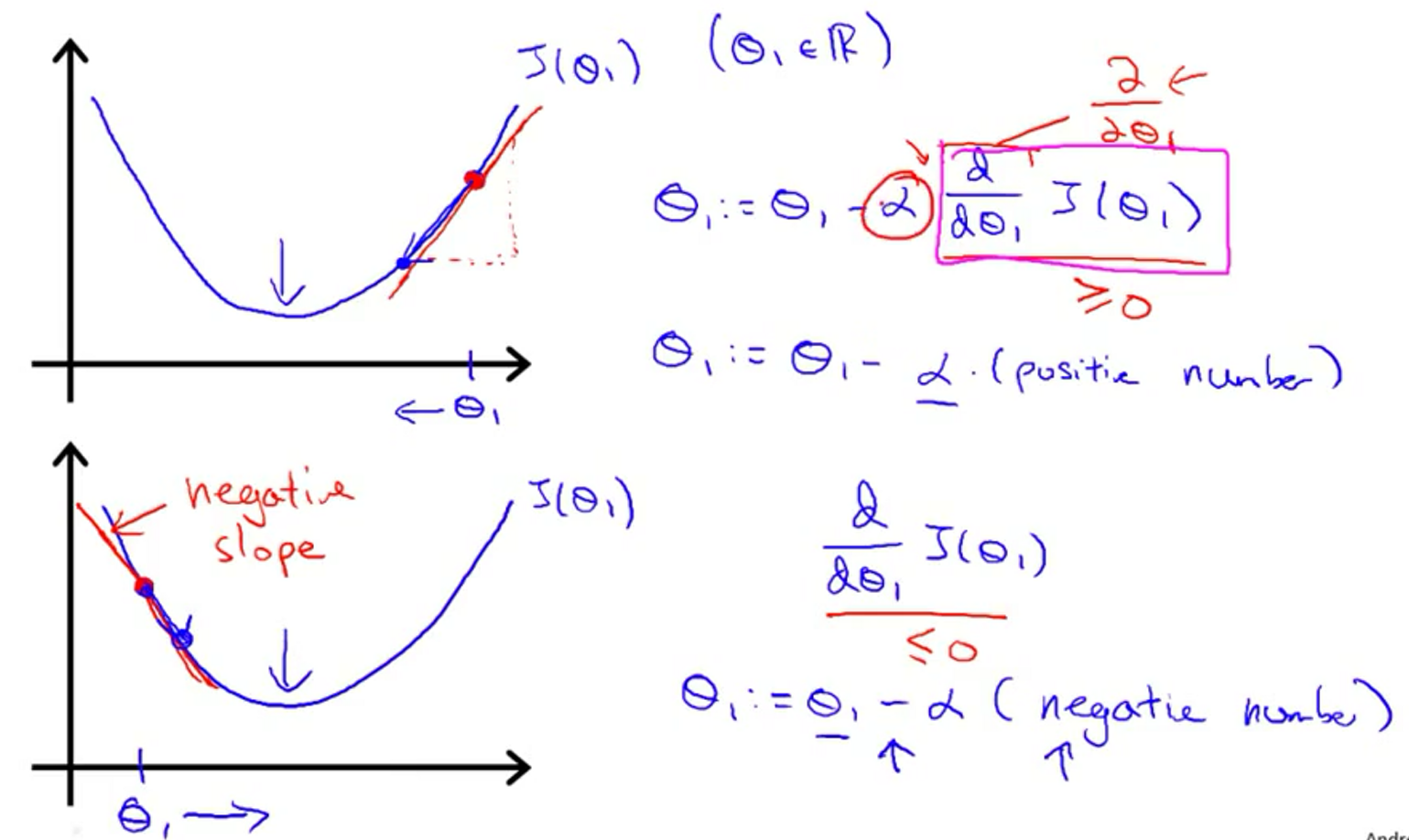
当学习率$\alpha$太小，梯度下降会很缓慢；$\alpha$太大，可能会错过最低点，导致无法收敛。

当已经处于局部最优的时候，导数为0，并不会改变参数的值，如下图

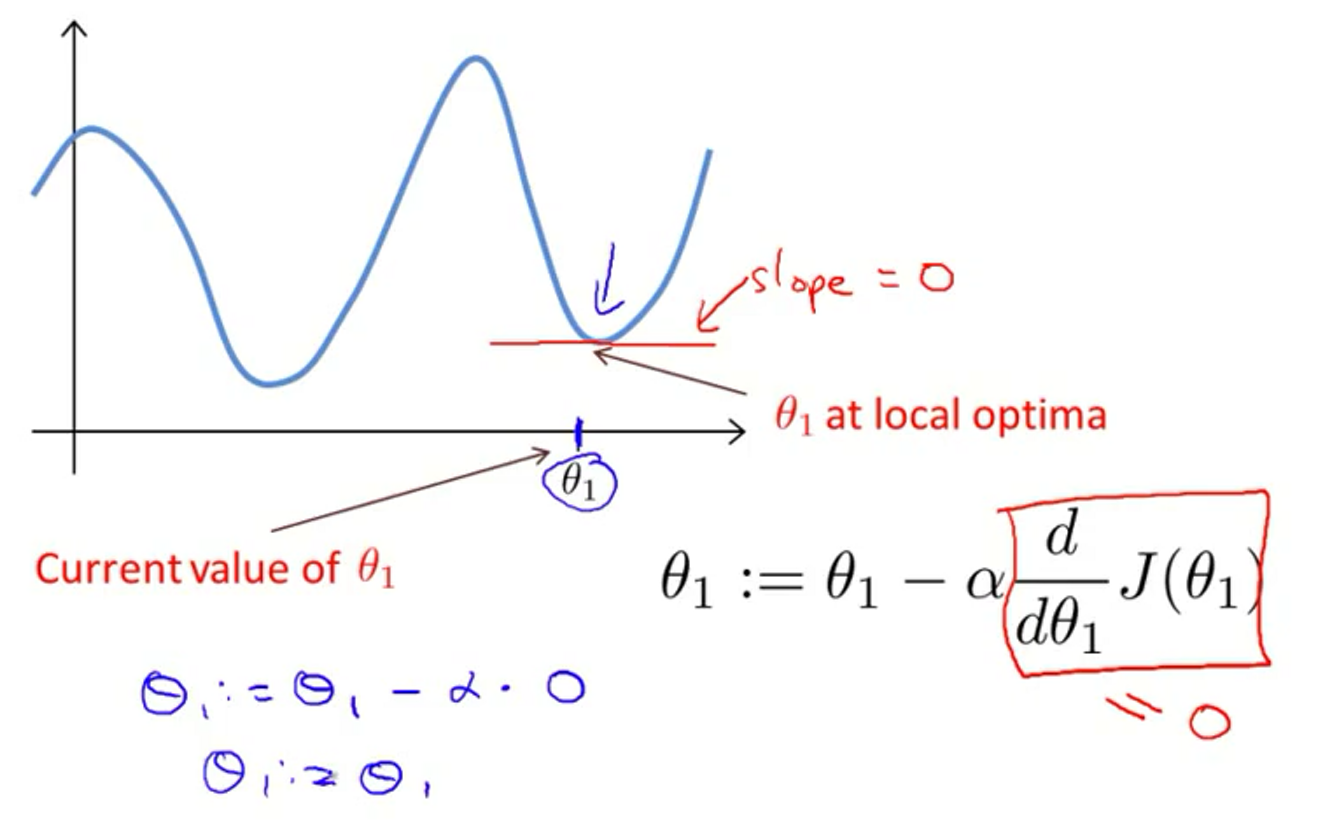
当逐渐靠近局部最优的时候，梯度下降会自动采取小步子到达局部最优点。是因为越接近，导数会越来越小。

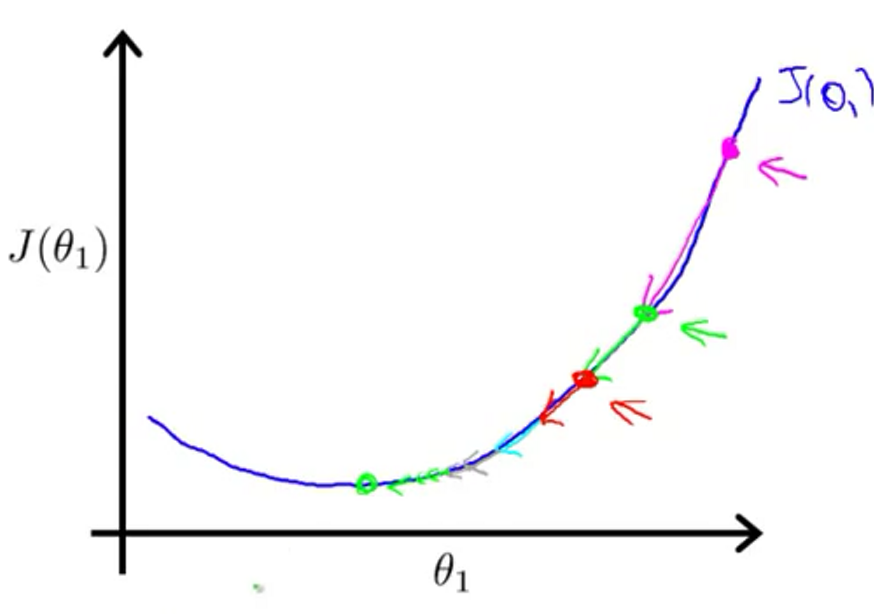
在线性回归上使用梯度下降

代价函数

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2=\frac{1}{2m}\sum _{i=1}^m({\theta }_0+{\theta }_1{x}^{(i)}-y^{(i)}{)}^2$$

分别对${\theta }_0$和${\theta }_1$求偏导有

$$\frac{\partial }{{\partial }_{{\theta }_0}}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}),\frac{\partial }{{\partial }_{{\theta }_1}}J({\theta }_0,{\theta }_1)=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^{(i)}$$

那么使用梯度下降对${\theta }_0\mathrm{和}{\theta }_1$进行更新，如下

$${\theta }_0={\theta }_0-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}),{\theta }_1={\theta }_1-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x^{(i)}$$

当前代价函数实际上是一个凸函数，如下图所示。它只有全局最优，没有局部最优。

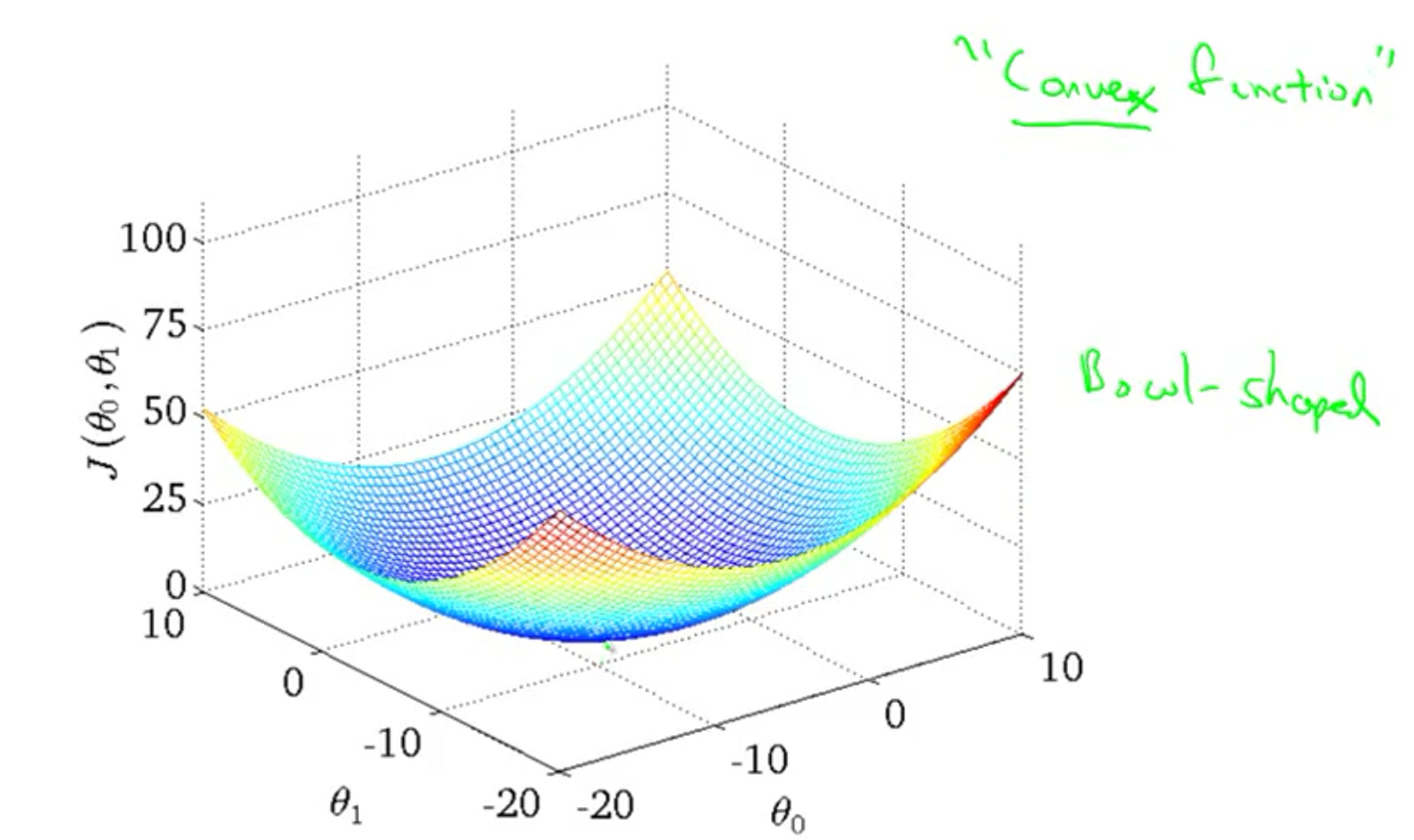
通过不断地改变参数减小代价函数$J({\theta }_0,{\theta }_1)$，逼近最优解，最终会得到一组比较好的参数，正好拟合了我们的训练数据，就可以进行新的值预测。

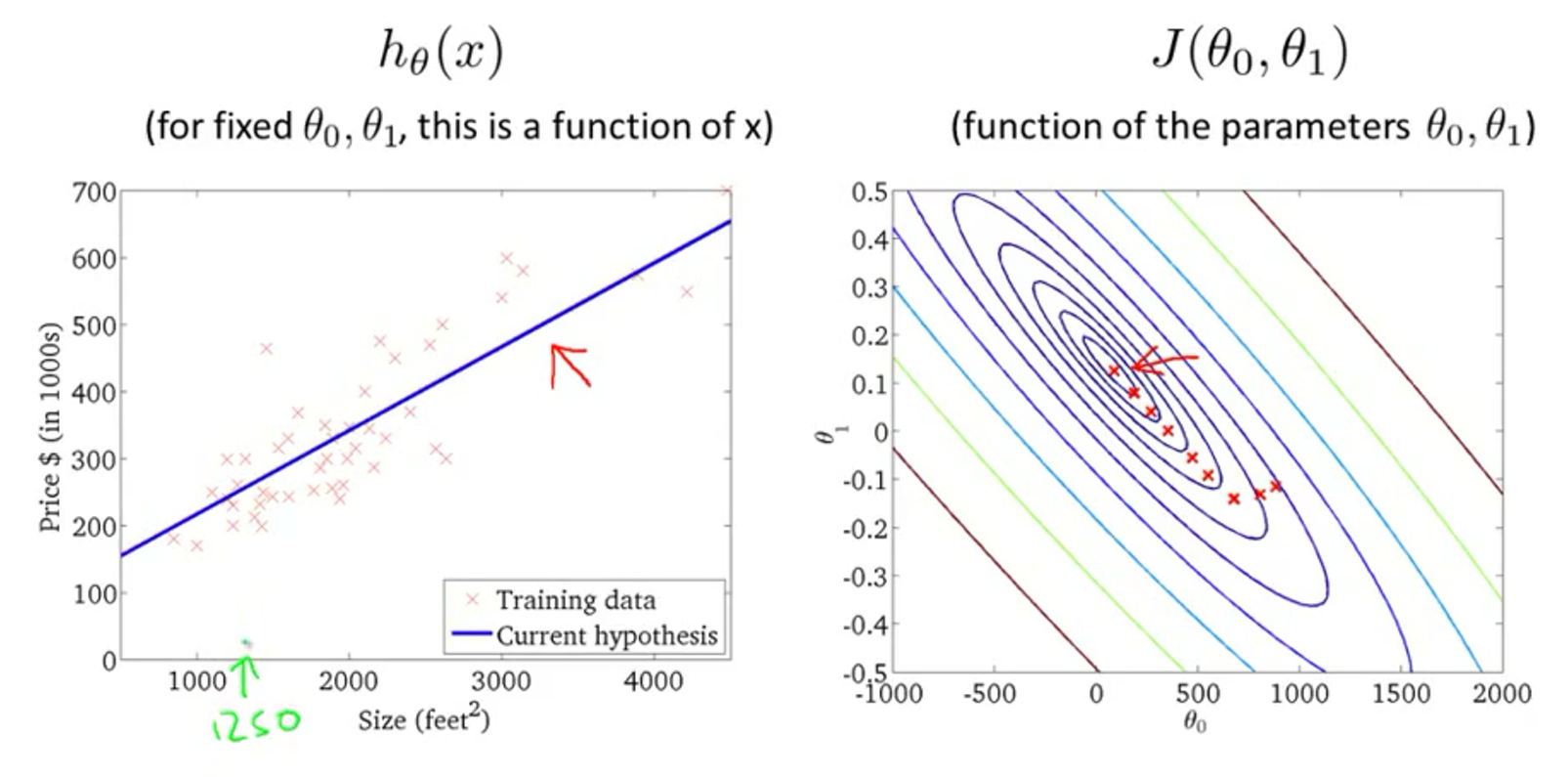
梯度下降技巧

特征缩放

不同的特征的单位的数值变化范围不一样，比如$x_1\in (0,2000),x_2\in (1,5)$，这样会导致代价函数$J(\theta )$特别的偏，椭圆。这样来进行梯度下降会特别的慢，会来回震荡。

所以特征缩放是把所有的特征缩放到相同的规模上。得到的$J(\theta )$就会比较圆，梯度下降能很快地找到一条通往全局最小的捷径。

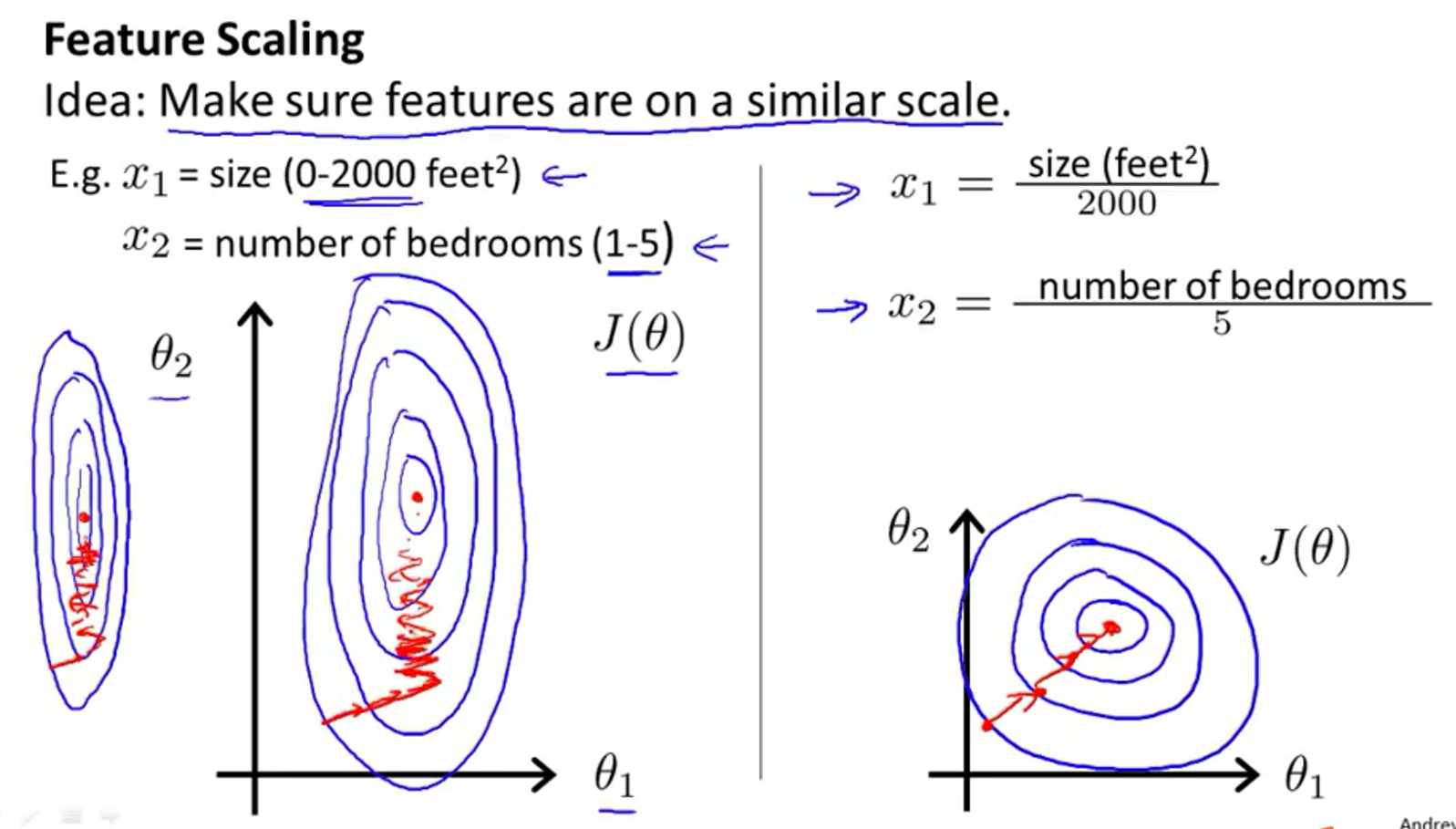
特征缩放的数据规模不能太小或者太大，如下面可以的规模是

$$[-1,1],[0,3],[-2,0.5],[-3,3],[-\frac{1}{3},\frac{1}{3}]\mathrm{都}\mathrm{是}\mathrm{可}\mathrm{以}\mathrm{的}。\mathrm{而}[-100,100],[-0.0001,0.0001]\mathrm{是}\mathrm{不}\mathrm{可}\mathrm{以}\mathrm{的}$$

有一些常见的缩放方法

• $x_i=\frac{x_i-\mu }{max-min}$, $x_i=\frac{x_i-\mu }{s}$，其中$\mu$是均值，$s$是标准差
• $x_i=\frac{x_i-min}{max-min}$
• $x_i=\frac{x_i}{max}$

学习率的选择

当梯度下降正确运行的时候，每一次迭代$J(\theta )$都会减少，但是减少到什么时候合适呢？当然最好的办法就是画图去观察，当然也可以设定减小的最小值来判断。下图中， 迭代次数到达400的时候就已经收敛。不同的算法，收敛次数不一样。

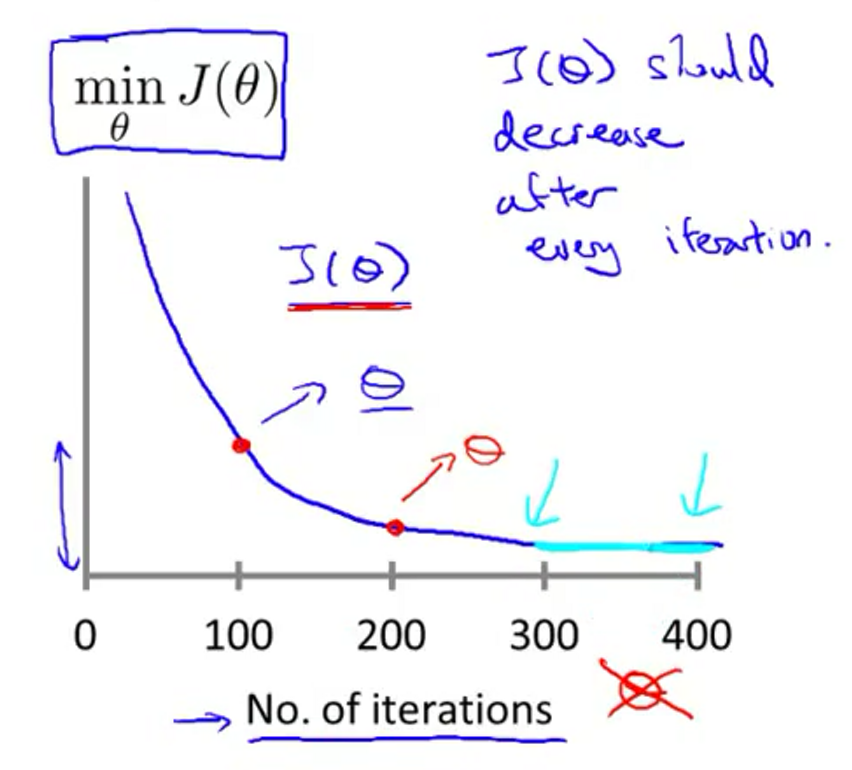
当图像呈现如下的形状，就需要使用更小的学习率。理论上讲，只要使用足够小的学习率，$J(\theta )$每次都会减少。但是太小的话，梯度下降会太慢，难以收敛。

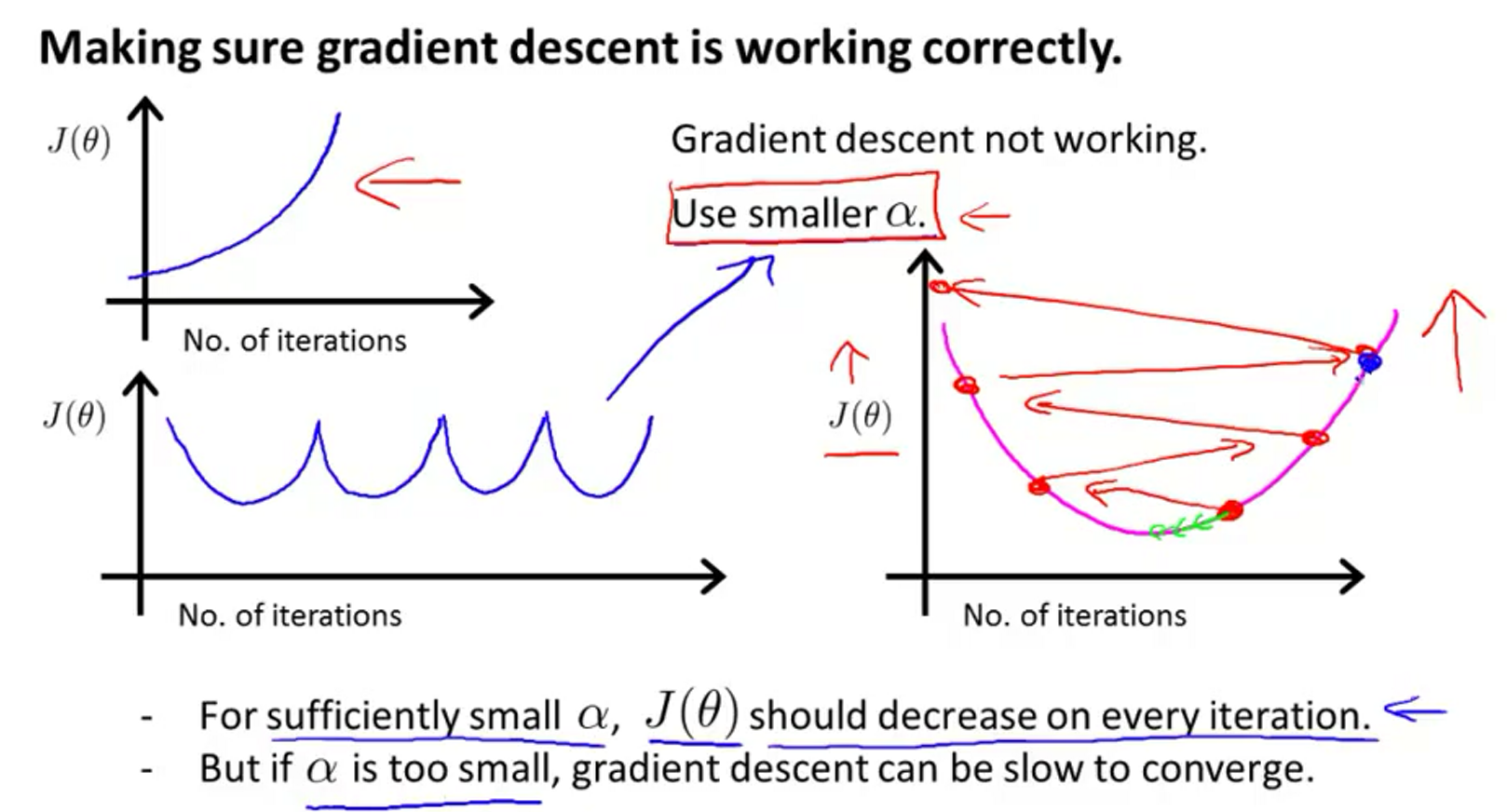
学习率总结

• 学习率太小，慢收敛
• 学习率太大，$J(\theta )$可能不会每次迭代都减小，甚至不会收敛
• 这样去选择学习率调试： $\dots ,0.001,0.003,0.01,0.03,0.1,0.3,1,\dots$

多变量线性回归

数据有$n$个特征，如$x^{(i)}=(1,x_1,x_2,\cdots ,x_n)$，其中$x_0=1$。则假设函数有$n+1$个参数，形式如下

$$h_{\theta }(x)={\theta }^{T}x={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\cdots +{\theta }_n{x}_n$$

代价函数

$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$$

梯度下降，更新每个参数${\theta }_j$

$${\theta }_j={\theta }_j-\alpha \cdot \frac{\partial J(\theta )}{{\partial }_{{\theta }_j}}={\theta }_j-\alpha \cdot \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_j^{(i)}$$

多项式回归

有时候，线性回归并不能很好地拟合数据，所以我们需要曲线来适应我们的数据。比如一个二次方模型

$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2^2$$

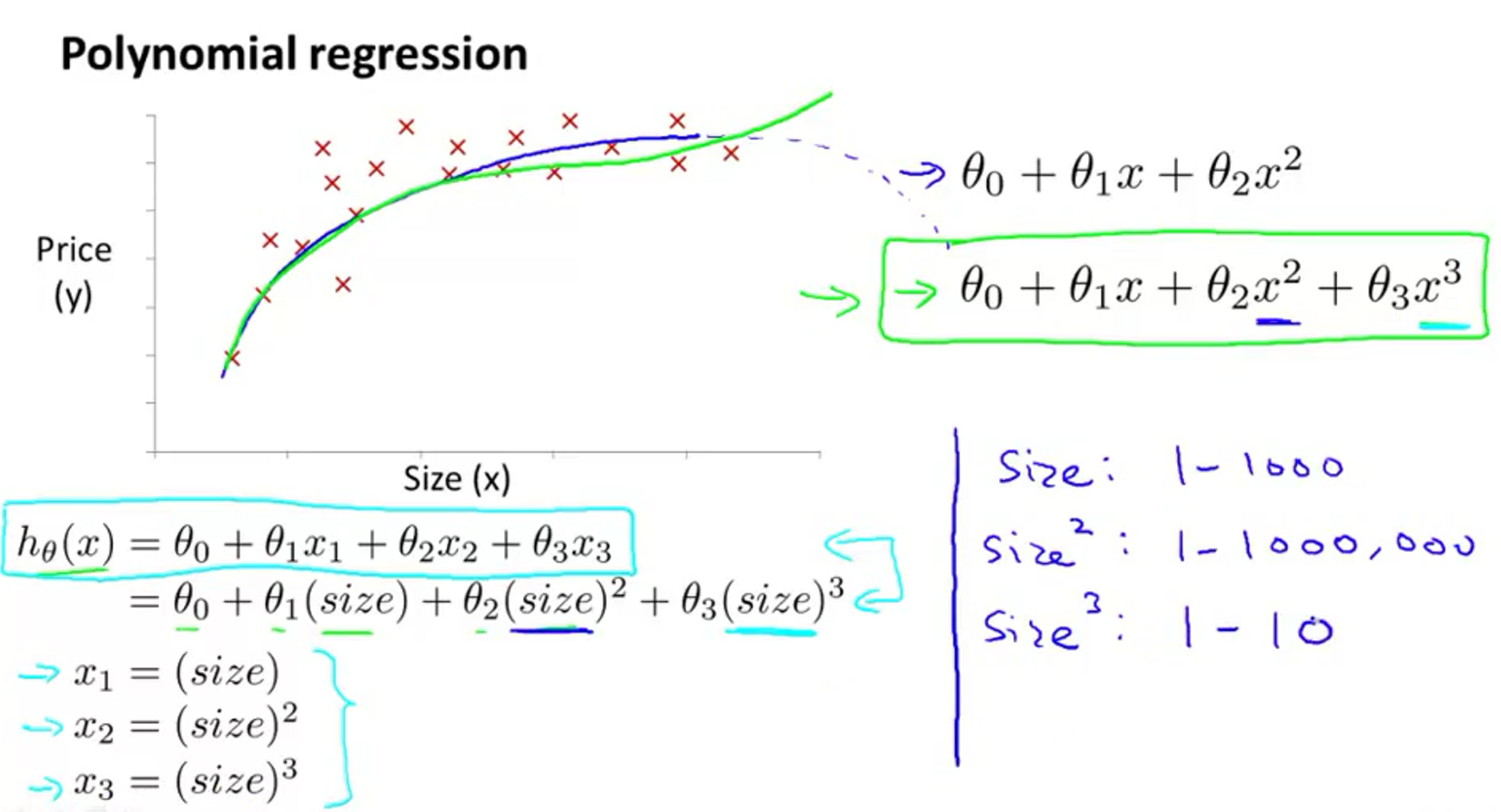
当然可以用$x_2=x_2^2,x_3=x_3^3$来转化为多变量线性回归。如果使用多项式回归，那么在梯度下降之前，就必须要使用特征缩放。

正规方程

对于一些线性回归问题，使用正规方程方法求解参数$\theta$，比用梯度下降更好些。代价函数如下

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$$

正规方程的思想是函数$J(\theta )$对每个${\theta }_j$求偏导令其等于0，就能得到所有的参数。即$\frac{\partial J}{\partial {\theta }_j}=0$。

那么设$X_{m\times (n+1)}$为数据矩阵（其中包括$x_0=1$），$y$为标签向量。则通过如下方程可以求得$\theta$

$$\theta =(X^{T}X{)}^{-1}{X}^{T}y$$

正规方程和梯度下降的比较

梯度下降	正规方程
需要特征缩放	不需要特征缩放
需要选择学习率$\alpha$	不虚选择学习率
需要多次迭代计算	一次运算出结果
特征数量$n$很大时，依然适用	$n$太大，求矩阵逆运算代价太大，复杂度为$O(n^3)$。$n\le 10000$可以接受
适用于各种模型	只适用于线性模型，不适合逻辑回归和其他模型

逻辑回归

线性回归有2个不好的问题：直线难以拟合很多数据；数据标签一般是$0,1$，但是$h_{\theta }(x)$却可能远大于1或者远小于0。如下图。

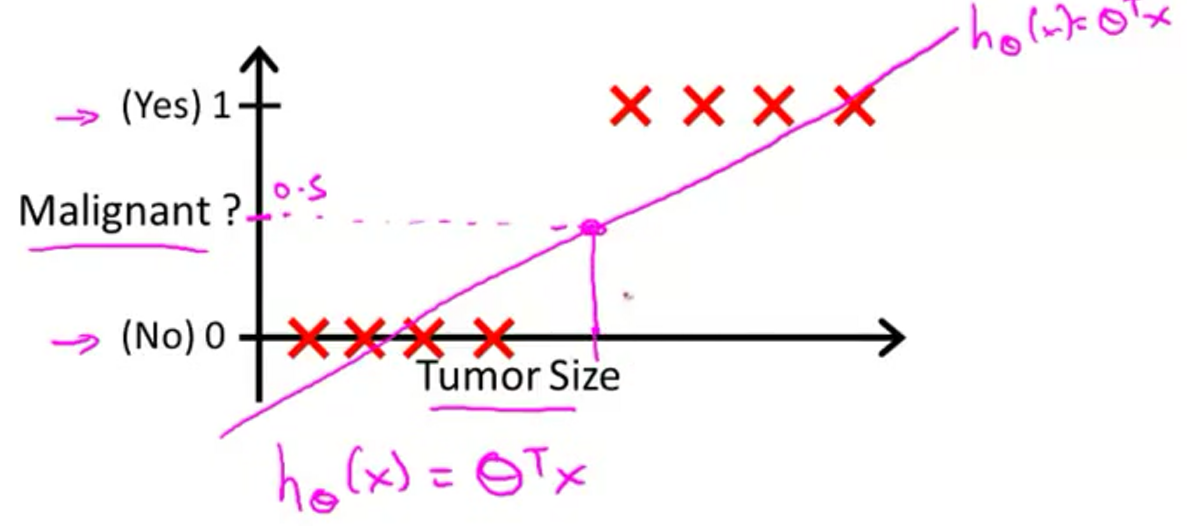
基本模型

逻辑回归是一种分类算法，使得输出预测值永远在0和1之间，是使用最广泛的分类算法。模型如下

$$h_{\theta }(x)=g({\theta }^{T}x),g(z)=\frac{1}{1+e^{-z}}$$

$g(z)$的图像如下，也称作Sigmoid函数或者Logistic函数，是S形函数。

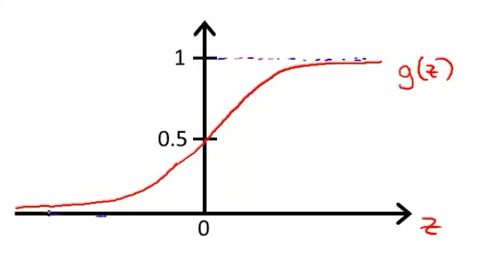
将上面的公式整理后得到逻辑回归的模型

$$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}},\mathrm{其}\mathrm{中}0\le h_{\theta }(x)\le 1$$

模型的意义是给出分类为1的概率，即$h_{\theta }(x)=P(y=1\mid x;\theta )$。例如$h_{\theta }(x)=0.7$，则分类为1的概率是0.7，分类为0的概率是$1-0.7=0.3$。

$$x\mathrm{的}\mathrm{分}\mathrm{类}\mathrm{预}\mathrm{测},y=\{\begin{array}{ll}1,& h_{\theta }(x)\ge 0.5,\mathrm{即}{\theta }^{T}x\ge 0\\ 0,& h_{\theta }(x)<0.5,\mathrm{即}{\theta }^{T}x<0\end{array}$$

逻辑回归就是要学到合适的$\theta$，使得正例的特征远大于0，负例的特征远小于0。

决策边界

线性边界

假设我们有一个模型$h_{\theta }(x)=g({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2)$，已经确定参数$\theta =(-3,1,1)$，即模型$h_{\theta }(x)=g(-3+x_1+x_2)$，数据和模型如下图所示

由上可知，分类结果如下

$$y=\{\begin{array}{ll}1,& x_1+x_2\ge 3\\ 0,& x_1+x_2<3\end{array}$$

那么直线$x_1+x_2=3$就称作模型的决策边界，将预测为1的区域和预测为0的区域分隔开来。gg

非线性边界

先看下面的数据

使用这样的模型去拟合数据

$$h_{\theta }(x)=g({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2),\theta =(-1,0,0,1,1),\mathrm{即}{h}_{\theta }(x)=g(-1+x_1^2+x_2^2)$$

对于更复杂的情况，可以用更复杂的模型去拟合，如$x_1{x}_2,x_1{x}_2^2$等

代价函数和梯度下降

我们知道线性回归中的代价函数是$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m{(h_{\theta }(x^{(i)})-y^{(i)})}^2$，但是由于逻辑回归的模型是$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$，所以代价函数关于$\theta$的图像就是一个非凸函数，容易达到局部收敛，如下图左边所示。而右边，则是一个凸函数，有全局最小值。

代价函数

逻辑回归的代价函数

$$\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}({\mathrm{h}}_{\theta }(\mathrm{x}),\mathrm{y})=\{\begin{array}{ll}-\log (h_{\theta }(x)),& y=1\\ -\log (1-h_{\theta }(x)),& y=0\end{array}$$

当实际上$y=1$时，若预测为0，则代价会无穷大。当实际上$y=0$时，若预测为1，则代价会无穷大。

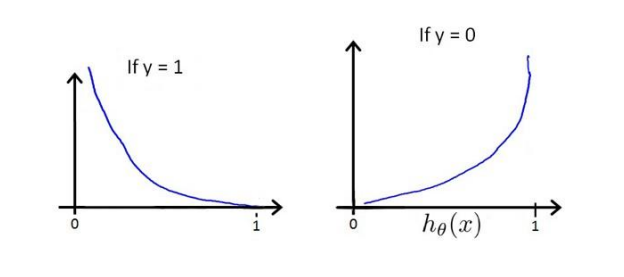
整理代价函数如下

$$\mathrm{C}\mathrm{o}\mathrm{s}\mathrm{t}({\mathrm{h}}_{\theta }(\mathrm{x}),\mathrm{y})=-\mathrm{y}\cdot \log ({\mathrm{h}}_{\theta }(\mathrm{x}))-(1-\mathrm{y})\cdot \log (1-{\mathrm{h}}_{\theta }(\mathrm{x}))$$

得到所有的$J(\theta )$

$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log h_{\theta }(x^{(i)})+(1-y^{(i)})\log (1-h_{\theta }(x^{(i)})))$$

梯度下降

逻辑回归的假设函数估计$y=1$的概率 $h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$。

代价函数$J(\theta )$，求参数$\theta$去$\underset{\theta }{min}J(\theta )$

对每个参数${\theta }_j$，依次更新参数

$${\theta }_j={\theta }_j-\alpha \cdot \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})\cdot x_j^{(i)}$$

逻辑回归虽然梯度下降的式子和线性回归看起来一样，但是实际上$h_{\theta }(x)$和$J(\theta )$都不一样，所以是不一样的。