所有排序算法的介绍、实现和比较，值得一看

插入排序

直接插入

前面的已经有序，把后面的插入到前面有序的元素中。

步骤

• 找到待插入位置
• 给插入元素腾出空间，边比较边移动

如对4 5 1 2 6 3

# 5插入4
4 5   1 2 6 3
# 1插入 4 5
1 4 5   2 6 3
# 2插入 1 4 5
1 2 4 5   6 3
# 6插入 1 2 4 5
1 2 4 5 6   3
# 3插入到前面
1 2 3 4 5 6

关键代码

/**
 * 直接插入排序，先比较找位置，再移动
 **/ 
void insert_sort(int a[], int n) {
    for (int i = 1; i < n; i++) {
        // 最大，追加在末尾即可
        if (a[i] > a[i-1]) {
            continue;
        }

        // 找到待插入的位置
        int k = -1;
        for (int j = 0; j < i; j++) {
            if (a[i] < a[j]) {
                k = j;
                break;
            }
        }
        int t = a[i];
        // 先挪动元素，向后移动
        for (int j = i; j > k; j--) {
            a[j] = a[j-1];
        }
        a[k] = t;
    }
}

/**
 * 直接插入排序，边比较边移动
 **/
void insert_sort2(int a[], int n) {
    for (int i = 1; i < n; i++) {
        if (a[i] < a[i-1]) {
            int t = a[i];
            int j = i - 1;
            while (a[j] > t && j >= 0) {
                a[j+1] = a[j];
                j--;
            }
            a[j+1] = t;
        }
    }
}

总结分析

名称	时间	最好	最差	空间	稳定	适用性
直接插入	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	是	顺序存储和链式存储的线性表

折半插入

先折半查找出位置，再统一的移动。 若m为1个数字，则$a[i]>a[m]$，该插入位置为$l=m+1$。

仅仅减少了元素的比较次数，元素的移动次数依然没有改变。时间复杂度仍然为$\mathrm{O}(n)$。

关键代码

/**
 * 插入排序，折半查找出位置，再统一移动
 **/ 
void insert_sort_bisearch(int a[], int n) {
    for (int i = 1; i < n; i++) {
        if (a[i] > a[i-1]) {
            continue;
        }
        // 折半查找，a[i]要插入的位置为l
        int l = 0, r = i - 1;
        while (l <= r) {
            int m = (l + r) / 2;
            if (a[i] > a[m]) {
                // 查找右边
                l = m + 1;
            } else if (a[i] < a[m]){
                // 查找左边
                r = m - 1;
            } else {
                l = m + 1;
                break;
            }
        }
        int t = a[i];
        for (int j = i; j > l; j--) {
            a[j] = a[j-1];
        }
        a[l] = t;
    }
}

希尔排序

希尔排序又称为缩小增量排序， 把整个列表，分成多个$\mathrm{L}[\mathrm{i},\mathrm{i}+\mathrm{d},\mathrm{i}+2\mathrm{d},\cdots ,\mathrm{i}+\mathrm{k}\mathrm{d}]$这样的列表，每个进行直接插入排序。每一轮不断缩小d的值，直到全部有序。

实际例子 4 5 1 2 6 3

# d = 3
4 _ _ 2 _ _
_ 5 _ _ 6 _
_ _ 1 _ _ 3
# 化为3个列表，分别进行直接插入排序，得到
2 5 1 4 6 3

# d = 2
2 _ 1 _ 6 _
_ 5 _ 4 _ 3
# 排序，得到
1 3 2 4 6 5

# d = 1
1 3 2 4 6 5
# 直接插入排序，得到
1 2 3 4 5 6

关键代码

/*
 * 希尔排序，按照步长，去划分为多个组。对这些组分别进行插入排序
 */
void shell_sort(vector<int>& a) {
    // 步长gap==组的个数
    for (int gap = a.size() / 2; gap > 0; gap = gap / 2) {
        // 对各个组进行排序
        for (int i = 0; i < gap; i++) {
            group_sort(a, i, gap);
        }
    }
}

/*
 * 对希尔排序中的单个组进行排序，直接插入
 * Args:
 *      a -- 数组
 *      start -- 该组的起始地址
 *      gap -- 组的步长，也是组的个数
 */
void group_sort(vector<int> &a, int start, int gap) {
    for (int i = start + gap; i < a.size(); i += gap) {
        if (a[i] < a[i - gap]) {
            int t = a[i];
            int j = i - gap;
            // 从后向前比较，边比较，边移动
            while (a[j] > t && j >= start) {
                a[j + gap] = a[j];
                j -= gap;
            }
            a[j + gap] = t;
        }
    }
}

总结分析

最好的增量$d_1=\frac{n}{2},d_{i+1}=\lfloor \frac{d_i}{2}\rfloor$

名称	时间	最好	最差	空间	稳定	适用性
希尔排序				$O(1)$	不稳定	线性存储的线性表

交换排序

冒泡排序

执行n-1轮，每一轮把$a[0,\dots ,i]$的最大的向下沉。

2 4 3 1 6 5
# 第一趟
2 4 _ _ _ _
2 3 4 _ _ _		# 4-3 to 3-4
2 3 1 4 _ _		# 4-1 to 1-4 
2 3 1 4 6 _		
2 3 1 4 5 6		# 6-5 to 5-6
# 第二趟
2 3 _ _ _  6	
2 1 3 _ _  6	# 3-1 to 1-3
2 1 3 4 _  6	
2 1 3 4 5  6
# 第三趟
1 2 _ _  5 6	# 2-1 to 1-2
1 2 3 _  5 6
1 2 3 4  5 6

关键代码

void bubble_sort1(int* a, int n) {
    for (int i = n-1; i > 0; i--) {
        // 每一轮把a[0,...,i]中最大的向下沉
        for (int j = 0; j < i; j++) {
            if (a[j] > a[j+1]) {
                int t = a[j];
                a[j] = a[j+1];
                a[j+1] = t;
            }
        }
    } 
}

// 若当前轮，已经没有发生交换，说明已经全部有序
void bubble_sort2(int* a, int n) {
    int swapped = 0;
    for (int i = n - 1; i > 0; i--) {
        swapped = 0;
        for (int j = 0; j < i; j++) {
            if (a[j] > a[j+1]) {
                int t = a[j];
                a[j] = a[j+1];
                a[j+1] = t;
                swapped = 1;
            }
        }
        if (swapped = 0) {
            break;
        }
    }
}

总结分析

名称	时间	最好	最差	空间	稳定	备注
冒泡排序	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	是	每一轮都有一个元素到最终位置上

快速排序

思想

把一个序列，选一个数（第一个数），进行划分。左边小于x，中间x，右边大于x。再依次递归划分左右两边。

关键代码

划分

/**
 * 划分，左边小于x，中间x，右边大于x
 * Args:
 *      a:
 *      l:
 *      r:
 * Returns:
 *      i: x=a[l]的最终所在位置
 **/
int partition(int* a, int l, int r) {
    int x = a[l];
    int i = l;
    int j = r;
    // 划分
    while (i < j) {
        // 从右到左，找到第一个小于x的a[j]，放到a[i]上
        while (a[j] >= x && j > i) {
            j--;
        }
        // 把a[j]放到左边i上
        if (j > i) {
            a[i++] = a[j];
        }
        // 从左到右，找到一个大于x的[i]
        while (a[i] <= x && i < j) {
            i++;
        }
        // 把a[i]放到右边j上
        if (i < j) {
            a[j--] = a[i];
        }
    }
    // x放在中间
    a[i] = x;
    return i;
}

递归快排

void quick_sort(int* a, int l, int r) {
    // 1. 递归终止
    if (l >= r) {
        return;
    }
    // 2. 划分，左边小于x，中间x，右边大于x
    int k = partition(a, l, r);
    // 3. 递归快排左右两边
    quick_sort(a, l, k - 1);
    quick_sort(a, k + 1, r);
}

非递归快排

void quick_sort_stack(int* a, int l, int r) {
    int i, j;
    stack<int> st;
    // 注意进栈和出栈的顺序
    st.push(r);
    st.push(l);
    while (st.empty() == false) {
      	// 每次出栈一组
        i = st.top();
        st.pop();
        j = st.top();
        st.pop();
        if (i < j) {
            int k = partition(a, i, j);
          	// 左边的
            if (k > i) {
                st.push(k - 1);
                st.push(i);
            }
          	// 右边的
            if (k < j) {
                st.push(j);
                st.push(k + 1);
            }
        }
    }
}

总结分析

第i趟完成后，最少有i个元素在最终位置。

名称	时间	最好	最差	空间	稳定	备注
快排	$O(n\log n)$	$O(n\log n)$	$O(n^2)$	$O({\log }_{2}n)$栈的深度	不稳定	基本有序或者逆序，效果最差

选择排序

简单选择

前面已经有序，从后面选择最小的与前面末尾最大的进行交换。

4  5 1 2 6 3
# 选择1与4交换
1  5 4 2 6 3
# 选择2与5交换
1 2  4 5 6 3
# 选择3与4交换
1 2 3  5 6 4
# 选择4与5交换
1 2 3 4  6 5
# 选择5与6交换
1 2 3 4 5  6

总结分析

名称	时间	最好	最差	空间	稳定	备注
简单选择	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	不稳定

关键代码

/**
 * 简单选择排序，选择后面最小的来与当前有序的最后一个（最大的）交换
 **/
void select_sort(int *a, int n) {
    for (int i = 1; i < n; i++) {
        int k = min_index(a, i, n-1);
        if (a[i-1] > a[k]) {
            swap(a, i-1, k);
        }
    }
}

堆

堆

堆是一颗完全二叉树。

有n个节点，堆的索引从0开始，节点i的

• 左孩子：$2\cdot i+1$
• 右孩子：$2\cdot i+2$
• 父亲：$\lceil \frac{i-1}{2}\rceil$
• 最后一个节点是：下标为$\lfloor n/2\rfloor -1$ 的节点的孩子，即第$\lfloor n/2\rfloor$个节点的孩子。

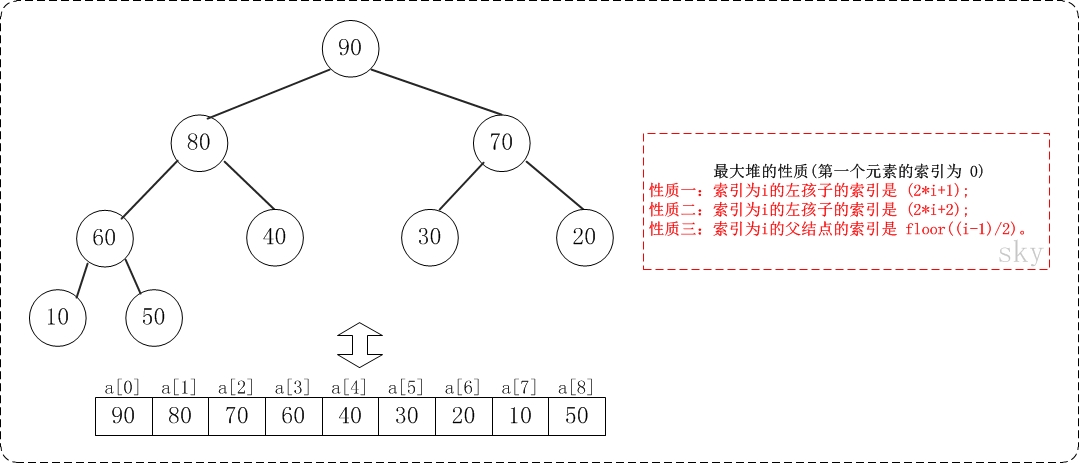
大根堆

大根堆：最大元素在根节点。小根堆：最小元素在根节点。

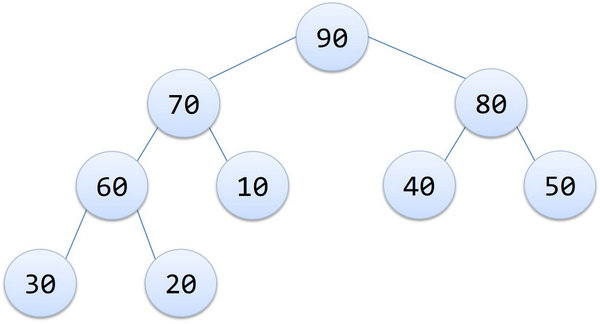
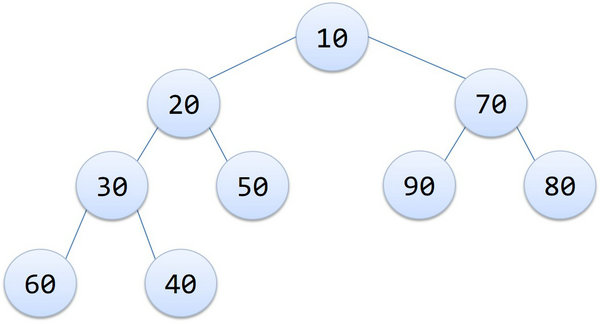
90 70 80 60 10 40 50 30 20 是一个大根堆，10 20 70 30 50 90 80 60 40 是一个小根堆，如下

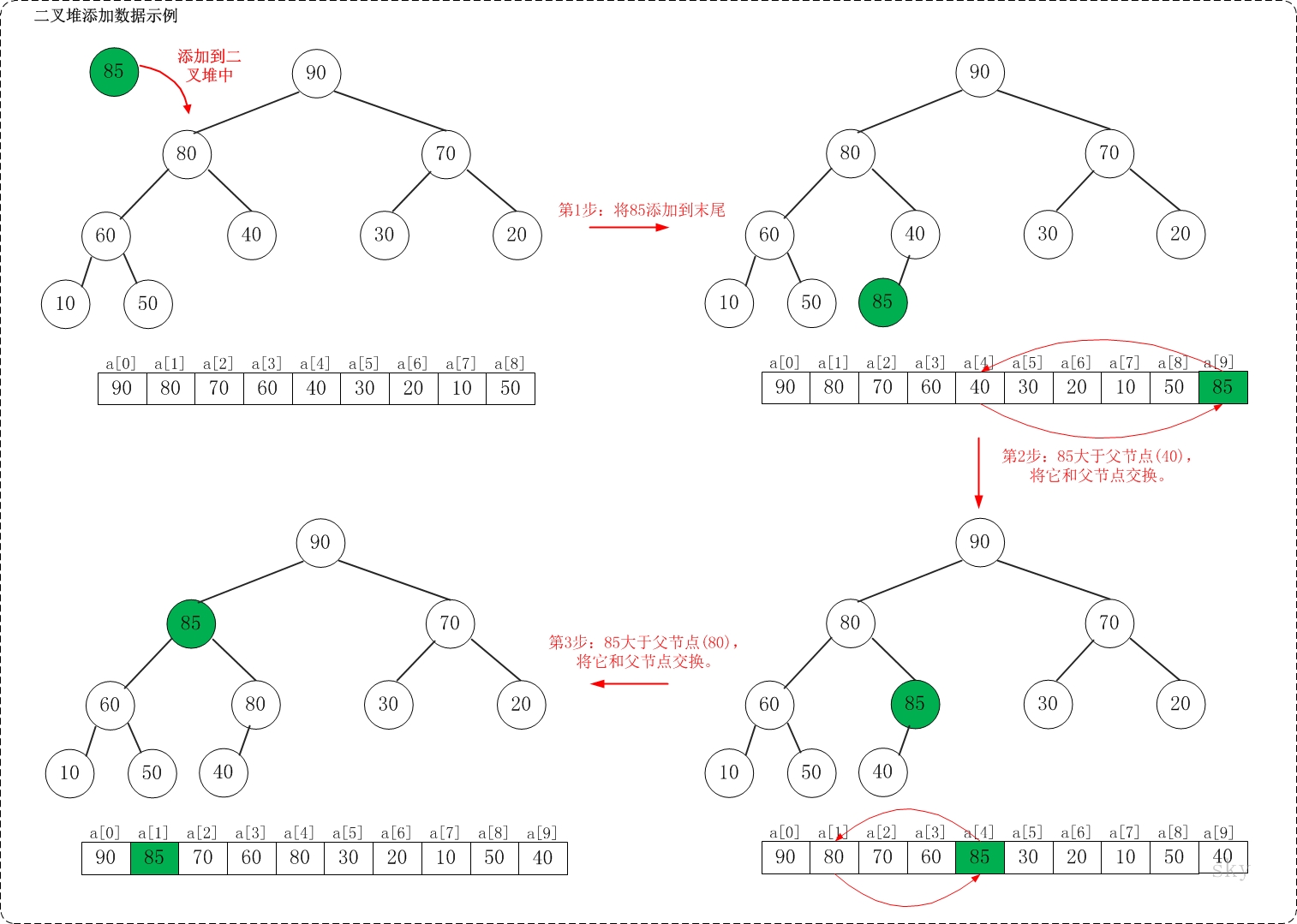
堆添加

先把元素添加到末尾，再依次向上面调整，若大于父节点，就和父节点交换。

堆删除

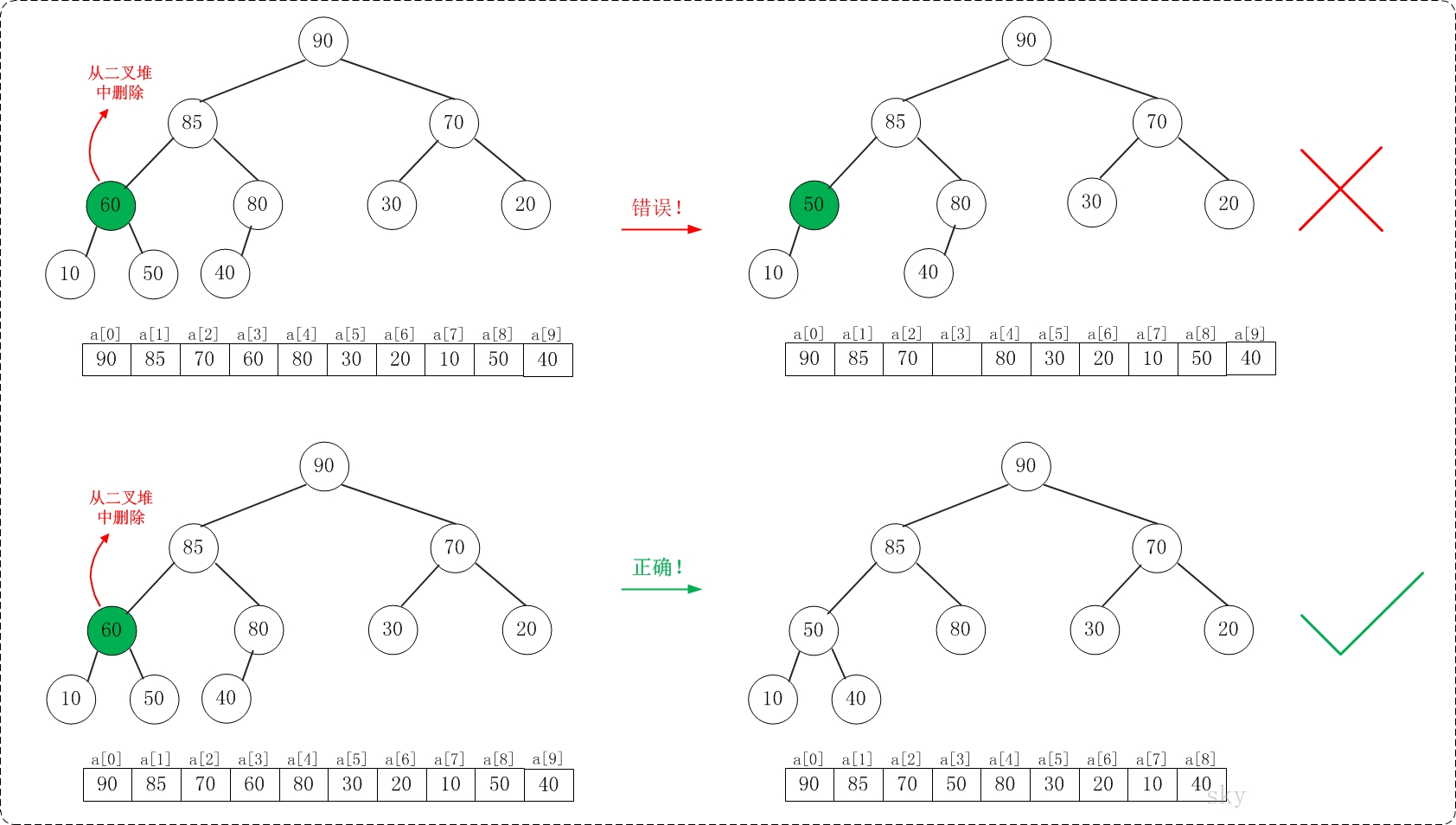
删除堆顶元素：把末尾元素，放到堆顶，再依次向下调整，每次选择较大的子节点进行交换。

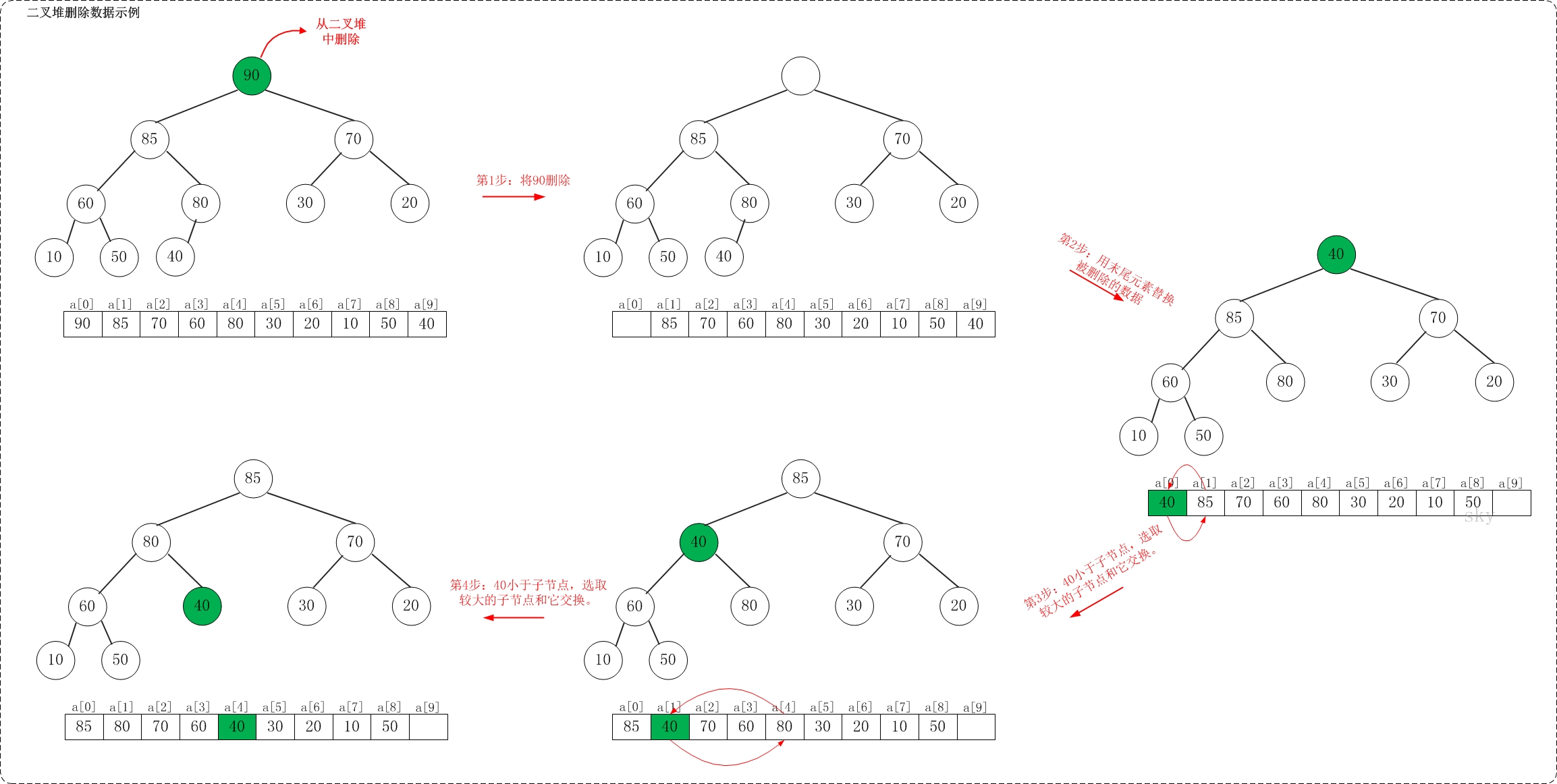
删除堆中元素：把末尾元素，放入空白处，再调整堆即可。

堆排序

思路

1. 初始化堆。把$a_1,\cdots ,a_n$构造成为最大堆
2. 取出最大值。每次出堆根最大元素。出$a_1$，把$a_n$放到$a_1$上，再把$a_1,\cdots .a_{n-1}$调整为最大堆。再出元素
3. 重复2

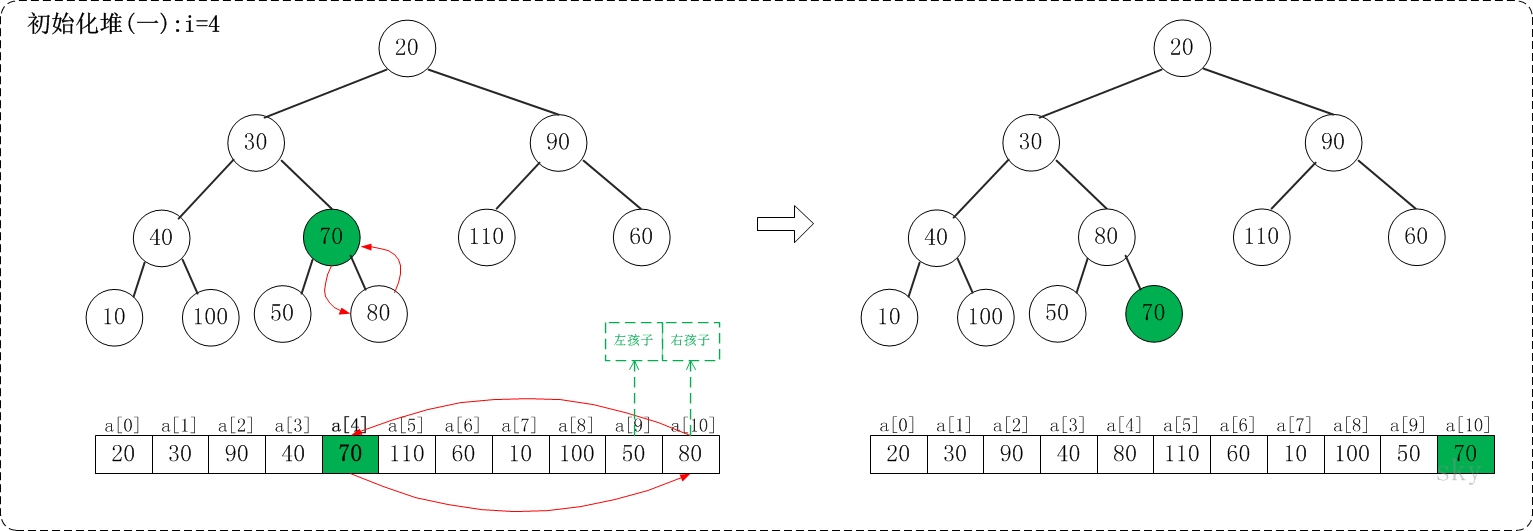
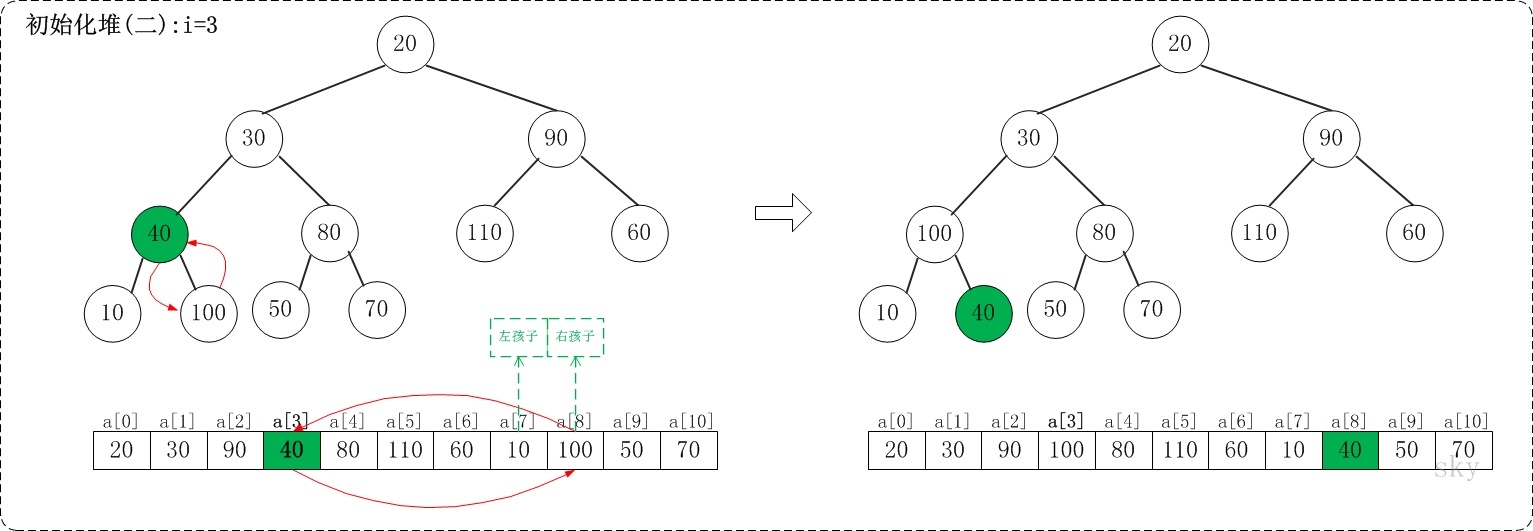
建立堆

n个元素，最后一个父亲节点$\lfloor n/2\rfloor$， 下标为$k=\lfloor n/2\rfloor -1$。

对这些节点$a_k,\cdots ,a_0$， 依次调整它们的子树，使子树成堆。即，若根节点小于左右节点的较大值，则交换。

建立堆实例

对于数据20,30,90,40,70,110,60,10,100,50,80，建立为最大堆110,100,90,40,80,20,60,10,30,50,70

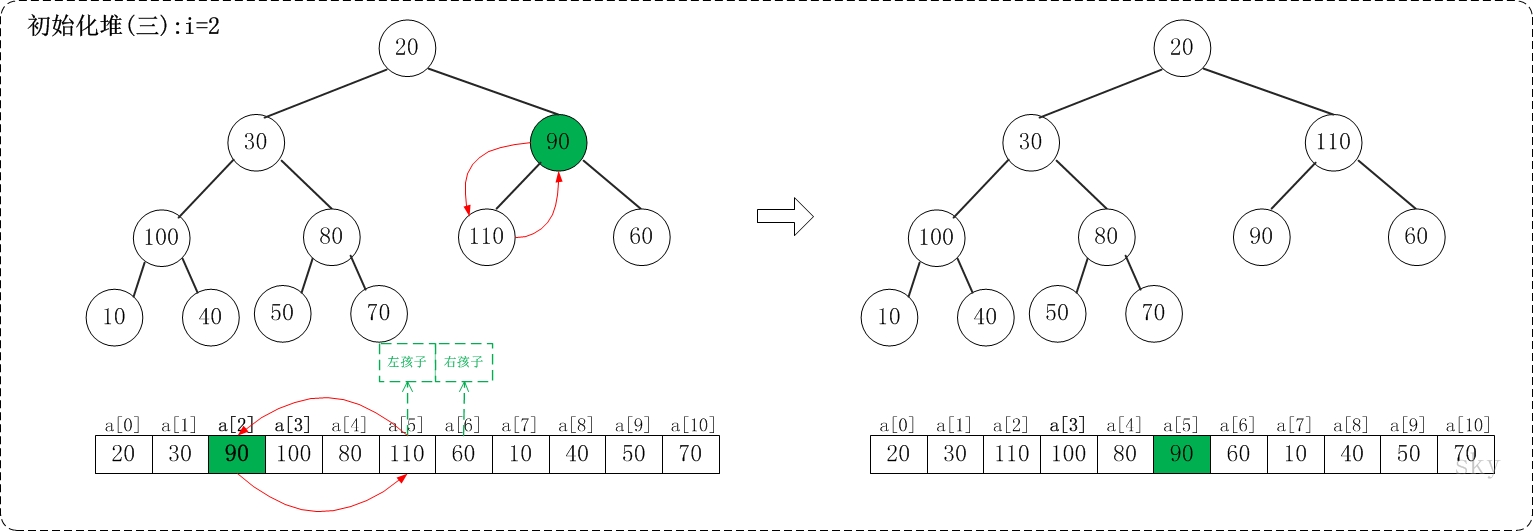
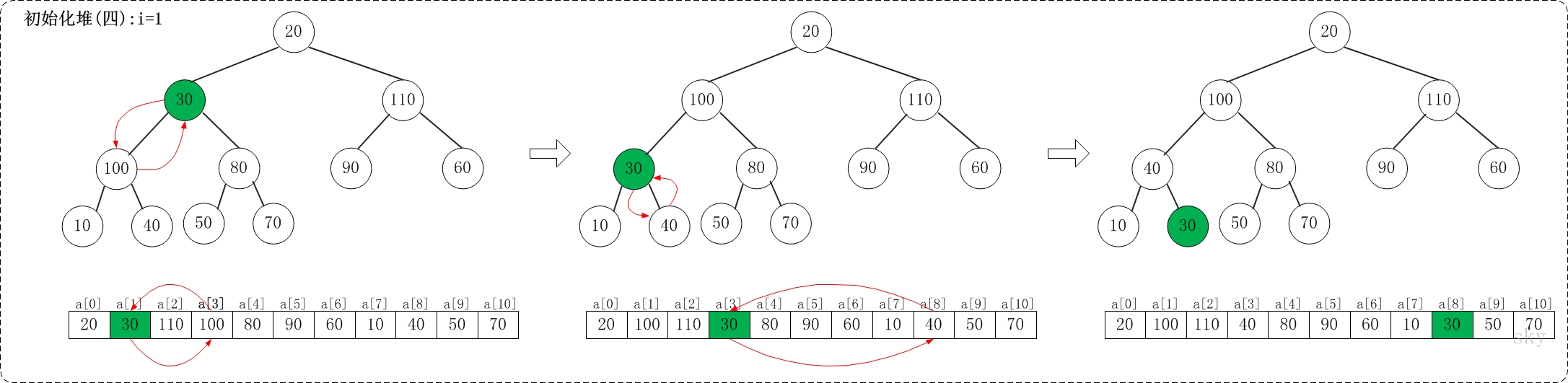
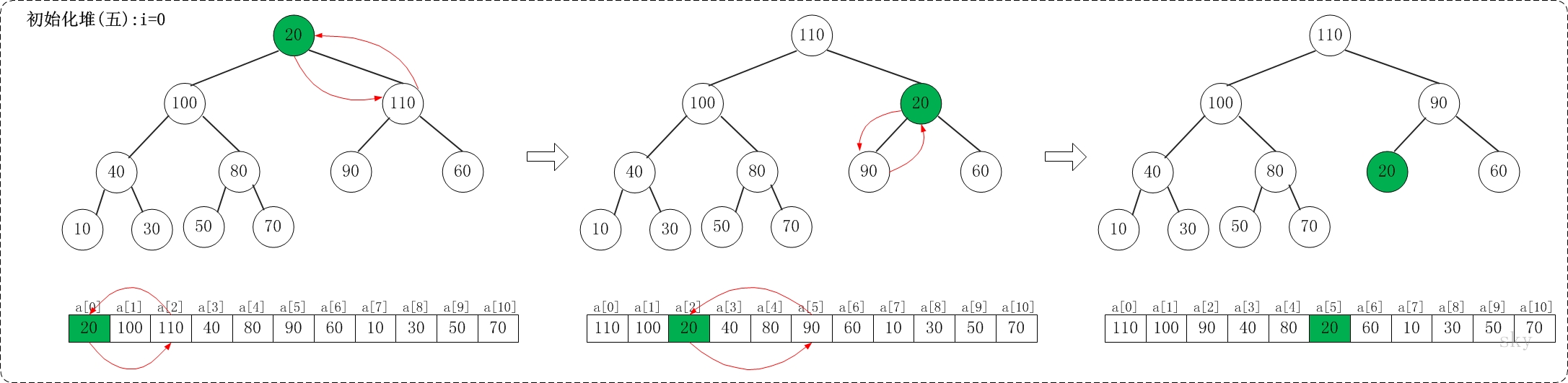
取出最大值

把根节点（最大值）和当前堆的末尾值进行交换，最大值放到最后。再对剩余的数据进行成堆，再依次取最大值交换。

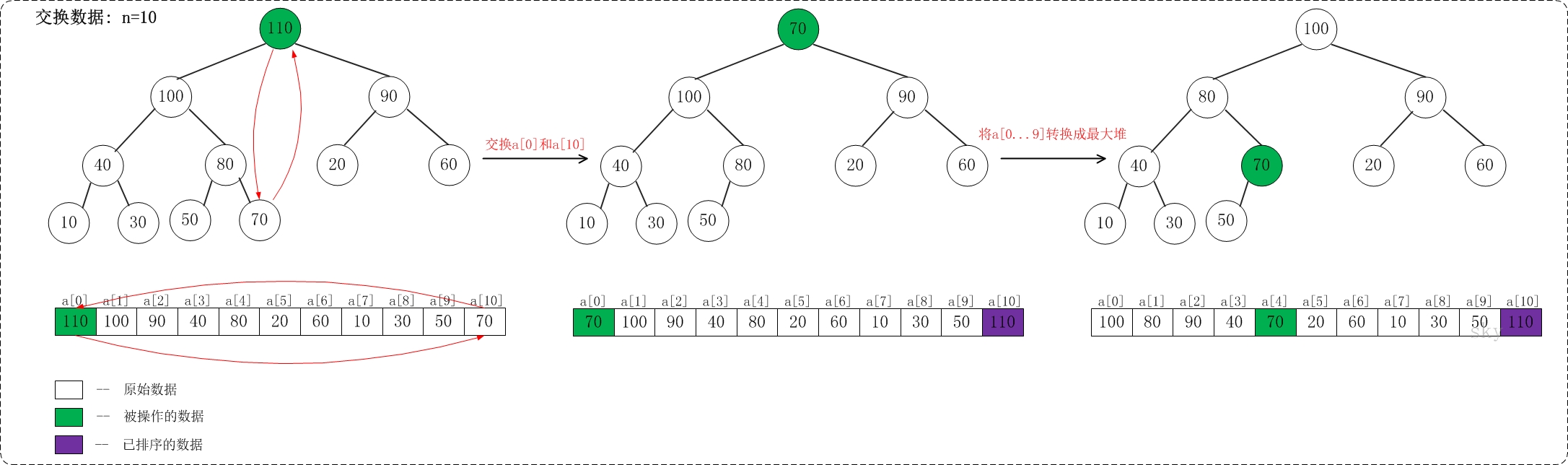
每一次取出最大值重新恢复堆，要$O(\log n)$，有n个数，一共是$O(n\log n)$。

关键代码

/**
 * 保证以start为根节点的子树是一个最大堆，末尾元素为end
 * 
 * Args:
 *      a: 存放堆的数组
 *      start: 根节点
 *      end: 子树的末尾元素
 * Returns:
 *      None
 **/ 
void max_heap_down(vector<int>& a, int start, int end) {
    // 当前节点
    int c = start;
    // 左孩子
    int l = 2 * c + 1;
    // 当前父亲节点
    int t = a[c];
    for (; l <= end; c = l, l = 2*c + 1) {
        // 选择较大的孩子与父亲交换
        if (l + 1 <= end && a[l] < a[l + 1]) {
            // 有右孩子，并且右孩子比左孩子大，则选择右孩子
            l++;
        }
        if (t >= a[l]) {
            // 父亲大于孩子
            break;
        } else {
            // 交换
            a[c] = a[l];
            a[l] = t;
        }
    }
}


/**
 * 堆排序，升序
 **/
void heap_sort_asc(vector<int>& a) {
    int n = a.size();
    // 初始化一个最大堆
    for (int i = n / 2 - 1; i >= 0; i--) {
        max_heap_down(a, i, n - 1);
    }
    // 依次取堆顶元素放到末尾
    for (int i = n - 1; i >= 0; i--) {
        // max放到a[i]
        int t = a[i];
        a[i] = a[0];
        a[0] = t;
        // 保证a[0...i-1]依然是个最大堆
        max_heap_down(a, 0, i-1);
    }
    return;
}

总结分析

名称	时间	最好	最差	空间	稳定	备注
堆排序	$O(n\log n)$	$O(n\log n)$	$O(\log n)$	$O(n)$	不稳定

归并排序

从上往下-递归

思路

• 分解 -- 将区间一分为二，求分裂点$\mathrm{m}\mathrm{i}\mathrm{d}=\frac{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}+\mathrm{e}\mathrm{n}\mathrm{d}}{2}$
• 递归求解，sort， sort -- 递归对两个无序子区间 $a_s,\cdots ,a_m$和$a_{m+1},\cdots ,a_e$进行归并排序。终结条件是子区间长度为1
• 合并，merge -- 把两个有序的子区间 $a_s,\cdots ,a_m$和$a_{m+1},\cdots ,a_e$ 合并为一个完整的有序区间$a_s,\cdots ,a_e$

分解

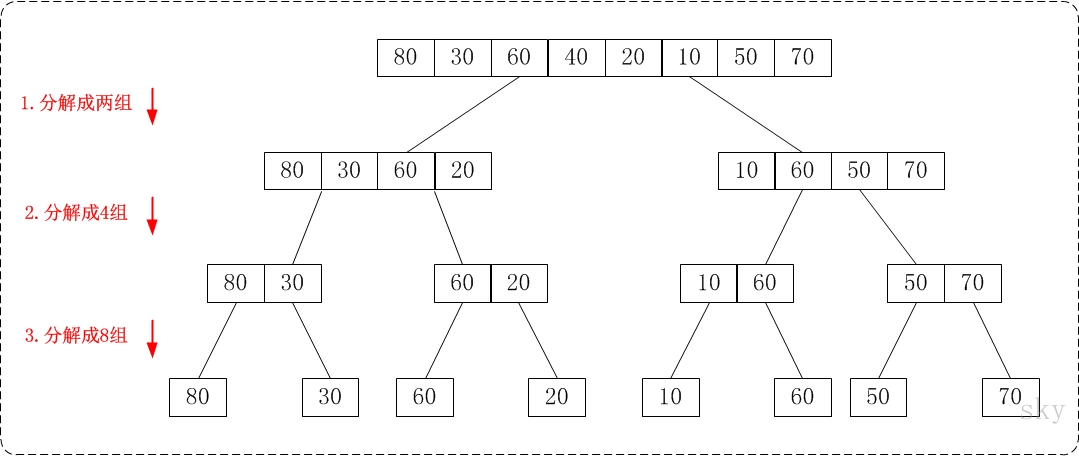
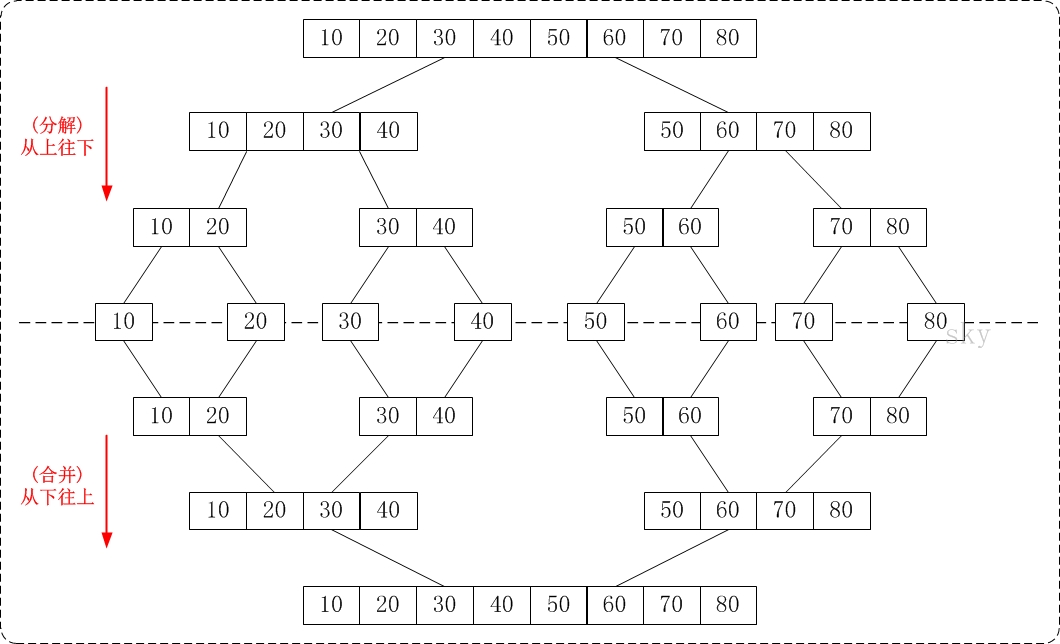
分解&递归&合并

关键代码

/**
 * 归并排序，从上到下
 **/
void merge_sort_up2down(vector<int> &a, int start, int end) {
    if (start >= end) {
        return;
    }
    int mid = (start + end) / 2;
    // 递归排序a[start...mid]
    merge_sort_up2down(a, start, mid);
    // 递归排序a[mid+1...end]
    merge_sort_up2down(a, mid + 1, end);
    // 两个有序序列merge在一起
    merge(a, start, mid, end);
}


/**
 * 将a中前后两个有序序列合并在一起
 **/ 
void merge(vector<int> &a, int start, int mid, int end) {
    // 把有序序列临时存放到t中
    int * t = new int [end - start + 1];
    int i = start;
    int j = mid + 1;
    int k = 0;
    // 依次合并
    while (i <= mid && j <= end) {
        if (a[i] < a[j]) {
            t[k++] = a[i++];
        } else {
            t[k++] = a[j++];
        }
    }

    while (i <= mid) {
        t[k++] = a[i++];
    }

    while (j <= end) {
        t[k++] = a[j++];
    }
     
    // 把新的有序列表复制回a中
    for (int i = 0; i < k; i++) {
        a[start + i] = t[i];
    }

    delete [] t;
}

从下往上-非递归

思想

把数组分成若干个长度为1的子数组，再两两合并；得到长度为2的数组，再两两合并；依次反复，直到形成一个数组。

关键代码

/**
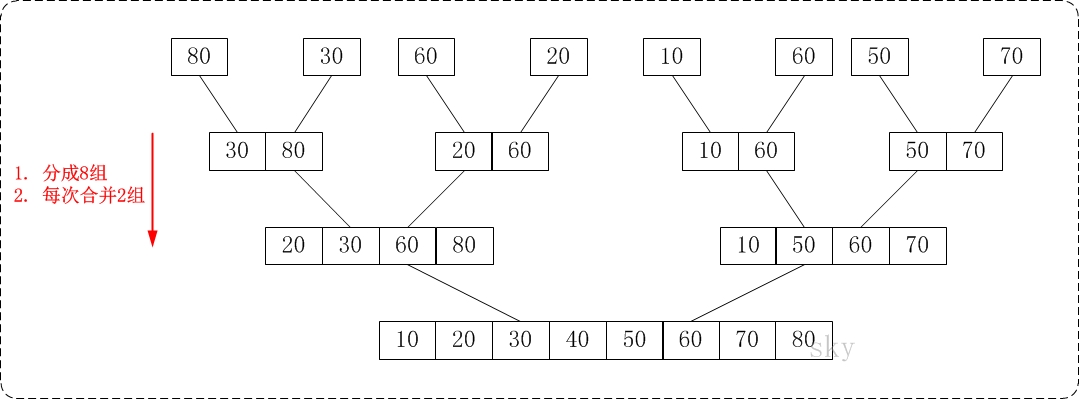
 * 归并排序，从下到上
 **/
void merge_sort_down2up(vector<int> &a) {
    if (a.size() <= 0) 
        return;
    for (int i = 1; i < a.size(); i = i * 2)
        merge_groups(a, i);
}

/*
 * 对a做若干次合并，分为若干个gap。对每相邻的两个gap进行合并排序
 * Args:
 *      a: 数组
 *      gap: 一个子数组的长度
 */
void merge_groups(vector<int> &a, int gap) {
    int twolen = 2 * gap;
    int i;
    for (i = 0; i + twolen - 1 < a.size(); i += twolen) {
        int start = i;
        int mid = i + gap - 1;
        int end = i + twolen - 1;
        merge(a, start, mid, end);
    }
    // 最后还有一个gap
    if (i + gap - 1 < a.size() - 1) {
        merge(a, i, i + gap - 1, a.size() - 1);
    }
}

总结分析

名称	时间	最好	最差	空间	稳定	备注
归并排序	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$， merge占用	稳定

归并排序的形式是一颗二叉树，遍历的次数就是二叉树的深度$O(\log n)$， 而一共n个数。

桶排序

桶排序很简单。数组a有n个数，最大值为max。则，建立一个长度为max的数组b，初始化为0。

遍历a，遇到$a_i=k$， 则$b_k+=1$ 。即在对应的桶里计数加1。

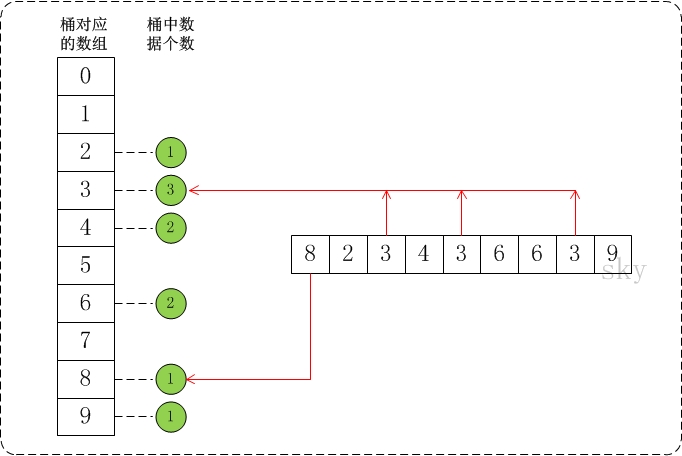
基数排序

基数排序分为最高位优先和最低位优先。

基数排序是桶排序的扩展。把所有的数，统一位数。然后，按照每一位进行，从低位到高位跑排序。

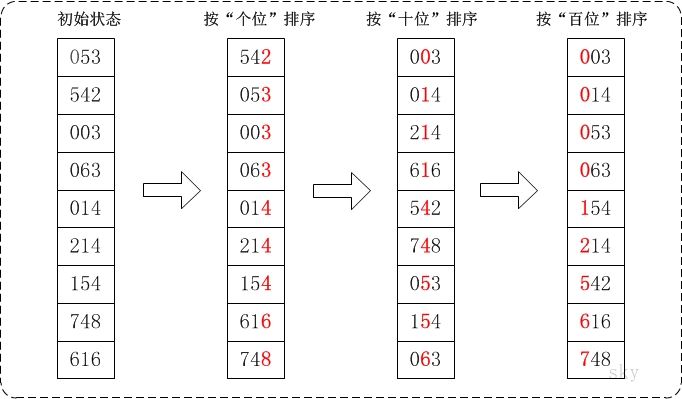
关键是找到output和buckets的对应关系。每个bucket存储前面累积的元素的数量。

buckets[2] = 1;
// 说明排序数是2的元素有1个
buckets[3] = 4;
// 说明排序数是3的元素有 4-1=3个
buckets[4] = 7;
// 说明排序数是4的元素有 7-4=3个

后面在进行根据排序数找到当前数的最终所在位置的时候，就会利用这个关系。

// 比如排序数是3的数字，会出现3个
// 则id就为 buckets[3]-1
// 每出现一个，则buckets[3]--

// 举个例子
// 初始buckets[2]=1，则这1个数字的最终序号是：0
// 初始buckets[3]=4，则这3个数字的最终序号是：3,2,1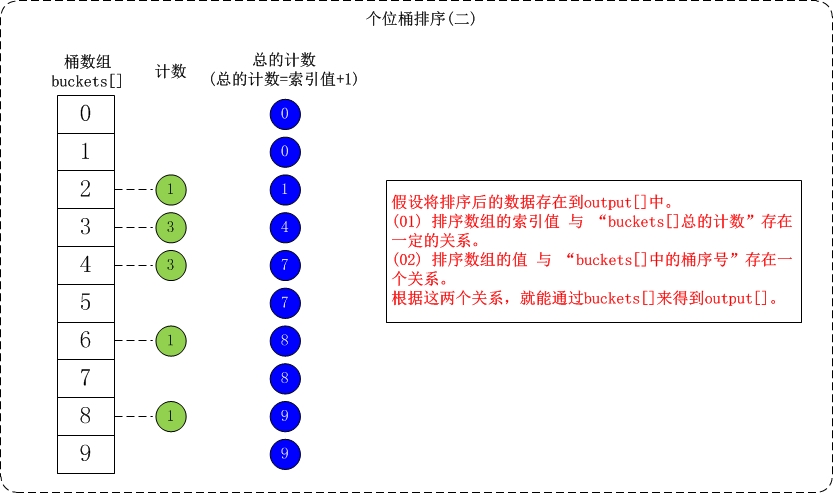

关键代码

/*
 * 基数排序
 */
void radix_sort(vector<int> &a) {
    if (a.size() <= 1) {
        return;
    }

    int max = *max_element(a.begin(), a.end());
    // exp=1, 10, 100, 1000...
    for (int exp = 1; max / exp > 0; exp *= 10) {
        count_sort(a, exp);
    }
}


/*
 * 对数组按照某个位数进行排序
 * Args:
 *      a -- 数组
 *      exp -- 指数，1, 10, 100... 分别按照个位、十位、百位排序
 * Returns:
 *      None
 */
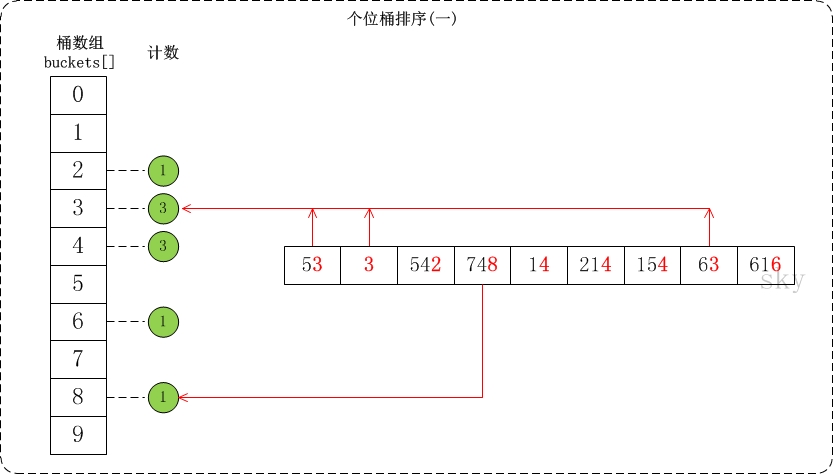
void count_sort(vector<int>& a, int exp) {
    // 存储被排序数据的临时数组
    int output [a.size()];

    // 桶 数据的出现次数
    int buckets[10] = {0};
    for (int i = 0; i < a.size(); i++) {
        int t = (a[i] / exp) % 10;
        buckets[t]++;
    }

    // 根据前面的出现次数，推算出当前数字在原数组中的index
    for (int i = 1; i < 10; i++) 
        buckets[i] += buckets[i - 1];

    // 将数据存储到output中
    for (int i = a.size() - 1; i >= 0; i--) {
        int j = (a[i] / exp) % 10;
        int k = buckets[j];
        output[k - 1] = a[i];
        buckets[j]--;
    }

    // 赋值给a
    for (int i = 0; i < a.size(); i++) {
        a[i] = output[i];
    }
}

总结分析

名称	时间	最好	最差	空间	稳定	备注
基数排序	$O(d(n+r))$	$O(d(n+r))$	$O(d(n+r))$	$O(r)$， r个队列	稳定

总结比较

总结

思想总结

名称	一句话描述
直接插入	前面有序，为新来的，在前面找到合适的位置，进行插入
折半插入	前面有序，为新来的，使用折半查找到插入位置，进行插入
希尔排序	gap个间隔为gap的子序列，每个进行直接插入排序；减小gap，依次排序，直至为1
冒泡排序	交换n-1趟，$a_{i-1}>a_i$，则进行交换，每一趟都有个最大的沉到末尾
快排	第一个数x，先划分，左边小于x，中间x，右边大于x。再依次递归排序左右两边
简单选择	前面有序，从后面选择最小的与前面末尾的（最大的）进行交换
堆排序	初始化大根堆，堆顶和末尾元素交换，再调整使剩下的元素成堆， 重复
归并排序	分解为左右两个序列，对左右两个序列进行递归归并排序，再合并。即sort,sort,merge
基数排序	位数一样，从低位到高位，分别按照每一位进行排序

时空复杂度总结

名称	时间	最好	最差	空间	稳定
直插	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	是
希尔				$O(1)$	不稳定
冒泡	$O(n^2)$	$O(n)$	$O(n^2)$	$O(1)$	是
快排	$O(n\log n)$	$O(n\log n)$	$O(n^2)$	$O({\log }_{2}n)$，栈的深度	不稳定
简选	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	不稳定
堆排序	$O(n\log n)$	$O(n\log n)$	$O(\log n)$	$O(n)$	不稳定
归并排序	$O(n\log n)$	$O(n\log n)$	$O(n\log n)$	$O(n)$， merge占用	稳定
基数排序	$O(d(n+r))$	$O(d(n+r))$	$O(d(n+r))$	$O(r)$， r个队列	稳定

稳定的：插、冒、归、基

较快的：快、些、归、堆，插得好、冒得好

比较次数与初始状态无关：选择、归并

排序趟数与初始状态无关：选择、插入、基数

冒、选、堆：每趟都有1个在最终的位置，最大or最小

直接插入：第$i$趟，前$i+1$个有序，但不是最终序列

快排： $i$趟后， 至少有$i$个在最终位置

时间复杂度：快些归堆$O(n\log n)$，基数排序$O(d(n+r))$ ， 其余$O(n^2)$ ，

空间复杂度：归$O(n)$， 快$O(\log n)$， 基$O(r)$， 其余$O(1)$

算法选择

条件	可选算法
n较小， $n\le 50$	直接插入、简单选择
基本有序	直接插入、冒泡
n较大，要$O(n\log n)$	快排、堆排（不稳定），归并排序（稳定）
n较大，要快，要稳定	归并排序，与直插结合的改进的归并排序
n很大，位数很少，可以分解	基数排序
记录本身信息量太大	为了避免移动，可以使用链表作为存储结构