决策树的特征选择、生成、剪枝。熵、信息增益、基尼指数。ID3、C4.5、CART。
决策树背景
概览
树的意义
决策树是一棵if-then树。 内部节点代表一个属性或特征,叶节点代表一个类。
决策树也是给定各个特征的情况下,某类别的概率。即条件概率\(P(Y \mid X)\)。
树的生成
构建根节点,选择最优特征。按照特征划分子集,继续选择新的最优特征,直到没有或者全部被正确分类。
剪枝
决策树的生成对应于模型的局部选择,会尽量拟合训练数据,导致模型复杂和过拟合。
决策树的剪枝对应于模型的全局选择, 自下而上删掉一些节点。
熵和信息增益
在每个节点,要选择一个最优特征生成。
ID3使用信息增益最大选择最优特征C4.5使用信息增益率最大来选择最优特征CART回归树,平方误差最小CART分类树,基尼指数最小
信息量
信息量是随机变量\(X\)不确定性的度量。 \[
I(X) = - \log p(x)
\] 熵
熵是信息量的期望,也是随机变量不确定性的度量。熵偏向离散属性, 基尼指数偏向连续属性。
\[
H(X) = - \sum_{x \in X} p(x) \log p(x)
\] 条件熵
条件熵是在给定随机变量\(X\)的情况下,随机变量\(Y\)的不确定性。
\[
H(Y \mid X) = \sum_{i = 1}^K p(x_i) H(Y \mid X = x_i)
\] \(X\)共有K类,\(p(x_i)\)表示\(X\)属于第\(i\)类的概率。\(H(Y\mid X=x_i)\)表示\(X=x_i\)时\(Y\)的子集的熵。
经验熵和经验条件熵
由数据估计(极大似然估计)得到的熵和条件熵。
如数据集D,有K个类别。经验熵是 \[
H(D) = -\sum_{k=1}^K \frac{\vert C_k\vert}{\vert D\vert} \log_2 \frac{\vert C_k\vert}{\vert D\vert}
\] 特征A根据取值把数据集D划分为n个子集,则给定特征A时数据集D的经验条件熵是: \[
H(D \mid A) = \sum_{i=1}^n \frac{\vert D_i\vert}{\vert D\vert} H(D_i)
= -\sum_{i=1}^n \frac{\vert D_i\vert}{\vert D\vert} \sum_{k=1}^K \frac{\vert D_{ik}\vert}{\vert D_i\vert} \log_2 \frac{\vert D_{ik}\vert}{\vert D_i\vert}
\] 信息增益
信息增益是给定特征A,使得数据集D不确定性减少的程度。信息增益 = 划分前熵 - 划分后熵 = 熵 - 条件熵 \[
g(D, A) = H(D) - H(D \mid A)
\] 特征A的信息增益越大,不确定性减少越多,A的分类能力就越强。
信息增益的问题
对于取值很多的特征,比如连续型数据(时间)。每一个取值几乎都可以确定一个样本。即这个特征就可以划分所有的样本数据。
信息增益不适合
连续型、取值多的特征- 使得所有分支下的样本集合都是
纯的,极端情况每一个叶子节点都是一个样本 数据更纯,信息增益更大,选择它作为根节点,结果就是庞大且深度很浅的树
信息增益比
数据集\(D\)关于特征A的熵,\(n\)是特征A的取值个数: \[
H_A(D) = -\sum_{i=1}^n
\frac{\vert D_i\vert}{\vert D\vert} \log_2 \frac{\vert D_i\vert}{\vert D\vert}
\] 信息增益比 = 信息增益 / 划分前熵 = 信息增益 / D关于特征A的熵 : \[
g_R(D, A) = \frac {g(D, A)}{H_A(D)} = \frac {H(D) - H(D \mid A)}{H_A(D)}
\] 解决信息增益的问题:特征A分的类别越多,\(D\)关于A的熵就越大,作为分母,所以信息增益\(g_R(D, A)\) 就越小。在信息增益的基础上增加了一个分母惩罚项。
信息增益比的问题:实际上偏好可取类别数目较少的特征。
基尼指数
CART分类树使用基尼指数来选择最优特征。 基尼指数也是度量不确定性。 熵偏向离散属性, 基尼指数偏向连续属性。
概率分布基尼指数
分类中,有\(K\)类。 样本属于第\(k\)类的概率为\(p_k\)。 \[ \rm{Gini}(p) = \sum_{k=1}^K p_k(1-p_k) = 1 - \sum_{k=1}^Kp_k^2 \] 样本集合基尼指数
集合D,有\(K\)类,\(D_k\) 是第k类的样本子集。则D的基尼指数 \[ \rm{Gini}(D) = 1 - \sum_{k=1}^K \left(\frac{\vert D_k\vert}{\vert D\vert} \right)^2 \] 特征A条件基尼指数
特征A取值为某一可能取值为a。 根据A是否取值为a把D划分为\(D_1\)和\(D_2\)两个集合。
在特征A的条件下,D的基尼指数如下: \[ \rm{Gini}(D, A) = \frac{\vert D_1\vert}{\vert D\vert} \rm{Gini}(D_1) + \frac{\vert D_2\vert}{\vert D\vert} \rm{Gini}(D_2) \] \(\rm{Gini}(D, A)\)是集合D根据特征A分割后,集合D的不确定性。
ID3算法
决策树的生成,ID3算法以信息增益最大为标准选择特征。递归构建,不断选择最优特征对训练集进行划分。
递归终止条件:
- 当前节点的所有样本,属于同一类别\(C_k\),无需划分。该节点为叶子节点,类标记为\(C_k\)
- 当前属性集为空,或所有样本在属性集上取值相同
- 当前节点的样本集合为空,没有样本
在集合D中,选择信息增益最大的特征\(A_g\) :
增益小于阈值,则不继续向下分裂,到达叶子节点。该节点的标记为该节点所有样本中的majority class\(C_k\)。 这也是预剪枝增益大于阈值,按照特征\(A_g\)的每一个取值\(A_g=a_i\)把D划分为各个子集\(D_i\),去掉特征\(A_g\)
继续对每个内部节点进行递归划分。
C4.5算法
C4.5是ID3的改进,C4.5以信息增益率最大为标准选择特征。
ID3/C4.5决策树剪枝
决策树的生成,会过多地考虑如何提高对训练数据的分类,从而构建出非常复杂的决策树。就容易过拟合。
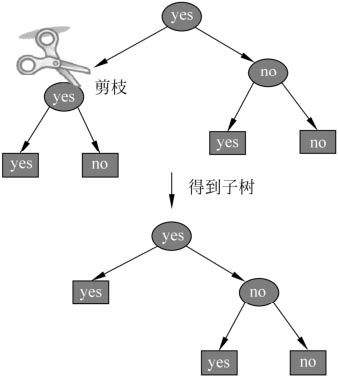
剪枝就是裁掉一些子树和叶节点,并将其根节点或父节点作为叶节点。剪枝分为预剪枝和后剪枝。
预剪枝
在生成树的时候,设定信息增益的阈值,如果某节点的某特征的信息增益小于该阈值,则不继续分裂,直接设为叶节点。选择该节点的D中类别数量最多的类别 (majority class)作为类别标记。
后剪枝
树构建好以后,基于整体,极小化损失函数,自下而上地进行剪枝。
树T的参数表示
- 叶节点的个数\(\vert T \vert\)
- 叶节点\(t\)
- 叶节点\(t\)上有\(N_t\)个样本
- 有\(K\)类
- 叶节点t上的经验熵\(H_t(T)\)
- \(\alpha \ge 0\) 为惩罚系数
叶节点t上的经验熵 \[
H_t(T) = -\sum_{k=1}^K \frac{N_{tk}}{N_t} \log \frac{N_{tk}}{N_t}
\] 模型对训练数据的拟合程度\(C(T)\) ,所有叶节点的经验熵和: \[
C(T) = \sum_{t=1}^{\vert T \vert} N_tH_t(T)
\] 最终损失函数 = 拟合程度 + 惩罚因子: \[
C_\alpha(T) = C(T) + \alpha \vert T\vert
\] 参数\(\alpha\)权衡了训练数据的拟合程度和模型复杂度。
- \(\alpha\)大,决策树简单,拟合不好
- \(\alpha\)小,决策树复杂,过拟合
剪枝步骤
- 计算每个节点的经验熵
- 递归从树的叶节点向上回缩。叶节点回缩到父节点:整体树:回缩前\(T_1\) ,回缩后\(T_2\)
- \(C_\alpha(T_2) \le C_\alpha(T_1)\), 则
回缩到父节点,父节点变成新的叶节点。
CART-回归树
Classification and regression tree分类与回归树。
- 回归-平方误差最小
- 分类-基尼指数最小
二叉树- 内部节点:是 - 否。如特征$A a $或 \(A > a\)
模型
把输入空间划分为M个单元\(R_1,R_2,\cdots, R_M\), 每个单元有多个样本,有一个固定的输出值\(c_m\)。 \[
\hat c_m = \rm{avg} (y_i), \; y_i \in R_m
\] 树模型 : \[
f(x) = \sum_{m=1}^M c_m I(x \in R_m)
\] 划分单元
寻找最优切分变量j和最优切分点s 。
选择第\(j\)个变量\(x^{(j)}\)和其取值\(s\), 作为切分变量和切分点,划分为两个空间 \(R_1, R_2\),输出分别为\(c_1, c_2\) : \[
R_1(j, s) = \{x \mid x^{(j)} \le s \}, \quad \quad R_2(j, s) = \{x \mid x^{(j)} > s \}
\] 求最优,平方误差最小 : \[
\min_\limits{j, s} \left[
\min_\limits{c_1} \sum_{x_i \in R_1(j, s)} (y_i - c_1)^2 +
\min_\limits{c_2} \sum_{x_i \in R_1(j, s)} (y_i - c_1)^2
\right]
\] 对每个区域重复划分过程,直到停止。也叫作最小二乘回归树。
CART-分类树
基尼指数最小原则 。
对每一个数据集D,对每一个特征A,对每一个A的取值\(A=a\) 是或者否,划分两个自己\(D_1\)和\(D_2\)
- 计算在特征\(A=a\)条件下的基尼指数\(\color{blue} {\rm{Gini}(D, A=a)}\)
- 选择
基尼指数最小特征A及其取值a,作为最优特征和最优切分点 - 从现节点
划分为两个子节点
CART剪枝
剪枝总体步骤
从生成的决策树\(T_0\)开始, 从底端向上开始剪枝,直到\(T_0\)的根节点。
损失函数决定是否剪枝- 形成子树序列\(\{T_0, T_1, \cdots, T_n\}\)
交叉验证子树序列,选择最优子树
K-折交叉验证法
数据集划分为K个子集。每个子集分别做一次验证集,其余K-1组作为训练集。得到K个模型。
剪枝损失函数 \[
C_\alpha(T) = C(T) + \alpha \vert T\vert
\] \(C(T)\)为所有叶节点的经验熵和 : \[
C(T) = \sum_{t=1}^{\vert T \vert} N_tH_t(T)
\] \(\alpha\)权衡训练数据拟合程度和模型复杂度。
整体树\(T_0\)的任意内部节点t, \(\alpha\)从0开始,每次一个小区间\([\alpha_i, \alpha_{i+1})\) :
t为单节点树时损失:\(C\alpha(t) = C(t) + \alpha\)t为根节点子树时损失:\(C_\alpha(T_t) = C(T_t) + \alpha \vert T_t\vert\)- \(\alpha=0\)时, \(C\alpha(t) < C_\alpha(T_t)\) 。因为,树大,精确,损失小。
- 随着\(\alpha\)的增大,会达到: \(C\alpha(t) = C_\alpha(T_t)\)
求得临界点\(\alpha\) \[
\alpha = \frac{C(T) - C(T_t)} {\vert T_t\vert - 1}
\] 对每个内部节点求: \[
g(t) = \frac{C(T) - C(T_t)} {\vert T_t\vert - 1}
\]
- 在\(T_0\)中减去
最小的\(g(t)\)对应的子树\(T_t\) , 作为\(T_1\) - t节点作为叶子节点,类标记为
majority class - 最后再交叉验证所有的子树序列即可
