SVM笔记

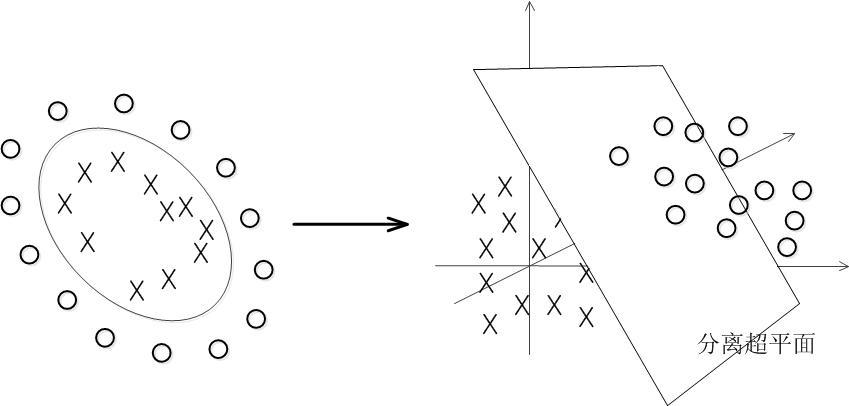
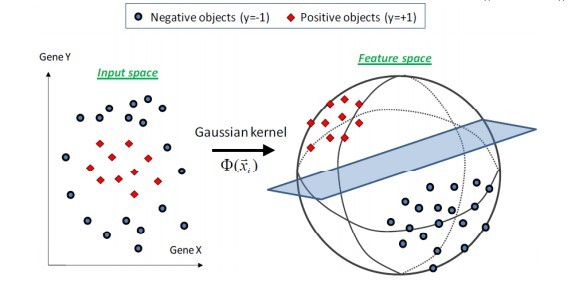
Support Vector Machine简单笔记。 特征空间上的间隔最大的线性分类器。学习策略是间隔最大化，转化为一个凸二次规划问题的求解。

SVM概览

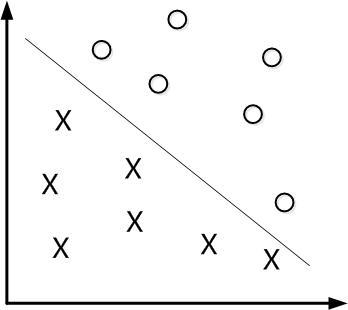
线性分类器

逻辑回归的图像和公式如下，预测的分类为1的概率。

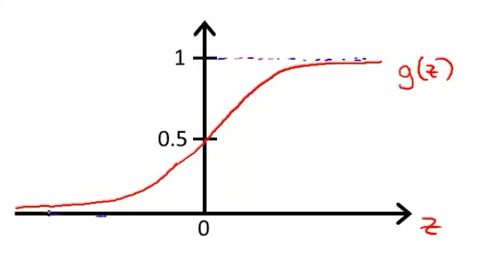\[ h_\theta(x) = g(\theta^Tx), \quad g(z) = \frac{1}{1+e^{-z}}, \quad g(z) = \begin{cases} 1, & z\ge 0 \\ -1, & z < 0 \\ \end{cases} \]

\[ y = \begin{cases} 1, \; & h_\theta(x) \ge 0.5, \;即\; \theta^Tx \ge 0\\ 0, \; & h_\theta(x) < 0.5,  \; 即 \; \theta^Tx < 0 \\\end{cases} \]

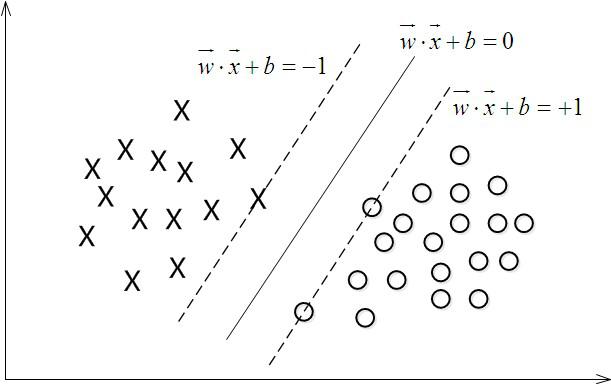
其中\(\theta^Tx=w^Tx+b=0\) 是一个超平面。 用分类函数表示\(f(x)=w^Tx+b\) 。 \(w\)是这个超平面的法向量。

即对于任意一个x，有如下预测类别： \[ \hat y=\begin{cases} 1, & f(x) \ge 0\\ -1, & f(x) < 0 \\ \end{cases} \]

函数间隔与几何间隔

函数间隔

超平面\(w^Tx+b=0\)确定后， \(\vert w\cdot x+b\vert\)表示点x到平面的距离，表示分类可靠性。距离越远，分类越可信。\(y\)与\(w\cdot x+b\)的符号的一致性表示分类的正确性。

超平面\((w,b)\)关于样本点\((x_i, y_i)\)的函数间隔\(\hat \gamma_i\)如下： \[ \hat \gamma_i = y_i (w^T \cdot x_i + b) \] 超平面关于所有样本点的函数间隔\(\hat \gamma​\) ： \[ \hat \gamma = \min \hat \gamma_i \] 函数间隔的问题：w和b成比例改变，超平面未变，但函数间隔已变。

几何间隔

对函数间隔除以法向量的二范数，则得到超平面与点\((x_i,y_i)\)的几何间隔\(\gamma_i\) ： \[ \gamma_i = \frac{\hat \gamma_i}{\|w\|} = \frac{y_i(w^T\cdot x_i + b)}{\|w\|} \] 超平面关于所有样本点的几何间隔： \[ \gamma = \min \gamma_i \] 几何间隔才是直观上点到超平面的距离。

最大间隔分类器

分类时，超平面离数据点的间隔越大，分类的确信度也越大。 所以要最大化这个几何间隔，目标函数如下： \[ L = \max_\limits{w, b} \gamma, \quad s.t,\quad \gamma_i \ge \gamma \]

用函数间隔\(\hat \gamma\)描写为： \[ L = \max_\limits{w, b} \frac{\hat \gamma}{\|w\|}, \quad s.t, \quad \hat \gamma_i \ge \hat \gamma, \; \text{ 其中 }\hat \gamma_i = y_i(w^T \cdot x_i + b) \] 函数间隔\(\hat \gamma​\)的取值并不会影响最优化问题的解。 \(\lambda w, \lambda b \to \lambda \hat \gamma​\)

目标函数

取函数间隔为1，\(\hat \gamma = 1\)， 则有目标函数： \[ L = \max_\limits{w,b} \frac{1}{\|w\|}, \quad s.t, \quad y_i(w^Tx_i+b) \ge 1 \]

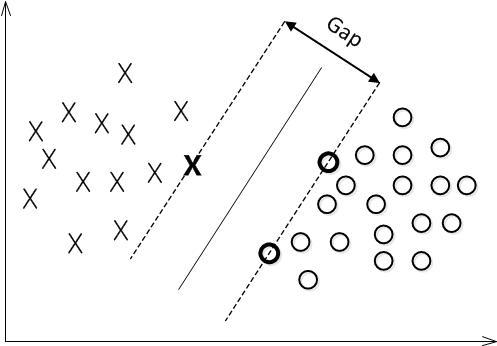
支持向量是虚线边界上的点，则有： \[ \begin{cases} y_i(w^Tx_i+b)=1, & 支持向量 \\ y_i(w^Tx_i+b) >1, & 其他点 \\ \end{cases} \]

分类 \[ \hat y=\begin{cases} 1, & f(x) \ge 0\\ -1, & f(x) < 0 \\ \end{cases} \]

线性SVM

拉格朗日对偶性

1 原始问题

\(f(x), c_i(x), h_j(x)\)都连续可微。

最优化： \[ \min_\limits{x\in R} f(x) \] 有很多个约束条件（不等式约束和等式约束）： \[ c_i(x) \le 0 ,\quad h_j(x) = 0 \] 求解原始问题

将约束问题无约束化。

引入拉格朗日函数，其中\(\alpha_i (\ge 0)\)和\(\beta_j\)是拉格朗日乘子
\[ L(x, \alpha, \beta) = f(x) + \sum\alpha_ic_i(x) + \sum \beta_j h_j(x) \] 定义关于\(x\)的函数\(\theta_p(x)\)： \[ \theta_p(x) = \max_\limits{\alpha,\beta:\alpha_i\ge0} L(x, \alpha, \beta) \]

\[ \theta_p(x) = \begin{cases} f(x), &x满足约束 \\ +\infty, & 其他 \\ \end{cases} \]

\(f(x)\)求最小，则对\(\theta_p(x)\)求最小。

原始问题： 先固定x，优化出参数\(\alpha, \beta\)，再优化x。 \[ \min_\limits{x} \; \theta_p(x) = \min_\limits{x} \max_\limits{\alpha, \beta:\alpha_i\ge0} L(x, \alpha, \beta) \] 所以原始最优化问题 变为 拉格朗日函数的极小极大问题。

定义原始问题的最优解\(p^*\) ： \[ p^* = \min_\limits{x} \theta_p(x) \] 2 对偶问题

定义关于\(\alpha, \beta\)的函数\(\theta_d(\alpha, \beta)\) \[ \theta_d(\alpha, \beta) = \min_x L(x, \alpha, \beta) \] 对偶问题：先固定参数\(\alpha, \beta\) ，优化出x，再优化出参数。 先优化x。 \[ \max_\limits{\alpha, \beta:\alpha_i\ge0} \theta_d(\alpha, \beta) = \max_\limits{\alpha, \beta:\alpha_i\ge0} \min_x L(x, \alpha, \beta) \] 原始问题： 先固定x，优化出参数\(\alpha, \beta\)，再优化x。先优化参数。 \[ \min_\limits{x} \; \theta_p(x) = \min_\limits{x} \max_\limits{\alpha, \beta:\alpha_i\ge0} L(x, \alpha, \beta) \] 定义对偶问题的最优值： \[ d^* = \max_\limits{\alpha, \beta:\alpha_i\ge0} \theta_d(\alpha, \beta) \]

3 原始问题与对偶问题的关系

因为： \[ \theta_d(\alpha, \beta) = \min_x L(x, \alpha, \beta) \le \max_\limits{\alpha,\beta:\alpha_i\ge0} L(x, \alpha, \beta) = \theta_p(x) \] 定理1：如果原始问题与对偶问题均有最优值，则有：\(d^* \le p^*\) \[ d^* = \max_\limits{\alpha, \beta:\alpha_i\ge0} \min_x L(x, \alpha, \beta) \le \min_\limits{x} \max_\limits{\alpha, \beta:\alpha_i\ge0} L(x, \alpha, \beta) = p^* \] 推论1：如果\(d^* = p^*\)， 那么\(x^*, \alpha^*, \beta^*\)分别是原始问题和对偶问题的最优解。

通过对偶问题，来解决原始问题。

4 KKT条件

满足什么条件，才能使\(d^* = p^*\)呢 ？

首先满足下面的大条件：

假设\(f(x)\)和\(c_i(x)\)都是凸函数， \(h_j(x)\)是仿射函数；假设不等式约束\(c_i(x)\)是严格可行的。

定理2：则存在解，\(x^*\)是原始问题的最优解，\(\alpha^*, \beta^*\)是对偶问题的最优解。 并且： \[ d^* = p^* = L(x^*, \alpha^*, \beta^*) \] KKT条件：则\(x^*\)是原始问题、\(\alpha^*, \beta^*\)是对偶问题的最优解的充分必要条件是\(x^*, \alpha^*, \beta^*\)满足下面的KKT条件： \[ \begin{align} & 偏导为0条件\\ & \nabla_x L(x^*, \alpha^*, \beta^*) = 0 \\ & \nabla_\alpha L(x^*, \alpha^*, \beta^*) = 0 \\ & \nabla_\beta L(x^*, \alpha^*, \beta^*) = 0 \\ & 约束条件 \\ & c_i(x^*) \le 0 \\ & h_j(x^*) = 0 \\ & \alpha_i^* \ge 0 \\ & \rm{KKT}对偶互补条件 \\ & \alpha_i^* c_i(x^*) = 0 \\ \end{align} \] 由KKT对偶互补条件可知，若\(\alpha_i^* >0\)， 则\(c_i(x^*)=0\) 。SVM推导会用到。

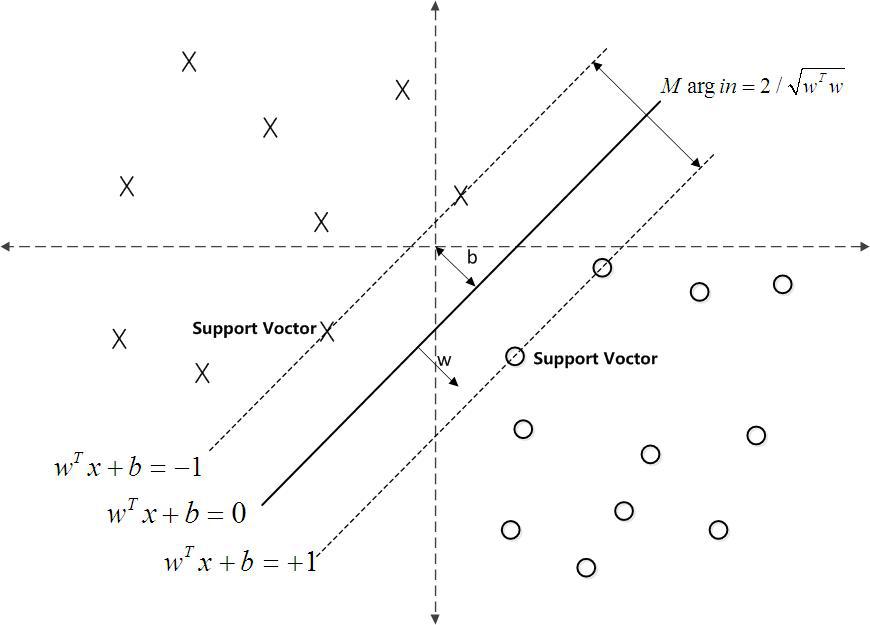
若\(\alpha_i>0\)， 则对应的\(x_i\)是支持向量， 有\(y_i(w^*\cdot x+ b^*) = 1\)。 所有的非支持向量，都有\(\alpha_i =0\)。

原始问题到对偶问题

先前的目标函数： \[ J = \max_\limits{w,b} \frac{1}{\|w\|}, \quad s.t, \quad y_i(w^Tx_i+b) \ge 1 \] 最大变为最小，则有原始问题如下。目标函数是二次的，约束条件是线性的。所以是个凸二次规划问题。 \[ J = \min_{w,b} \frac{1}{2} \|w\|^2, \quad s.t, \quad y_i(w^Tx_i+b) \ge 1 \] 构造拉格朗日函数 ： \[ L(w, b, \lambda) =\frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i \left(y_i(w^Tx_i+b) - 1\right) \] 原始问题 \[ \theta_p(w,b) = \max_{\lambda_i \ge 0} L(w, b, \alpha) \]

\[ p^* = \min_{w, b} \theta_p(w, b) = \min_{w, b} \max_{\lambda_i \ge 0} L(w, b, \alpha) \]

对偶问题 \[ \theta_d(\alpha) = \min_{w,b} L(w, b, \alpha) \]

\[ d^* = \max_{\alpha_i \ge 0} \theta_d(\alpha) = \max_{\alpha_i \ge 0} \min_{w,b} L(w, b, \alpha) \]

我们知道\(d^* \le p^*​\)， 有时相等。原始问题可以转化为对偶问题求解，好处是：近似解，好求解。

求解对偶问题

拉格朗日函数： \[ L(w, b, \lambda) =\frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i \left(y_i(w^Tx_i+b) - 1\right) \] 化简后： \[ L(w, b, \lambda) =\frac{1}{2} \|w\|^2 -\sum_{i=1}^n\alpha_iy_iw^Tx_i- \sum_{i=1}^n\alpha_iy_ib + \sum_{i=1}^n\alpha_i \] 目标函数： \[ d^* = \max_{\alpha_i \ge 0} \theta_d(\alpha) = \max_\limits{\alpha_i \ge 0} \min_\limits{w,b} L(w, b, \alpha) \] 主要是三个步骤：

• 固定参数\(\alpha\)， 求 极小化\(\min_{w,b} L(w, b, \alpha)\)的w和b
  
• 带入w和b，对\(L\)求参数\(\alpha\) 的极大化
• 利用SMO算法求解对偶问题中的拉格朗日乘子\(\alpha\)

1 极小求出w和b \(\min_\limits{w,b} L(w, b, \alpha)\)

对w和b求偏导，使其等于0。 \[ \frac{\partial L}{\partial w} = w -\sum_{i=1}^n\alpha_iy_ix_i \begin{equation}\xlongequal {令}{} 0 \end{equation} \quad \to \quad w = \sum_{i=1}^n\alpha_iy_ix_i \]

\[ \frac{\partial L}{\partial b} = - \sum_{i=1}^n \alpha_iy_i \xlongequal {令}{} 0 \quad \to \quad \sum_{i=1}^n \alpha_iy_i=0 \]

特别地范式求导：\(\frac{\partial \|w\|^2}{\partial w} = 2w​\) \[ \frac{\partial \|w\|^2}{\partial w} = w \] 把上面两个结论，带入原式进行化简，得到： \[ \begin{align} L(w, b, \alpha) &=\frac{1}{2}w^Tw - \sum_{i=1}^n\alpha_iy_iw^Tx_i- \sum_{i=1}^n\alpha_iy_ib + \sum_{i=1}^n\alpha_i \\ & = \frac{1}{2} w^T\sum_{i=1}^n\alpha_iy_ix_i - w^T \sum_{i=1}^n\alpha_iy_ix_i - b\sum_{i=1}^n\alpha_iy_i + \sum_{i=1}^n\alpha_i \quad\text{(带入w，提出b，带入0)}\\ & = -\frac{1}{2}\left(\sum_{i=1}^n\alpha_iy_ix_i\right)^T\left(\sum_{i=1}^n\alpha_iy_ix_i\right) + \sum_{i=1}^n\alpha_i \quad{(只有x是向量，直接转置)}\\ &= -\frac{1}{2}\left(\sum_{i=1}^n\alpha_iy_ix_i^T\right)\left(\sum_{i=1}^n\alpha_iy_ix_i\right) + \sum_{i=1}^n\alpha_i \\ & = \sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j x_i^T x_j \end{align} \] 得到只用\(\alpha\)表示的拉格朗日函数： \[ L(w, b, \alpha) =\sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j x_i^T x_j \] 2 求出对\(\alpha​\)的极大 \(\max_{\alpha_i \ge 0} \theta_d(\alpha) = \max_\limits{\alpha_i \ge 0} \min_\limits{w,b} L(w, b, \alpha)​\)

对偶问题 如下：

目标函数： \[ \max_\limits{\alpha} \; \sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j x_i^T x_j \] 约束条件： \[ \begin{align} &\alpha_i \ge 0 \\ & \sum_{i=1}^n \alpha_iy_i = 0\\ \end{align} \] 利用SMO算法求出拉格朗日乘子\(\alpha^*\)。

3 求出w和b，得到分离超平面和决策函数

根据前面的公式得到\(w^*\)： \[ w* =\sum_{i=1}^n\alpha_i^*y_ix_i \] 选一个\(\alpha^*_j > 0\)对应的点\((x_j, y_j)\) 就是支持向量。由于支持向量\(y_j(w^*\cdot x+ b^*) -1 = 0\) ，\(y_j^2=1\)

得到\(b^*\) ： \[ b^* = y_j - \sum_{i=1}^n\alpha_i^*y_i(x_i\cdot x_j), \quad\quad \text{($x_i\cdot x_j$是向量内积，后面同理)} \] 通过公式可以看出，决定w和b的是支持向量， 其它点对超平面是没有影响的。

分离超平面 \[ f(x) = \sum_{i=1}^n\alpha_i^*y_i(x_i\cdot x) + b^* = 0 \] 分类决策函数 \[ f(x) = \rm{sign}\left(\sum_{i=1}^n\alpha_i^*y_i(x_i\cdot x) + b^* \right) \]

简单总结

目标函数 \[ J = \min_{w,b} \frac{1}{2} \|w\|^2, \quad s.t, \quad y_i(w^Tx_i+b) \ge 1 \] 拉格朗日函数 \[ L(w, b, \lambda) =\frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i \left(y_i(w^Tx_i+b) - 1\right) \] 转化为对偶问题求解， 需要会求解过程、会推导公式。 \[ \max_{\alpha_i \ge 0} \min_{w,b} L(w, b, \alpha) \] 主要是下面4个求解步骤：十分重要!!!

1. 固定\(\alpha\)， L对w和b求偏导，得到两个等式
2. 结果带入L，消去w和b，得到只有\(\alpha\)的L
3. 利用SMO求出\(\alpha^*\)
4. 利用\(\alpha^*\)和支持向量，算出w和b。得出分离超平面和分界函数。

求导后消去w和b，得到L \[ L(w, b, \alpha) =\sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j x_i^T x_j \] 利用SMO求得\(\alpha^*\)后， 带回原式，得到w和b： \[ w* =\sum_{i=1}^n\alpha_i^*y_ix_i, \quad b^* = y_j - \sum_{i=1}^n\alpha_i^*y_i(x_i\cdot x_j), \] 实际上最重要是向量内积来进行决策 \[ f(x) = \rm{sign}\left(\sum_{i=1}^n\alpha_i^*y_i \color{red}{(x_i\cdot x}) + b^* \right) \] 目标函数 \[ \max_\limits{\alpha_i \ge 0}L(w, b, \lambda) = \max_\limits{\alpha_i \ge 0} \frac{1}{2} \|w\|^2 - \sum_{i=1}^n \alpha_i \color{red}{\left(y_i(w^Tx_i+b) - 1\right)} \] 两种数据点

• 支持向量：红色为0，\(\alpha_i > 0\)。 后面为0。
• 其它点：红色大于1，\(\alpha_i=0\)。 后面为0。

非线性SVM

核函数

问题

大部分数据不是线性可分的，前面的超平面根本不存在。可以用一个超曲面进行分离，这就是非线性可分问题。

SVM可以通过核函数把输入映射到高维特征空间，最终在高维特征空间中构造最优分离超平面。

需要映射和学习线性SVM：

• 把输入映射到特征空间F
• 在特征空间F中使用线性学习器分类

\[ f(x) = \sum_{i=1}^n\alpha_i^*y_i \color{red}{(\phi(x_i)\cdot \phi(x)}) + b^* \]

核函数的功能

核函数在特征空间中直接计算内积，就像在原始输入点的函数中一样，两个步骤合二为一： \[ K(x, z) = \phi(x) \cdot \phi(z) \] 分类函数： \[ f(x) = \sum_{i=1}^n\alpha_i^*y_i \color{red}{k(x_i, x)} + b^* \] 对偶问题： \[ \begin{align} & \max_\limits{\alpha} \; \sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j k(x_i, x) \\ & s.t, \quad \alpha_i \ge 0, \quad \sum_{i=1}^n \alpha_i y_i = 0 \end{align} \]

核函数处理非线性数据

简单例子

上面的数据线性不可分，两个维度(a, b)。 应该用二次曲线(特殊圆)来区分： \[ w_1a + w_2a^2 +w_3b + w_4b^2 + w_5ab + b=0 \] 看做映射到了五维空间： \[ w_1z_1 + w_2z_2 + w_3z_3 + w_4z_4 + w_5z_5 + b = \sum_{i=1}^5 w_iz_i + b = 0 \] 如下图：（实际映射到了三维空间的图），可以使用一个平面来分开：

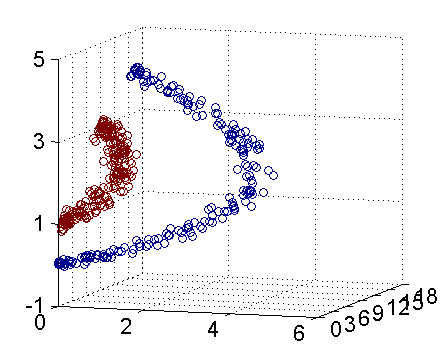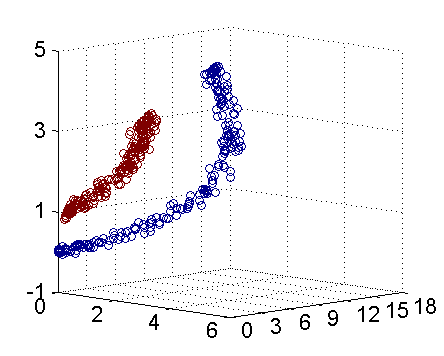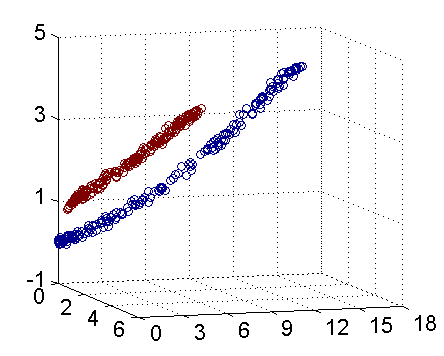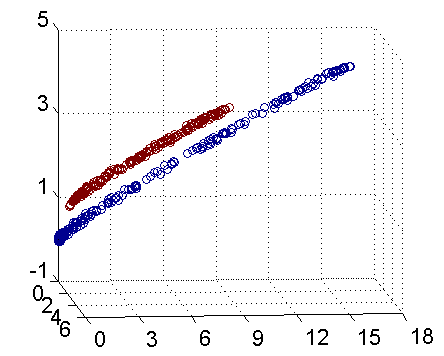
问题

五维是由1维和2维进行组合，就可以解决问题。所以对输入数据无脑组合映射到高维可以吗？当然是不可以的。维数太高，根本没法计算，不能无脑组合映射。

核函数的功能

看核函数： \[ k(x_1, x_2) = (x_1 \cdot x_2 + 1)^2 \] 核函数和上面映射空间的结果是一样的！区别：

• 映射计算：先映射到高维空间，然后根据内积进行计算
• 核函数：直接在原来的低维空间中计算，而不需显示写出映射后的结果。避开了在高维空间中的计算！

常用核函数

1 线性核 \[ k(x_1, x_2) = x_1 \cdot x_2 \quad\quad\text{(原始空间的内积)} \] 目的：映射前和映射后，形式上统一了起来。写个通用模板，再带入不同的核就可以了。

2 高斯核 \[ k(x_1, x_2) = \exp \left( - \frac{\|x_1 - x_2\|^2}{2\sigma^2}\right) \] 高斯核函数，非常灵活，应用很广泛。可以映射到无穷维。

\(\sigma\) 的选择

• 太大：权重衰减快，相当于映射到低维子空间
• 太小：将任意数据线性可分，容易陷入严重过拟合

3 多项式核 \[ k(x_1, x_2) = ((x_1, x_2) + R)^d \]

核函数总结

问题的出现

• 数据线性不可分，要映射到高维空间中去
• 不能无脑低维组合映射到高维空间，维度太大根本没法计算

核函数的功能

• 将特征向由低维向高维的转换
• 直接在低位空间中进行计算
• 实际的分类效果却是在高维上
• 避免了直接在高维空间中的复杂计算

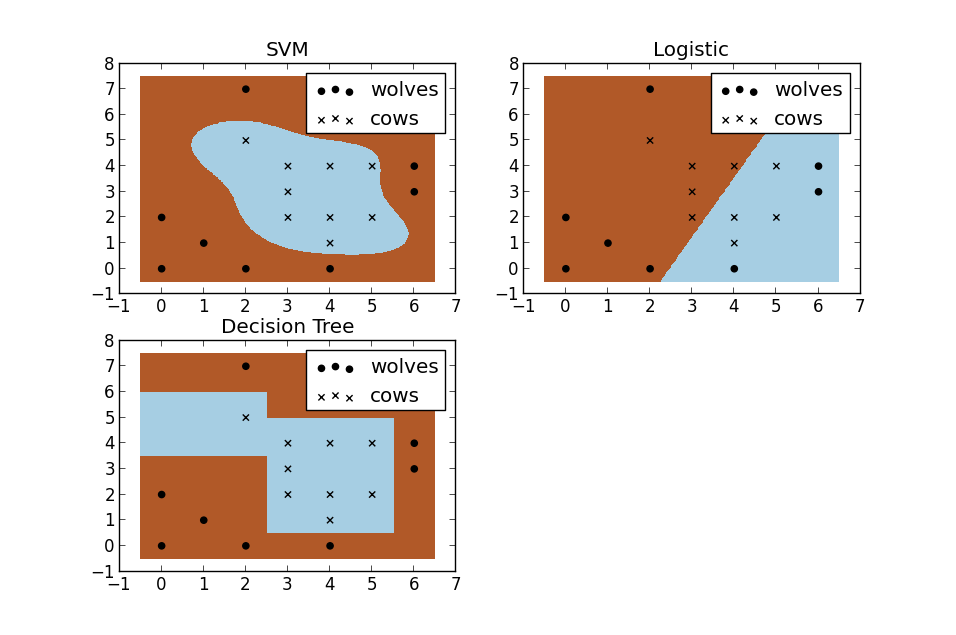
SVM曲线，逻辑回归和决策树是直线。SVM的效果好。

松弛变量软间隔最大化

定义

数据可能有一些噪声特异点outlier导致不是线性可分或者效果不好。 如果不处理outlier，则会非常影响SVM。因为本身支持向量就只有几个。

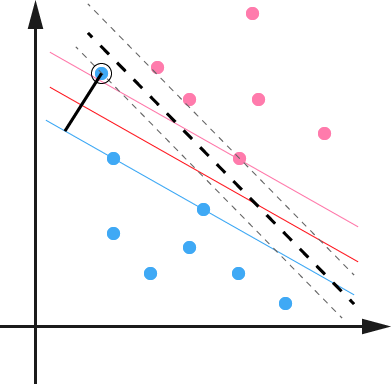
给每个数据点加上松弛变量\(\xi_i \ge 0\)， 使函数间隔+松弛变量大于等于1，即约束条件： \[ y_i(w \cdot x_i + b) \ge 1 - \xi_i, \quad \xi_i \ge 0 \] 为每个松弛变量\(\xi_i\)支付一个代价\(\xi_i\)， 新的目标函数和约束条件如下： \[ \min \frac{1}{2} \|w\|^2 + C\sum_{i=1}^n \xi_i \]

\[ s.t, \quad \quad y_i(w \cdot x_i + b) \ge 1 - \xi_i, \quad \xi_i \ge 0 \]

惩罚系数C是一个常数

• C大时，对误分类的惩罚增大
• C来调节权衡：使间隔尽量大；误分类点个数尽量少

求解

定义新的拉格朗日函数： \[ L(w,b,\xi,\alpha, r) = \frac{1}{2} \|w\|^2 + C\sum_{i=1}^n \xi_i -\sum_{i=1}^n \alpha_i \left(y_i(w^Tx_i+b) - 1 + \xi_i\right) - \sum_{i=1}^nr_i\xi_i \] 和前面对偶问题求解一样，求导求解： \[ \frac{\partial L}{\partial w} = 0 \quad \to \quad w = \sum_{i=1}^n\alpha_iy_ix_i \]

\[ \frac{\partial L}{\partial b} = 0 \quad \to \quad \sum_{i=1}^n\alpha_iy_i = 0 \]

\[ \frac{\partial L}{\partial \xi} = 0 \quad \to \quad C -\alpha_i - r_i = 0 \]

带入，得到新的L \[ \max_{\alpha} L = \sum_{i=1}^n\alpha_i -\frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_j( x_i \cdot x_j) \] 约束条件： \[ 0 \le \alpha_i \le C, \quad \sum_{i=1}^n \alpha_i y_i = 0 \]

SVM的深层理解

感知机算法

感知机算法是一个二类分类的线性模型，也是找一个超平面进行划分数据： \[ f(x) = \rm{sign}(w\cdot x + b) \] 损失函数是所有误分类点到超平面的总距离： \[ \min_\limits{w, b} L(w, b) = - \sum_{x_i \in M}y_i(w\cdot x_i + b) \] 可以使用SGD对损失函数进行优化。

当训练数据集线性可分时，感知机算法是收敛的。可以在一定迭代次数上，找到一个超平面，有很多个解。

感知机的超平面不是最优效果，最优是SVM。

损失函数

数据\(x\)， 预测值\(f(x)=\hat y\)， 真实值\(y\)。

常见损失

1. 01损失

\[ L(y, \hat y) = \begin{cases} 1, & y \neq \hat y \\ 0, & y = \hat y \end{cases} \]

2. 平方损失 \[ L(y, \hat y) = (y - \hat y)^ 2 \]

3. 绝对损失 \[ L(y, \hat y) = \vert y - \hat y\vert \]

4. 对数损失 \[ L(y, \hat y) = -\log P(y \hat x) \]

期望损失

期望损失也称为风险函数，需要知道联合概率分布\(P(X, Y)\)， 一般不知道。 \[ R_{\rm{exp}} = E_p[L(y, \hat y)] = \int_{(x,y)} L(y, \hat y) P(x, y) {\rm d}x{\rm d}y \] 经验损失

经验损失也成为经验风险 ，所以监督学习就是要经验风险最小化。 \[ R_{\rm emp}(f) = \frac{1}{N} \sum_{i=1}^NL(y_i, \hat y_i) \] 结构风险最小化

样本数量太小时，容易过拟合。需要加上正则化项，也称为惩罚项。 模型越复杂，越大。 \[ R_{\rm srm}(f) = \frac{1}{N} \sum_{i=1}^NL(y_i, \hat y_i) + \lambda J(f) \] \(\lambda\ge0\) 是系数，权衡经验风险和模型复杂度。 监督学习，就是要使结构风险最小化。

SVM也是最优化+损失最小。 可以从损失函数和优化算法角度去看SVM、boosting、LR，可能会有不同的收获。

SVM的合页损失函数

从最优化+损失最小的角度去理解SVM。

最小二乘法

最小二乘法，就是通过最小化误差的平方来进行数学优化。对参数进行求偏导，进行求解。

SMO

模型 \[ \min \frac{1}{2} \|w\|^2 + C\sum_{i=1}^n \xi_i \]

\[ s.t, \quad \quad y_i(w \cdot x_i + b) \ge 1 - \xi_i, \quad \xi_i \ge 0 \]

序列最小最优化SMO (Sequential minimal optimization)，解决求解\(\alpha\)的问题： \[ \min_{\alpha} L = \frac{1}{2}\sum_{i=1}^n\sum_{i=1}^n\alpha_i \alpha_j y_i y_jK(x_i, x_j) - \sum_{i=1}^n\alpha_i \]

\[ s.t, \quad \quad0 \le \alpha_i \le C, \quad \sum_{i=1}^n \alpha_i y_i = 0 \]

如果所有变量的解都满足KKT条件，则最优化问题的解已经得到。

思想

每次抽取两个乘子\(\alpha_1, \alpha_2\)，然后固定其他乘子，针对这两个变量构建一个子二次规划问题，进行求解。不断迭代求解子问题，最终解得原问题。

选择乘子

\(\alpha_1\)选择违反KKT条件最严重的，\(\alpha_2\)选择让\(\alpha_1\)变化最大的。