只是记录一下Co-Attention,后续再补上本篇论文的全部笔记吧。
论文:Hierarchical Question-Image Co-Attention for Visual Question Answering
我的相关笔记:Attention-based NMT阅读笔记和NLP中的Attention笔记
Co-Attention
这里以VQA里面的两个例子记录一下Co-Attention。即图片和问题。
注意力和协同注意力
注意力
注意力机制就像人带着问题去阅读, 先看问题,再去文本中有目标地阅读寻找答案。
机器阅读则是结合问题和文本的信息,生成一个关于文本段落各部分的注意力权重,再对文本信息进行加权。
注意力机制可以帮助我们更好地去捕捉段落中和问题相关的信息。
协同注意力
协同注意力是一种双向的注意力, 再利用注意力去生成文本和问句的注意力。
- 给文本生成注意力权值
- 给问句生成注意力权值
协同注意力分为两种方式:
- Parallel Co-Attention : 两种数据源A和B,先结合得到C,再基于结合信息C对A和B分别生成对应的Attention。
同时生成注意力 - Alternating Co-Attention: 先基于A产生B的attention,得到新的B;再基于新B去产生A的attention。两次
交替生成注意力
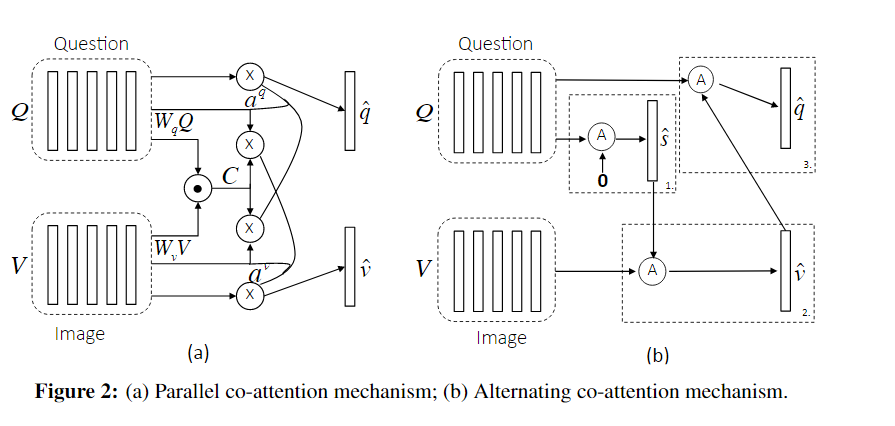
Parallel Co-Attention
图片特征:\(V \in \mathbb {R}^{d\times N}\) ,问句特征:\(Q \in \mathbb R^{d \times T}\) 。
同时生成图片和问题的注意力。
先计算关联矩阵: \[
C = \rm{tanh}(Q^T W_b V) \in \mathbb R^{T \times N}
\] 计算注意力权值 \(a^v\)和\(a^q\)
方法1:直接选择最大值。\(a^v_n = \max \limits_i(C_{i, n})\) ,\(a_t^q = \max \limits_i (C_{t, j})\)
方法2:把关联矩阵当做特征给到网络中,进行计算注意力权值,再进行softmax。更好 \[
H^v = \rm{tanh} (W_vV + (W_qQ)C), \quad \quad H^q = \rm{tanh} (W_qQ + (W_vV)C^T)
\]
\[ a^v = \rm{softmax}(w_{hv}^TH^v), \quad \quad a^q = \rm{softmax}(w^T_{hq}H^q) \]
利用注意力和原特征向量去计算新的特征向量 \[
\mathbf {\hat v} = \sum_{n=1}^N a^v_n \mathbf v_n, \quad \quad \mathbf { \hat q} = \sum_{t=1}^Tq_t^q \mathbf q_t
\]
Alternating Co-Attention

交替生成图片和问题的注意力。
- 把问题归纳成一个单独向量\(\mathbf {q}\)
- 基于\(\mathbf q\) 去和图片特征\(V\)去生成图像特征\(\mathbf {\hat v}\)
- 基于\(\mathbf v\)和问题特征\(Q\)去生成问题特征\(\mathbf {\hat q}\)
具体地,给一个\(X\)和attention guidance\(\mathbf g\) ,通过\(\mathbf {\hat x} = f(X, \mathbf g)\)去得到特征向量\(\mathbf {\hat x}\) \[
H = \rm {tanh} (W_x X+ (W_g \mathbf g) \mathbb 1^T)
\] \(\mathbf a ^x\) 是特征\(X\)的注意力权值 : \[
\mathbf a^x = \rm(softmax)(w^T_{hx} H)
\] 新的注意力向量 (attended image (or question) vector) : \[
\mathbf {\hat x} = \sum a_i^x \mathbf x_i
\] 对应本例子如下:
- \(X = Q, \; g = 0 \to \mathbf q\)
- \(X = V, \; g = \mathbf q \to \mathbf {\hat v}\)
- \(X = Q, \; g = \mathbf {\hat v} \to \mathbf {\hat q}\)
