leetcode题目

有序列表转二叉查找树-109

Convert Sorted List to Binary Search Tree

二叉树的最小深度-111

Minimum Depth of Binary Tree

最小深度：根节点到某个叶子节点的最短路径。

  • 为空，返回0
  • 左孩子为空，则结果在右孩子
  • 右孩子为空，则结果在左孩子
  • 左右均不为空，返回小的+1

二叉树遍历

先序遍历-144

Binary Tree Preorder Traversal

根、左、右。栈。

  • 先把根节点入栈
  • 栈不为空时，出栈一个元素
  • 访问该元素，右孩子进栈，左孩子进栈。 因为出栈，先出左孩子，再出右孩子。

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
vector<int> pre_order(TreeNode* root) {
    vector<int> vpre;
    stack<TreeNode*> st;
    if (root != nullptr) {
        st.push(root);
    }
    while (!st.empty()) {
        TreeNode* p = st.top();
        vpre.push_back(p->val);
        st.pop();
        // 右进、左进；出时：左先出
        if (p->right) {
            st.push(p->right);
        }
        if (p->left) {
            st.push(p->left);
        }
    }
    return vpre;
}

中序遍历-094

Binary Tree Inorder Traversal

思路

左、根、右。使用栈。

  1. p=root
  2. p不为空，p入栈，一直向左走p = p.left，扫描它的左孩子，所有左孩子依次入栈
  3. p为空时，p = st.top() ，p位于栈顶，显然没有左孩子或者左孩子已经遍历过，p访问出栈。
  4. 扫描右孩子 p = p.right

从根节点开始，一直向左，所有的左孩子入栈， 出栈一个节点，访问，它的右孩子入栈。

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> inorder_traversal(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> st;
    TreeNode* p = root;
    while (p || !st.empty()) {
        if (p) {
            // 根节点入栈
            st.push(p);
            // 扫描左孩子
            p = p->left;
        } else {
            // p位于栈顶，左孩子已经被遍历过或者没有左孩子，直接出栈访问
            p = st.top();
            res.push_back(p->val);
            st.pop();
            // 扫描右孩子
            p = p->right;
        }
    }
    return res;
}

后序遍历-145

Binary Tree Postorder Traversal

思路

左孩子、右孩子、根节点。使用栈。使用pre记录上一次遍历的节点。

  • 根节点入栈
  • 栈不为空，访问栈顶元素p
  • 直接访问p的条件：p没有左右孩子 or 左右孩子刚刚遍历结束，只要pre是左或者右孩子即可
  • p可以直接访问，则访问出栈
  • p不能直接访问，则左右孩子入栈

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
vector<int> post_order(TreeNode* root) {
    vector<int> res;
    stack<TreeNode*> st;
    // 前一次访问的节点
    TreeNode* pre = nullptr;
    if (root != nullptr) {
        st.push(root);
    }
    while (!st.empty()) {
        TreeNode* p = st.top();
        // 0. 检查是否可以直接访问p
        bool no_child = (p->left == nullptr && p->right == nullptr);
        bool pre_is_child = (pre == p->left || pre == p->right);
        if (nullptr == pre) {
            pre_is_child = false;
        }   
        // 1. p无左右子树 or 左右子树刚刚遍历完，直接访问p
        if (no_child || pre_is_child) {
            res.push_back(p->val);
            pre = p;
            st.pop();
        } 
        // 2. 需要将p的左右孩子入栈
        else {
            if (p->right) {
                st.push(p->right);
            }
            if (p->left) {
                st.push(p->left);
            }
        }
    }
    return res;
}

层次遍历-102

层次遍历，使用队列。

从上到下 Binary Tree Level Order Traversal 和从下到上 Binary Tree Level Order Traversal II。

如果只需要顺序放在一个数组里面，则不需要分层，直接层次遍历即可。

但是此题，需要分层构建vector。

数量记录思路

不是很好。

  • 队列层次遍历
  • 当前层在队列中的数量：cur_remain
  • 下一层的数量：next_level
  • cur_remain == 0时， 就切换到下一层

[关键代码]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
vector<vector<int>> levelOrder(TreeNode* root) {
    vector<vector<int>> res;
    if (root == nullptr) {
        return res;
    }
    queue<TreeNode*> q;
    q.push(root);
    res.push_back(vector<int>());
    // 当前层，在队列里面的元素数量
    int cur_remain = 1;
    // 下一层的元素数量
    int next_level = 0;
    while (!q.empty()) {
        TreeNode* now = q.front();
        q.pop();
        // 存入队列
        res[res.size() - 1].push_back(now->val);
        
        // 左右孩子入队
        if (now->left) {
            q.push(now->left);
            next_level++;
        }
        if (now->right) {
            q.push(now->right);
            next_level++;
        }
        // 当前层数量--
        cur_remain--;
        // 切换到下一层
        if (cur_remain == 0 && !q.empty()) {
            res.push_back(vector<int>());
            cur_remain = next_level;
            next_level = 0;
        }
    }
    return res;
}

一次遍历一层的思路

很好，掌握！

  • 一次while循环，保证当前队列里面只有当前层的元素，用vector记录当前层的序列
  • q.size() 获得当前层元素数量，然后本次循环，只从队列里面出这么多元素。
  • 依次遍历当前层的所有元素，出队，同时左右孩子入队
  • q为空，则所有层遍历结束
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
 * 保证当前队列的循环只有当前层的
 */
vector<vector<int>> level_order(TreeNode* root) {
    vector<vector<int>> res;
    if (root == nullptr) {
        return res;
    }
    queue<TreeNode*> q;
    q.push(root);
    // 一次while循环，出掉当前层的所有元素，下一层的元素全部入队
    while (!q.empty()) {
        // 当前层的数量和遍历结果序列
        int level_num = q.size();
        vector<int> curv;
        for (int i = 0; i < level_num; i++) {
            TreeNode* p = q.front();
            // p的左右孩子入队列
            if (p->left) q.push(p->left);
            if (p->right) q.push(p->right);
            // p出队，放到当前层的vector中
            q.pop();
            curv.push_back(p->val);
        }
        // 放到末尾，就是从下到上
        // res.insert(res.begin(), curv); 
        res.push_back(curv);
    }
    return res;
}

发现重复的数字-287

Find the Duplicate Number， 类似于aim2offer中查找重复的数字

数组a，有n+1个数，都在[1,n]范围内，只有一个重复的元素。找到它

二分思路

[1, n]这个范围有n个数。划分为两个范围[1, m]和[m+1, n]

  • 每次去遍历整个数组，统计两个范围内的数字的数目
  • 统计整个数组中元素在[1, m]范围内的个数\(c_1\)
  • 统计整个数组中元素在[m+1, n]范围内的个数\(c_2\)

[1, m]这m个数字的数量是c

  • 如果 c > m， 则1, m]内一定存在重复的数，e = m
  • 否则，[m+1, n]一定存在重复的数，s = m + 1

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*
 * 找到一个重复的数字
 * Args:
 *      a -- 数组，n+1个元素，范围[1,n]，至少有一个重复的数字
 * Returns:
 *      dup -- 重复的数字
 */
int find_duplicate(const vector<int>& a) {
    int n = a.size() - 1;
    if (n <= 0) {
        return 0;
    }
    int l = 1;
    int r = n;
    int dup = -1;
    // 不断缩小范围
    while (l <= r) {
        int m = (l + r) >> 1;
        // 统计[l,m]在a中的出现次数
        int count = count_range(a, l, m);
        if (l == r) {
            if (count >= 2) {
                dup = l;
                break;
            }
        }
        
        // [l, m]有重复的
        if (count > (m - l + 1)) {
            r = m;
        } 
        // [m+1, r]有重复的
        else {
            l = m + 1;
        }
    }
    return dup;
}

/*
 * 找到数组a中，[min, max]这些数的出现次数
 */
int count_range(const vector<int>& a, int min, int max) {
    int count = 0;
    for (int i = 0; i < a.size(); i++) {
        if (a[i] >= min && a[i] <= max) {
            count++;
        }
    }
    return count;
}

合并两条有序链表-021

Merge Two Sorted Lists ，和归并排序的Merge操作 很类似。

考虑鲁棒性

思路

  • \(l_1\)与\(l_2\)若有一个为空的，则返回另一个
  • 初始化新的head，选择\(l_1\)与\(l_2\)中第一个节点较小的那个
  • while循环，谁小选谁
  • 结束之后，直接把未空的链表链接上即可

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
    if (l1 == nullptr) {
        return l2;
    }
    if (l2 == nullptr) {
        return l1;
    }
    
    // 初始化head
    ListNode* head = nullptr;
    if (l1->val < l2->val) {
        head = l1;
        l1 = l1->next;
    } else {
        head = l2;
        l2 = l2->next;
    }
    
    // 遍历两条链表，每次选择小的追加到p的后面
    ListNode* p = head;
    while (l1 && l2) {
        if (l1->val < l2->val) {
            p->next = l1;
            l1 = l1->next;
        } else {
            p->next = l2;
            l2 = l2->next;
        }
        p = p->next;
    }
    // 某一条链表还有剩余
    if (l1) {
        p->next = l1;
    }
    if (l2) {
        p->next = l2;
    }
    return head;
}

合并多条有序链表-023

Merge k Sorted Lists

我们已经会合并2条链表了，可以使用归并排序和二分查找的思想来合并多个列表。

示例

现在有1, 2, 3, 4, 5, 6条链表

  • 第一步：1-6，2-5，3-4合并，得到新的1, 2, 3
  • 第二步：1-3合并，2不动，得到新的1, 2
  • 第三步：1-2合并， 得到新的2， 合并完成
  • 返回list[0]

总结

  1. 直到len==1 合并到只有一条链表，合并到list[0]
  2. 对于当前len，折半两两合并，i和len-i-1合并，放到前面lists[i]
  3. len缩减一半，len=(len+1)/2

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
ListNode* mergeKLists(vector<ListNode*>& lists) {
	if (lists.empty()) {
      	return nullptr;
    }
    int len = lists.size();
  	// 直到只有一条链表
    while (len > 1) {
      	// 依次合并前后两条链表
    	for (int i = 0; i < len / 2; i++) {
          	// 合并放到list[i]
        	lists[i] = mergeTwoLists(lists[i], lists[len - i - 1]);
      	}
      	len = (len + 1) / 2;
    }
    return lists[0];
}

Z型打印二叉树-103

Binary Tree Zigzag Level Order Traversal

参考层次遍历 一次遍历一层的思路。

  • 一次遍历一层，得到当前层的遍历结果
  • 单数，从左向右；偶数，从右向左
  • 每次遍历一个元素，把左右孩子入队

  • 根节点，向右走
  • 第二层，向左走
  • 向右走，从队头出，孩子先左后右，加到队尾
  • 向左走，从队尾出，孩子先右后左，加到队首

两个栈的思路

栈1初始存放根节点，栈2为空

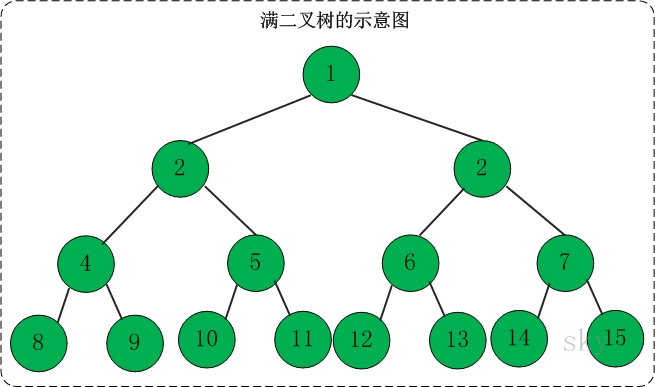
  • 向右走，栈1全部出栈，先左后右孩子依次压入栈2，栈底-栈顶，栈2为2 3
  • 向左走，栈2全部出栈，先右后左孩子依次压入栈1，栈1为7 6 5 4
  • 向右走，栈1出栈，左右孩子依次压入栈2，栈2为8 9 10 11 12 13 14 15
  • 向左走，栈2出栈，结束

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
 * 使用两个栈z型层次打印二叉树
 */
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
    vector<vector<int>> res;
    if (root == nullptr) {
        return res;
    }

    stack<TreeNode*> st1;
    stack<TreeNode*> st2;

    st1.push(root);

    while (!st1.empty() || !st2.empty()) {
        // 向右走
        vector<int> curv;
        if (!st1.empty()) {
            while (!st1.empty()) {
                TreeNode* p = st1.top();
                st1.pop();
                curv.push_back(p->val);
                if (p->left) st2.push(p->left);
                if (p->right) st2.push(p->right);
            }
            
        } 
        // 向左走
        else {
            while (!st2.empty()) {
                TreeNode* p = st2.top();
                st2.pop();
                curv.push_back(p->val);
                if (p->right) st1.push(p->right);
                if (p->left) st1.push(p->left);
            }
        }
        res.push_back(curv);
    }
    return res;
}

二叉树路径求和-112.113.437

题目1 从根节点到叶子求和-112

Path Sum， EASY

给一颗二叉树和一个sum值，判断是否有从根节点到叶子节点的路径，使得路径上的节点求和等于sum

思路

做减法

  • 根节点为空，False
  • 没有孩子，判断root.val == sum
  • 有孩子，把sum减掉根节点的值，去判断左右子树是否有 ，sum = sum - root.val

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
bool hasPathSum(TreeNode* root, int sum) {
    // 1. 节点为空
    if (root == nullptr) {
        return false;
    }
    // 2. 没有左右子树，直接判断
    if (!root->left && !root->right) {
        return root->val == sum;
    }
    // 3. 减小sum，去递归判断左右子树
    int newsum = sum - root->val;
    return hasPathSum(root->left, newsum) || hasPathSum(root->right, newsum);
}

题目2 从根节点到叶子节点求和-保存路径-113

Path Sum-113， Medium

给二叉树和sum值，找到root-to-leaf的路径，使得和为sum。保存该路径

思路

用vector<int> path 来记录当前路径， vector<vector<int>> res 记录最终结果

  • 根节点为空，返回
  • 到达叶子节点，val == sum， 把当前节点加入path，当前path加入res， 否则返回
  • 非叶子节点，把当前节点加入path，去左右子树中遍历，继续追加path直到叶子节点
  • 非叶子节点，结束后，把当前节点从path中删除

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
/*
 * 找到树种从root到leaf的所有和为sum的路径
 */
vector<vector<int>> pathSum(TreeNode* root, int sum) {
    vector<vector<int>> res;
    if (root == nullptr) {
        return res;
    }
    vector<int> path;
    find_path(root, sum, path, res);
    return res;
}

/*
 * 递归遍历节点，逐渐添加节点到当前的path，叶子节点，满足要求时，则把path追加到res中
 * Args:
 *      root -- 当前节点
 *      path -- 当前路径
 *      res -- 所有路径
 * Returns:
 *      None
 */
void find_path(TreeNode* root, int sum, vector<int>& path, vector<vector<int>> &res) {
    if (root == nullptr) {
        return;
    }
    // 到达叶子节点
    if (!root->left && !root->right) {
        if (root->val == sum) {
            path.push_back(root->val);
            res.push_back(path);
            path.pop_back();
        }
        return;
    }

    // 当前节点加到path中
    path.push_back(root->val);

    // 更新sum，到左右子树中去添加path
    int newsum = sum - root->val;
    if (root->left) {
        find_path(root->left, newsum, path, res);
    }
    if (root->right) {
        find_path(root->right, newsum, path, res);
    }
    // 当前节点从path中移除
    path.pop_back();
}

题目3 求二叉树的所有和为sum的路径，任意起始节点-437

给一颗二叉树和sum，求出所有和为sum的路径数量，从任意节点开始和结束。

思路

  • 层次遍历，以每一颗节点为起始值，找到以它开始的路径数量
  • 节点为空，0
  • 无孩子，不相等，0
  • 无孩子，相等，1
  • 有孩子，相等，c = 1， 不相等c = 0。 更新sum，继续递归查找左右孩子的count。返回c+count

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
/*
 * 找到树中，和为sum的所有路径数量
 */
int pathSum(TreeNode* root, int sum) {
    if (root == nullptr) {
        return 0;
    }
    queue<TreeNode*> q;
    q.push(root);
    int count = 0;
    // 前序遍历
    while (!q.empty()) {
        TreeNode* now = q.front();
        q.pop();
        count += count_from_root(now, sum);
        if (now->left) q.push(now->left);
        if (now->right) q.push(now->right);
    }
    return count;
}

/*
 * 以root为起始节点，向下走，和为sum的路径的条数
 */
int count_from_root(TreeNode* root, int sum) {
    // 空
    if (root == nullptr) return 0;
    // 直接根节点就满足，无需看孩子
    int c = 0;
    if (sum == root->val) {
        // 相等
        c = 1;
    } else if (!root->left && !root->right) {
        // 无孩子，不相等
        return 0;
    }
    // c+左右孩子的
    int newsum = sum - root->val;
    return c + count_from_root(root->left, newsum) + count_from_root(root->right, newsum);
}

有序链表转平衡BST-109

Convert Sorted List to Binary Search Tree， Medium。 类似题型：BST转有序双向链表

给一个有序链表，转化为平衡的二叉搜索树

思路

有序 -- BST的中序遍历；平衡 -- 以中间节点为根节点，分为左右子树递归去创建。

  • 计算总结点数量 -- size， 递归去构建树go(0, size - 1)
  • go(head, start, end) ，计算出中间节点mid-node， 构造树根root
  • 左孩子root.left = go(head, start, mid-1)， 右孩子root.right = go(now.next, mid+1, end)
  • 返回当前树根节点root

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
/*
 * 把有序链表转化为平衡的BST
 * Args:
 *      head -- 链表
 * Returns:
 *      root -- 树的头结点
 */ 
TreeNode* sortedListToBST(ListNode* head) {
    if (head == nullptr) {
        return nullptr;
    }

    int size = 0;
    ListNode* p = head;
    while (p) {
        ++size;
        p = p->next;
    }
    
    return create_tree(head, 1, size);
}

/*
 * 递归中序创建树
 * Args:
 *      head -- 链表头节点
 *      start -- 起始节点编号，从1开始
 *      end -- 结束节点编号
 * Returns:
 *      root -- 树的根节点
 */
TreeNode* create_tree(ListNode* head, int start, int end) {
    // 0. 递归终止条件
    if (head == nullptr || start > end) {
        return nullptr;
    }
    
    // 1. 找到中间节点，构建根节点
    int mid = (end + start) / 2;
    ListNode* node = head;
    for (int i = start + 1; i <= mid; i++) {
        node = node->next;
    }
    TreeNode* root = new TreeNode(node->val);

    // 2. 递归构造左右子树
    root->left = create_tree(head, start, mid - 1);
    root->right = create_tree(node->next, mid + 1, end);
    
  return root;
}

序列化二叉树-297

Serialize and Deserialize Binary Tree， Hard

把二叉树序列化为字符串，把字符串反序列化为一棵树

思路

前序遍历来保存序列，保存成一颗完全二叉树，空节点用$表示，使用空格进行分割。

序列化

  • 序列化为一颗完全二叉树，先序递归。遇到空指针，则用$代替
  • 先把字符放到stringstream里面，<<输入， 最后s.str()得到字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/*
 * 把一棵树序列化为一个字符串，前序完全二叉树序列
 * Args:
 *      root -- 树
 * Returns:
 *      str -- 序列化后的字符串
 */
string serialize(TreeNode* root) {
    if (root == nullptr) {
        return "";
    }
    stringstream buf;
    build_string(root, buf);
    return buf.str();
}

/*
 * 递归把二叉树序列化到buf字符串中
 * Args:
 *      root -- 当前的根节点
 *      buf -- 字符串buffer
 * Returns:
 *      None，都写到了buf中
 */
void build_string(TreeNode* root, stringstream& buf) {
    if (root == nullptr) {
        buf << "$" << " ";
        return;
    }
    buf << root->val << " ";
    build_string(root->left, buf);
    build_string(root->right, buf);
    return;
}

从字符串中解析得到序列，存到队列中

1
2
3
4
5
6
7
8
9
10
11
12
/*
 * 分割字符串，把字符写到容器q里面
 */
void split(const string& str, queue<string> &q, const char delim = ' ') {
    istringstream input;
    input.str(str);
    string line;
    while (std::getline(input, line, delim)) {
        q.push(line);
    }
    return;
}

反序列化

得到队列序列之后，可以对其进行递归反序列化构建树。先序序列，不是层次序列。

  • 根-左-右，队列。出队，建立根节点
  • 左-右，队列，递归建立左孩子
  • 右，队列，建立右孩子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/*
 * 把String解析为一棵树
 * Args:
 *      data -- 序列化后的字符串
 * Returns:
 *      root -- 树
 */
TreeNode* deserialize(const string& data) {
    if (data.empty()) {
        return nullptr;
    }
    // 先序序列
    queue<string> preorder;
    split(data, preorder);

    return build_tree(preorder);
}

/*
 * 递归先序构造树
 * Args:
 *      prev -- 先序遍历序列
 * Retursn:
 *      root -- prev[i]为根构建的树
 */
TreeNode* build_tree(queue<string>& pres) {
    if (pres.size() == 0) {
        return nullptr;
    }

    string val = pres.front();
    pres.pop();

    // 当前为空节点
    if (val == "$") {
        return nullptr;
    }

    // 有值
    TreeNode* root = new TreeNode(std::stoi(val));

    // 递归按照顺序构建左右子树
    root->left = build_tree(pres);
    root->right = build_tree(pres);

    return root;
}

数字全排列-046

Permutations, Medium。 搜索树

给一个数组，返回全排列。每个数字都不相同

思路

全排列回溯法搜索。一个数组，搜索第t层的时候

  • 前面t-1层都已经ok
  • 遍历后面的所有元素，给到t层，去搜索
  • 每次进行交换

github代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
 * 数组的全排列
 */
vector<vector<int>> permute(vector<int> &nums) {
    vector<vector<int>> res;
    dfs(nums, 0, res);
    return res;
}

/*
 * 回溯搜索排列树，遍历当前第i层的所有可能性，前面i-1已经全部确定好
 * Args:
 *      t -- 第几层，[0, n-1]
 *      path -- 当前路径，[0,i-1]已经确定好，[i,n-1]是剩余的数字，遍历每一种可能给到i
 *      res -- 总的结果
 * Returns:
 *      None
 */
void dfs(vector<int>& path, int t, vector<vector<int>>& res) {
    if (t >= path.size()) {
        res.push_back(path);
        return;
    }
    
    for (int i = t; i < path.size(); i++) {
        std::swap(path[t], path[i]);
        dfs(path, t + 1, res);
        std::swap(path[t], path[i]);
    }
}

重复数字全排列-047

重复数字全排列-047

给一个数组，里面有一些重复的数字，给出所有的排列可能

思路

重复的原因：当为t设置值的时候，遍历后面的所有元素给t赋值，但是后面都有一些重复的数值。

比如说 1 2 1 1， 开始是1，1会与最后的两个1再进行交换，然而其实是一样的。没必要了。

每次遍历交换的时候，只交换遍历后面不重复的元素。

github代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/*
 * 回溯搜索排列树，遍历当前第i层的所有可能性，前面i-1已经全部确定好
 * Args:
 *      t -- 第几层，[0, n-1]
 *      path -- 当前路径，[0,i-1]已经确定好，[i,n-1]是剩余的数字，遍历每一种可能给到i
 *      res -- 总的结果
 * Returns:
 *      None
 */
void dfs(vector<int>& path, int t, vector<vector<int>>& res) {
    if (t >= path.size()) {
        res.push_back(path);
        return;
    }
    // 不重复的元素与其索引
    set<int> vals;
    set<int> idx;
    for (int i = t; i < path.size(); i++) {
        if (vals.find(path[i]) == vals.end()) {
            vals.insert(path[i]);
            idx.insert(i);
        }
    }

    for_each(idx.begin(), idx.end(), [&](int i) {
       std::swap(path[t], path[i]);
        dfs(path, t + 1, res);
        std::swap(path[t], path[i]);
    });
}

组合问题

给n个字符，要组成m个字符，问有多少种组成方法

有点类似于01背包的选择。

  • 选择第一个字符，则在后面选择m-1个字符
  • 不选择第一个字符，则在后面选择m个字符

正方体顶点和相等问题

给8个数字，正方体有8个顶点，数字放在顶点上。使得3对对面的顶点和相等。

也就是搜索，然后限定一些条件。

8皇后问题

8*8的象棋摆8个皇后，任意两个皇后不能在同一行、同一列或同一对角线上。问有多少种摆法

N皇后问题-051

n*n的棋盘摆n个皇后，任意两个皇后不能在同一行、同一列或同一对角线上。返回摆法。

N-Queens

  • 每一行一个皇后，每一行有n个选择。就去dfs搜索所有的排列树。
  • path[t]=k， 第t行的皇后在第k列
  • k不能在前面皇后的：同一列、主对角线、副对角线 。别忘记副对角线。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
/*
 * 返回n皇后的解法
 */
vector<vector<string>> solveNQueens(int n) {
    // 1. 获得所有可能的位置
    vector<vector<int>> locations;
    vector<int> path(n);
    std::iota(path.begin(), path.end(), 0);
    dfs(0, n, path, locations);
    
    // 2. 构造返回结果
    vector<vector<string>> res;
    for (auto loc : locations) {
        vector<string> solu;
        for (int i : loc) {
            string line(n, '.');
            line[i] = 'Q';
            solu.push_back(line);
        }
        res.push_back(solu);
    }
    show(res[0]);
    
    return res;
}

/*
 * dfs，设置t行的皇后位置
 * Args:
 *      t -- 第t行，从0开始
 *      n -- n皇后
 *      path -- 当前的路径方案
 *      res -- 总的方案
 * Returns:
 *      None
 */
void dfs(int t, int n, vector<int>& path, vector<vector<int>>& res) {
    if (t == n) {
        res.push_back(path);
        return;
    }
    // 前面t-1行已经ok，再后面的t-n个选择中选择遍历t
    for (int i = t; i < n; i++) {
        if (legal(t, path[i], path) == true) {
            swap(path[i], path[t]);
            //cout << "t=" << t << ", k=" << path[i] << endl;
            //for_each(path.begin(), path.end(), [](int i){cout << i << " ";});
            dfs(t + 1, n, path, res);
            swap(path[i], path[t]);
        }
    }
}

/*
 * 合法性判断，同一列、主对角线、副对角线
 * Args:
 *      t -- 第t行，从0开始
 *      k -- 放在第k个列，从0开始
 *      path -- 当前的路径，[0,t-1]行已经放好
 * Returns:
 *      true or false
 */
bool legal(int t, int k, const vector<int>& path) {
    for (int i = 0; i <= t - 1; i++) {
        // 1. 不能和之前的在同一列
        if (path[i] == k) {
            return false;
        }
        // 2. 不能在主对角线上
        if (t - i == k - path[i]) {
            return false;
        }
        
        // 3. 不能在副对角线上
        if (t + k == i + path[i]) {
            return false;
        }

        printf("p[%d]=%d,p[%d]=%d\n", t, k, i, path[i]);
    }
    return true;
}

N皇后问题-052

返回有多少种解法

做了上面的题，那这个就很简单了，返回数量就行了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
 * 返回n皇后的解法
 */
int solveNQueens(int n) {
    // 所有的结果
    vector<vector<int>> locations;
    // 当前的位置
    vector<int> path(n);
    // 初始化为0-n-1
    std::iota(path.begin(), path.end(), 0);
    // dfs遍历搜索
    dfs(0, n, path, locations);
    return locations.size();
}

查找第k大的数总结

给N个数，确定第k个最大值

1 排序

排好序，取出第k大的值。\(O(n\log n + k)\)

2 简单选择排序

简单选择。第k次选择，就是第k大的数字。\(O(n*k)\)

3 快速排序思想

每次partition，会把x放到位置i上。注意partition要从大到小排列，左大右小，而不是普通排序的左小右大。

  • i == k， 则就是a[i]
  • k > i， 则在i的右边
  • k < i， 则在i的左边

[关键代码]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
 * 使用快排思想查找第k大的数字，从大到小排列！！
 * Args:
 *      a -- 数组
 *      l -- 范围的开始
 *      r -- 范围的结束
 *      k -- 该范围内第k大的数
 * Returns:
 *      第k大的数
 */
int find_kth_num(vector<int> &a, int l, int r, int k) {
    // 1. 划分。左边大，中间a[l]，右边小
    int i = partition(a, l, r);
    // 2. 通过i+1==k来判断是否是第k大的数
    if (i + 1 == k) {
        return a[i];
    } else if (i + 1 > k) {
        // 在左边
        return find_kth_num(a, l, i - 1, k);
    } else {
        // 在右边
        return find_kth_num(a, i + 1, r, k);
    }
}

4 最大堆

\(O(4*n)\)的空间建立最大堆，pop k次即可。\(O(4 \times n + k\times\log n)\)

5 最小堆

维护大小为k的最小堆，遍历数组

  • 堆顶元素大，则不管
  • 堆顶元素小，则把当前值插入堆中
  • 最后的堆顶，就是第k大的元素

\(O(n \times \log k)\)

6 Hash法

查找最小的k个数的总结

给一个数组，找到最小的k个数。注意改变或不改变原数组

1 排序思路

对n个数字从小到大排好序，再取前k个数。O(nlogn + k)=O(nlogn) 。排序算法总结

2 快速排序

排好前k个即可，改变原数组。

3 最大堆

建立大小为k的最大堆。不改变原数组。遇到新的元素，小于堆顶，则加入

4 堆排序

对整个数组n进行堆排序，每次取堆顶，取k次。

数组中次数超过一半的数-169

Majority Element-169， easy

一个数组，有一个元素出现次数超过一半，找到它。

思路0 先排序再找

\(O(n\log n)\)

思路1 快速排序查找第k大元素思想

快速排序笔记 。

  • 如果排好序，则该重复的数字应该在数组中间\(a_{\frac{n}{2}}\)。 也就是中位数，第n/2大的数字
  • 问题就转化为查找数组中的K大的元素

查找第k大的元素

  • partition(a, l, r) 会把x=a[l]放到中间去，小于的在右边，大于的在左边。返回x的最终位置i
  • i == k， 则x就是第k大的元素
  • k < i， 则k在右边
  • k > i， 则k在左边
  • 继续查找，知道 i == k

思路2 count加加减减思想

  • 遇见友军（相同的），就++
  • 遇见敌军（不同的），就--
  • 最后剩余的肯定就是人数最多的那个（数字）

[关键代码]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
 * 查找主元素，阵地攻守思想。相同加价，不同减减，为0重新赋值
 */
int majority_element(vector<int>& a) {
    if (a.size() == 0) {
        return 0;
    }
    // 当前数值与计数
    int res = a[0];
    int count = 1;
    for (int i = 1; i < a.size(); i++) {
        if (a[i] == res) {
            // 相同++
            count++;
        } else {
            // 不同--或者重置为1
            if (count == 0) {
                res = a[i];
                count = 1;
            } else {
                count--;
            }
        }
    }
    return res;
}

主元素2-229

给一个数组，找到所有出现次数超过n/3的数

Majority Element II, medium 。

思路

当然最终结果只有2个或1个。思路同阵地攻守。

  • 用两个变量去记录两个主元素
  • 有一个相同，对应加1
  • 两个都不同，有一个count==0， 则重置
  • 两个都不听，两个都有count，则都减减
  • 遍历之后，得到两个数，两个count
  • 返回count > n/3的数

最后，一定要注意去重！n1 != n2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
/*
 * 查找出现次数超过n/3的元素
 * Args:
 *      nums -- 数组
 * Returns:
 *      res -- 超过n/3的元素
 */
vector<int> majority_element(const vector<int>& nums) {
    vector<int> res;
    if (nums.empty()) {
        return res;
    }
    
    // 1. 找到出现次数最多的两个数
    int n1 = 0, c1 = 0;
    int n2 = 0, c2 = 0;

    for (int n : nums) {
        if (n == n1) {
            c1++;
        } else if (n == n2) {
            c2++;
        } else if (c1 == 0) {
            n1 = n;
            c1 = 1;
        } else if (c2 == 0) {
            n2 = n;
            c2 = 1;
        } else {
            c1--;
            c2--;
        }
    }

    c1 = 0, c2 = 0;
    // 2. 重新计算出现次数
    for (auto n : nums) {
        if (n1 == n) {
            c1++;
        } else if (n2 == n) {
            c2++;
        }
    }

    // 3. 把出现次数超过n/3的数字放到res里面
    if (c1 > nums.size() / 3) {
        res.push_back(n1);
    }
    // 去重
    if (n2 != n1 && c2 > nums.size() / 3) {
        res.push_back(n2);
    }

    return res;
}

最长不重复子字符串-003

Longest Substring Without Repeating Characters-003

给一个字符串，找到里面最长子字符串的长度。

1 DP思路

设l[i]=k， 是以s[i]结尾最长字符串的长度是k。从左到右进行计算。遍历到s[i]

1、 s[i]在前面没有出现过，l[i] = l[i-1] + 1

2 、s[i]在前面出现过，计算该字符现在与前面两次出现的距离d，比较d和s[i-1]的最大长度l[i-1]

  • d > l[i-1]， d很远（不在i-1的最长字符串里），l[i] = l[i-1] + 1
  • d <= l[i-1]，d很近（在i-1的最长字符串里），l[i]=d

使用HashMap<Char, Int>去记录位置信息，保留最近时间的出现位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
 * 字符串中，最长不重复子串的长度，是连续
 * Args:
 *      s -- 原字符串
 * Returns:
 *      len -- 最长子串长度
 */
int long_substr_len(const string& s) {
    if (s.empty()) {
        return 0;
    }
    // 长度，l[i]=k，以s[i]结尾的最大子串长度为k
    vector<int> l(s.length(), 0);
    // 位置，m['a']=i，最近，字符a出现的位置是i
    map<char, int> m;
    for (int i = 0; i < s.length(); i++) {
        char ch = s[i];
        if (i == 0) {
            l[i] = 1;
            m[ch] == i;
            continue;
        }
        if (m.find(ch) == m.end()) {
            // ch 没出现过
            l[i] = l[i-1] + 1;
        } else {
            // ch 出现过，距离比较
            int d = i - m[ch];
            if (d > l[i-1]) {
                // 上一个ch距离很远
                l[i] = l[i-1] + 1;
            } else {
                // 上一个ch距离很近
                l[i] = d;
            }
        }
        // 更新出现位置
        m[ch] = i;
    }
    return *max_element(l.begin(), l.end());
}

丑数-263-264-313

263-判断是否是丑数 ，easy

只包含2、3、5作为因子的正整数是丑数，1也是。判断是否是丑数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
bool isUgly(int num) {
    // 特殊情况
    if (num <= 0) {
        return false;
    }
    if (num == 1) {
        return true;
    }
    // 不断分解2,3,5
    vector<int> a = {2, 3, 5};
    for (auto i : a) {
        while (num % i == 0) {
            num /= i;
        }
    }
    return num == 1;
}

264-找到第n个丑数 ，medium

找到第n个丑数

如果依次找，所有的数都要分解求余，效率低。**丑数=丑数*{2,3,5}。 用数组去存放丑数，从1开始依次向前面递推计算。**

用3个索引，去分别保存乘以2,3,5的基数，每次选择最小的作为下一个丑数，同时更新对应的索引++。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
 * 第n个丑数，从已有的丑数不断地向前乘得到新的丑数。
 */
int nthUglyNumber(int n) {
    if (n <= 0) {
        return -1;
    }
    if (n == 1) {
        return 1;
    }
    
    vector<int> u(n);
    u[0] = 1;
    int t2 = 0, t3 = 0, t5 = 0;
    // 计算丑数
    for (int i = 1; i < n; i++) {
        // 计算新的丑数，选择最小的
        int cur = min(min(u[t2] * 2, u[t3] * 3), u[t5]*5);
        u[i] = cur;
        // 更新基数索引
        if (cur == u[t2] * 2) {
            t2++;
        }
        if (cur == u[t3] * 3) {
            t3++;
        }
        if (cur == u[t5] * 5) {
            t5++;
        }
    }
    return u[n-1];
}

313-超级丑数， medium

超级丑数是，给一个素数列表去计算丑数，不再局限于2,3,5去计算丑数。

给一个素数列表和n，返回第n个丑数

和上一个思路一致，用数组保存。注意t数组的初始大小是primes.size()，而不是n。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/*
 * 给定素数，返回第n个丑数
 */
int nthSuperUglyNumber(int n, vector<int>& primes) {
    if (n == 1) {
        return 1;
    }
    
    if (n <= 0 || primes.empty()) {
        return -1;
    }
    
    vector<int> u(n);
    u[0] = 1;
    vector<int> t(primes.size(), 0);
    
    for (int i = 1; i < n; ++i) {
        // 计算新的丑数，选择最小的
        int cur = INT_MAX;
        for (int j = 0; j < primes.size(); ++j) {
            cur = min(cur, u[t[j]] * primes[j]);
        }
        u[i] = cur;
        // 更新索引，向前推进
        for (int j = 0; j < primes.size(); ++j) {
            if (cur == u[t[j]] * primes[j]) {
                t[j]++;
            }
        }
    }
    return u[n-1];
}