cs224n的第一个作业，包括softmax、神经网络基础和词向量

Softmax

Softmax常数不变性

\[ \rm{softmax}(\mathbf{x})_i = \frac{e^{\mathbf x_i}}{\sum_{j}e^{\mathbf{x}_j}} \]

一般在计算softmax的时候，避免太大的数，要加一个常数。 一般是减去最大的数。 \[ \rm{softmax}(x) = \rm{softmax}(x+c) \]

关键代码

1
2
3
4
5
6
7
8
def softmax(x):
    exp_func = lambda x: np.exp(x - np.max(x))
    sum_func = lambda x: 1.0 / np.sum(x)
    x = np.apply_along_axis(exp_func, -1, x)
    denom = np.apply_along_axis(sum_func, -1, x)
    denom = denom[..., np.newaxis]
    x = x * denom
   	return x

神经网络基础

Sigmoid实现

我的sigmoid笔记 \[ \begin{align} & \sigma (z) = \frac {1} {1 + \exp(-z)}, \; \sigma(z) \in (0,1) \\ \\ & \sigma^\prime (z) = \sigma(z) (1 - \sigma(z)) \\ \end{align} \] 关键代码

1
2
3
4
5
6
7
8
9
10
def sigmoid(x):
    s = 1.0 / (1 + np.exp(-x))
    return s


def sigmoid_grad(s):
    """ 对sigmoid的函数值，求梯度
    """
    ds = s * (1 - s)
    return ds

Softmax求梯度

交叉熵和softmax如下，记softmax的输入为\(\theta\) ，\(y\)是真实one-hot向量。 \[ \begin{align} & \rm{CE}(y, \hat y) = - \sum_{i} y_i \times \log (\hat y_i) \\ \\ & \hat y = \rm{softmax} (\theta)\\ \end{align} \] softmax求导

引入记号： \[ \begin{align} & f_i = e^{\theta_i} & \text{分子} \\ & g_i = \sum_{k=1}^{K}e^{\theta_k} & \text{分母，与i无关} \\ & \hat y_i = S_i = \frac{f_i}{g_i} & \text{softmax}\\ \end{align} \] 则有\(S_i​\)对其中的一个数据\(\theta_j​\) 求梯度： \[ \frac{\partial S_i}{\partial \theta_j} = \frac{f_i^{\prime} g_i - f_i g_i^{\prime}}{g_i^2} \] 其中两个导数 \[ f^{\prime}_i(\theta_j) = \begin{cases} & e^{\theta_j}, & i = j\\ & 0, & i \ne j \\ \end{cases} \]

\[ g^{\prime}_i(\theta_j) = e^{\theta_j} \]

\(i=j\)时 \[ \begin{align} \frac{\partial S_i}{\partial \theta_j} & = \frac{e^{\theta_j} \cdot \sum_{k}e^{\theta_k}- e^{\theta_i} \cdot e^{\theta_j}}{\left( \sum_ke^{\theta_k}\right)^2} \\ \\ & = \frac{e^{\theta_j}}{\sum_ke^{\theta_k}} \cdot \left( 1 - \frac{e^{\theta_j}}{\sum_k e^{\theta_k}} \right) \\ \\ & = S_i \cdot (1 - S_i) \end{align} \] \(i \ne j\)时 \[ \begin{align} \frac{\partial S_i}{\partial \theta_j} & = \frac{ - e^{\theta_i} \cdot e^{\theta_j}}{\left( \sum_ke^{\theta_k}\right)^2} = - S_i \cdot S_j \end{align} \]

交叉熵求梯度

\[ \begin{align} & \rm{CE}(y, \hat y) = - \sum_{i} y_i \times \log (\hat y_i) \\ \\ & \hat y = \rm{S} (\theta)\\ \end{align} \]

只关注有关系的部分，带入\(y_i =1\) ： \[ \begin{align} \frac{\partial CE}{\partial \theta_i} & = -\frac{\partial \log \hat y_i}{\partial \theta_i} = - \frac{1}{\hat y_i} \cdot \frac{\partial \hat y_i}{\partial \theta_i} \\ \\ & = - \frac{1}{S_i} \cdot \frac{\partial S_i}{\partial \theta_i} = S_i - 1 \\ \\ & = \hat y_i - y_i \end{align} \] 不带入求导 \[ \begin{align} \frac{\partial CE}{\partial \theta_i} & = - \sum_{k}y_k \times \frac{\partial \log S_k}{\partial \theta_i} \\ & = - \sum_{k}y_k \times \frac{1}{S_k}\times \frac{\partial S_k}{\partial \theta_i} \\ & = - y_i (1 - S_i) - \sum_{k \ne i} y_k \cdot \frac{1}{S_k} \cdot (- S_i \cdot S_k) \\ & = - y_i (1 - S_i) + \sum_{k \ne i} y_k \cdot S_i \\ & = S_i - y_i \end{align} \] 所以，交叉熵的导数是 \[ \frac{\partial CE}{\partial \theta_i} = \hat y_i - y_i, \quad \quad \frac{\partial CE(y, \hat y)}{\partial \theta} = \hat y - y \]

即 \[ \frac{\partial CE(y, \hat y)}{\partial \theta_i} = \begin{cases} & \hat y_i - 1, & \text{i是label} \\ &\hat y_i, & \text{其它}\\ \end{cases} \]

简单网络

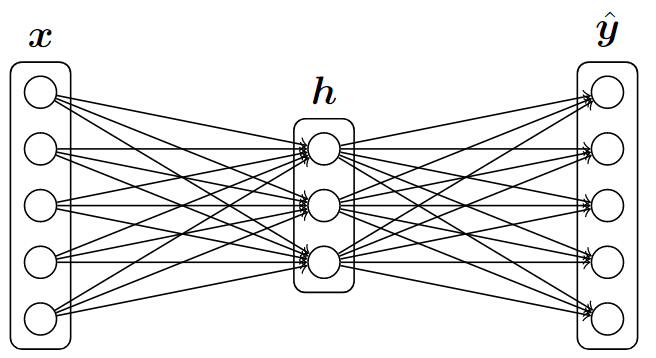
前向计算 \[ \begin{align} & z_1 = xW_1 + b_1 \\ \\ & h = \rm{sigmoid}(z1) \\ \\ & z_2 = hW_2 + b_2 \\ \\ & \hat y = \rm{softmax}(z_2) \end{align} \] 关键代码：

1
2
3
def forward_backward_prop(data, labels, params, dimensions):
    h = sigmoid(np.dot(data, W1) + b1)
    yhat = softmax(np.dot(h, W2) + b2)

loss函数 \[ J = \rm{CE}(y, \hat y) \] 关键代码：

1
2
3
def forward_backward_prop(data, labels, params, dimensions):
    # yhat[labels==1]实际上是boolean索引，见我的numpy_api.ipynb
    cost = np.sum(-np.log(yhat[labels == 1])) / data.shape[0]

反向传播 \[ \begin {align} & \delta_2 = \frac{\partial J}{\partial z_2} = \hat y - y \\ \\ & \frac{\partial J}{\partial h} = \delta_2 \cdot \frac{\partial z_2}{\partial h} = \delta_2 W_2^T \\ \\ & \delta_1 = \frac{\partial J}{\partial z_1} = \frac{\partial J}{\partial h} \cdot \frac{\partial h}{\partial z_1} = \delta_2 W_2^T \circ \sigma^{\prime}(z_1) \\ \\ & \frac{\partial J}{\partial x} = \delta_1 W_1^T \end{align} \] 一共有\((d_x + 1) \cdot d_h + (d_h +1) \cdot d_y\) 个参数。

关键代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def forward_backward_prop(data, labels, params, dimensions):
    # 前面推导的softmax梯度公式
    gradyhat = (yhat - labels) / data.shape[0]
    # 链式法则
    gradW2 = np.dot(h.T, gradyhat)
    # 本地导数是1，把第1维的所有加起来
    gradb2 = np.sum(gradyhat, axis=0, keepdims=True)
    gradh = np.dot(gradyhat, W2.T)
    gradz1 = gradh * sigmoid_grad(h)
    gradW1 = np.dot(data.T, gradz1)
    gradb1 = np.sum(gradz1, axis=0, keepdims=True)
    
    grad = np.concatenate((gradW1.flatten(), gradb1.flatten(),
            gradW2.flatten(), gradb2.flatten()))
    return cost, grad

梯度检查

我的梯度检查

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def gradcheck_naive(f, x):
    fx, grad = f(x) # Evaluate function value at original point
    h = 1e-4        # Do not change this!
    # Iterate over all indexes in x
    it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
    while not it.finished:
        ix = it.multi_index
        # 关键代码
        x[ix] += h
        random.setstate(rndstate)
        new_f1 = f(x)[0]
        x[ix] -= 2 * h
        random.setstate(rndstate)
        new_f2 = f(x)[0]
        x[ix] += h
        numgrad = (new_f1 - new_f2) / (2 * h)

        # Compare gradients
        reldiff = abs(numgrad - grad[ix]) / max(1, abs(numgrad), abs(grad[ix]))
        if reldiff > 1e-5:
            print ("Gradient check failed.")
            print ("First gradient error found at index %s" % str(ix))
            print ("Your gradient: %f \t Numerical gradient: %f" % (
                grad[ix], numgrad))
            return

        it.iternext() # Step to next dimension

Word2Vec

我的word2vec笔记

词向量的梯度

符号定义

  • \(v_c\) 中心词向量，输入词向量，\(V\)， \(\mathbb{R}^{W\times d}\)
  • \(u_o\) 上下文词向量，输出词向量，\(U=[u_1, u_2, \cdots, u_w]\) , \(\mathbb{R}^{d\times W}\)

前向

预测o是c的上下文概率，o为正确单词 \[ \hat y_o = p(o \mid c) = \rm{softmax}(o) = \frac{\exp(u_o^T v_c)}{\sum_{w} \exp(u_w^T v_c)} \] 得分向量： \[ z=U^T \cdot v_c, \quad [W,d] \times[ d] \in ,\mathbb{R}^{W } \] loss及梯度 \[ J_{\rm{softmax-CE}}(v_c, o, U) = CE(y, \hat y), \quad \text{其中} \; \frac{\partial CE(y, \hat y)}{\partial \theta} = \hat y - y \]

梯度 中文 计算 维数
\(\frac{\partial J}{\partial z}\) softmax \(\hat y - y\) \(W\)
\(\frac{\partial J}{\partial v_c}\) 中心词 \(\frac{\partial J}{\partial z} \cdot \frac{\partial z}{\partial v_c} = (\hat y - y) \cdot U^T\) \(d\)
\(\frac{\partial J}{\partial U}\) 上下文 \(\frac{\partial J}{\partial z} \cdot \frac{\partial z}{\partial U^T}= (\hat y - y) \cdot v_c\) \(d \times W\)

关键代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def softmaxCostAndGradient(predicted, target, outputVectors, dataset):
    """ Softmax cost function for word2vec models
    Args:
        predicted: 中心词vc
        target: 上下文uo, index
        outputVectors: 输出，上下文矩阵U，W*d，未转置
        dataset: 
    Returns:
        cost: 交叉熵loss
        gradv: 一维向量
        gradU: W*d
    """
    vhat = predicted
    z = np.dot(outputVectors,vhat)
    preds = softmax(z)
    #  Calculate the cost:
    cost = -np.log(preds[target])
    #  Gradients
    gradz = preds.copy()
    gradz[target] -= 1.0
    gradU = np.outer(z, vhat)
    gradv = np.dot(outputVectors.T, z)
    ### END YOUR CODE
    return cost, gradv, gradU