cs224n神经网络基础,前向反向传播,激活函数等
神经网络基础
很多数据都是非线性分割的,所以需要一种非线性non-linear决策边界 来分类。神经网络包含很多这样的非线性的决策函数。
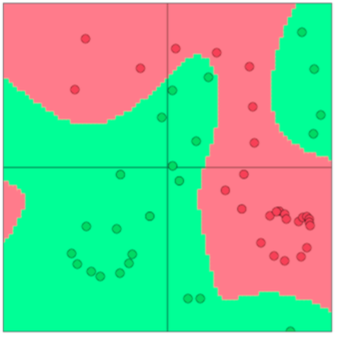
神经元
神经元其实就是一个计算单元。
- 输入向量 \(x \in \mathbb R^n\)
- \(z = w^T x + b\)
- \(a = f(z)\) 激活函数,
sigmoid,relu等,后文有讲。
Sigmoid神经元
传统用sigmoid多,但是现在一定不要使用啦。大多使用Relu作为激活函数。
\[
z = \mathbf{w}^T \mathbf{x} + b , \; a = \frac {1}{1 + \exp (-z)}
\] 
网络层
一个网络层有很多个神经元。输入\(\mathbf x\)向量,会传递到多个神经元。如
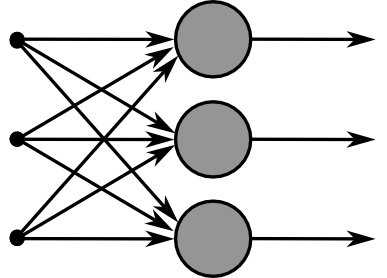
输入是\(n\)维,隐层是\(m\)维,有\(m\)个神经元。则有 \[ \begin{align} & z = W x + b , & W \in \mathbb{R}^{m \times n}, x \in \mathbb R^n, b \in \mathbb R^m\\ & a = f (z) & a \in \mathbb R^m\\ & s = U^T a & 一般会对a进行变换得到最终结果s\\ \end{align} \] 激活函数的意义
每个神经元
- 输入\(z = w^Tx+b\) :对特征进行加权组合的结果
- 激活\(a = f(z)\): 对\(z\)是否继续保留
最后会把所有的神经元的所有\(z\)的激活信息\(a\)综合起来,得到最终的分类结果。比如\(s = U^T a\)。
前向计算
输入\(x \in \mathbb R^n\), 激活信息\(a \in \mathbb R^m\)。一般前向计算如下: \[
\begin{align}
& z = W x + b , & W \in \mathbb{R}^{m \times n}, x \in \mathbb R^n, b \in \mathbb R^m\\\\
& a = f (z) & a \in \mathbb R^m\\\\
& s = U^T a & 一般会对a进行变换得到最终结果s\\
\end{align}
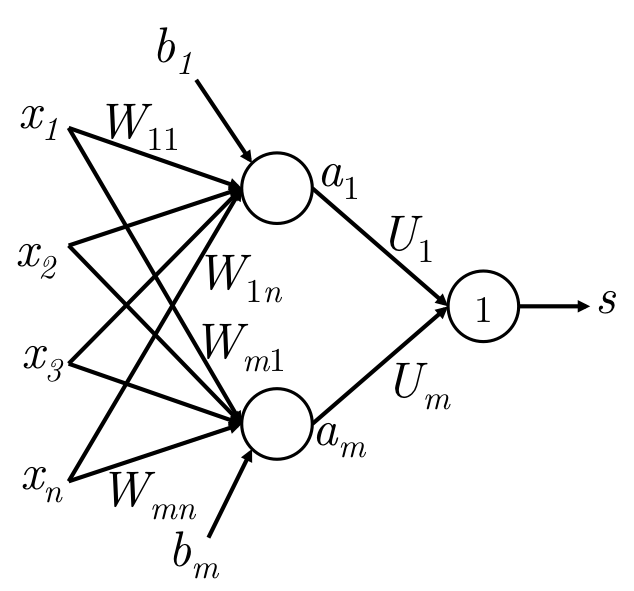
\] 下面是一个简单的全连接,最后的圆圈里的1代表等价输出。
NER例子
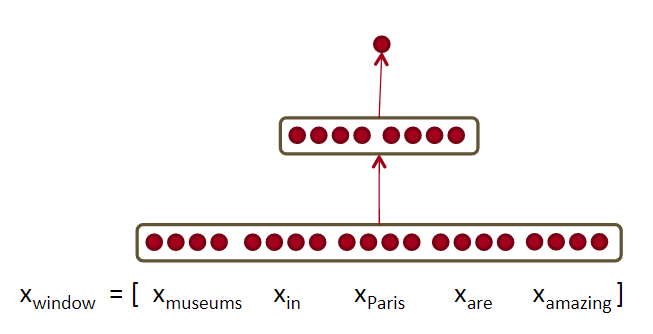
NER(named-entity recognition),命名实体识别。对于一个句子Museums in Paris are amazing。 要判断中心单词Paris是否是个命名实体。
既要看window里的所有词向量,也要看这些词的交互关系。比如:Paris出现在in的后面。 因为可能有Paris和Paris Hilton。这就需要non-linear decisions。
如果直接把input给到softmax,是很难获取到非线性决策的。所以需要添加中间层使用神经网络。如上图所示。
维数分析
每个单词4维,输入整个窗口就是20维。在隐层使用8个神经元。计算过程如下,最终得到一个分类的得分。 \[
\begin {align}
& z = Wx + b \\
& a = f(z) \\
& s = U^T a \\
\end{align}
\] 维数如下: \[
x \in \mathbb R^{20}, \; W \in \mathbb R^{8\times20}, \; U \in \mathbb R^{8\times1}, s \in R
\] 
Max magin目标函数
正样本\(s\) :Museums in Paris are amazing ,负样本\(s_c\): Not all museums in Paris 。
只关心:正样本的得分高于负样本的得分, 其它的不关注。即要\(s - s_c > 0\): \[
\mathrm{maxmize}(s -s_c) \leftrightarrow \mathrm{minmize}(s_c - s)
\] 优化目标函数如下: \[
\rm{minimize} \; J =
\max(s_c - s, 0) \;
= \begin{cases}
& s_c - s, & s < s_c \\
& 0, & s \ge s_c
\end{cases}
\] 上式其实有风险,更需要\(s - s_c > \Delta\), 即\(s\)比\(s_c\)得分大于\(\Delta\),来保证一个安全的间距。 \[
\rm{minimize} \; J = \max(\Delta + s_c - s, 0)
\] 给具体间距\(\Delta=1\), 所以优化目标函数:详情见SVM。 \[
\rm{minimize} \; J = \max(1 + s_c - s, 0)
\] 其中\(s_c = U^T f(Wx_c + b), \; s = U^T f(Wx+b)\) 。
反向传播训练
梯度下降 ,或者SGD: \[
\theta^{(t+1)} = \theta^{(t)} - \alpha \cdot \Delta_{\theta^{(t)}} J
\] 反向传播 使用链式法则 来计算前向计算中用到的参数的梯度。
符号定义
如下图,一个简单的网络:
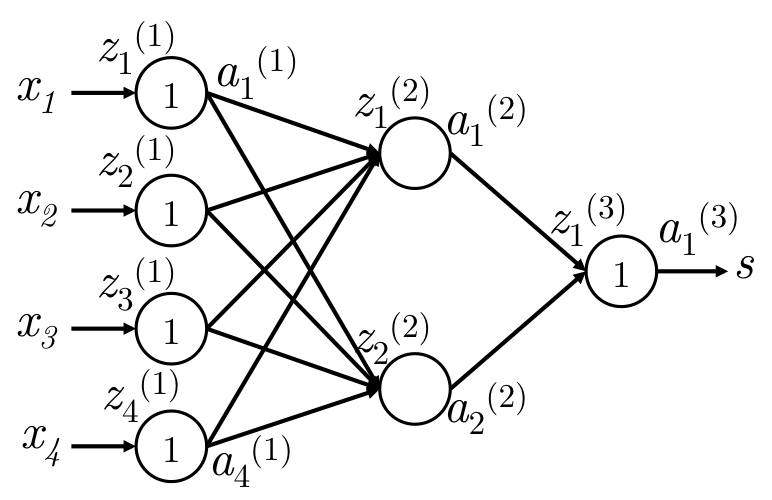
网络在输入层和输出层是等价输入和等价输出,只有中间层会使用激活函数进行非线性变换。
| 符号 | 意义 |
|---|---|
| \(x\) | 网络输入,这里是4维 |
| \(s\) | 网络输出,这里是1维,即一个数字 |
| \(W^{(k)}\) | 第\(k \to k+1\)层的转移矩阵。\(W \in \mathbb R^{n \times m}\)。 k层m个神经元,k+1层n个神经元 |
| \(W_{ij}^{(k)}\) | k+1层的\(i\) 神经元 到 到\(k\)层\(j\)神经元的 的权值 |
| \(b_i^{(k)}\) | \(k \to k+1\) 转移, k+1层的\(i\) 神经元的接收偏置 |
| \(z^{(k)}_j\) | 第\(k\)层的第\(j\)个神经元的输入 |
| 计算输入 | \(z_j^{(k+1)} = \sum_i W_{ji}^{(k)} \cdot a^{(k)}_i + b^{(k)}_j\) |
| \(a_j^{(k)}\) | 第\(k\)层的第\(j\)个神经元的输入。\(a = f(z)\) |
| \(\delta_j^{(k)}\) | BP时,在\(z_j^{(k)}\)处的梯度。即\(f^\prime(z_j^{(k)}) \cdot g\) ,\(g\)是传递来的梯度 |
W梯度推导
误差函数\(J = \max (1 + s_c - s, 0)\) ,当\(J > 0\)的时候,\(J = 1 + s_c - s\)要去更新参数W和b。 \[
\frac{\partial J} {\partial s} = - \frac{\partial J} {\partial s_c} = -1
\] 反向传播时,必须知道参数在前向时所贡献所关联的对象,即知道路径。

这里是等价输出: \[ s = a_1^{(3)} = z_1^{(3)} = W_1^{(2)}a_1^{(2) } + W_2^{(2)}a_2^{(2) } \] 这里对\(W_{ij}^{(1)}\)的偏导进行反向传播推导: \[ \begin{align} \frac{\partial s}{\partial W_{ij}^{(1)}} & = \frac{\partial W^{(2)} a^{(2)}}{\partial W_{ij}^{(1)}} \\ &= \frac{ \color{blue} {\partial W_i^{(2)} a_i^{(2)}}} {\partial W_{ij}^{(1)}} = \color{blue}{W_i^{(2)}} \cdot \frac{\partial a_i^{(2)}}{\partial W_{ij}^{(1)}} \\ & = W_i^{(2)} \cdot \color{blue} {\frac{\partial a_i^{(2)}}{\partial z_i^{(2)}} \cdot \frac{\partial z_i^{(2)}}{\partial W_{ij}^{(1)}}} \\ & = W_i^{(2)} \cdot \color{blue}{f^\prime(z_i^{(2)})} \cdot \frac{\partial }{\partial W_{ij}^{(1)}} \left(\color{blue}{b_i^{(2)} + \sum_k^4 a_k^{(1)}W_{ik}^{(1)}}\right) \\ & = W_i^{(2)}f^\prime(z_i^{(2)}) \color{blue}{a_j^{(1)}} \\ & = \color{blue}{\delta^{(2)}_i} \cdot a_j^{(1)} \end{align} \] 结果分析
我们知道\(z_i^{(2)} = \sum_k^4 a_k^{(1)}W_{ik}^{(1)} + b_i^{(2)}\)。 单纯\(z_i^{(2)}\)对\(W_{ij}^{(2)}\)的导数是\(a_j^{(1)}\)。反向时,在\(z_i^{(2)}\)处的梯度是\(\delta_i^{(2)}\)。
反向时,\(\frac{\partial s}{\partial W_{ij}^{(1)}} = \delta^{(2)}_i \cdot a_j^{(1)}\),是传来的梯度和当前梯度的乘积。这正好应证了反向传播。 传来的梯度也作error signal。 反向过程也是error sharing/distribution。
W元素实例
\(W_{14}^{(1)}\) 只直接贡献于\(z_1^{(2)}\)和\(a_1^{(2)}\)
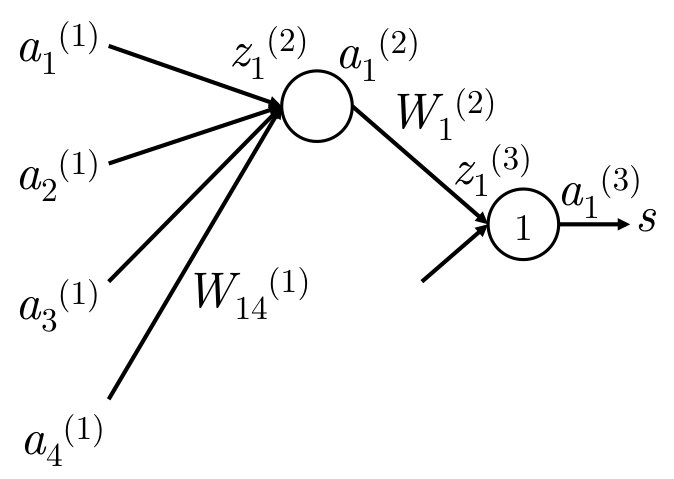
| 步骤 | 梯度 |
|---|---|
| \(s \to a_1^{(3)}\) | 梯度\(g=1\)。开始为1。 |
| \(a_1^{(3)} \to z_1^{(3)}\) | 在\(z_1^{(3)}\)处的梯度\(g = 1 \cdot 1 = \delta_1^{(3)}\) 。\(local \; g= 1\) ,等价变换 |
| \(z_1^{(3)} \to a_1^{(2)}\) | \(g = \delta_1^{(3)} \cdot W_1^{(2)} = W_1^{(2)}\) 。\(lg = w\), \(z=wa+b\) |
| \(a_1^{(2)} \to z_1^{(2)}\) | \(g = W_1^{(2)} \cdot f^\prime(z_1^{(2)}) = \delta_1^{(2)}\)。 \(lg=f^\prime(z_1^{(2)})\) |
| \(z_1^{(2)} \to W_{14}^{(1)}\) | \(g =W_1^{(2)} \cdot f^\prime(z_1^{(2)}) \cdot a_4^{(1)} = \delta_1^{(2)} \cdot a_4^{(1)}\)。 \(lg = a_4^{(1)}\) , 因为\(z =wa+b\) |
| \(z_1^{(2)} \to b_1^{(1)}\) | \(g = W_1^{(2)} \cdot f^\prime(z_1^{(2)}) \cdot 1 = \delta_1^{(2)} \cdot a_4^{(1)}\)。 \(lg = 1\) , 因为\(z =wa+b\) |
对于上式的梯度计算,有两种理解方法,通过这两种思路去思考能更深入了解。
链式法则error sharing and distributed flow approach
梯度反向传播
\(\delta_i^{(k)} \to \delta_j^{(k-1)}\) 传播图如下:
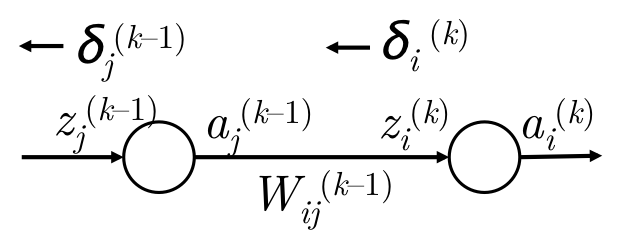
但是更多时候,当前层的某个神经元的信息会传播到下一层的多个节点上,如下图:
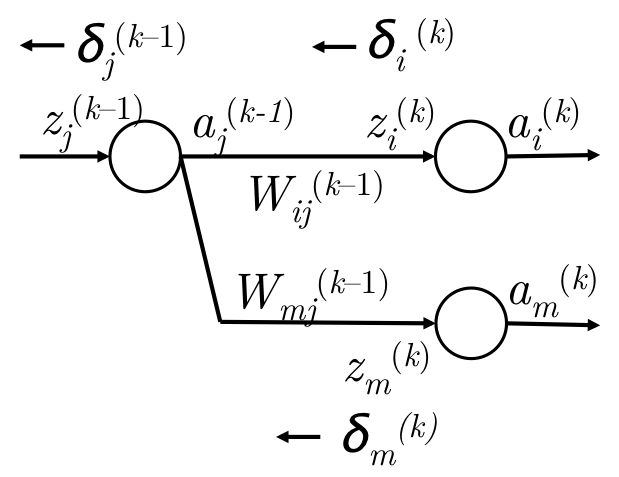
梯度推导公式如下: \[ \begin{align} & g_w = \delta_i^{(k)} \cdot a_j^{(k-1)} & W_{ij}^{(k-1)}的梯度\\\\ & g_a = \sum_i \delta_i^{(k)}W_{ij}^{(k-1)} & a_j^{(k-1)}的梯度 \\\\ & g_z = \delta_j^{(k-1)} = f^\prime(z_j^{(k-1)}) \cdot \sum_i \delta_i^{(k)}W_{ij}^{(k-1)} & z_j^{(k-1)}的梯度 \\\\ \end{align} \]
BP向量化
很明显,不能一个一个参数地去更新element-wise。所以需要用矩阵和向量去表达,去一次性全部更新matrix-vector level。
梯度计算, \(W_{ij}^{(k)}\)的梯度是\(\delta_i^{(k+1)} \cdot a_j^{(k)}\) 。向量表达如下: \[
\Delta _{W^{(k)}} =
\begin{bmatrix}
\delta_1^{(k+1)} \cdot a_1^{(k)} & \delta_1^{(k+1)} \cdot a_2^{(k)} & \cdots\\
\delta_2^{(k+1)} \cdot a_1^{(k)} & \delta_2^{(k+1)} \cdot a_2^{(k)} & \cdots \\
\vdots & \vdots & \ddots
\end{bmatrix}
= \delta^{(k+1)} a^{(k)T}
\] 梯度传播,\(\delta_j^{(k)} = f^\prime(z_j^{(k)}) \cdot \sum_i \delta_i^{(k+1)}W_{ij}^{(k)}\)。向量表达如下: \[
\delta^{(k)} = f^\prime(z^{(k)}) \circ (\delta^{(k+1)}W^{(k)})
\] 其中\(\circ\)是叉积向量积element-wise,是各个位置相乘, 即\(\mathbb R^N \times \mathbb R^N \to \mathbb R^N\)。 点积和数量积是各个位置相乘求和。
计算效率
很明显,在计算的时候要把上一层的\(\delta^{(k+1)}\)存起来,去计算\(\delta^{(k)}\) ,这样可以减少大量的多余的计算。
神经网络常识
梯度检查
使用导数的定义来估计导数,去和BP算出来的梯度做对比。
\[
f ^\prime (\theta) \approx \frac{J(\theta^{(i+)}) - J(\theta^{(i-)})} {2 \epsilon }
\] 由于这样计算非常,效率特别低,所以只用这种办法来检查梯度。具体实现代码见原notes。
激活函数
激活函数有很多,现在主要用ReLu,不要用sigmoid。
用ReLU学习率一定不要设置太大!同一个网络中都使用同一种类型的激活函数。
Sigmoid
数学形式和导数如下: \[ \begin{align} & \sigma (z) = \frac {1} {1 + \exp(-z)}, \; \sigma(z) \in (0,1) \\ \\ & \sigma^\prime (z) = \sigma(z) (1 - \sigma(z)) \\ \end{align} \] 图像
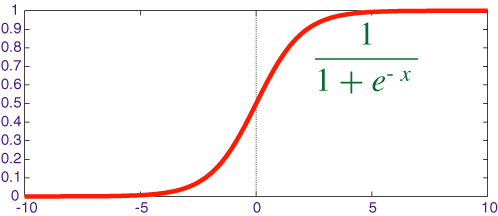
优点是具有好的解释性,将实数挤压到\((0,1)\)中,很大的负数变成0,很大的正数变成1 。但现在用的已经越来越少了。有下面2个缺点。
Sigmoid会造成梯度消失
- 靠近0和1两端时,梯度会变成0。 BP链式法则,\(0 \times g_{from} = 0\) ,后面的梯度接近0, 将没有信息去更新参数。
- 初始化权重过大,大部分神经元会饱和,无法更新参数。因为输入值很大,靠近1了。\(f^\prime(z) = 0\), 没法传播了。
Sigmoid输出不是以0为均值
- 如果输出\(x\)全是正的,\(z=wx+b\), 那么\(\frac{\partial z}{\partial w} = x\) 梯度就全是正的
- 不过一般是batch训练,其实问题也还好
Sigmoid梯度消失的问题最严重。
Tanh
数学公式和导数如下: \[ \begin{align} & \tanh (z) = \frac{\exp(z) - \exp(-z)}{\exp(z) + \exp(-z)} = 2 \sigma(2z) - 1, \; \tanh(z) \in(-1, 1) \\ \\ & \tanh^\prime (z) = 1 - \tanh^2 (z) \end{align} \] 图像:
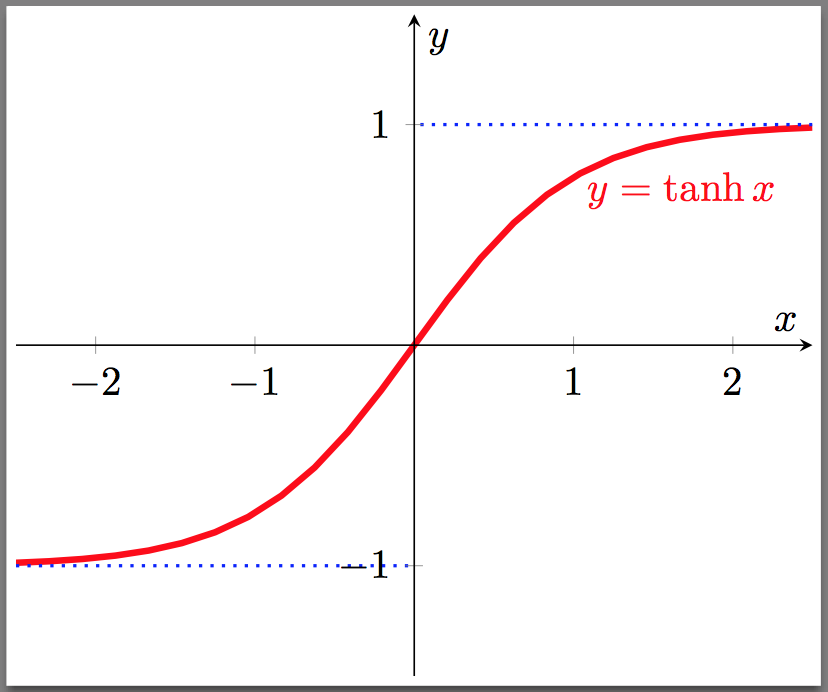
Tanh是Sigmoid的代替,它是0均值的,但是依然存在梯度消失的问题。
ReLU
ReLURectified Linear Unit 最近越来越流行,不会对于大值\(z\)就导致神经元饱和的问题。在CV取得了很大的成功。 \[
\begin{align}
& \rm{rect}(z) = \max(z, 0) \\ \\
& \rm{rect}^\prime (z) =
\begin{cases} &1, &z > 0 \\& 0, & z \le 0 \end{cases}
\\
\end{align}
\] 其实ReLU是一个关于0的阈值,现在一般都用ReLU:
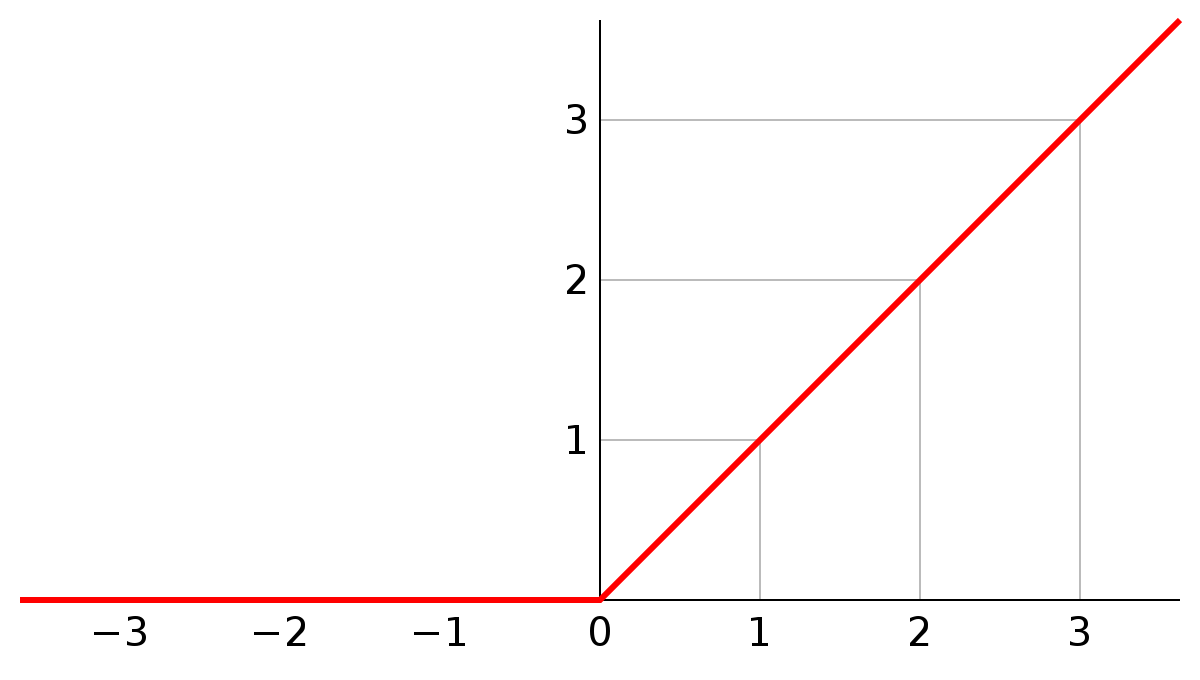
ReLU的优点
- 加速收敛(6倍)。线性的,不存在梯度消失的问题。一直是1。
- 计算简单
ReLU的缺点
训练的时候很脆弱
- BP时,如果有大梯度经过ReLU,当前在z处的梯度\(\delta^{(k+1)} = 1 \times g_m\) 就很大
- 对参数\(w\)的梯度 \(\Delta_{W^{(k)}} =\delta^{(k)} a^{(k)T}\) 也就很大
- 参数\(w\)会更新的特别小 \(W^{(k)} = W^{(k)} - \alpha \cdot \Delta_{W^{(k)}}\)
- 前向时,\(z =wx+b \le 0\) 也就特别小,激活函数就不会激活
- 不激活,梯度就为0。
- 再BP的时候,就无法更新参数了
总结也就是:大梯度\(\to\)小参数\(w\) ,新小$z = wx+b $ ReLU不激活, 不激活梯度为0 \(\to\) 不更新参数w了。
当然可以使用比较小的学习率来解决这个问题。
Maxout
maxout 有ReLU的优点,同时避免了它的缺点。但是maxout加倍了模型的参数,导致了模型的存储变大。 \[
\begin{align}
& \rm{mo}(x) = \max(w_1x+b_1, w_2x+b_2) \\ \\
& \rm{mo}^\prime (x) =
\begin{cases} &w_1, &w_1x+b_1 大 \\& w_2, & 其它 \\\end{cases}
\\
\end{align}
\]
