吴恩达线性回归、逻辑回归、梯度下降笔记
线性回归
有\(m\)个样本\((x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), \cdots, (x^{(m)}, y^{(m)})\),假设函数有2个参数\(\theta_0, \theta_1\),形式如下: \[ h_\theta(x) = \theta_0 + \theta_1x \]
代价函数
代价函数 \[ \color{red} {J(\theta_0, \theta_1) = \frac {1}{2m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)}\right)^2} \] 目标是要找到合适的参数,去最小化代价函数\(min\, J(\theta_0, \theta_1)\)。
假设\(\theta_0 = 0\),去描绘出\(J(\theta_1)\)和\(\theta_1\)的关系,如下面右图所示。

假设有3个样本\((1,1), (2,2), (3,3)\),图中选取了3个\(\theta_1 = 1, 0.5, 0\),其中\(J(\theta_1)\)在\(\theta_1=1\)时最小。
那么回到最初的两个参数\(h_\theta(x) = \theta_0 + \theta_1x\),如何去找\(min\, J(\theta_0, \theta_1)\)呢?这里绘制一个等高图去表示代价函数,如下面右图所示,其中中间点是代价最小的。

梯度下降
基础说明
上文已经定义了代价函数\(J(\theta_0, \theta_1)\),这里要使用梯度下降算法去最小化\(J(\theta_0, \theta_1)\),自动寻找出最合适的\(\theta\)。梯度下降算法应用很广泛,很重要。大体步骤如下:
- 设置初始值\(\theta_0, \theta_1\)
- 不停改变\(\theta_0, \theta_1\)去减少\(J(\theta_0, \theta_1)\)
当然选择不同的初始值,可能会得到不同的结果,得到局部最优解。
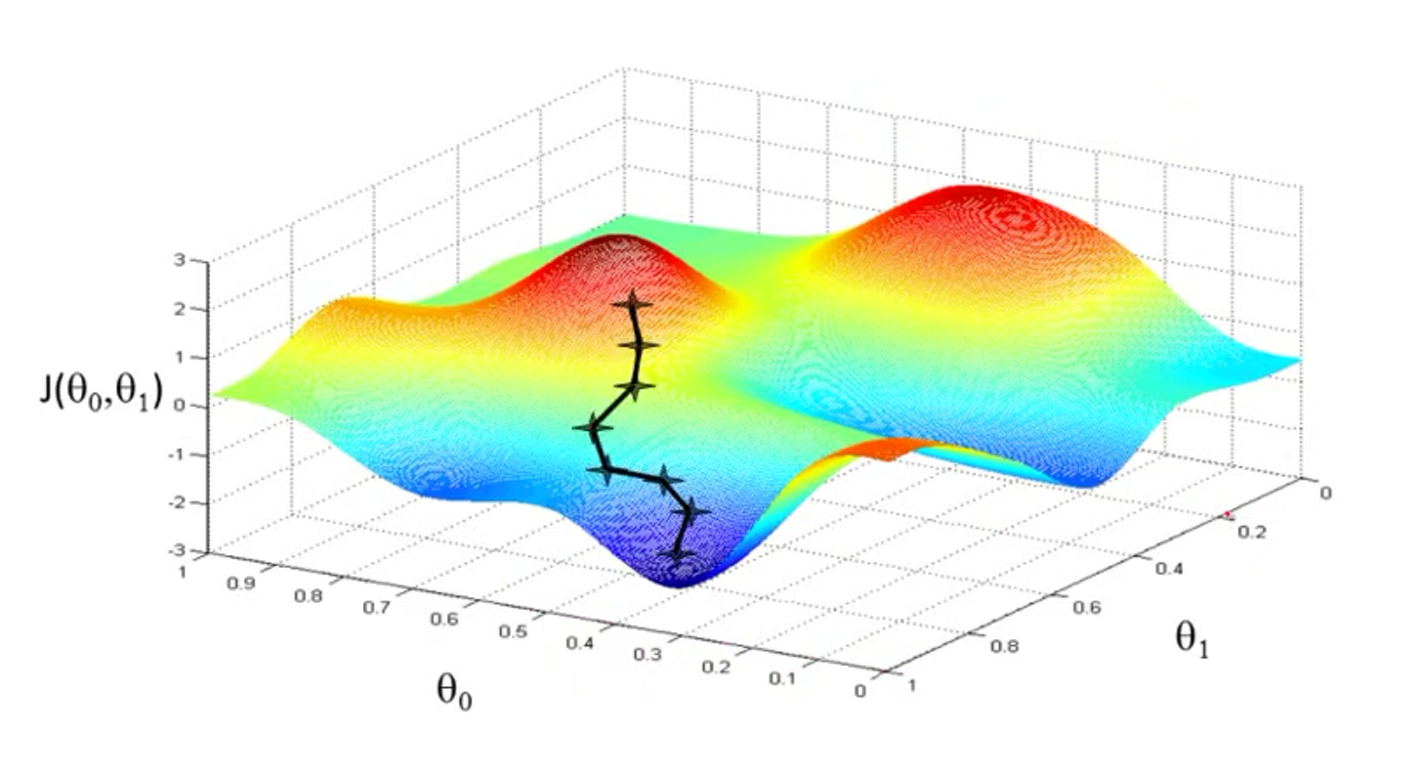
对于所有的参数\(\theta_j\)进行同步更新,式子如下 \[
\color{red}{\theta_j = \theta_j - \underbrace{\alpha \cdot \frac{\partial}{\partial_{\theta_j}} J(\theta_0, \theta_1)}_{学习率 \times 偏导}}
\] 上面公式中\(\color{blue}{\alpha}\)是学习率(learning rate),是指一次迈多大的步子,一次更新的幅度大小。
例如上面的两个参数,对于一次同步更新(梯度下降) \[ t_0 = \theta_0 - \alpha \frac{\partial}{\partial_{\theta_0}} J(\theta_0, \theta_1), t_1 = \theta_1 - \alpha \frac{\partial}{\partial_{\theta_1}} J(\theta_0, \theta_1) \quad \to\quad \theta_0 = t_0, \theta_1 = t_1 \] 也有异步更新(一般指别的算法) \[ t_0 = \theta_0 - \alpha \frac{\partial}{\partial_{\theta_0}} J(\theta_0, \theta_1),\theta_0 = t_0 \quad \to\quad t_1 = \theta_1 - \alpha \frac{\partial}{\partial_{\theta_1}} J(\theta_0, \theta_1), \theta_1 = t_1 \] 偏导和学习率
这里先看一个参数的例子,即\(J(\theta_1)\)。\(\theta_1 = \theta_1 - \alpha \frac{d}{dx}J(\theta_1)\)。当\(\theta\)从左右靠近中间值,导数值(偏导/斜率)分别是负、正,所以从左右两端都会靠近中间值。
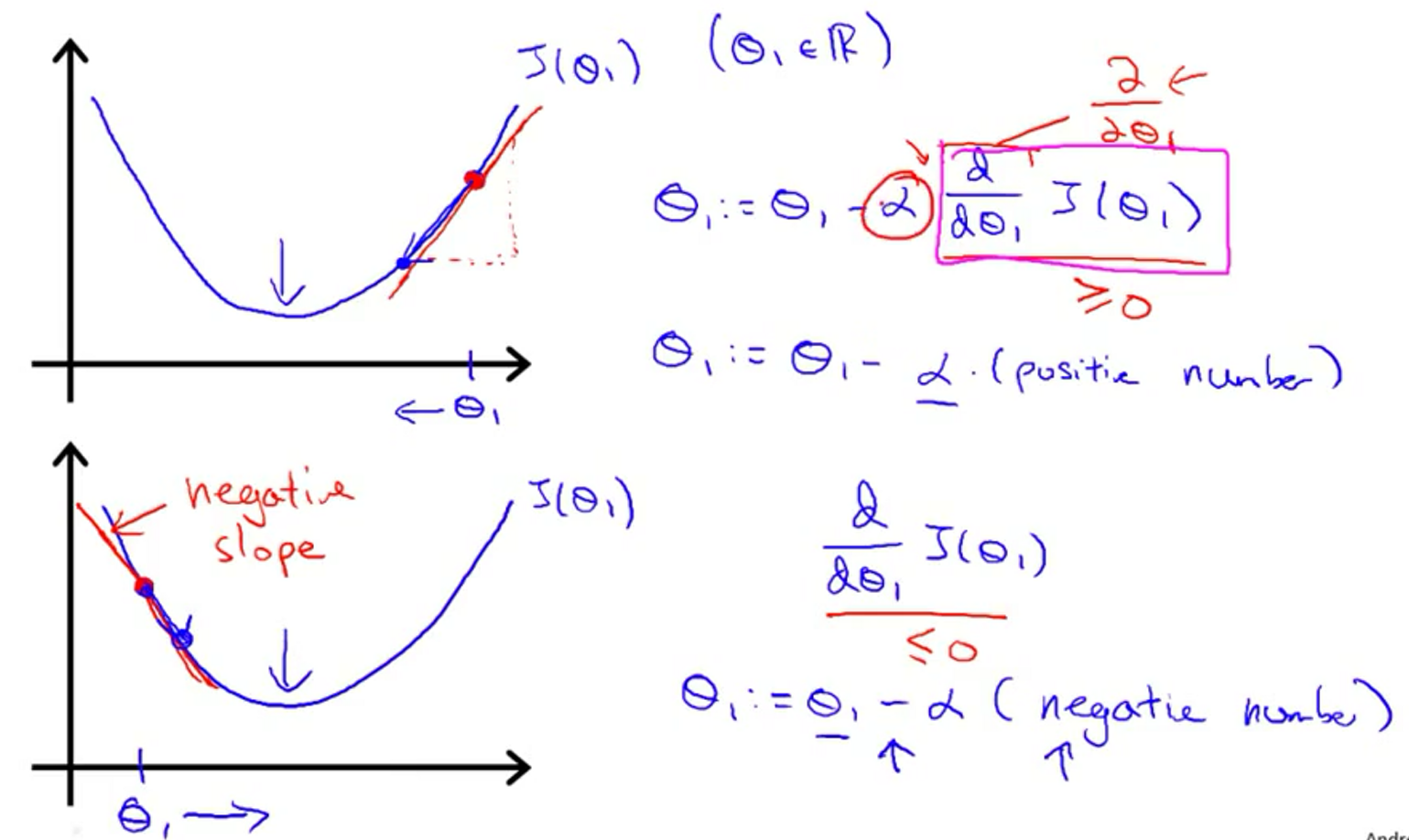
当学习率\(\alpha\)太小,梯度下降会很缓慢;\(\alpha\)太大,可能会错过最低点,导致无法收敛。

当已经处于局部最优的时候,导数为0,并不会改变参数的值,如下图
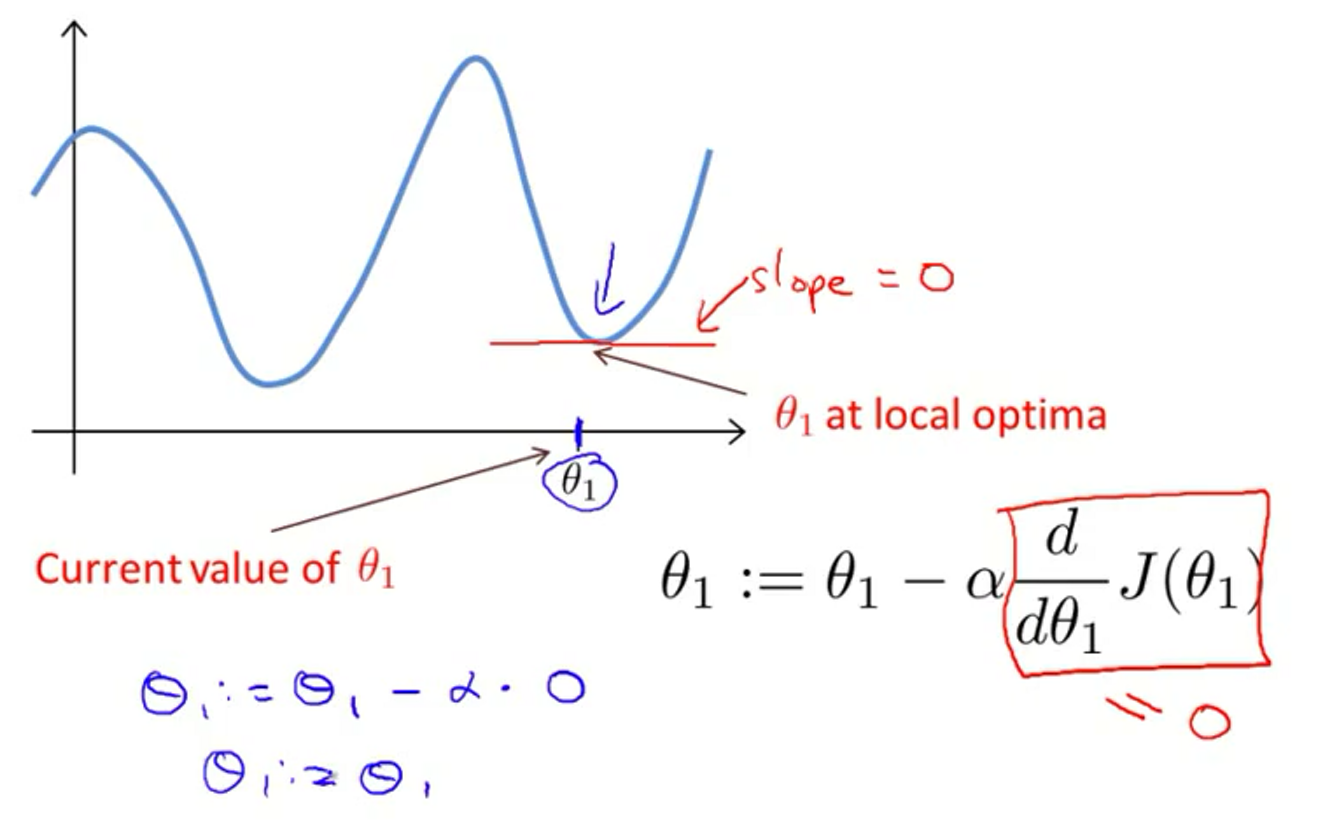
当逐渐靠近局部最优的时候,梯度下降会自动采取小步子到达局部最优点。是因为越接近,导数会越来越小。
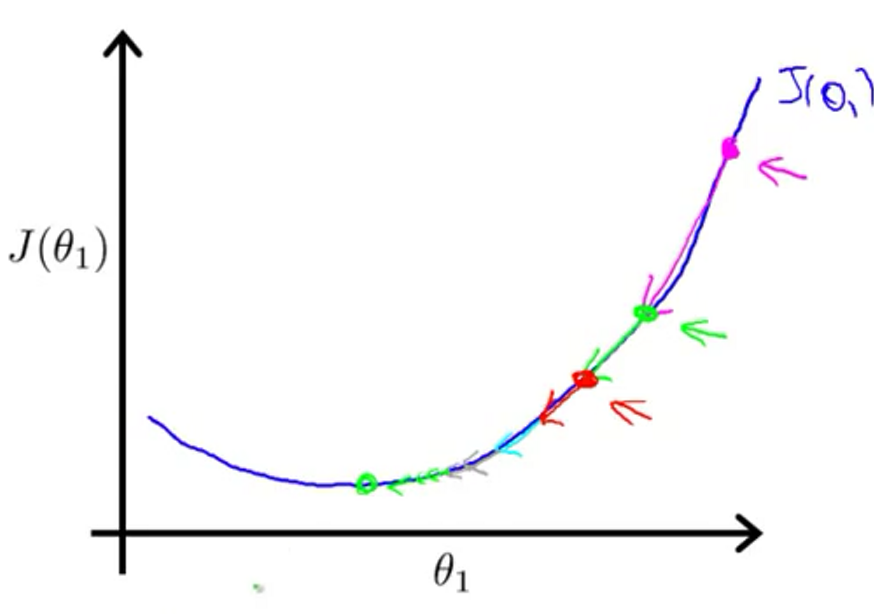
在线性回归上使用梯度下降
代价函数 \[ \color{blue} {J(\theta_0, \theta_1)} = \frac {1}{2m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)}\right)^2 = \color{red}{\frac{1}{2m} \sum_{i=1}^m (\theta_0 + \theta_1x^{(i)} -y^{(i)})^2} \] 分别对\(\theta_0\)和\(\theta_1\)求偏导有 \[ \color{blue}{\frac{\partial}{\partial_{\theta_0}}J(\theta_0, \theta_1) }= \frac{1}{m} \sum_{i=1}^m\left(h_\theta(x^{(i)}) - y^{(i)}\right), \quad \color{blue}{\frac{\partial}{\partial_{\theta_1}} J(\theta_0, \theta_1)}= \frac{1}{m} \sum_{i=1}^m\left(h_\theta(x^{(i)}) - y^{(i)}\right)\cdot x^{(i)} \] 那么使用梯度下降对\(\theta_0 和 \theta_1\)进行更新,如下 \[ \theta_0 = \theta_0 - \alpha \frac{1}{m} \sum_{i=1}^m\left(h_\theta(x^{(i)}) - y^{(i)}\right), \quad \theta_1 = \theta_1 - \alpha \frac{1}{m} \sum_{i=1}^m\left(h_\theta(x^{(i)}) - y^{(i)}\right)\cdot x^{(i)} \] 当前代价函数实际上是一个凸函数,如下图所示。它只有全局最优,没有局部最优。
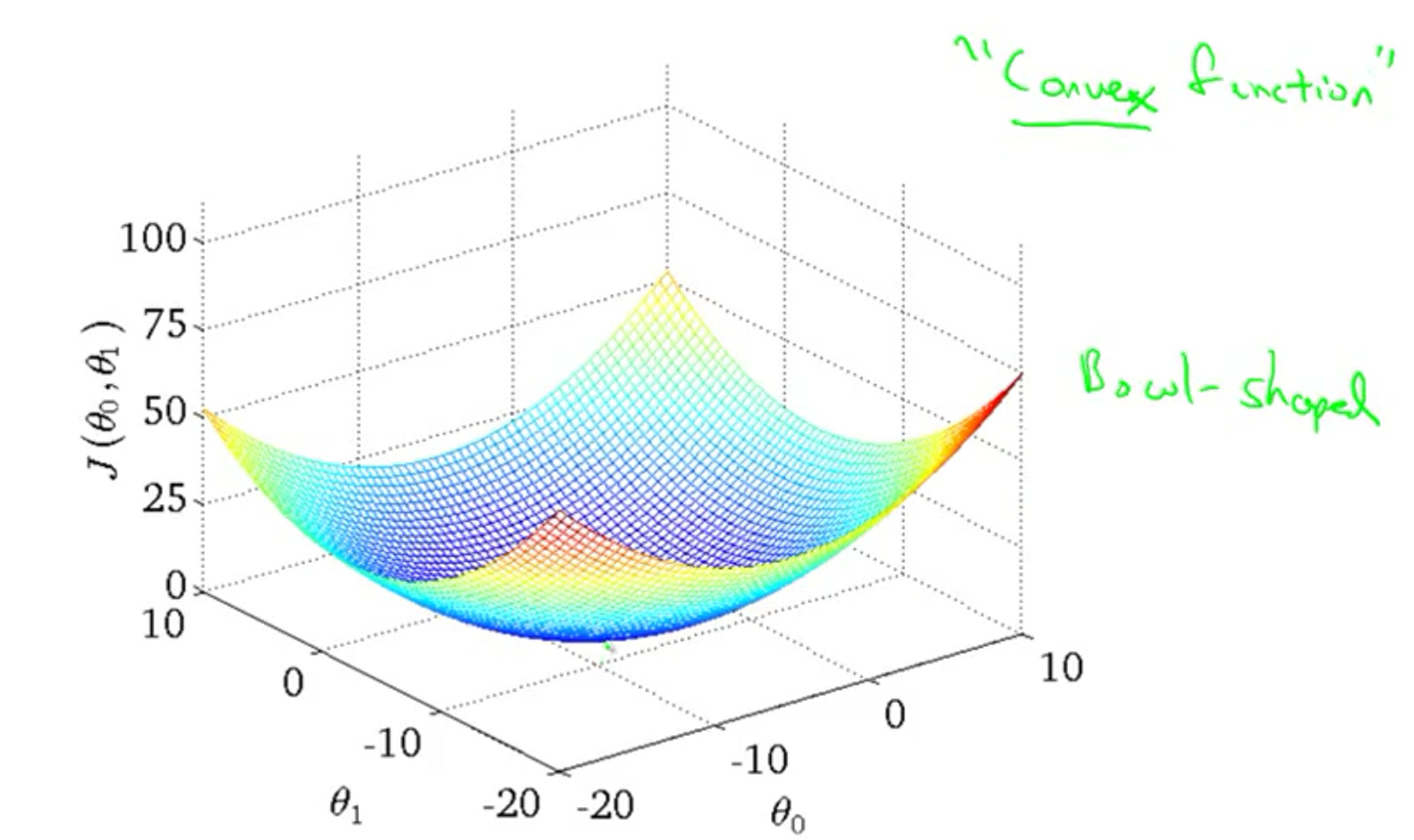
通过不断地改变参数减小代价函数\(\color{blue} {J(\theta_0, \theta_1)}\),逼近最优解,最终会得到一组比较好的参数,正好拟合了我们的训练数据,就可以进行新的值预测。
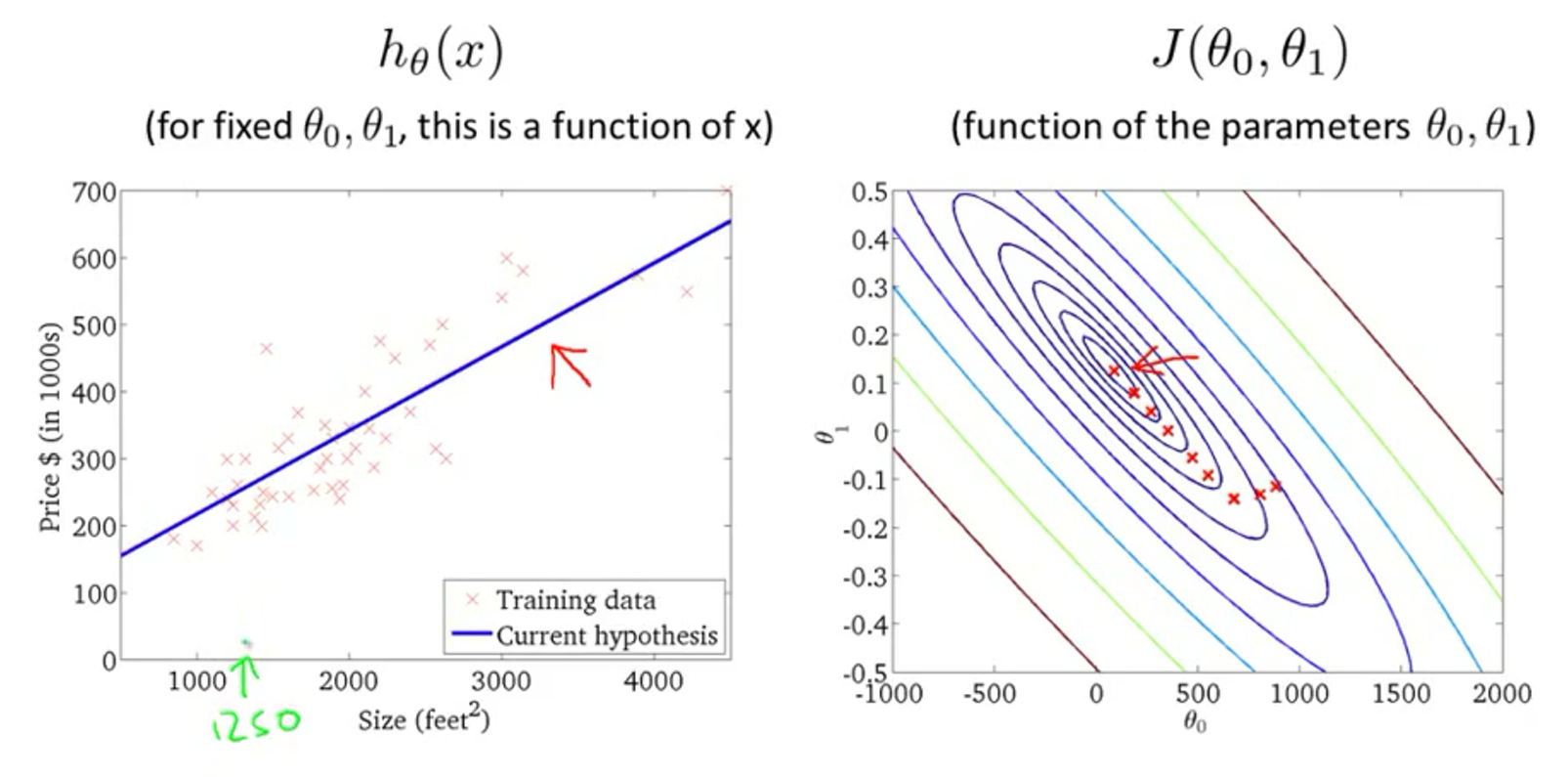
梯度下降技巧
特征缩放
不同的特征的单位的数值变化范围不一样,比如\(x_1 \in (0,2000), x_2 \in (1,5)\),这样会导致代价函数\(J(\theta)\)特别的偏,椭圆。这样来进行梯度下降会特别的慢,会来回震荡。
所以特征缩放是把所有的特征缩放到相同的规模上。得到的\(J(\theta)\)就会比较圆,梯度下降能很快地找到一条通往全局最小的捷径。
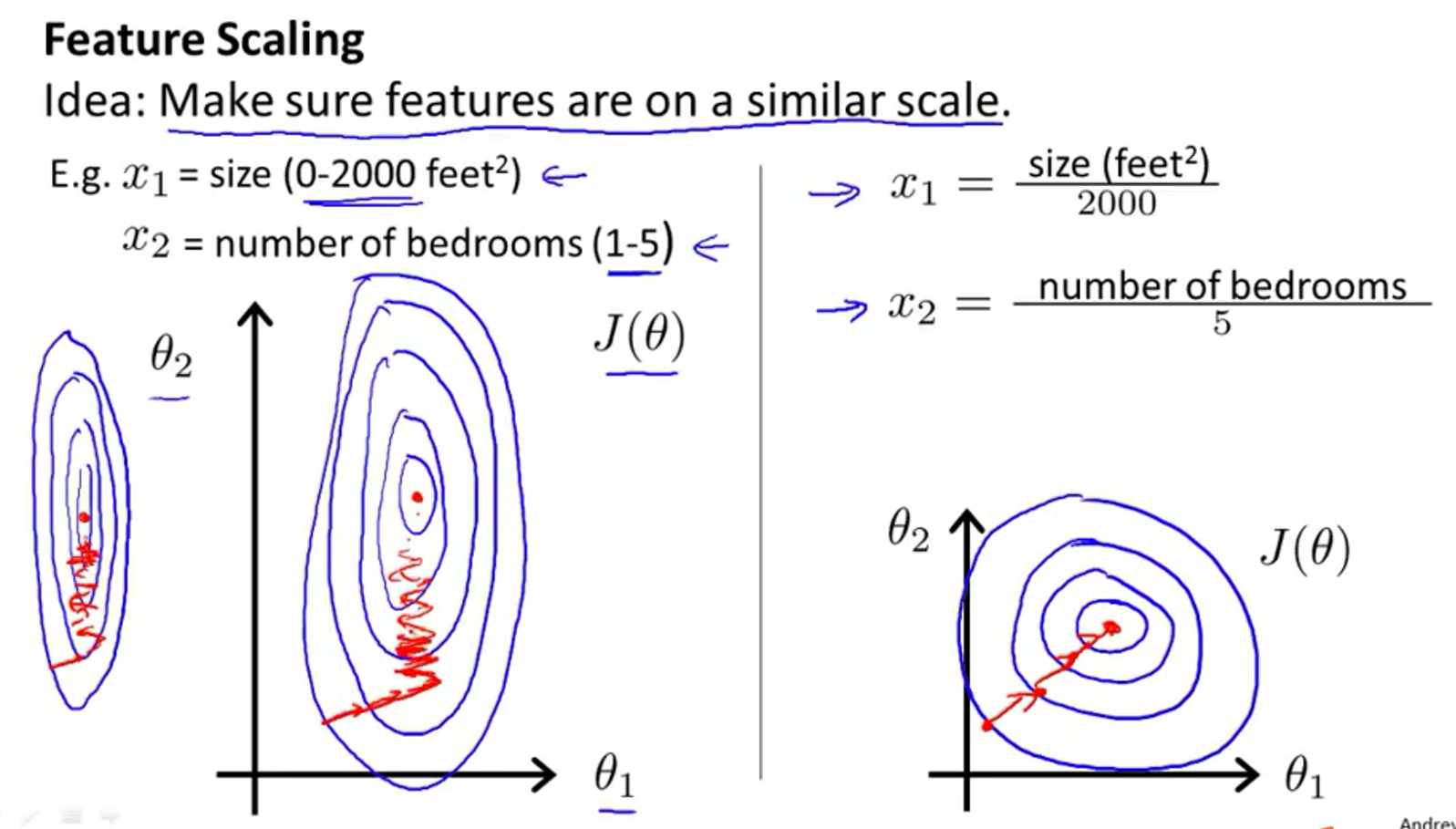
特征缩放的数据规模不能太小或者太大,如下面可以的规模是 \[ [-1, 1], [0, 3], [-2, 0.5], [-3, 3], [-\frac{1}{3}, \frac{1}{3}] 都是可以的。而[-100, 100], [-0.0001, 0.0001]是不可以的 \] 有一些常见的缩放方法
- \(x_i = \frac{x_i - \mu}{max - min}\), \(x_i = \frac{x_i - \mu}{s}\),其中\(\mu\)是均值,\(s\)是标准差
- \(x_i = \frac{x_i - min} {max - min}\)
- \(x_i = \frac{x_i}{max}\)
学习率的选择
当梯度下降正确运行的时候,每一次迭代\(J(\theta)\)都会减少,但是减少到什么时候合适呢?当然最好的办法就是画图去观察,当然也可以设定减小的最小值来判断。下图中, 迭代次数到达400的时候就已经收敛。不同的算法,收敛次数不一样。
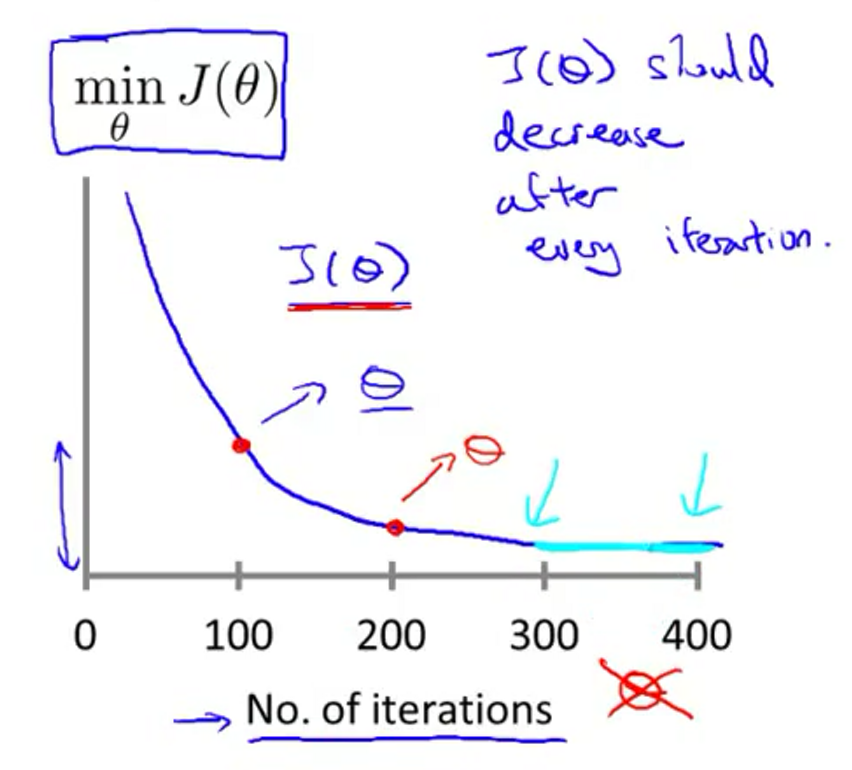
当图像呈现如下的形状,就需要使用更小的学习率。理论上讲,只要使用足够小的学习率,\(J(\theta)\)每次都会减少。但是太小的话,梯度下降会太慢,难以收敛。
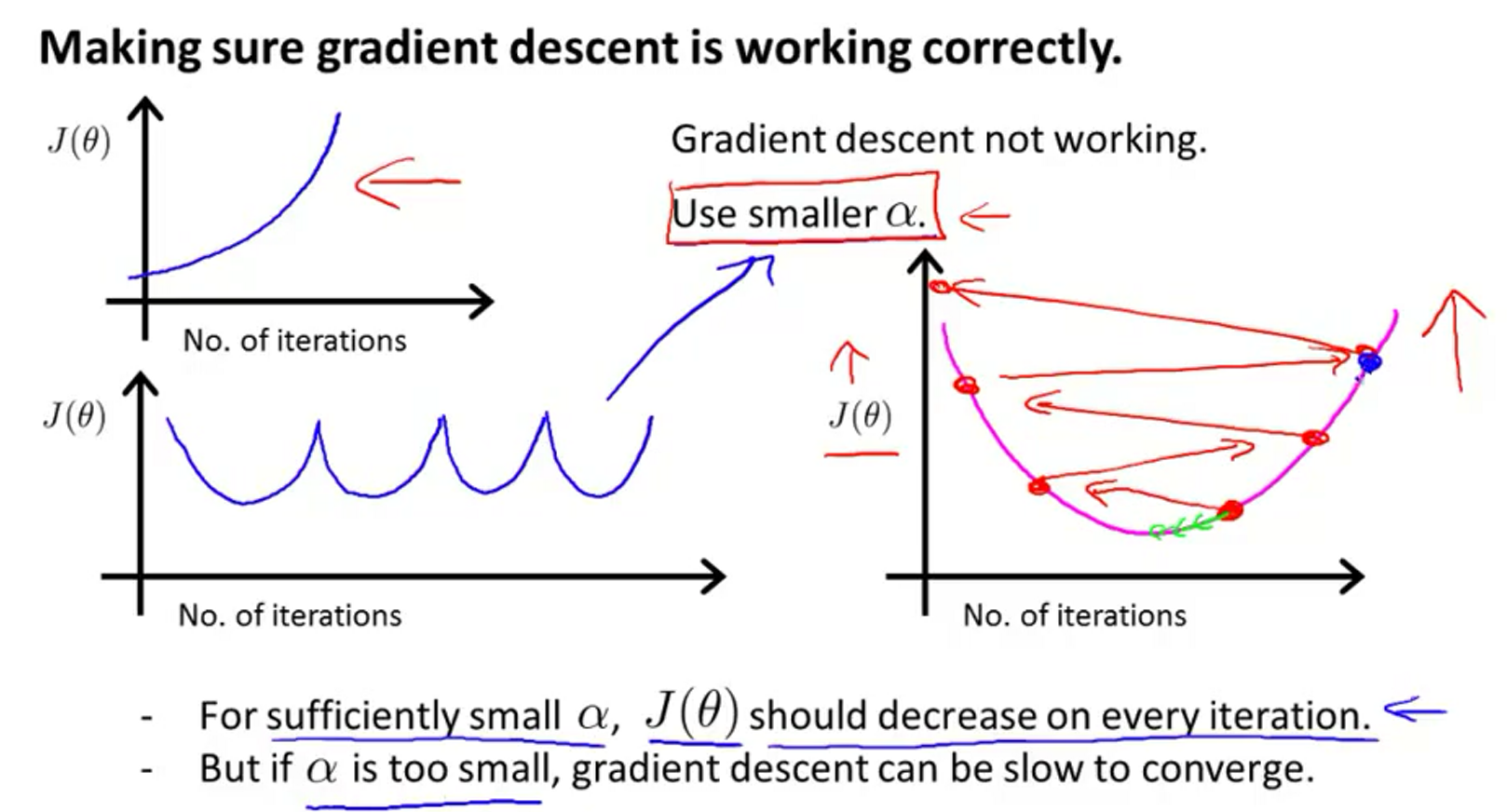
学习率总结
- 学习率太小,慢收敛
- 学习率太大,\(J(\theta)\)可能不会每次迭代都减小,甚至不会收敛
- 这样去选择学习率调试: \(\ldots, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, \ldots\)
多变量线性回归
数据有\(n\)个特征,如\(x^{(i)} = (1, x_1, x_2, \cdots, x_n)\),其中\(x_0 = 1\)。则假设函数有\(n+1\)个参数,形式如下 \[ \color{blue}{h_\theta(x)} = \theta^Tx = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \cdots + \theta_n x_n \] 代价函数 \[ \color{blue}{J(\theta)} = \frac{1}{2m} \sum_{i=1}^m\left( h_\theta(x^{(i)}) - y^{(i)}\right) ^ 2 \] 梯度下降,更新每个参数\(\theta_j\) \[ \theta_j = \theta_j - \alpha \cdot \frac{\partial J(\theta)}{\partial_{\theta_j}} =\color{red}{ \theta_j -\alpha \cdot \frac{1}{m} \sum_{i=1}^m \left(h_\theta(x^{(i)})-y^{(i)} \right) \cdot x_j^{(i)}} \]
多项式回归
有时候,线性回归并不能很好地拟合数据,所以我们需要曲线来适应我们的数据。比如一个二次方模型 \[ h_\theta(x) = \theta_0 + \theta_1x_1 + \theta_2x^2_2 \]
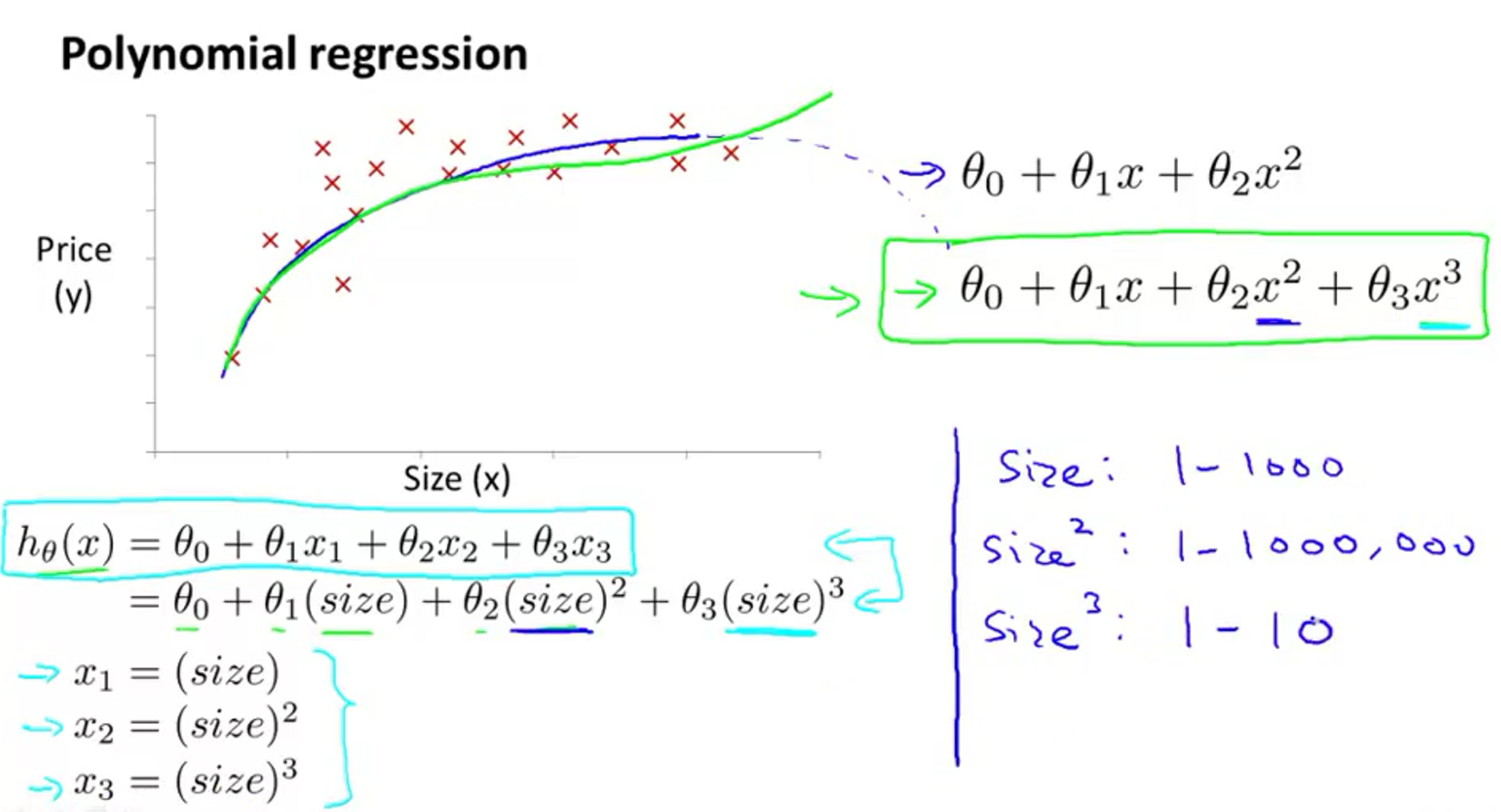
当然可以用\(x_2 = x^2_2, x_3 = x_3^3\)来转化为多变量线性回归。如果使用多项式回归,那么在梯度下降之前,就必须要使用特征缩放。
正规方程
对于一些线性回归问题,使用正规方程方法求解参数\(\theta\),比用梯度下降更好些。代价函数如下 \[ \color{red} {J(\theta_0, \theta_1) = \frac {1}{2m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)}\right)^2} \] 正规方程的思想是函数\(J(\theta)\)对每个\(\theta_j\)求偏导令其等于0,就能得到所有的参数。即\(\frac{\partial J}{\partial \theta_j} = 0\)。
那么设\(X_{m\times(n+1)}\)为数据矩阵(其中包括\(x_0=1\)),\(y\)为标签向量。则通过如下方程可以求得\(\theta\) \[ \theta = (X^TX)^{-1}X^Ty \] 正规方程和梯度下降的比较
| 梯度下降 | 正规方程 |
|---|---|
| 需要特征缩放 | 不需要特征缩放 |
| 需要选择学习率\(\alpha\) | 不虚选择学习率 |
| 需要多次迭代计算 | 一次运算出结果 |
| 特征数量\(n\)很大时,依然适用 | \(n\)太大,求矩阵逆运算代价太大,复杂度为\(O(n^3)\)。\(n\leq10000\)可以接受 |
| 适用于各种模型 | 只适用于线性模型,不适合逻辑回归和其他模型 |
逻辑回归
线性回归有2个不好的问题:直线难以拟合很多数据;数据标签一般是\(0, 1\),但是\(h_\theta(x)\)却可能远大于1或者远小于0。如下图。
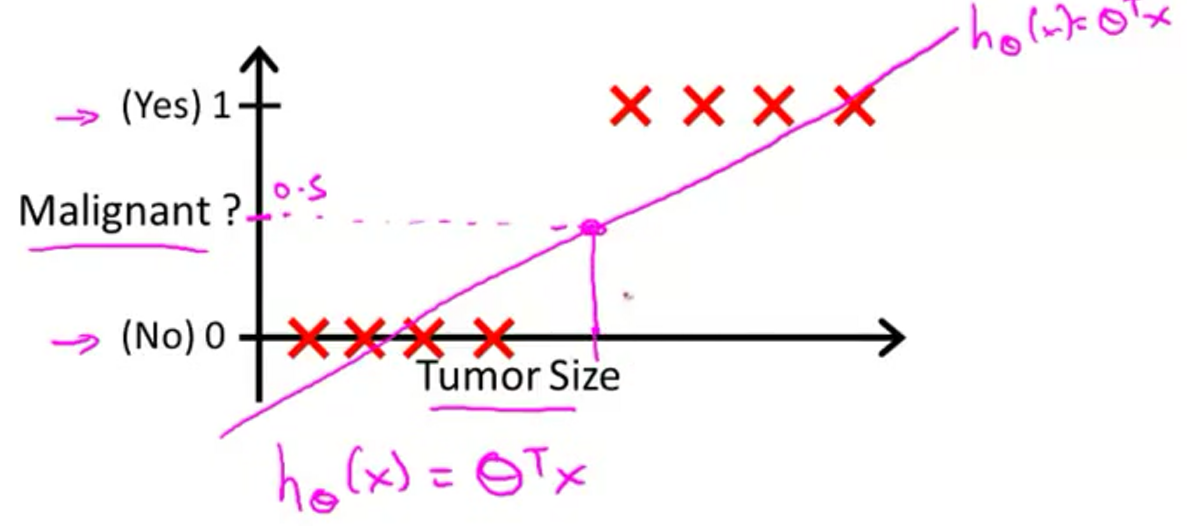
基本模型
逻辑回归是一种分类算法,使得输出预测值永远在0和1之间,是使用最广泛的分类算法。模型如下 \[
h_\theta(x) = g(\theta^Tx), \quad g(z) = \frac{1}{1+e^{-z}}
\] \(g(z)\)的图像如下,也称作Sigmoid函数或者Logistic函数,是S形函数。
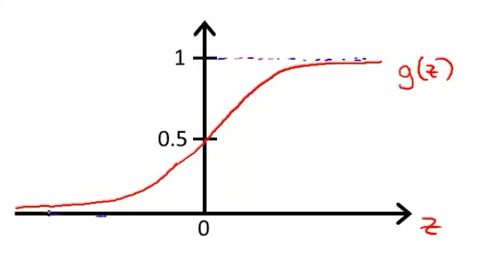
将上面的公式整理后得到逻辑回归的模型 \[ \color{red}{h_\theta(x) = \frac {1}{1+e^{-\theta^Tx}}}, \quad 其中\; \color{red}{0 \le h_\theta(x) \le 1} \] 模型的意义是给出分类为1的概率,即\(h_\theta(x) = P(y=1\mid x; \theta)\)。例如\(h_\theta(x)=0.7\),则分类为1的概率是0.7,分类为0的概率是\(1-0.7=0.3\)。 \[ x的分类预测, y = \begin{cases} 1, \; & h_\theta(x) \ge 0.5, \;即\; \theta^Tx \ge 0\\ 0, \; & h_\theta(x) < 0.5, \; 即 \; \theta^Tx < 0 \\ \end{cases} \]
逻辑回归就是要学到合适的\(\theta\),使得正例的特征远大于0,负例的特征远小于0。
决策边界
线性边界
假设我们有一个模型\(h_\theta(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2)\),已经确定参数\(\theta = (-3, 1, 1)\),即模型\(h_\theta(x) = g(-3+x_1+x_2)\),数据和模型如下图所示

由上可知,分类结果如下 \[
y =
\begin{cases}
1, \, & x_1+ x_2 \ge 3 \\
0, \, & x_1 + x_2 < 3 \\
\end{cases}
\] 那么直线\(x_1+x_2=3\)就称作模型的决策边界,将预测为1的区域和预测为0的区域分隔开来。gg
非线性边界
先看下面的数据

使用这样的模型去拟合数据 \[ h_\theta(x) = g(\theta_0 + \theta_1x_1 + \theta_2x_2 + \theta_3x_1^2 + \theta_4x_2^2) , \; \theta = (-1, 0, 0, 1, 1), \; 即\, \color{red}{h_\theta(x) = g(-1+x_1^2 + x_2^2)} \] 对于更复杂的情况,可以用更复杂的模型去拟合,如\(x_1x_2, x_1x_2^2\)等
代价函数和梯度下降
我们知道线性回归中的代价函数是\(J(\theta_0, \theta_1) = \frac {1}{2m} \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)}\right)^2\),但是由于逻辑回归的模型是\(\color{red}{h_\theta(x) = \frac {1}{1+e^{-\theta^Tx}}}\),所以代价函数关于\(\theta\)的图像就是一个非凸函数,容易达到局部收敛,如下图左边所示。而右边,则是一个凸函数,有全局最小值。

代价函数
逻辑回归的代价函数 \[ \rm{Cost}(h_\theta(x), y) = \color{red}{ \begin{cases} -\log(h_\theta(x)),\; & y=1 \\ -\log(1-h_\theta(x)), \; & y=0 \\ \end{cases} } \] 当实际上\(y=1\)时,若预测为0,则代价会无穷大。当实际上\(y=0\)时,若预测为1,则代价会无穷大。
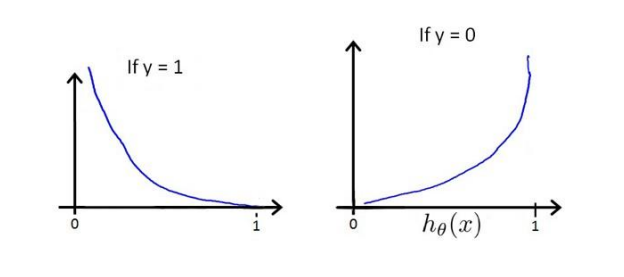
整理代价函数如下 \[ \rm{Cost}(h_\theta(x), y) =\color{red}{ -y \cdot \log(h_\theta(x)) - (1-y) \cdot \log(1- h_\theta(x))} \] 得到所有的\(\color{red}{J(\theta)}\) \[ J(\theta) = -\frac{1}{m} \sum_{i=1}^m \left( y^{(i)}\log h_\theta(x^{(i)}) + (1 - y^{(i)}) \log(1-h_\theta(x^{(i)})) \right) \] 梯度下降
逻辑回归的假设函数估计\(y=1\)的概率 \(\color{red}{h_\theta(x) = \frac {1}{1+e^{-\theta^Tx}}}\)。
代价函数\(\color{red}{J(\theta)}\),求参数\(\theta\)去\(\color{red}{\min \limits_{\theta} J(\theta)}\)
对每个参数\(\theta_j\),依次更新参数 \[ \color{red} {\theta_j = \theta_j -\alpha \cdot \frac{1}{m} \sum_{i=1}^m \left(h_\theta(x^{(i)})-y^{(i)} \right) \cdot x_j^{(i)}} \] 逻辑回归虽然梯度下降的式子和线性回归看起来一样,但是实际上\(h_\theta(x)\)和\(J(\theta)\)都不一样,所以是不一样的。
