基于策略函数的学习方法
强化学习目标
强化学习的目标是学习到一个策略\(\pi_{\theta}(a\mid s)\),来最大化这个策略的期望回报。希望智能体能够获得更多的回报。本质上是策略搜索。 \[ J(\theta) = E_{\tau \sim p_{\theta}(\tau)} [\sum_{t=0}^{T-1}\gamma ^tr_{t+1}] \]
\[ J(\theta) = \int p_{\theta}(\tau) \cdot G(\tau) \, {\rm d}\tau \]
策略搜索本质上是一个优化问题,无需值函数可以直接优化策略。参数化的策略可以处理连续状态和动作。
- 基于梯度的优化
- 无梯度的优化
策略梯度
1. 思想和假设
策略梯度 :是一种基于梯度的强化学习方法。
策略连续可微假设:假设\(\pi_{\theta}(a \mid s)\)是一个关于\(\theta\)的连续可微函数。
2. 优化目标
最大化策略的期望回报。
\[ J(\theta) = \int p_{\theta}(\tau) \cdot G(\tau) \, {\rm d}\tau \]
3. 策略梯度推导
采用梯度上升法来优化参数\(\theta\)来使得\(J(\theta)\)最大。
策略梯度\(\frac{\partial J(\theta)}{\partial \theta}\)的推导如下:
1、参数\(\theta\)的优化方向是总回报\(G(\tau)\)大的轨迹\(\tau\),其概率\(p_\theta(\tau)\)也就越大。 \[ \begin{align} \frac{\partial J(\theta)}{\partial \theta} & = \frac{\partial} {\partial \theta} \int p_{\theta}(\tau) \cdot G(\tau) \, {\rm d}\tau = \int \left(\frac{\partial}{\partial \theta} p_{\theta}(\tau)\right) \cdot G(\tau) \, {\rm d}\tau \\ & = \int \color{blue}{p_{\theta}(\tau)} \cdot \left(\color{blue}{\frac{1} {p_{\theta}(\tau)}}\frac{\partial}{\partial \theta} p_{\theta}(\tau)\right) \cdot G(\tau) \, {\rm d}\tau \\ & = \int p_{\theta}(\tau) \cdot \left( \color{blue}{ \frac{\partial}{\partial \theta} \log p_{\theta}(\tau) }\right) \cdot G(\tau) \, {\rm d}\tau \\ & \triangleq E_{\tau \sim p_{\theta}(\tau)} \left[ \color{blue}{\frac{\partial}{\partial \theta} \log p_{\theta}(\tau)} \cdot G(\tau)\right] \end{align} \] 2、梯度只和策略相关,轨迹的梯度 == 各个时刻的梯度的求和 \[ \begin{align} \frac{\partial}{\partial \theta} \log p_{\theta}(\tau) & = \frac{\partial}{\partial \theta} \log \left( p(s_0) \cdot \prod_{t=0}^{T-1} \underbrace {\pi_{\theta}(a_t \mid s_t) }_{\color{blue}{执行动作}} \underbrace{p(s_{t+1} \mid s_t,a_t)}_{\color{blue}{环境改变}}\right) \\ & = \frac{\partial}{\partial \theta} \log \left( \log p(s_0) + \color{blue}{\sum_{t=0}^{T-1} \log\pi_{\theta}(a_t \mid s_t) }+ \sum_{t=0}^{T-1} \log p(s_{t+1} \mid s_t,a_t) \right) \\ & = \sum_{t=0}^{T-1} \frac{\partial}{\partial \theta} \color{blue}{ \log\pi_{\theta}(a_t \mid s_t)} \end{align} \] 3、策略梯度 == 轨迹的梯度*轨迹的回报 的期望 \[ \begin{align} \frac{\partial J(\theta)}{\partial \theta} & = E_{\tau \sim p_{\theta}(\tau)}\left[ \left(\sum_{t=0}^{T-1} \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \right) \cdot G(\tau)\right] \\ & = E_{\tau \sim p_{\theta}(\tau)}\left[ \left(\sum_{t=0}^{T-1} \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \right) \cdot \left( \color{blue}{G(\tau_{1:k-1}) + \gamma^k \cdot G(\tau_{k:T})}\right) \right] \\ & = E_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t=0}^{T-1} \left(\frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \cdot \gamma^t G(\tau_{t:T})\right) \right] \end{align} \] 其中\(G(\tau_{t:T})\)是从时刻\(t\)作为起始时刻收到的总回报 \[ G(\tau_{t:T}) = \sum_{i=t}^{T-1} \gamma ^{i-t} r_{i+1} \] 4. 总结
\[ \frac{\partial J(\theta)}{\partial \theta} \triangleq E_{\tau \sim p_{\theta}(\tau)} \left[ \color{blue}{\frac{\partial}{\partial \theta} \log p_{\theta}(\tau)} \cdot G(\tau)\right] \]
\[ \frac{\partial}{\partial \theta} \log p_{\theta}(\tau) = \sum_{t=0}^{T-1} \frac{\partial}{\partial \theta} \color{blue}{ \log\pi_{\theta}(a_t \mid s_t)} \]
\[ \begin{align} \frac{\partial J(\theta)}{\partial \theta} & = E_{\tau \sim p_{\theta}(\tau)}\left[ \sum_{t=0}^{T-1} \left(\frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \cdot \gamma^t G(\tau_{t:T})\right) \right] \end{align} \]
REINFORCE算法
期望可以通过采样的方法来近似。对于当前策略\(\pi_\theta\),可以随机游走采集N个轨迹。\(\tau^{(1)},\cdots, \tau^{(N)}\) \[ \begin{align} \frac{\partial J(\theta)}{\partial \theta} & \approx \frac{1}{N}\sum_{n=1}^ N \left[ \sum_{t=0}^{T-1} \left(\frac{\partial}{\partial \theta} \log\pi_{\theta}(a^{(n)}_t \mid s^{(n)}_t) \cdot \gamma^t G(\tau^{(n)}_{t:T})\right) \right] \end{align} \] 可微分策略函数\(\pi_\theta(a\mid s)\),折扣率\(\gamma\),学习率\(\alpha\)
初始化参数\(\theta\), 训练,直到\(\theta\)收敛
1、根据\(\pi_\theta(a\mid s)\)生成一条轨迹 \[ \tau = s_0, a_0, s_1,a_1, \cdots, s_{T-1}, a_{T-1}, s_{T} \] 2、在每一时刻更新参数 (0~T)
- 计算\(G(\tau_{t:T})\)
- \(\theta \leftarrow \theta + \alpha \cdot \gamma^tG(\tau_{t:T}) \cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t)\)
REINFORCE算法缺点:不同路径之间的方差很大,导致训练不稳定;需要根据一个策略采集一条完整的轨迹。

带基准线的REINFORCE算法
值函数作为基准函数,去减小策略梯度的方差
由于不同轨迹之间的方差很大,导致训练不稳定,使用基准函数去减小策略梯度的方差。
1. 减小方差的办法
目标:估计函数\(f\)的期望,同时要减小\(f\)的方差。
方法
- 引入已知期望的函数\(g\)
- \(\hat f = f - \alpha(g - E[g])\)
- 推导可知: \(E[f] = E[\hat f]\)
- 用\(g\)去减小\(f\)的方差, \(D(f)=Var(f)\)
\[ D(\hat f) = D(f) - 2\alpha \cdot \rm{Cov}(f,g) + \alpha^2 \cdot D(g) \]
\[ 令\frac{\partial D(\hat f)}{\partial \alpha} = 0 \quad \to \quad \frac{D(\hat f)}{D(f)} = 1 - \rho^2(f, g) \]
所以,\(f\)和\(g\)的相关性越高,\(D(\hat f)\)越小。
2. 带基准线的REINFORCE算法核心
每个时刻\(t\)的策略梯度 \[ \frac{\partial J_t(\theta)}{\partial \theta} = E_{s_t,a_t}\left[ \alpha \cdot \gamma^tG(\tau_{t:T}) \cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \right] \] 为了减小策略梯度的方差,引入一个和\(a_t\)无关的基准函数\(b(s_t)\),策略梯度为: \[ \frac{\partial \hat J_t(\theta)}{\partial \theta} = E_{s_t,a_t}\left[ \alpha \cdot \gamma^t \left( \color{blue} {G(\tau_{t:T}) - b(s_t)}\right)\cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \right] \] 因为\(b(s_t)\)与\(a_t\)无关,可以证明得到:(使用积分求平均,\(\int_{a_t} \pi_{\theta}(a_t \mid s_t) \,{\rm d} a_t= 1\)) \[ E_{a_t}\left[ b(s_t)\cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \right] = \frac{\partial}{\partial \theta} (b(s_t) \cdot 1) = 0 \] 所以得到:\(\frac{\partial J_t(\theta)}{\partial \theta} = \frac{\partial \hat J_t(\theta)}{\partial \theta}\)
4. 基准函数的选择
为了减小策略梯度的方差,希望\(b(s_t)\)与\(G(\tau_{t:T})\) 越相关越好,所以选择\(b(s_t) = V(s_t)\)(值函数)。
1、可学习的函数\(V_{\phi}(s_t)\)来近似值函数,类似于Q网络 \[ \phi^* = \arg \min_{\phi} \left(V(s_t) - V_{\phi}(s_t)\right)^2 \] 2、蒙塔卡罗方法进行估计值函数 也就是增量计算Q(s,a)嘛。
5. 带基准线的REINFORCE算法步骤
输入
- 状态空间和动作空间,\(\cal {S,A}\)
- 可微分的策略函数\(\pi_\theta(a \mid s)\)
- 可微分的状态值函数\(V_{\phi}(s_t)\)
- 折扣率\(\gamma\),学习率\(\alpha, \beta\)
随机初始化参数\(\theta, \phi\)
不断训练,直到\(\theta\)收敛
1、根据策略\(\pi_\theta(a\mid s)\)生成一条完整轨迹 :\(\tau = s_0, a_0, s_1,a_1, \cdots, s_{T-1}, a_{T-1}, s_{T}\)
2、在每一时刻更新参数
计算当前时刻的轨迹回报\(G(\tau_{t:T})\) ,再利用基准函数(值函数)进行修正,得到\(\delta\) \[
\delta \leftarrow G(\tau_{t:T}) - V_{\phi} (s_t)
\] 更新值函数\(V_\phi(s)\)的参数\(\phi\) \[
\phi \leftarrow \phi + \beta \cdot \delta \cdot \frac{\partial}{ \partial \phi} V_{\phi}(s_t)
\] 更新策略函数\(\pi_\theta(a \mid s)\)的参数\(\theta\) \[
\theta \leftarrow \theta + \alpha \cdot \gamma^t\delta \cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t)
\] 缺点: 需要根据策略采集一条完整的轨迹。

Actor-Critic算法
思想
演员-评论员算法是一种结合策略梯度和时序差分学习的强化学习方法。
开始,演员随机表演,评论员随机打分;不断学习,评论员评分越来越准,演员的动作越来越好。
- 演员:策略函数\(\pi_\theta(s,a)\),学习一个策略来得到尽可能高的回报
- 评论员:值函数\(V_\phi(s)\),评估当前策略函数(演员)的好坏
演员
根据\(s\)和策略\(\pi_\theta(a\mid s)\),执行动作\(a\),环境变为\(s^\prime\),得到奖励\(r\)
评论员
根据真实奖励\(r\)和之前的标准,打分(估计回报):\(r + \gamma V_\phi(s^\prime)\) ,再调整自己的打分标准\(\phi\)。\(\min_{\phi} \left(\hat G(\tau_{t:T}) - V_{\phi}(s_{t}) \right)^2\)
使评分更加接近环境的真实回报。
演员
演员根据评论的打分,调整自己的策略\(\pi_\theta\),争取下次做得更好。
优点:可以单步更新参数,不需要等到回合结束才进行更新。
值函数的三个功能
1. 估计轨迹真实回报(打分) \[ \hat G(\tau_{t:T}) = r_{t+1} + \gamma V_{\phi}(s_{t+1}) \] 2. 更新值函数参数\(\phi\) (调整打分标准) \[ \min_{\phi} \left(\hat G(\tau_{t:T}) - V_{\phi}(s_{t}) \right)^2 \] 3. 更新策略参数\(\theta\)时,作为基函数来减少策略梯度的方差(调整策略) \[ \theta \leftarrow \theta + \alpha \cdot \gamma^t \left( G(\tau_{t:T}) - V_{\phi} (s_t)\right) \cdot \frac{\partial}{\partial \theta} \log\pi_{\theta}(a_t \mid s_t) \]
算法实现步骤
输入
- 状态空间和动作空间,\(\cal {S,A}\)
- 可微分的策略函数\(\pi_\theta(a \mid s)\)
- 可微分的状态值函数\(V_{\phi}(s_t)\)
- 折扣率\(\gamma\),学习率\(\alpha >0, \beta>0\)
随机初始化参数\(\theta, \phi\)
迭代直到\(\theta\)收敛,初始状态\(s\), \(\lambda=1\)
从s开始,直到\(s\)为终止状态
1、状态s,选择动作\(a = \pi_\theta(a\mid s)\)
2、执行动作\(a\),得到即时奖励\(r\)和新状态\(s^\prime\)
3、利用值函数作为基函数计算\(\delta\),\(\delta \leftarrow r + \gamma V_{\phi}(s^\prime) - V_{\phi}(s)\)
4、更新值函数:\(\phi \leftarrow \phi + \beta \cdot \delta \cdot \frac{\partial V_{\phi}(s)}{\partial \phi}\)
5、更新策略函数:\(\theta \leftarrow \theta + \alpha \cdot \lambda \delta \cdot \frac{\partial }{\partial \theta} \log \pi_\theta(a\mid s)\)
6、更新折扣率和状态:\(\lambda \leftarrow \lambda \cdot \gamma, \quad s \leftarrow s^\prime\)

强化学习算法总结
方法总览
1. 通用步骤
- 执行策略,生成样本
- 估计回报
- 更新策略
2. 值函数与策略函数的比较
值函数的方法
策略更新,导致值函数的改变比较大,对收敛性有一定的影响
策略函数的方法
策略更新,更加平稳。
缺点:策略函数的解空间很大,难以进行充分采样,导致方差较大,容易陷入局部最优解。
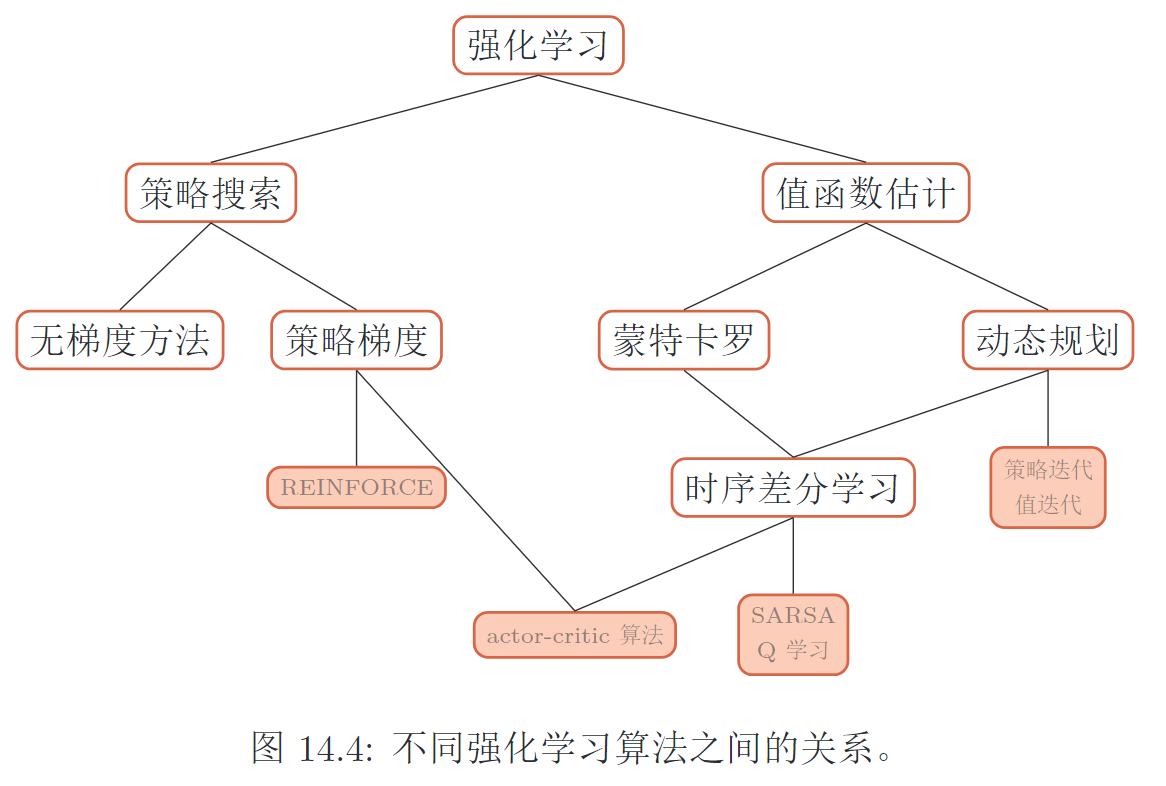
四个典型方法

与监督学习的区别
| 强化学习 | 监督学习 | |
|---|---|---|
| 样本 | 与环境进行交互产生样本,进行试错学习 | 人工收集并标注 |
| 反馈 | 只有奖励,并且是延迟的 | 需要明确的指导信息(每个状态对应一个动作) |
