卷积神经网络
全连接网络的两个问题：
- 参数太多：训练效率低、容易过拟合
- 局部不变形特征：全连接很难提取出图片的不变性特征
三个特性
1. 局部性
图片特征只在局部。图片特征决定图片类别，这些图片特征在一些局部的区域中。
局部连接。
2. 相同性
用同样的检测模式去检测不同图片的相同特征。只是这些特征出现在图片的不同位置。
参数共享。
3. 不变性
对于一张大图片，进行下采样，图片的性质基本保持不变。
下采样保持不变性。
卷积
- 一维卷积：卷积核、步长、首位0填充
- 三种卷积：窄卷积、宽卷积、等长卷积
- 二维卷积
1. 一维卷积
- 卷积核：参数\([1, 0, -1]\)就是一个
卷积核或滤波器 - 步长：卷积核滑动的间隔
- 零填充：在输入向量两端进行补零
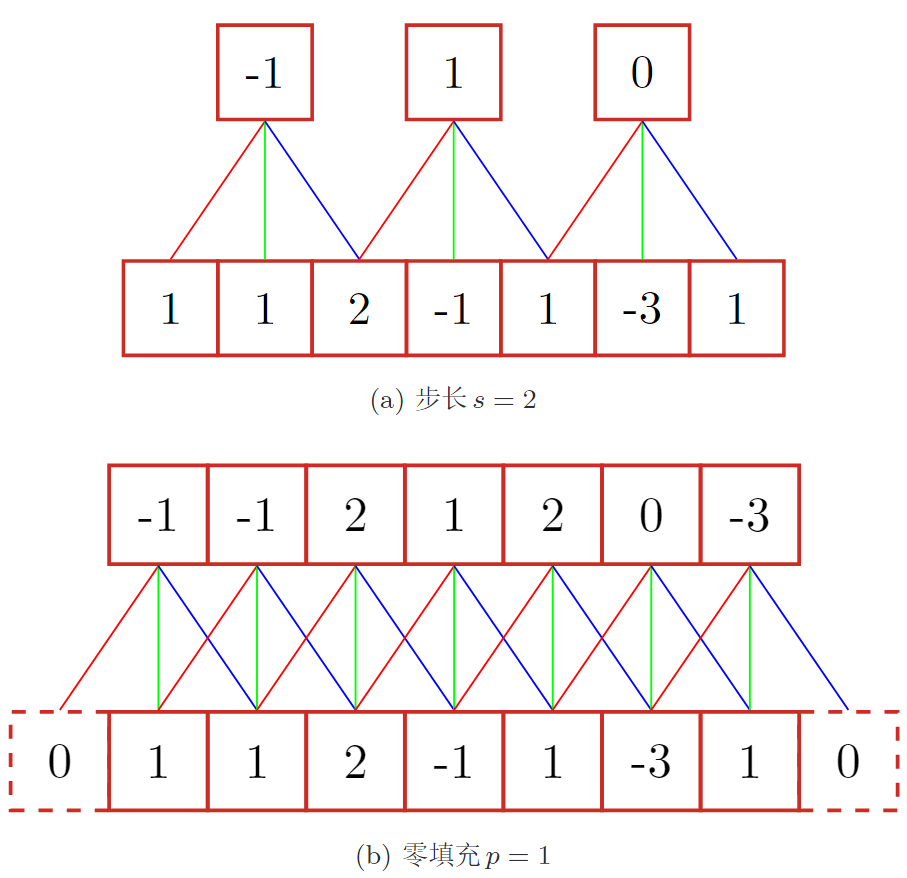
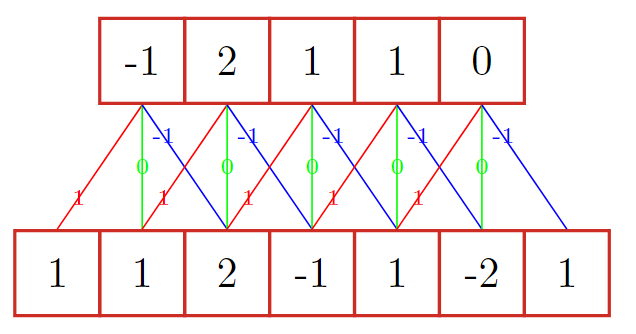2. 三种卷积
输入n，卷积大小m，步长s，输入神经元各两端填补p个0
- 窄卷积：
s=1，不补0，输出长度为n-m+1 - 宽卷积：
s=1，两端补0，\(p=m-1\)， 输出长度为n+m-1 - 等长卷积：
s=1，两端补0，\(p=\frac{m-1}{2}\)， 输出长度为n
一般卷积默认为窄卷积。
3. 二维卷积
输入一张图片（假设深度为1），\(X \in \mathbb R^{M \times N}\)， 卷积核\(W \in \mathbb R ^{m \times n}\) ，则卷积（互相关代替）结果为： \[
y_{ij} = \sum_{u=1}^m \sum_{v=1}^n w_{uv} x_{i+u-1, j+v-1}
\] 
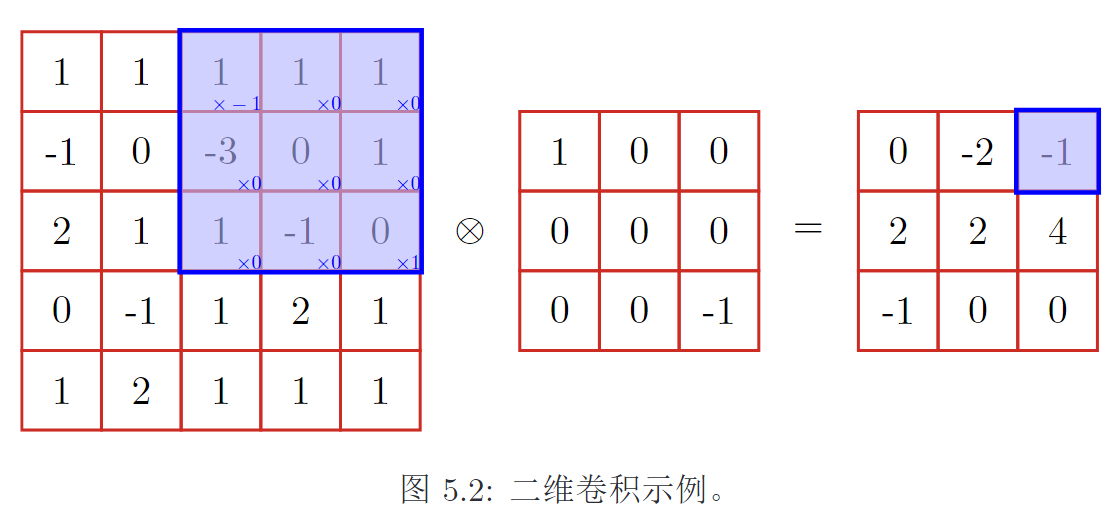
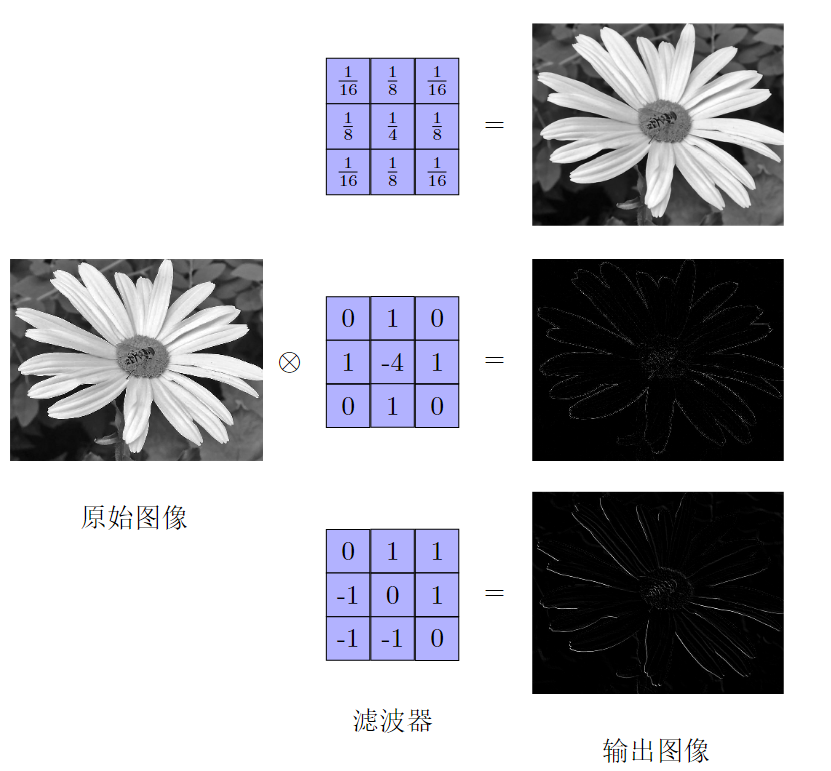
一个卷积核提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器。
卷积后的结果称为特征映射（feature map）。
卷积层
- 一个卷积核
\(W_p \in \mathbb R ^{m \times n \times D}\)， 对D个通道做卷积，结果相加求和，过激活函数，得到一个特征图\(Y^p \in\mathbb R^{M^\prime \times N^\prime}\)
- 多个卷积核：得到P个特征图
输入图片(feature map)是\(X \in \mathbb R^{M \times N \times D}\)，深度是D
1. 一个卷积核
- 用1个卷积核\(W_p \in \mathbb R ^{m \times n \times D}\)（实际上是D个\(\mathbb R^{m\times n}\)）去卷积这张图片（所有深度）
- 对各个深度的卷积结果进行相加求和，再加上偏置
- 过激活函数，输出最终的FM，是\(Y^p\)
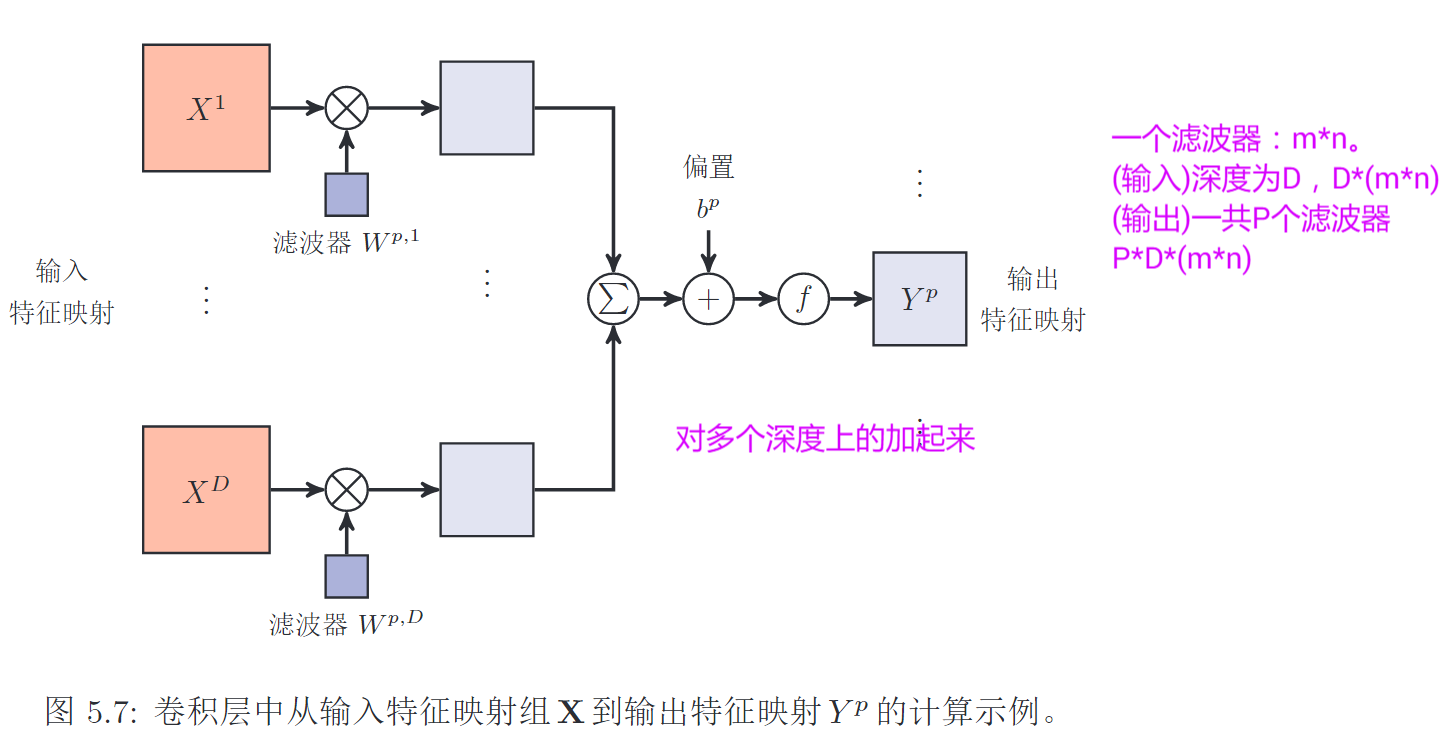
2. 多个卷积核
多个卷积核可以提取出多种不同的特征。输入图片是\(X \in \mathbb R^{M \times N \times D}\)，
- 有P个不同的卷积核\(W_p \in \mathbb R ^{m \times n \times D}\)， 实际上是四维的[m, n, D, P]，后两维是
in_channel、out_channel - 输出P个特征图\(\mathbb R^{M^\prime \times N^\prime \times P}\)
- 对每一个卷积核\(W \in \mathbb R ^{m \times n \times D}\)，对D个深度\(\mathbb R ^{m \times n}\)分别做卷积，对D个卷积结果进行求和相加，经过激活函数，得到一个特征图 \(Y^p \in\mathbb R^{M^\prime \times N^\prime}\)
- 一共需要\(P \times D \times (m \times n) + P\)个参数
卷积代替全连接
- 局部连接：卷积核只与输入的一个局部做连接，计算出FM中的一个值，局部性
- 权值共享：同一个卷积核与图片的各个位置进行连接，权值是一样的，提取出同样的特征
1. 局部连接
- 卷积层的神经元只与输入数据的一个局部区域做连接
- 因为图片的局部性，图片的特征在局部
- FM中的每一个值，只与输入的局部相关。而不是与所有的相关
2. 权值共享
- 一个卷积核会分多次对输入数据的各个部分做卷积操作
- 对每个部分的连接参数实际上是相同的，因为是同一个卷积核
- 因为图片的相同性，同样的卷积核可以检测出相同的特征，只是特征在不同的位置
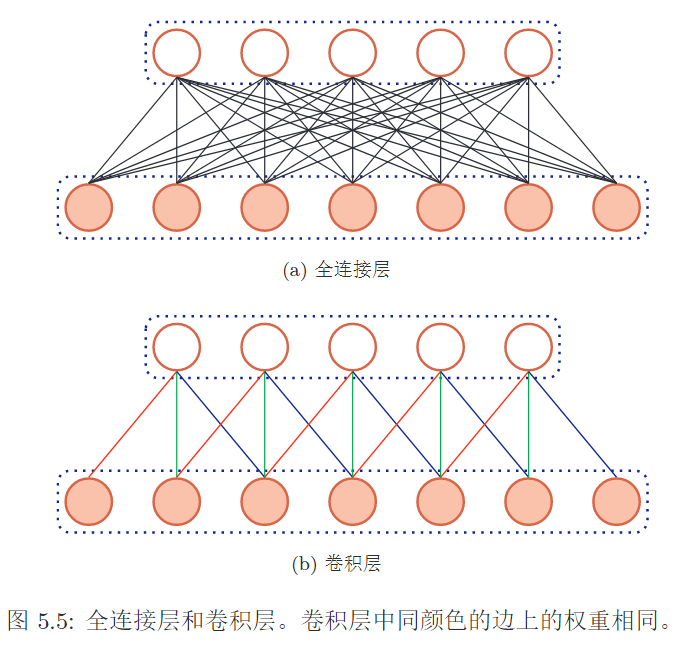
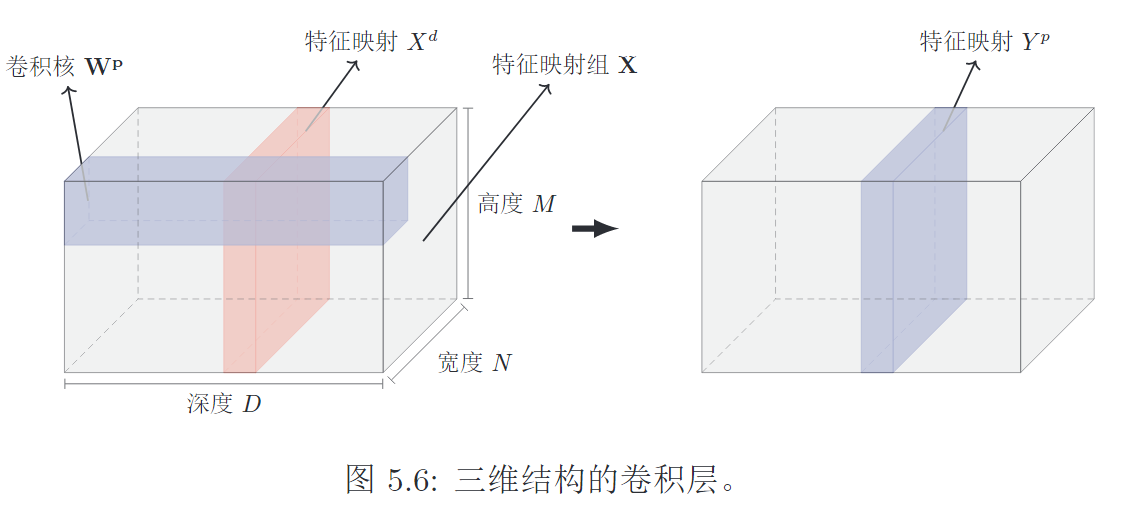
汇聚层
- 卷积层的不足：FM的维数很高
- 汇聚层的作用：选择特征、降低特征数量、减少参数数量、避免过拟合
- 两种汇聚方式：最大和平均。
1. 卷积层的不足
- 减少网络连接数量
- 但是FM中的神经元个数依然很多
- 如果直接接分类器全连接，则维数会很高，容易过拟合
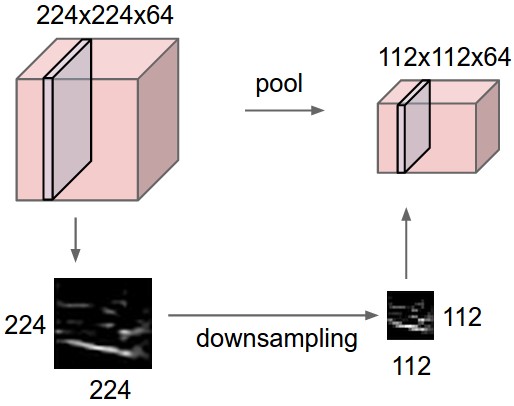
2. 汇聚层的作用
汇聚层(pooling layer)，也作子采样层(subsampling layer)。作用是：
- 进行特征选择
- 降低特征数量
- 进而减少参数数量、避免过拟合
- 拥有更大感受野，大图片缩小，保持
不变性
3. 两种汇聚方式
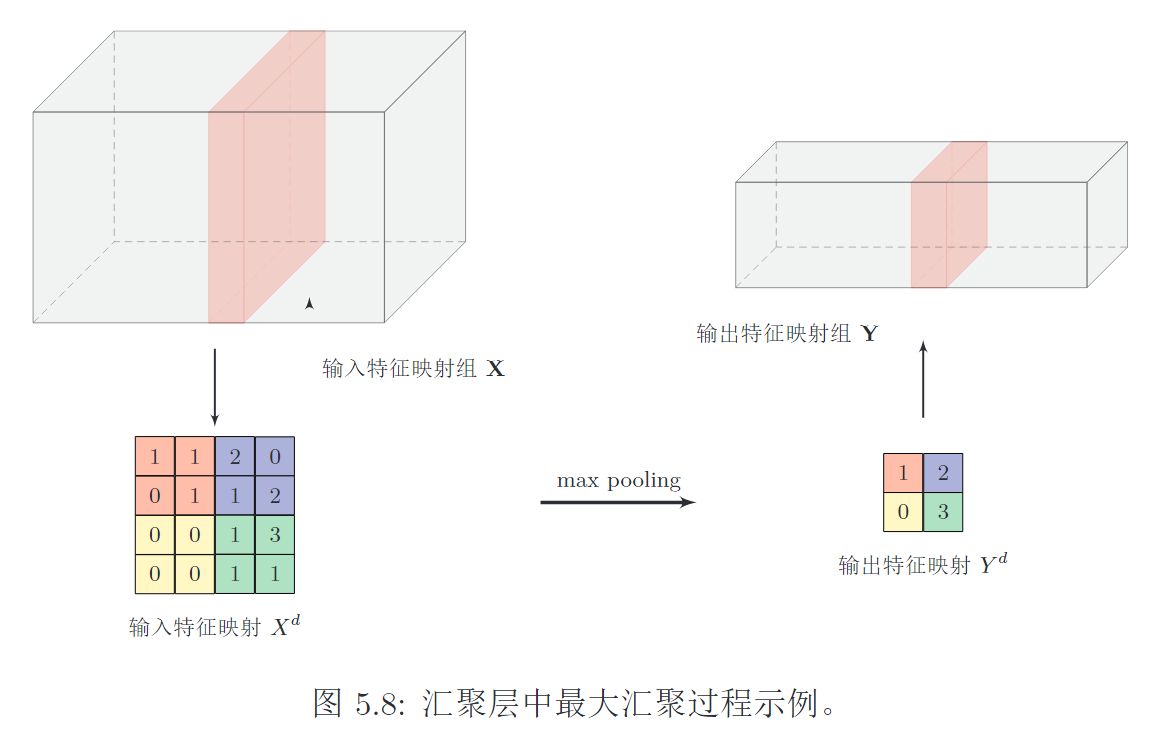
- 最大汇聚：一个区域内所有神经元的最大值
- 平均汇聚：一个区域内所有神经元的平均值
过大采样区会急剧减少神经元的数量，造成过多的信息损失！
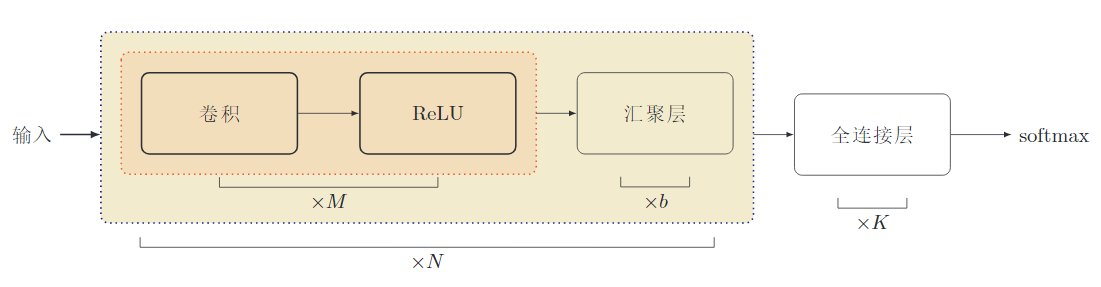
典型的卷积网络结构
由多个卷积块组成，一个卷积块：
- 连续2~5个卷积层，ReLU激活函数
- 0~1个汇聚层
目前，趋向于使用更小的卷积核，比如\(1\times 1, 3 \times 3\)。汇聚层的比例也逐渐降低，趋向于全卷积网络。
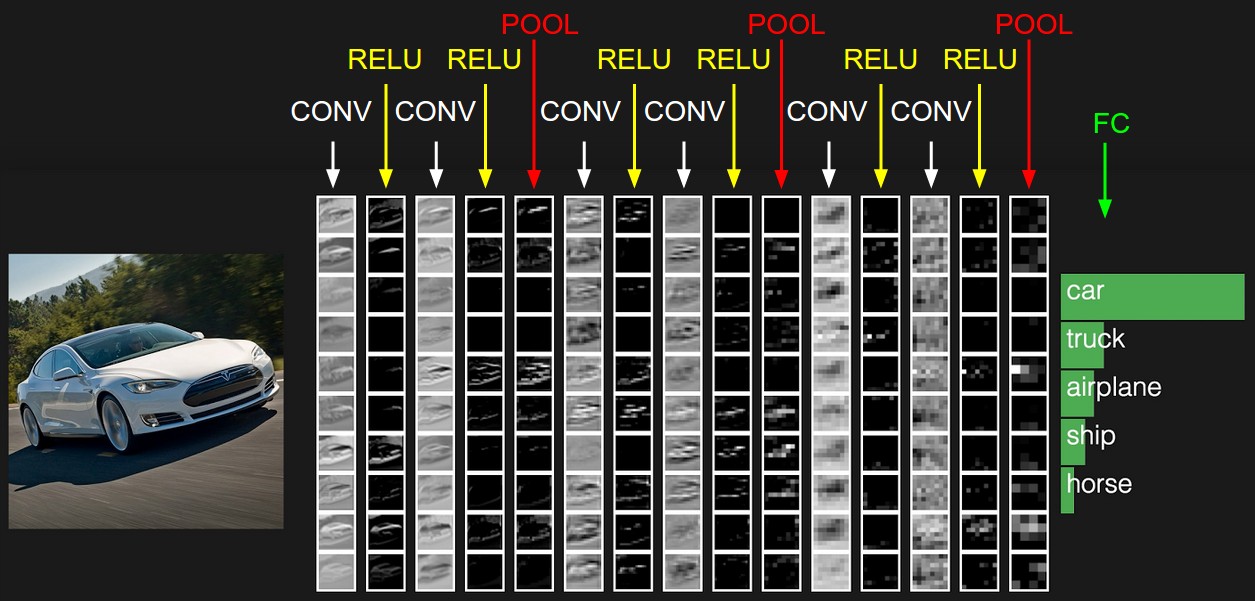
常见卷积网络
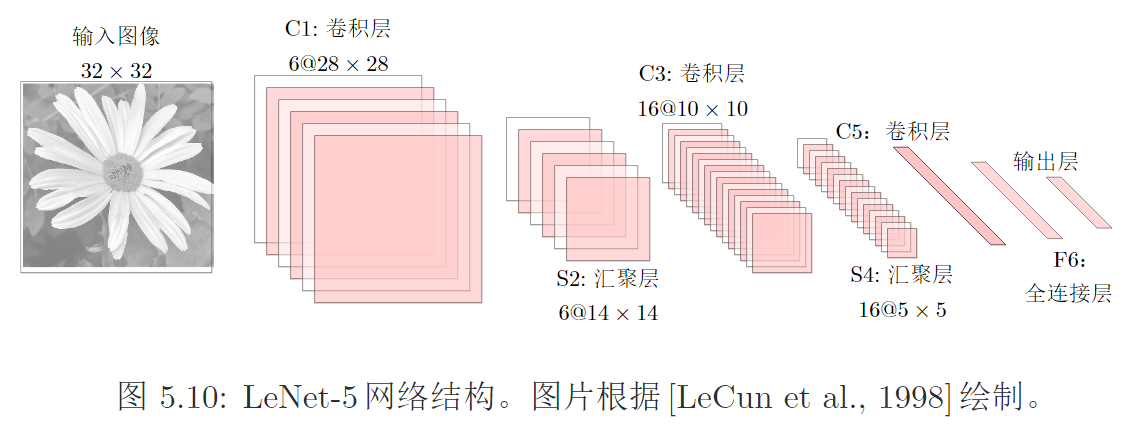
LeNet
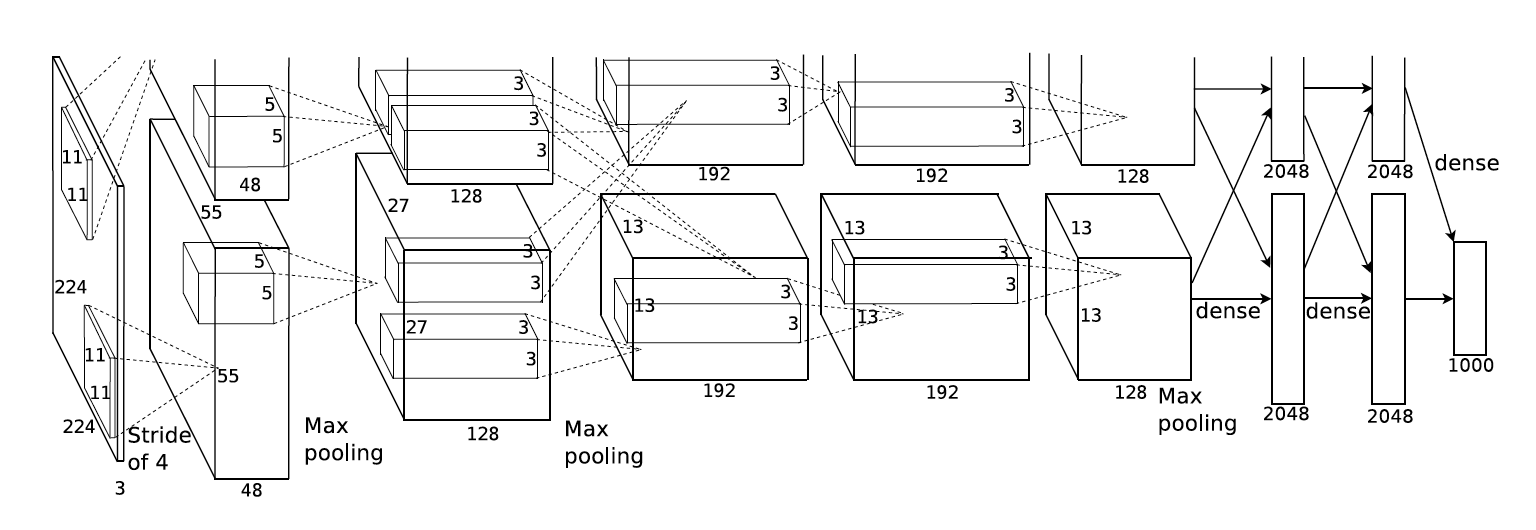
Alex Net
使用ReLU作为非线性激活函数、Dropout防止过拟合、数据增强提高模型准确率。
AlexNet分组卷积
- 对所有通道进行分组，进行分组卷积，执行标准卷积操作
- 在最后时刻才使用两个全连接融合通道的信息
- 降低了模型的泛化能力
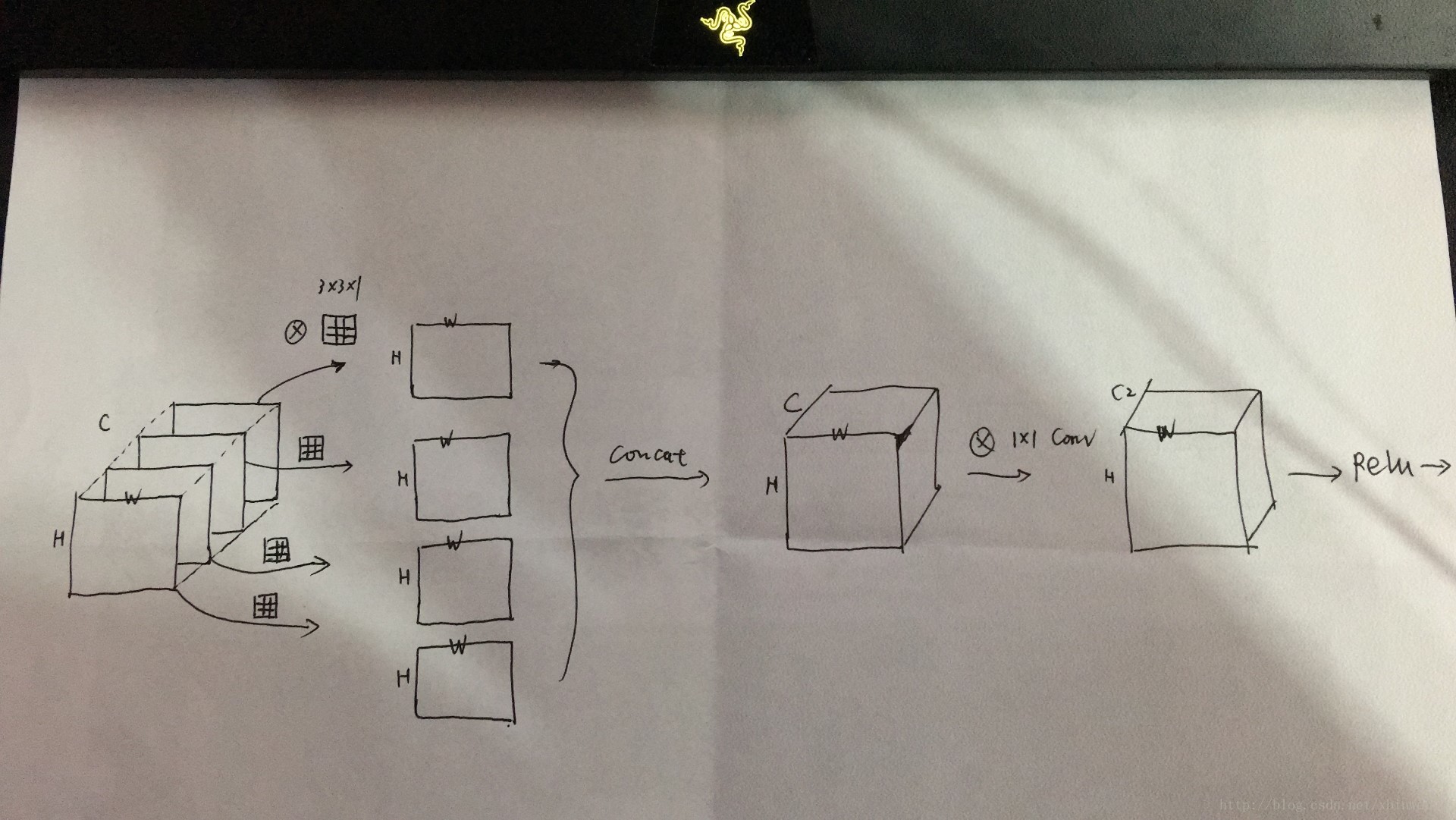
Inception Net
如何选择卷积核大小非常关键：
- 一个卷积层同时使用多种尺寸的卷积核
- 先过\(1\times 1\)卷积减少卷积层参数量
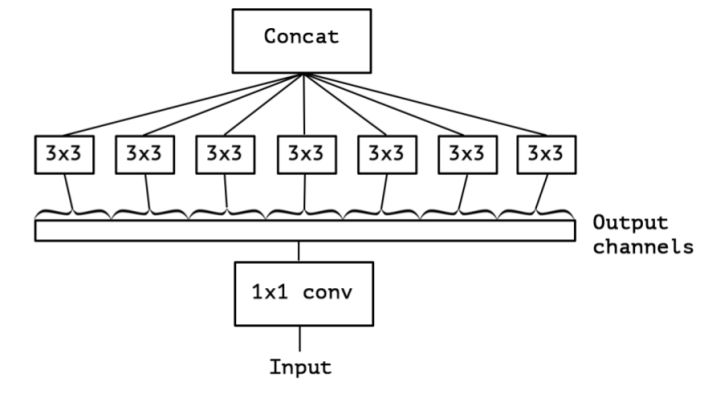
Inception Net由多个Inception模块堆叠而成。一个Inception同时使用\(1\times 1\)、\(3\times 3\)、\(5\times 5\) 的卷积，如下：
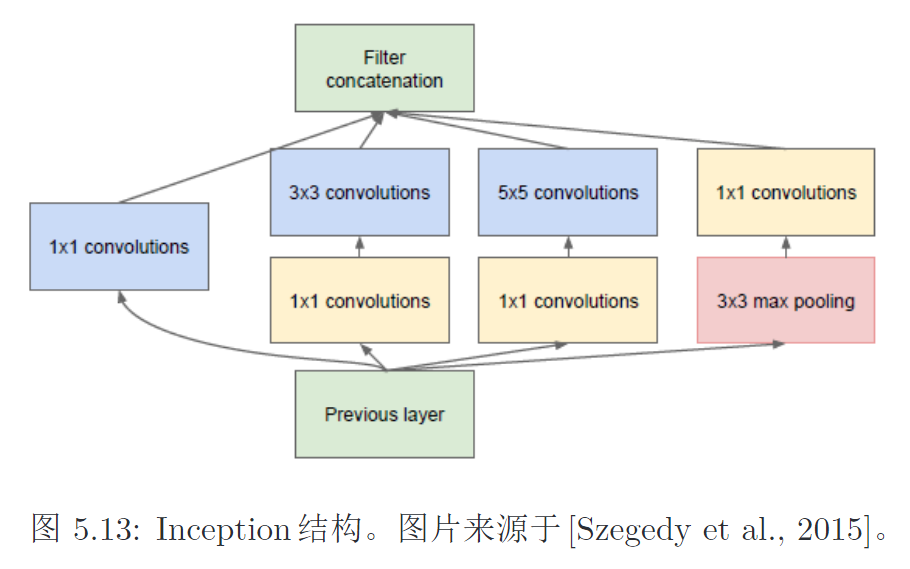
\(3\times 3\) 、\(5\times 5\) 卷积前，先进行\(1\times 1\)卷积的作用：
- 减少输入数据的深度
- 减少各个深度的冗余信息，先进行一次特征抽取
后续还有各种各样的Inception Net，最终演变成Xception Net。
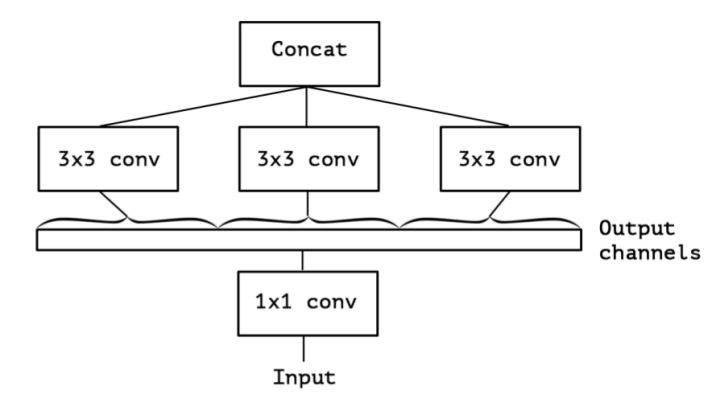
Inception Net的极限就是，对每个channel做一个单独的卷积。
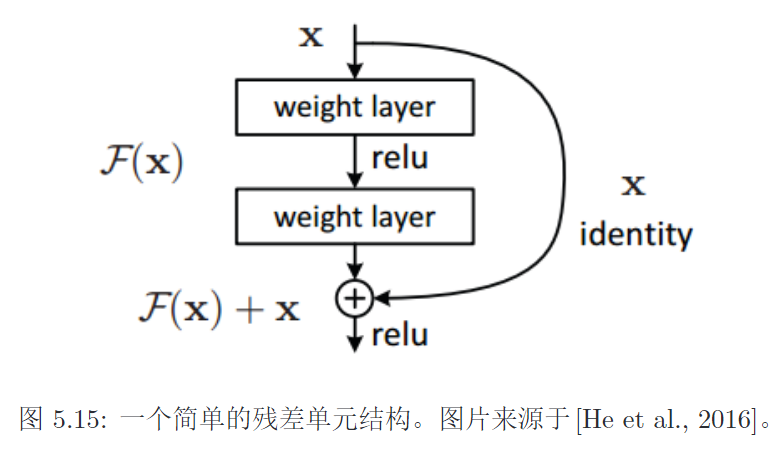
Res Net
越深的网络可以用ResNet来训练。ResNet可以很深的原因
残差连接通过给非线性的卷积层增加直连边的方式
- 来提高信息的传播效率
- 可以减小梯度消失问题
Xception
卷积需要同时考虑所有通道吗？
输入图片(feature map)是\(X \in \mathbb R^{M \times N \times D}\)，深度是D
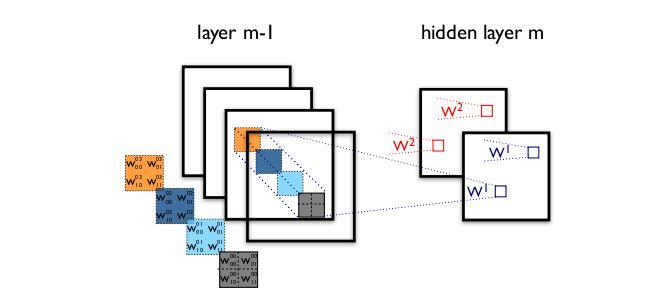
1. 传统卷积核会同时考虑所有通道
- 传统1个卷积核会对所有channel的FM做同样的卷积
- 得到D个卷积结果
- 再对D个卷积结果进行相加求过激活函数得到一个FM
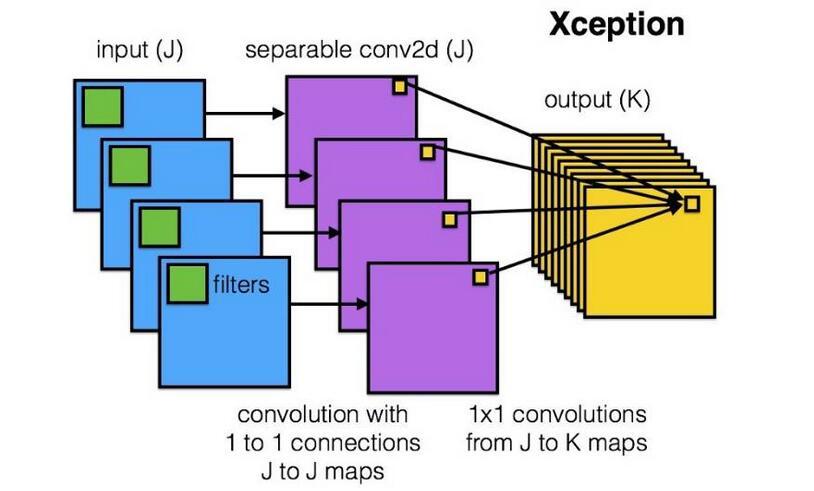
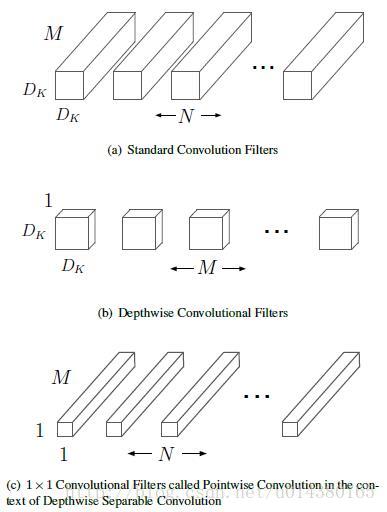
2. 深度可分离卷积核
Depth Separable Convolution
输入数据有D个FM，输出P个FM。深度可分离卷积(DepthWise Convolution) 如下：
- 对\(X\)的每个channel，分别做一个单独的卷积，得到D个新的FM
- 对D个新的FM，做\(1\times 1\)的传统卷积(
PointWise Convolution)，\(P \times D \times (1 \times 1)\) - 最终输出P个FM （通道数变换）
卷积操作不一定需要同时考虑通道和区域。可分离卷积。
3. 可分离卷积参数大大减小
输入通道\(D=3\)，输出通道\(P=256\)，卷积核大小为\(3 \times 3\)
- 传统卷积参数：\(256 \times 3 \times (3 \times 3) = 6912\)
- DepthWise卷积参数：\(3 \times 3 \times 3 +256 \times 3 \times (1 \times 1) =795\)， 降低九分之一
同时，效果更好。
Shuffle Net
1. AlexNet分组卷积
- 对所有通道进行分组，进行分组卷积，执行标准卷积操作
- 在最后时刻才使用全连接融合通道的信息
- 降低了模型的泛化能力
2. ShuffleNet 分组卷积
ShuffleNet = 分组卷积（通道分组）+ 深度可分离卷积（Depthwise+PointWise）
对通道进行分组卷积时
- 每一个组执行深度可分离卷积，而不是标准传统卷积
- 每一次层叠分组卷积时，都进行channel shuffle
- 实际上每个组各取一个也能实现shuffle
SENet
Inception、ShuffleNet等网络中，对所有通道产生的特征都是不分权重直接相加求和的。
为什么所有通道的特征对模型的作用是相等的呢？
总结
1. 卷积核
- 大卷积核用多个小卷积核代替
- 单一尺寸卷积核用多尺寸卷积核代替
- 固定形状卷积核趋于用可变形卷积核
- 使用\(1\times 1\)卷积核
2. 卷积层通道
- 标准卷积使用深度可分离卷积代替
- 使用分组卷积
- 分组卷积前使用channel shuffle
- 通道加权计算
3. 卷积层连接
- 使用skip connection，让模型更深
- densely connection，使每一层都融合其它层的特征输出
