强化学习定义
概览
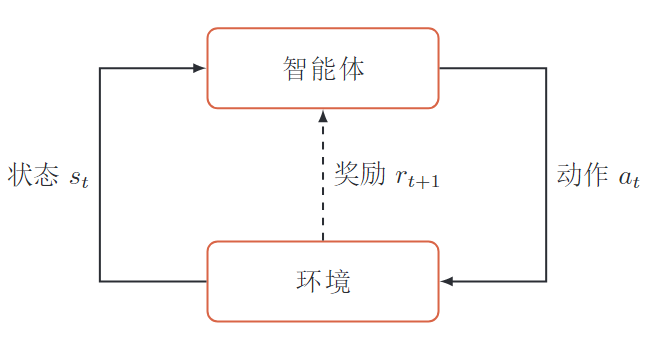
强化学习是指一个智能体从与环境的交互中不断学习去完成特定的目标。
强化学习不需要给出正确策略作为监督信息,只需要给出策略的(延迟)回报,并通过调整策略来取得最大化的期望回报。
- 智能体、环境
- 环境状态\(s\),智能体的动作\(a\),智能体的策略\(\pi(a\mid s)\),状态转移概率\(p(s_{t+1}\mid s_t, a_t)\),即使奖励\(r(s, a, s \prime)\)
智能体和环境
智能体
- 感知环境的状态和反馈的奖励,进行学习和决策
决策:根据 -- 环境状态 -- 做出不同的动作学习: 根据 -- 反馈奖励 -- 调整策略
环境
- 智能体外部的所有事物
- 收到 -- 智能体的动作 -- 改变状态
- 给 -- 智能体 -- 反馈奖励
5个基本要素
状态\(s\)
环境的状态,状态空间\(\mathcal S\), 离散/连续
动作\(a\)
智能体的行为,动作空间\(\mathcal A\), 离散/连续
策略\(\pi(a\mid s)\)
智能体 根据 -- 环境状态s -- 决定下一步的动作a 的函数
状态转移概率\(p(s \prime \mid s, a)\)
根据 -- 当前状态\(s\)和智能体的动作\(a\) -- 环境状态变为\(s \prime\)的概率
即时奖励\(r(s, a, s\prime)\)
环境给智能体的奖励,标量函数。根据 -- 环境当前状态 、智能体执行的动作、环境新状态
智能体的策略
\(\pi(a \mid s)\) 智能体根据环境状态决定下一步的动作。分为确定性策略和随机性策略。 \[
\pi(a\mid s) \triangleq p(a\mid s) , \quad \quad \sum_{a \in \mathcal A} \pi(a\mid s) = 1
\] 
马尔科夫决策过程
- 马尔可夫过程,\(p(s_{t+1}\mid s_t)\)
- 马尔可夫决策过程,\(p(s_{t+1} \mid s_t, a_t)\)
- 轨迹,给初始状态,智能体与环境的一次交互过程
马尔可夫过程
状态序列\(s_0, s_1, \cdots, s_t\)具有马尔可夫性,\(s_{t+1}\)只依赖于\(s_t\) \[ p(s_{t+1}\mid s_t, \cdots, s_0) = p(s_{t+1} \mid s_t) \] ## 马尔可夫决策过程
\(s_{t+1}\)依赖于\(s_t\)和\(a_t\), 即环境新状态依赖于当前状态和当前智能体的动作。 \[
p(s_{t+1} \mid s_t, a_t, \cdots, s_0, a_0) = p(s_{t+1}\mid s_t, a_t)
\] 智能体与环境的交互是一个马尔可夫决策过程。
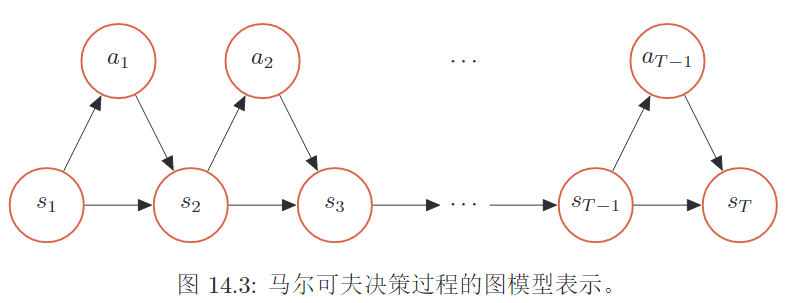
轨迹
给定策略\(\pi(a\mid s)\), 轨迹是智能体与环境的一次交互过程,是一个马尔可夫决策过程,如下: \[ \tau = s_0, a_0, s_1, r_1, \cdots, s_{T-1}, a_{T-1}, s_{T}, r_{T} \] 其中\(r_t = r(s_{t-1}, a_{t-1}, s_t)\)是时刻\(t\)的即时奖励。
轨迹的概率
- 初始状态
- 所有时刻概率的乘积
- 智能体执行动作,环境更新状态
\[ p(\tau) = p(s_0) \prod_{t=0}^{T-1}\pi(a_t \mid s_t) p(s_{t+1} \mid s_t, a_t) \]
目标函数
- 一个轨迹的总回报。\(G(\tau) = \sum_{t=0}^{T-1} r_{t+1}\)
- 一个策略的期望回报。\(E_{\tau \sim p(\tau)} [G(\tau)]\)。 所有轨迹的回报的期望
- 强化学习的目标。学一个策略\(\pi_{\theta}(a \mid s)\), 最大化这个策略的期望回报
轨迹的总回报
1. 某一时刻的奖励
\(r_t = r(s_{t-1}, a_{t-1}, s_t)\)是\(t\)时刻, 环境给智能体的奖励。
给定策略\(\pi(a\mid s)\), 智能体与环境一次交互过程(回合,试验)为轨迹\(\tau\)
2. 一条轨迹的总回报
总回报是一条轨迹所有时刻的累积奖励和。 \[ G(\tau) = \sum_{t=0}^{T-1} r(s_{t-1}, a_{t-1}, s_t) = \sum_{t=0}^{T-1} r_{t+1} \] 3. 一条轨迹的折扣回报
折扣回报引入折扣率,降低远期回报的权重(T无限大时)。 \[
G(\tau) = \sum_{t=0}^{T-1} \gamma^t r_{t+1}, \quad \quad \gamma \in [0, 1]
\] 折扣率\(\gamma\)
- \(\gamma \sim 0\), 在意短期回报
- \(\gamma \sim 1\), 在意长期回报
策略的期望回报
给一个策略\(\pi(a\mid s)\), 有多个轨迹。
一个策略的期望回报:该策略下所有轨迹总回报的期望值。 \[
E_{\tau \sim p(\tau)} [G(\tau)] =E_{\tau \sim p(\tau)} [\sum_{t=0}^{T-1}r_{t+1}]
\]
强化学习的目标
强化学习的目标是学习到一个策略\(\pi_{\theta}(a\mid s)\),来最大化这个策略的期望回报。希望智能体能够获得更多的回报。 \[ J(\theta) = E_{\tau \sim p_{\theta}(\tau)} [\sum_{t=0}^{T-1}\gamma ^tr_{t+1}] \]
值函数
- 状态值函数。\(V^\pi(s)\), 初始状态为s,执行策略\(\pi\)得到的期望回报。
- 贝尔曼方程迭代计算值函数
- 状态-动作值函数。\(Q^\pi(s, a)\), 初始状态为s,进行动作a,执行策略\(\pi\)得到的期望回报
- V函数与Q函数的关系。\(V^\pi(s) = E_{a \sim \pi(a \mid s)}[Q^\pi(s, a)]\)
- 值函数的作用。评估策略\(\pi(a \mid s)\), 对好的动作a(\(Q^\pi(s, a)\)大 ),增大其概率\(\pi(a \mid s)\)
状态值函数
状态值函数\(V^\pi(s)\)是初始状态为\(s\),执行策略\(\pi\)得到的期望回报。(因为有多个轨迹,每个轨迹的初始状态都是\(\tau_{s_0} = s\)) \[ V^\pi(s) = E_{\tau \sim p(\tau)} [\sum_{t=0}^{T-1}r_{t+1} \mid \tau_{s_0} = s] \]
贝尔曼方程计算值函数
当前状态的值函数,可以通过下个状态的值函数进行递推计算。
核心:\(V^\pi(s) \sim r(s, a, s \prime) + V^\pi(s\prime)\)。 有动态规划的意思
- 关键在于状态转移:\(s \sim s\prime\)
- 选动作、选新状态 : \(s \sim a\), \(s, a \sim s\prime\)
- 策略\(\pi(a\mid s)\) 和状态转移概率\(p(s\prime \mid s, a)\)
- 对这两层可能性的所有值函数,求期望即可
给定策略\(\pi(a\mid s)\)、状态转移概率\(p(s\prime \mid s, a)\)、奖励\(r(s, a, s\prime)\), 迭代计算值函数: \[
V^\pi(s) = E[ r(s, a, s\prime) + \gamma V^\pi(s\prime)]
\]
V函数的贝尔曼方程 \[ V^\pi(s) = E_{a \sim \pi(a \mid s)}E_{s\prime \sim p(s\prime \mid s, a)}[ r(s, a, s\prime) + \gamma V^\pi(s\prime)] \]
状态-动作值函数
状态-动作值函数是 初始状态为\(s\)并进行动作\(a\), 执行策略\(\pi\)得到的期望总回报。 也称为Q函数。 \[
Q^\pi(s, a) = E_{s\prime \sim p(s\prime \mid s, a)} [r(s, a, s\prime) + \gamma V^\pi(s\prime)]
\] Q函数的贝尔曼方程 \[
Q^\pi(s, a) = E_{s\prime \sim p(s\prime \mid s, a)} [r(s, a, s\prime) +
\gamma E_{a\prime \sim \pi(a\prime \mid s\prime)}[Q^\pi(s\prime, a\prime)]]
\] ## V函数与Q函数
\(V(s)\)函数要 先确定动作\(s \sim a\), 再确定新状态\(s, a \sim s\prime\)
\(Q(s,a)\)函数是确定动作a后的V函数
V函数是所有动作a的Q函数的期望 \[ V^\pi(s) = E_{a \sim \pi(a \mid s)}[Q^\pi(s, a)] \] ## 值函数的作用
值函数用来对策略\(\pi(a\mid s)\)进行评估。
如果在状态s,有一个动作a使得\(Q^\pi(s, a) > V^\pi(s)\)
- s状态,执行动作a 比 s状态 所有动作的期望,都要好。状态a高于所有状态的平均值
- 说明执行动作a比当前策略\(\pi(a \mid s)\)好
- 调整参数使\(\pi(a \mid s)\)的概率增加
贝尔曼和贝尔曼最优方程
- \(V(s)\)函数和\(Q(s,a)\)函数
- 贝尔曼方程(选择所有可能的均值)
- 贝尔曼最优方程(直接选择最大值)
V函数与Q函数
V函数:以s为初始状态,执行策略\(\pi\)得到的期望回报(所有轨迹回报的均值) \[
V^\pi(s) = E_{\tau \sim p(\tau)} [\sum_{t=0}^{T-1}r_{t+1} \mid \tau_{s_0} = s]
\] Q函数:以s为初始状态,执行动作a,执行策略\(\pi\)得到的期望回报 \[
Q^\pi(s, a) = E_{s\prime \sim p(s\prime \mid s, a)} [r(s, a, s\prime) + \gamma V^\pi(s\prime)]
\] 利用V函数去计算Q函数 \[
Q^\pi(s, a) = E_{s\prime \sim p(s\prime \mid s, a)} [r(s, a, s\prime) + \gamma V^\pi(s\prime)]
\]
贝尔曼方程
\(V(s)\)的贝尔曼方程,选择所有a的期望回报, 也是Q函数的均值,\(V(s)=E_a[Q(s, a)]\) \[ V^\pi(s) = E_{a \sim \pi(a \mid s)}E_{s\prime \sim p(s\prime \mid s, a)}[ r(s, a, s\prime) + \gamma V^\pi(s\prime)] \]
\[ V^\pi(s) = E_{a \sim \pi(a \mid s)}[Q^\pi(s, a)] \]
\(Q(s,a)\)函数的贝尔曼方程 \[ Q^\pi(s, a) = E_{s\prime \sim p(s\prime \mid s, a)} [r(s, a, s\prime) + \gamma E_{a\prime \sim \pi(a\prime \mid s\prime)}[Q^\pi(s\prime, a\prime)]] \]
贝尔曼最优方程
\(V(s)\)函数的贝尔曼最优方程,实际上是直接选择所有a中的最大回报 : \[ V^*(s) = \max_\limits{a} E_{s^\prime \sim p(s^\prime \mid s, a)}[r(s, a, s^\prime) + \gamma V^*(s^\prime)] \] \(Q(s,a)\)函数的贝尔曼最优方程 \[ Q^*(s, a) = E_{s^\prime \sim p(s^\prime \mid s, a)}[r(s, a, s^\prime) + \gamma \max_\limits{a\prime}Q^*(s^\prime, a^\prime)] \]
深度强化学习
有些任务的状态和动作非常多,并且是连续的。普通方法很难去计算。
可以使用更复杂的函数(深度神经网络)使智能体来感知更复杂的环境状态,建立更复杂的策略。
深度强化学习
强化学习-- 定义问题和优化目标深度学习-- 解决状态表示、策略表示等问题
