一切都应该尽可能简单,但不能过于简单。
本文主要是总结:注意力机制、注意力机制的变体、论文中常见的注意力
注意力机制系统介绍
问题背景
计算能力不足
神经网络有很强的能力。但是对于复杂任务,需要大量的输入信息和复杂的计算流程。计算机的计算能力是神经网络的一个瓶颈。
减少计算复杂度
常见的:局部连接、权值共享、汇聚操作。
但仍然需要:尽量少增加模型复杂度(参数),来提高模型的表达能力。
简单文本分类可以使用单向量表达文本
只需要一些关键信息即可,所以一个向量足以表达一篇文章,可以用来分类。
阅读理解需要所有的语义
文章比较长时,一个RNN很难反应出文章的所有语义信息。
对于阅读理解任务来说,编码时并不知道会遇到什么问题。这些问题可能会涉及到文章的所有信息点,如果丢失任意一个信息就可能导致无法正确回答问题。
网络容量与参数成正比
神经网络中可以存储的信息称为网络容量。 存储的多,参数也就越多,网络也就越复杂。 LSTM就是一个存储和计算单元。
注意力和记忆力解决信息过载问题
输入的信息太多(信息过载问题),但不能同时处理这些信息。只能选择重要的信息进行计算,同时用额外空间进行信息存储。
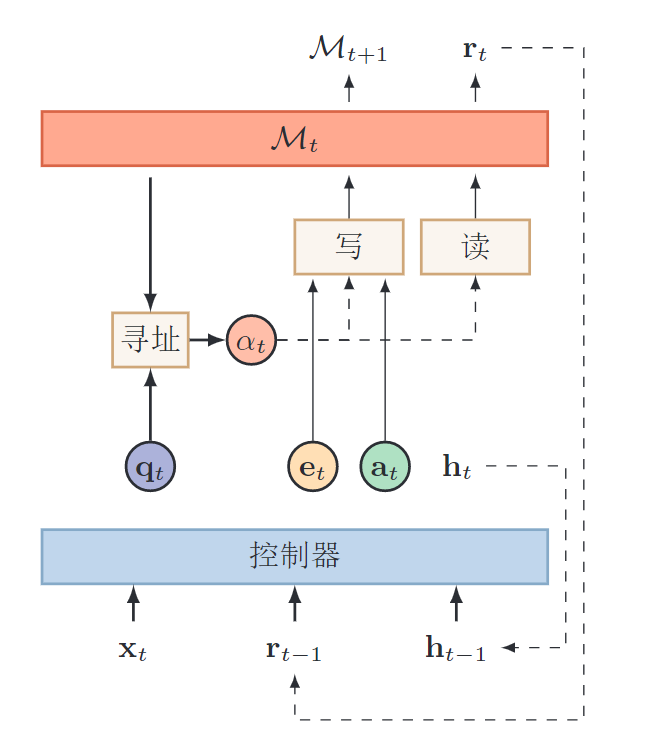
信息选择:聚焦式自上而下地选择重要信息,过滤掉无关的信息。注意力机制外部记忆: 优化神经网络的记忆结构,使用额外的外部记忆,来提高网络的存储信息的容量。 记忆力机制
比如,一篇文章,一个问题。答案只与几个句子相关。所以只需把相关的片段挑选出来交给后续的神经网络来处理,而不需要把所有的文章内容都给到神经网络。
注意力
注意力机制Attention Mechanism 是解决信息过载的一种资源分配方案,把计算资源分配给更重要的任务。
注意力:人脑可以有意或无意地从大量的输入信息中,选择小部分有用信息来重点处理,并忽略其它信息
聚焦式注意力
自上而下有意识的注意力。有预定目的、依赖任务、主动有意识的聚焦于某一对象的注意力。
一般注意力值聚焦式注意力。聚焦式注意力会根据环境、情景或任务的不同而选择不同的信息。
显著性注意力
自下而上无意识的注意力。由外界刺激驱动的注意力,无需主动干预,也和任务无关。如Max Pooling和Gating。
鸡尾酒效应
鸡尾酒效应可以理解这两种注意力。 在吵闹的酒会上
- 噪音很多,依然可以听到朋友谈话的内容
- 没有关注背景声音,但是突然有人叫自己(重要信息),依然会马上注意到
普通注意力机制
把目前的最大汇聚Max Pooling和门控Gating 近似地看做自下而上的基于显著性的注意力机制。
为了节省资源,选择重要的信息给到后续的神经网络进行计算,而不需要把所有的内容都给到后面的神经网络。
输入N个信息
\(X_{1:N} = [\mathbf{x}_1, \cdots, \mathbf{x}_N]\), 问题\(\mathbf{q}\)。 要从\(X\)中选择一些和任务相关的信息输入给神经网络。
计算注意力分布
\(\alpha_i\) : 选择第\(i\)个信息的概率,也称为注意力分布 ,\(z\)表示被选择信息的索引位置 \[
\alpha_i = p(z = i \mid X, \mathbf{q}) =
\rm{softmax}\left(s(\mathbf{x}_i, \mathbf{q})\right)
= \frac{\exp\left(s(\mathbf{x}_i, \mathbf{q})\right)}{\sum_{j=1}^N \exp\left(s(\mathbf{x}_j, \mathbf{q})\right)}
\]
NMT里面三种score打分函数 : \[
\color{blue}{\rm{score}(h_t, \bar h_s)} =
\begin{cases}
h_t^T \bar h_s & \text{dot} \\
h_t^T W_a \bar h_s & \text{general} \\
v_a^T \tanh (W_a [h_t; \bar h_s]) & \text{concat} \\
\end{cases}
\] 加性模型 \[
s(\mathbf{x}_i, \mathbf{q}) = v^T\rm{tanh} (W\mathbf{x}_i + U\mathbf{q})
\] 点击模型 \[
s(\mathbf{x}_i, \mathbf{q}) = \mathbf{x}_i^T \mathbf{q}
\] 计算注意力
Soft Attention 是对所有的信息进行加权求和。Hard Attention是选择最大信息的那一个。
使用软性注意力选择机制,对输入信息编码为,实际上也是一个期望。 \[
\rm{attn} (X, \mathbf q) = \sum_{i=1}^N \alpha_i \mathbf x_i = E_{z\sim p(z\mid X, \mathbf{q})} [X]
\] 
应用与优点
传统机器翻译Encoder-Decoder的缺点:
- 编码向量容量瓶颈问题:所有信息都需要保存在编码向量中
- 长距离依赖问题:长距离信息传递时,信息会丢失
注意力机制直接从源语言信息中选择相关的信息作为辅助,有下面几个好处:
- 解码过程中每一步都直接访问源语言所有位置上的信息。无需让所有信息都通过编码向量进行传递。
- 缩短了信息的传递距离。源语言的信息可以直接传递到解码过程中的每一步
图像描述生成
注意力机制变体
多头注意力
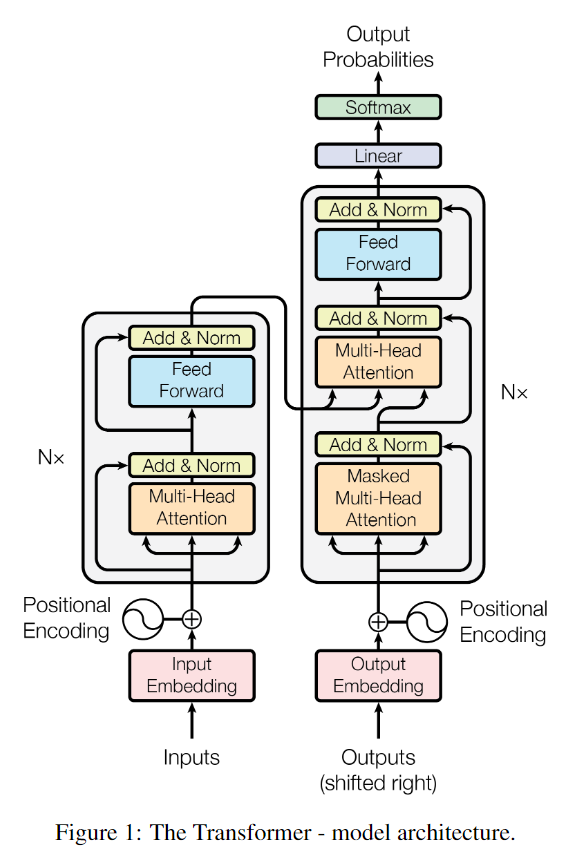
Multi-head Attention利用多个查询\(\mathbf{q}_{1:M}={\mathbf{q}_1, \cdots, \mathbf{q}_M}\)来并行地从输入信息中选取多个信息。每个注意力关注输入信息的不同部分。比如Attention Is All You Need。

硬性注意力
硬性注意力是只关注到一个位置上。
- 选取最高概率的输入信息
- 在注意力分布上随机采样
缺点:loss与注意力分布之间的函数关系不可导,无法使用反向传播训练。一般使用软性注意力。
需要:硬性注意力需要强化学习来进行训练。
键值对注意力
输入信息:键值对(Key, Value)。 Key用来计算注意力分布\(\alpha_i\),值用来生成选择的信息。 \[
\rm{attn} (\mathbf{(K, V)}, \mathbf q) = \sum_{i=1}^N \alpha_i \mathbf v_i
= \sum_{i=1}^N\frac{\exp\left(s(\mathbf{k}_i, \mathbf{q})\right)}{\sum_{j=1}^N \exp\left(s(\mathbf{k}_j, \mathbf{q})\right)} \mathbf v_i
\] 
结构化注意力
普通注意力是在输入信息上的一个多项分布,是一个扁平结构。
如果输入信息,本身就有层次化的结构,词、句子、段落、篇章等不同粒度的层次。这时用层次化的注意力来进行更好的信息选择。
也可以使用一种图模型,来构建更加复杂的结构化注意力分布。
指针网络
前面的都是计算注意力对信息进行筛选:计算注意力分布,利用分布对信息进行加权平均。
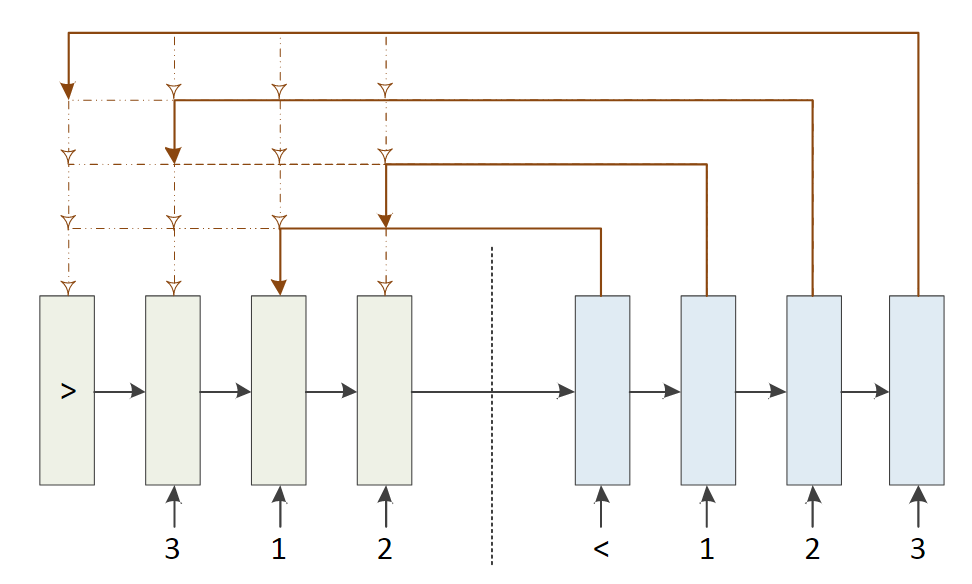
指针网络pointer network是一种序列到序列的模型,用来指出相关信息的位置。也就是只做第一步。
输入: \(X_{1:n} = [\mathbf{x}_1, \cdots, \mathbf{x}_n]\)
输出:\(c_{1:m} = c_1, c_2, \cdots, c_m, \; c_i \in [1,n]\), 输出是序列的下标。如输入123,输出312
条件概率 \[ p(c_{1:m} \mid \mathbf x_{1:n}) = \prod_{i=1}^m p(c_i \mid c_{1:i-1}, \mathbf x_{1:n}) \approx \prod_{i=1}^m p(c_i \mid \mathbf x_{c_1}, \cdots, \mathbf x_{c_{i-1}}\mathbf x_{1:n}) \]
\[ p(c_i \mid c_{1:i-1}, \mathbf x_{1:n}) = \rm{softmax}(s_{i,j}) \]
第i步时,每个输入向量的得分(未归一化的注意力分布): \[ s_{i,j} = v^T\rm{tanh} (W\mathbf{x}_j + U\mathbf{e}_i) \] 其中向量\(\mathbf e_i\)是第i个时刻,RNN对\(\mathbf x_{c_1}, \cdots, \mathbf x_{c_{i-1}}\mathbf x_{1:n}\) 的编码。
各种注意力计算模型
注意力的本质
有\(k\)个\(d\)维的特征向量\(\mathbf h_i \;(i \in [1,k])\),想要整合这k个特征向量的信息。得到一个向量\(\mathbf h^*\),一般也是d维。
- 简单粗暴:对k个向量求平均。当然不合理啦。
- 加权平均:\(\mathbf h^* = \sum_{i=1}^k \alpha_i \mathbf h_i\) 。
合理
所以最重要的就是合理地求出\(\alpha_i\),根据所关心的对象\(\mathbf q\)(可能是自身)去计算注意力分布
- 针对每个\(\mathbf h_i\), 计算出一个得分,\(s_i\)。 \(h_i\)与\(q\)越相关,得分越高。
- \(\alpha_i = \rm{softmax}(s_i)\)
\[ s_i = \rm{score}(\mathbf h_i, \mathbf q) \]
打分函数的计算:(NMT里面三种score打分函数 )
Local-based Attention,没有外部的关注对象,自己关注自己。General Attention, 有外部的关注对象,直接乘积,全连接层。Concatenation-based Attention, 有关注的对象,先concat或相加再过连接层。
Local-based
没有外部的信息,每个向量的得分与自己相关,与外部无关。
比如:Where is the football? ,where和football在句子中起总结性作用。Attention只与句子中的每个词有关。
一个句子,有多个词,多个向量。通过自己计算注意力分布,再对这些词的注意力进行加权求和,则可以得到这个句子的最终表达。 \[ s_i = f(\mathbf h_i) = \rm{a}(W^T \mathbf h_i + b) \]
\[ \mathbf h^* = \sum_{i=1}^n s_i \cdot \mathbf h_i \]
a是激活函数。 sigmoid, tanh, relu, maxout, y=x(无激活函数)。
1 一个得分简单求法
A Context-Aware Attention Network For Interactive Question Answering
利用自己计算注意力分布 \[ \gamma_j = \rm{softmax} (\mathbf v^T \mathbf g_j^q) \] 利用新的注意力分布去计算最终的attention向量 \[ \mathbf u = W_{ch} \sum_{j=1}^N \gamma_j \mathbf g_j^q + \mathbf b_c ^q \] 2 两个得分合并为一个得分
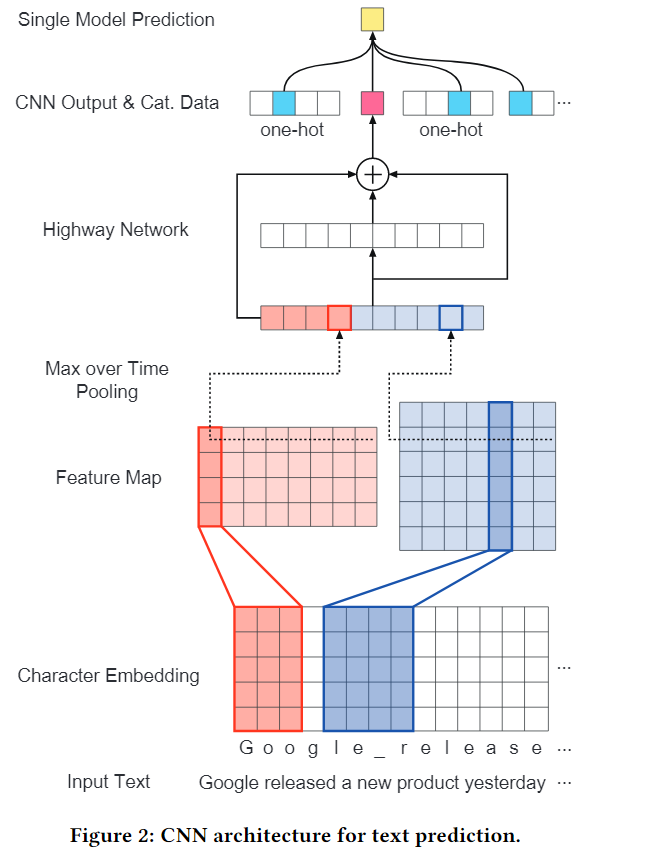
Dynamic Attention Deep Model for Article Recommendation by Learning Human Editors’ Demonstration
计算两个得分 \[ \lambda _{m_t}^M = w_{m_t}^M \cdot \mathbf o + b_{m_t}^M , \quad \lambda_t ^T = w_t^T \cdot \mathbf o + b_t^T \] 权值合并,求注意力分布: \[ p_t = \rm{softmax} (\alpha \lambda _{m_t}^M + (1-\alpha) \lambda_t ^T) \] 3 论文图片
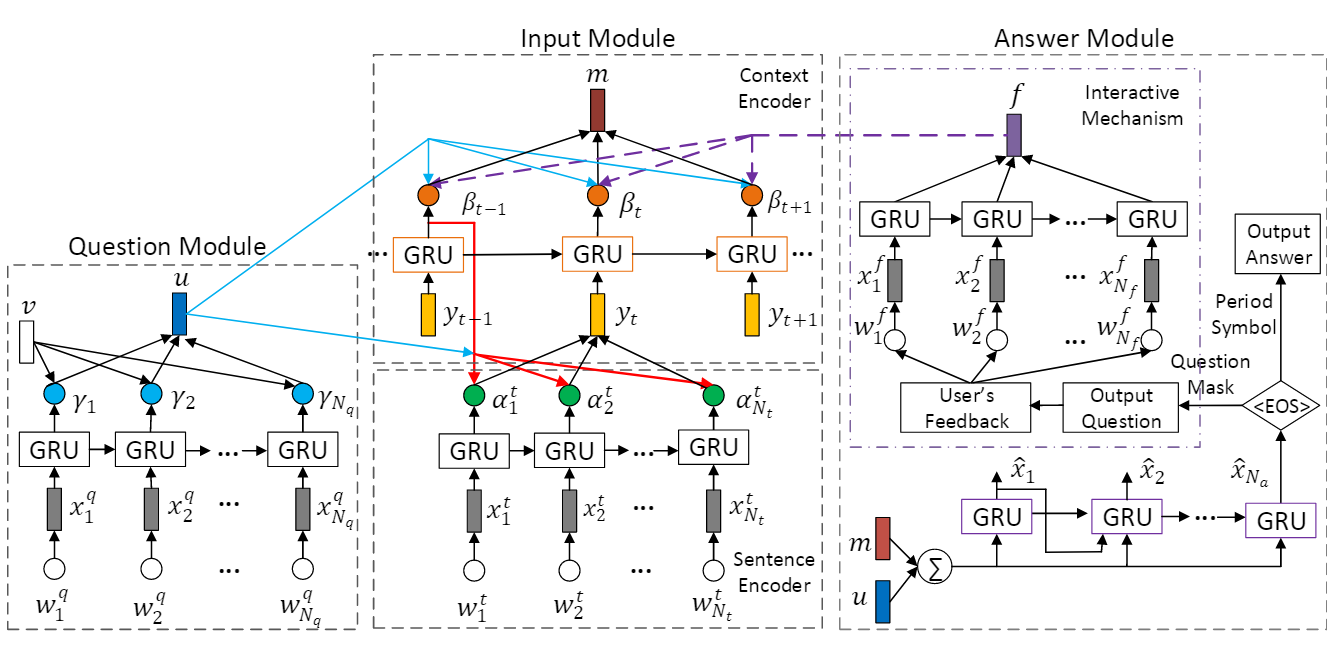
CAN for QA

Dynamic Attention


General Attention
有外部的信息,\(\mathbf h_i\) 与 \(\mathbf q\)进行乘积得分。 机器翻译的应用 \[ \rm{score}(\mathbf h_i, \mathbf q) = \mathbf h_i^T W\mathbf q \]
Concatenation-based
要关注的外部对象是\(\mathbf h_t\), 可以随时间变化,也可以一直不变(question)。 \[ s_i = f(\mathbf h_i, \mathbf h_t) = \mathbf v^T \rm a(W_1 \mathbf h_i + W_2 \mathbf h_t + b) \] 1 多个元素组成Attention
Item-Level Attention。可以看到需要加什么Attention,直接向公式里面一加就可以了。 \[ a(i, l) = w_1^T \phi(W_{1u} \mathbf u_i + W_{1v} \mathbf v_l + W_{1p} \mathbf p_l + W_{1x} \mathbf {\bar x}_l + \mathbf b_1) + \mathbf c_1 \]
\[ \alpha(i, l) = \frac {\exp (a(i, l))} {\sum_{n \in R(i)} \exp (a(i, n))} \]
多层Attention
有\(m\)个句子,每个句子有\(k\)个词语。
Word-level Attention
每个句子,有k个词语,每个词语一个词向量,使用Local-based Attention , 可以得到这个句子的向量表达\(\mathbf s_i\)。
Sentence-level Attention
有\(m\)个句子,每个句子是一个句子向量\(\mathbf s_i\)。 可以再次Attention,得到文档的向量表达\(\mathbf d\), 也可以得到每个句子的权值\(\alpha_i\)。
得到这些信息之后,再具体问题具体分析。
1. 文章摘要生成
输入一篇文档,输出它的摘要。
- 第一层:
Local-based Attention, 生成每个句子的vector - 第二层:当前句子作为中心,2n+1个句子。输入RNN(不明白)。将中心句子作为attention,来编码上下文。通过上下文对中心句子进行打分。作为该句子对整个文本的重要性
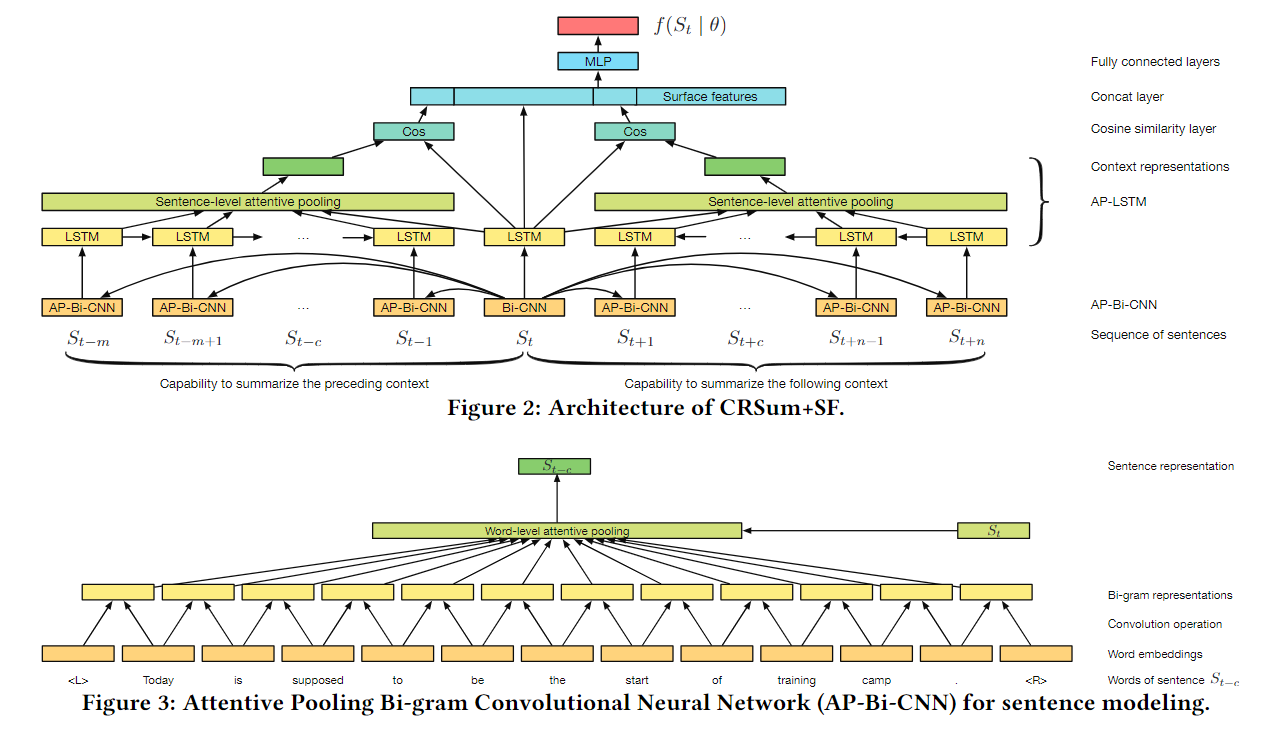
CAN的实时问答
A Context-Aware Attention Network For Interactive Question Answering
第一层Attention
对句子过GRU,每一时刻的output作为词的编码。再使用Local-Attention对这些词,得到问句的表达\(\mathbf u\)。
第二层Attention
由于上下文有多个句子。
首先,对一个句子进行过GRU,得到每一时刻单词的语义信息\(\alpha^t\), 然后利用Concat-Attention对这些单词计算,得到这句话的语义信息\(\mathbf y_t\)。
再把当前句子的语义信息给到句子的GRU
第三次Attention
经过GRU,得到每个句子的表达\(\mathbf s_t\)。 再使用Concat-Attention来得到每个句子的注意力分配\(\mathbf \beta_t\), 然后加权求和得到 整个Context的表达\(\mathbf m\)。
输出
结合\(\mathbf {m, u}\)通过GRU去生成答案
Period Symbol:是正确答案,直接输出Question Mask: 输出是一个问题,要继续问用户相应的信息
用户重新给了反馈之后,对所有词汇信息使用simple attention mechanism, 即平均加权,所有的贡献都是一样的。得到反馈的向量表达\(\mathbf f\)。
使用新的反馈向量和原始的问句向量,结合,重新生成新的context的语义表达\(\mathbf m\)。 最终得到新的\(\mathbf {m, u}\) 去重新回答。 \[ \mathbf r = \tanh (W_{rf}f + \mathbf b_r^{(f)}) \]
\[ \beta_t = \rm{softmax}(\mathbf u^T \mathbf s_t + \mathbf r^T \mathbf s_t) \]