先放四张图,分别是DCN的Encoder、Decoder,DCN+的Encoder和Objective。后面再详细总结
Dynamic Coattention Networks For Question Answering
DCN+: Mixed Objective and Deep Residual Coattention for Question Answering
DCN
Coattention Encoder
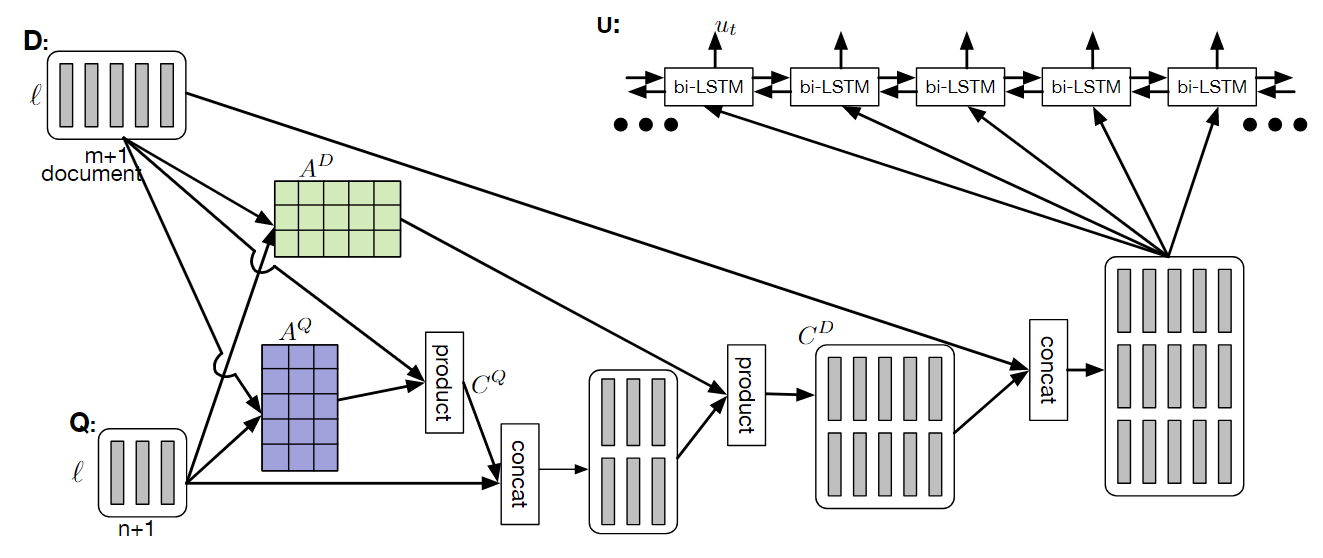
Dynamic Pointing Decoder
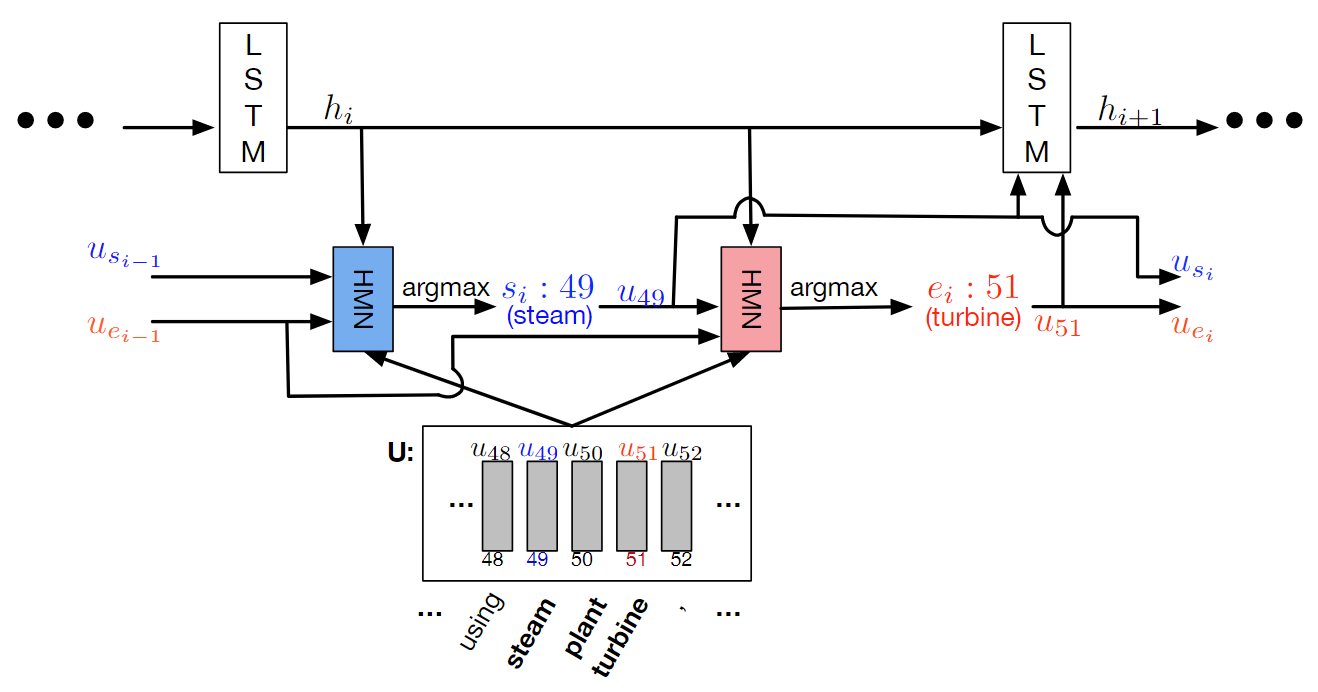
HMN
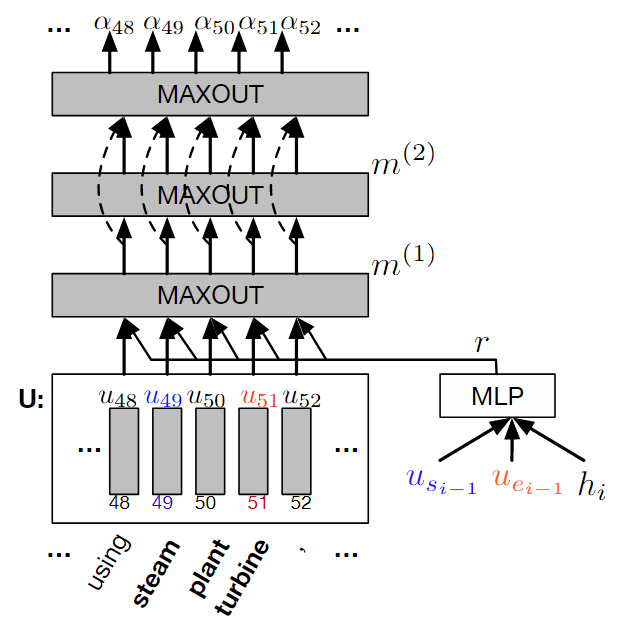
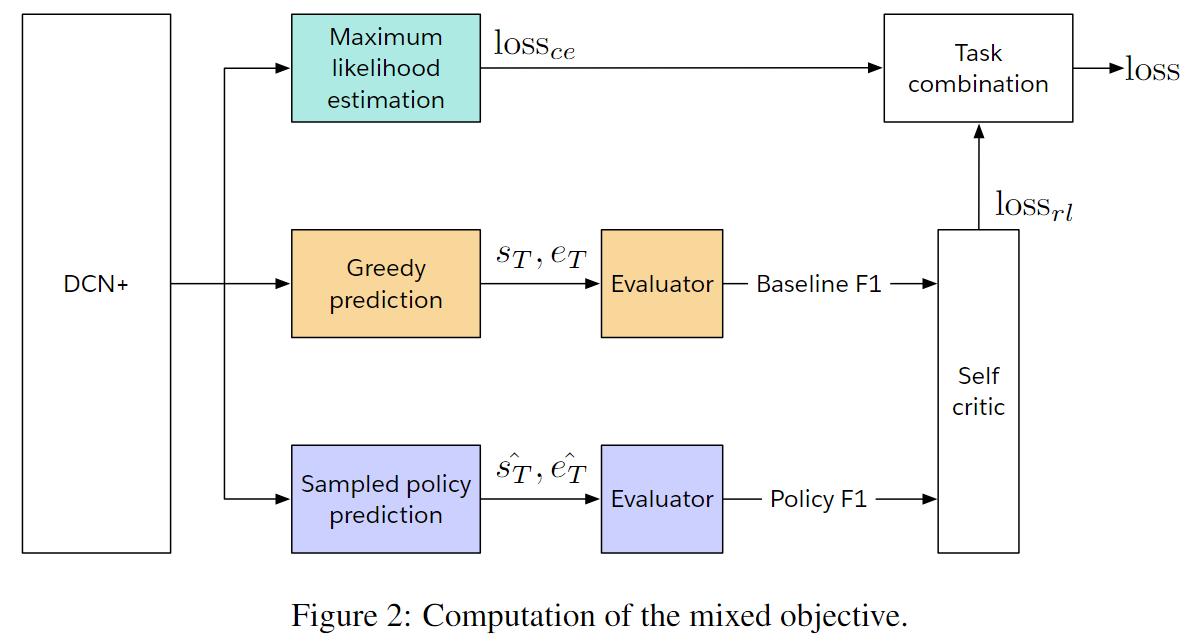
DCN+
DCN的问题
loss没有判断真正的意义
DCN使用传统交叉熵去优化optimization,只考虑答案字符串的匹配程度。但是实际上人的评判evaluation却是看回答的意义。如果只考虑span,则有下面两个问题:
- 精确答案:没影响
- 但是对正确答案周围重叠的单词,却可能认为是错误的。
句子:Some believe that the Golden State Warriors team of 2017 is one of the greatest teams in NBA history
问题:which team is considered to be one of the greatest teams in NBA history
正确答案:the Golden State Warriors team of 2017
其实Warriors也是正确答案, 但是传统交叉熵却认为它还不如history。
DCN没有建立起Optimization和 evaluation的联系。 这也是Word Overlap。
单层coattention表达力不强
DCN+的优化点
Mixed Loss
交叉熵+自我批评学习(强化学习)。Word真正意义相似才会给一个好的reward。
- 强化学习会鼓励意义相近的词语,而dis不相近的词语
- 交叉熵让强化学习朝着正确的轨迹发展
Deep Residual Coattention Encoder
多层表达能力更强,详细看下面的优点。
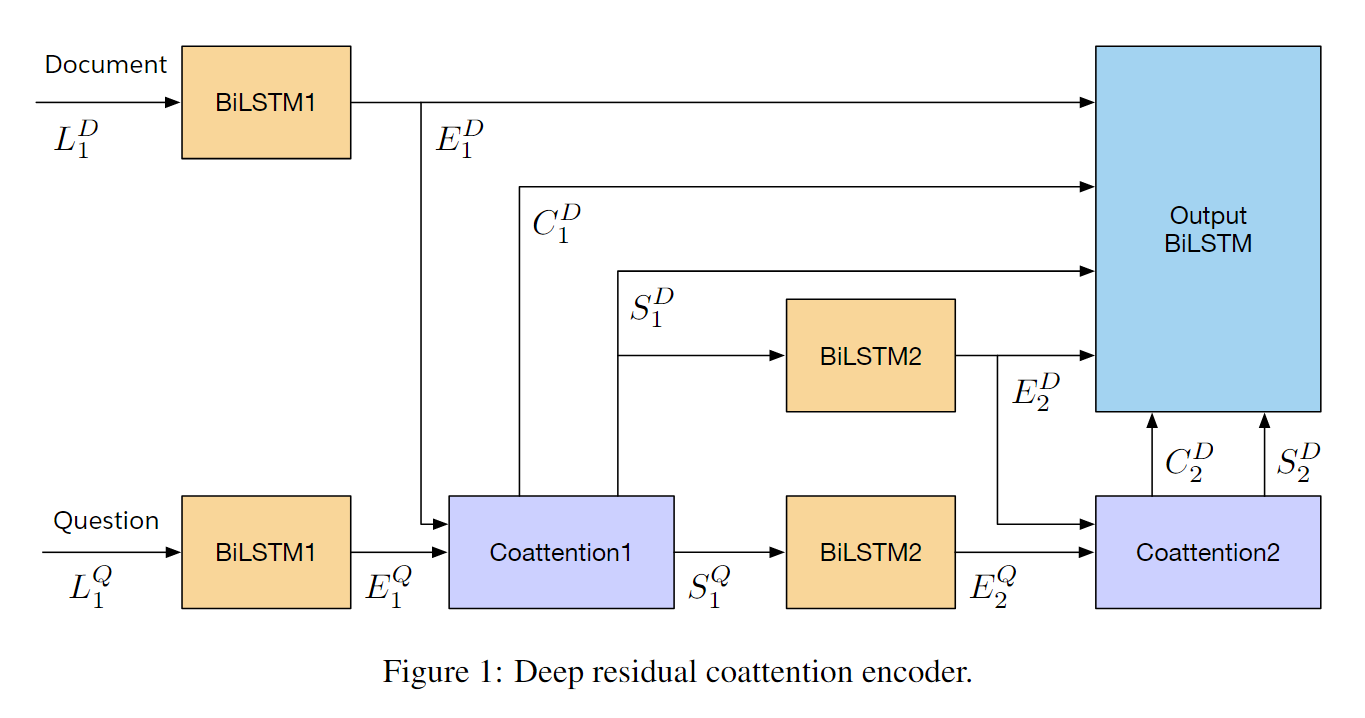
Deep Residual Encoder
优点
两个别人得出的重要结论:
stacked self-attention可以加速信号传递- 减少信号传递路径,可以增加长依赖
比DCN的两个优化点:
coattention with self-attention和多层coattention。可以对输入有richer representations- 对每层的
coattention outputs进行残差连接。缩短了信息传递路径。
Coattention深层理解
当时理解了很久都不懂,后来一个下午,一直看,结合机器翻译实现和实际例子矩阵计算,终于理解了Attention、Coattention。
参考了我的下面三篇笔记。
单个Coattention层计算
经过双向RNN后,得到两个语义编码:文档\(E_0^D \in \mathbb R^{m\times e}\), 问题编码\(E^Q_0 \in \mathbb R ^{n \times h}\) 。 \[ E_1^D = \rm{biGRU_1}(E_0^D) \quad\in \mathbb R^{m \times h} \]
\[ E_1^Q = \tanh(\rm{W \; \rm{biGRU_1(Q_E)+b)}} \quad \in \mathbb R^{n \times h} \]
计算关联得分矩阵A \[
A = E_1^D (E_1^Q)^T \in \mathbb R^{m \times n}
\]
\[ \begin{bmatrix} 0 & 0 \\ 2 & 3 \\ 0 & 2 \\ 1 & 1 \\ 3 & 3 \\ \end{bmatrix}_{5 \times 2} \cdot \begin{bmatrix} 1& 3 \\ 1 & 1 \\ 1& 3 \\ \end{bmatrix}_{3 \times 2}^T = \begin{bmatrix} 0& 0 &0 \\ 11& 5 &11 \\ 6& 2 &6 \\ 4& 2 &4 \\ 12& 6 &12 \\ \end{bmatrix}_{5\times 3} \]
做行Softmax,得到Q对D的权值分配概率\(A^Q\), attention_weights
- 每一行是一个文档单词w
- 元素值是所有问句单词对当前文档单词w的注意力分配权值
- 元素值是每个问句单词的权值概率
\[ \begin{bmatrix} 0.3333 & 0.3333 & 0.3333 \\ 0.4994 &0.0012 & 0.4994 \\ 0.4955 &0.0091 &0.4955 \\ 0.4683 &0.0634 &0.4683\\ 0.4994 &0.0012 &0.4994 \\ \end{bmatrix}_{5\times 3} \]
计算D的summary, \(S^D = A^Q \cdot Q\) \[ S^D = A^Q \cdot Q \]
- D所需要的新的语义,参考机器翻译的新语义理解
- \(A^Q\)的每一行去乘以Q的每一列去表达单词w
- 用Q去表达D,每个\(D_w\)都是Q的所有单词对w的线性表达,权值就是\(A^Q\)
- 所以\(S^D\)也是D的
summary, 也称作D需要context
同理,对列做softmax, 得到D对Q的权值分配概率\(A^D\), 得到Q的summary, \(S^Q = A^D \cdot D\)
这时,借鉴alternation-coattention思想 去计算对D的Coattention context\(C^D\) : \[
C^D = S^Q \cdot A^Q
\] 实际上,\(C^D\)与\(S^D\)类似,都是Summary, 都是context。 只是\(C^D\)使用的是新的\(S^Q\), 而不是\(E^Q_1\)。
Coattention Encoder总结

使用两层coattention, 最后再残差连接,经过LSTM输出。
第一层 \[ E_1^D = \rm{biGRU_1}(E_0^D) \quad\in \mathbb R^{m \times h} \\ E_1^Q = \tanh(\rm{W \cdot \rm{biGRU_1(E_0^Q)+b)}} \quad \in \mathbb R^{n \times h} \]
\[ \rm{coattn_1} (E_1^D, E_1^Q) = S_1^D, S_1^Q, C_1^Q \\ \]
第二层 \[ E_2^D = \rm{biGRU_2}(E_1^D) \quad\in \mathbb R^{m \times h} \\ E_2^Q = \tanh (W \cdot \rm{biGRU_2}(E_1^Q) + b) \quad\in \mathbb R^{m \times h} \]
\[ \rm{coattn_2} (E_2^D, E_2^Q) = S_2^D, S_2^Q, C_2^Q \\ \]
残差连接所有的D \[ c = \rm {concat}((E_1^D, E_2^D, S_1^D, S_2^D, C_1^D, C_2^D) \] LSTM编码输出,得到Encoder的输出 \[ U = \rm{biGRU}(c) \quad \in \mathbb R^{m \times 2h} \]
Mixed Objective