cs224n笔记,word2vec总体介绍,包括CBOW和Skip-gram,负采样训练
Word2vec
简介
把词汇变成词向量。
| 类别1 | 类别2 | |
|---|---|---|
| 算法 | CBOW,上下文预测中心词汇 | Skip-gram,中心词汇预测上下文 |
| 训练方法 | 负采样 | 哈夫曼树 |
语言模型
两种句子:
- 正常的句子:
The cat jumped over the puddle。 概率高,有意义。 - 没意义的句子:
stock boil fish is toy。概率低,没意义。
二元模型
一个句子,有\(n\)个单词。每个词出现的概率由上一个词语来决定。则整体句子的概率如下表示: \[ P(w_1, w_2, \cdots, w_n) = \prod_{i=2}^n P(w_i \mid w_{i-1}) \] 缺点
- 只考虑单词相邻传递概率,而忽略句子整体的可能性。
- context size=1,只学了相邻单词对的概率
- 会计算整个大数据集的全局信息
CBOW
给上下文The cat _ over the puddle,预测jump 。对于每个单词,学习两个向量:
- \(v\) :
输入向量,(上下文单词) - \(u\):
输出向量, (中心单词)
符号说明
- \(V\) :词汇表,后面用\(V\)代替词汇表单词个数
- \(w_i\) :词汇表中第\(i\)个单词
- \(d\) :向量的维数
- \(\mathcal V_{d \times |V|}\):输入矩阵,也可以用\(W\)来表达
- \(v_i\) :\(\mathcal{V}\)的第\(i\)列,\(w_i\)的输入向量表达
- \(\mathcal {U}_{|V| \times d}\) :输出矩阵,可以用\(W ^ \prime\)来表达
- \(u_i\) :\(\mathcal U\)的第i行, \(w_i\)的输出向量表达
输入与输出
- \(x^{(c)}\), 输入\(2m\)个上下文单词,上下文词汇的one-hot向量
- \(y_c\): 真实标签
- \(\hat y^{(c)}\), 输出一个中心单词,中心词汇的one-hot向量
步骤
1 上下文单词onehot向量
one-hot向量的表达:\((x^{(c-m)}, \cdots, x^{(c-1)}, x^{(c+1)}, x^{(c+m)} \in \mathbb R^V)\)
2 上下文单词向量
\((v_{c-m}, v_{c-m+1}, \cdots. v_{c+m} \in \mathbb{R}^d)\), 其中,\(v_{c-m}=\mathcal V x^{(c-m)}\), 即输入矩阵乘以one-hot向量就找到所在的列
3 平均上下文词向量
\(\hat v = \frac {v_{c-m} + \cdots + v_{c+m}}{2m} \in \mathbb R^d\)
4 输出单词与上下文计算得分向量
\(z = \mathcal U \hat v \in \mathbb R ^V\) 。点积,单词越相似,得分越高
5 得分向量转为概率
$y = (z) R^V $
6 真实预测概率对比
预测的概率向量\(\hat y\)与唯一真实中心单词one-hot向量\(y\),进行交叉熵比较算出loss。
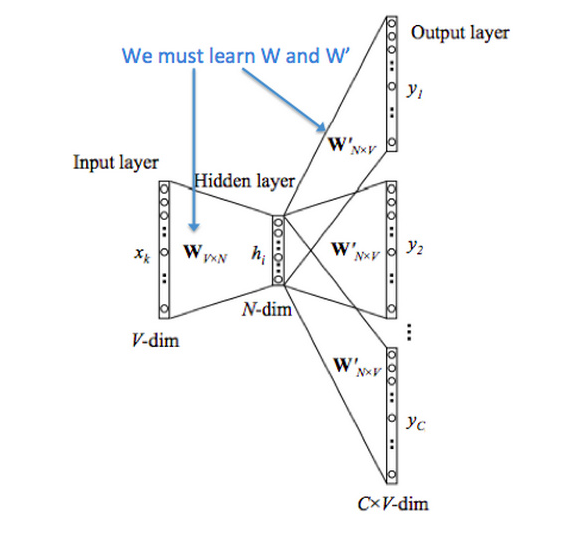
目标函数
使用交叉熵计算loss,损失函数如下: \[
H(\hat y, y) = - \sum_{j=1}^{|V|} y_j \log (\hat y_j)
\] 由于中心单词\(y\)是one-hot编码,只有正确位置才为1,其余均为0,所以只需计算中心单词对应的位置概率的loss即可: \[
H(\hat y, y) = - y_c \log (\hat y_c) = - \log (\hat y_c)
\] 交叉熵很好是因为
- \(-1 \cdot \log (1) = 0\),预测得好
- \(-1 \cdot \log (0.01) = 4.605\), 预测得不好
最终损失函数: \[
\begin{align}
\rm{minimize} \; J
& = - \log P(w_c \mid w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m}) \\
& = - \log P(u_c \mid \hat v) \\
& = - \log \frac {\exp(u_c^T \hat v)}{\sum_{j=1}^{|V|} \exp(u_j^T \hat v)} \\
& = -u_c^T \hat v + \log \sum_{j=1}^{|V|} \exp(u_j^T \hat v)
\end{align}
\] 再使用SGD方法去更新相关的两种向量\(u_c, v_j\) 。
Skip-gram
给中心单词jump,预测上下文The cat _ over the puddle 。
输入中心单词\(x\), 输出上下文单词\(y\) 。与CBOW正好输入输出相反,但同样有两个矩阵\(\mathcal {U, V}\) 。符号说明同CBOW。
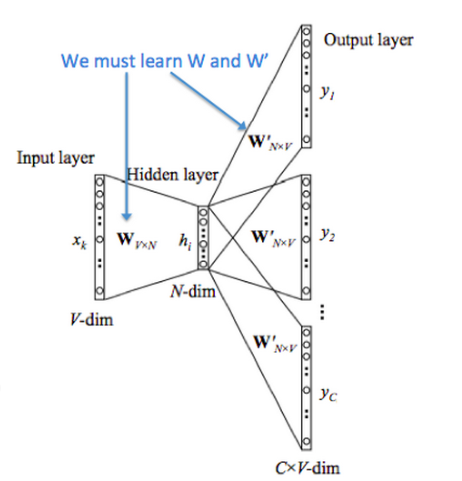
步骤
1 中心单词onehot向量
\(x \in \mathbb {R}^{|V|}\)
2 中心单词词向量
\(v_c = \mathcal V x \in \mathbb R^d\)
3 中心词与其他词的得分向量
\(z = \mathcal U v_c \in \mathbb R ^{|V|}\)
4 得分向量转为概率
概率 \(\hat y = \rm {softmax} (z)\), \(\hat y_{c-m}, \ldots, \hat y_{c+m}\) 是目标上下文单词是中心单词的上下文的预测概率。
5 预测真实概率对比
预测概率\(\hat y\) 与\(2m\) 个真实上下文onehot向量\(y_{c-m}, \ldots, y_{c+m}\)进行交叉熵对比,算出loss
目标函数
与CBOW不同的是,Skip-gram做了一个朴素贝叶斯条件假设,所有的输出上下文单词都是独立的。 \[ \begin {align} \rm{minimize} \; J & = - \log P(w_{c-m}, \ldots, w_{c-1}, w_{c+1}, \ldots, w_{c+m} \mid w_c) \\ & = - \log \prod_{j=0, j \neq m}^{2m} P(w_{c-m+j} \mid w_c) \\ & = -\log \prod_{j=0, j \neq m}^{2m} \frac {\exp (u_{c-m+j}^T \cdot v_c)} {\sum_{k=1}^{|V|} \exp (u_k^T \cdot v_c)} \\ & = - \sum_{j=0, j \neq m}^{2m} \left ( \log \exp (u_{c-m+j}^T \cdot v_c) - \log \sum_{k=1}^{|V|} \exp (u_k^T \cdot v_c) \right) \\ & = - \sum_{j=0, j \neq m}^{2m} u_{c-m+j}^T v_c + 2m \cdot \log \sum_{k=1}^{|V|} \exp (u_k^T \cdot v_c) \end {align} \] 一样,使用SGD去优化U和V。
损失函数实际上是\(2m\)个交叉熵求和,求出的向量\(\hat y\)与\(2m\)个onehot向量\(y_{c-m+j}\) 计算交叉熵: \[
\begin {align}
J
& = - \sum_{j=0, j \neq m}^{2m} \log P(u_{c-m+j} \mid v_c) \\
& = \sum_{j=0, j \neq m}^{2m} H(\hat y, y_{c-m+j}) \\
\end{align}
\]
负采样训练
每次计算都会算整个\(|V|\)词表,太耗时了。 可以从噪声分布\(P_n(w)\)中进行负采样,来代替整个词表。当然单词采样概率与其词频相关。只需关心:目标函数、梯度、更新规则。
标签函数
对于一对中心词和上下文单词\((w, c)\) ,设标签如下:
- \(P(l = 1 \mid w, c)\), \((w, c)\) 来自于真实语料
- \(P(l = 0 \mid w, c)\) ,\((w, c)\)来自于负样本,即不在语料中
用sigmoid表示标签函数: \[
\begin {align}
& P(l = 1 \mid w, c; \theta) = \sigma (u^T_w v_c) = \frac {1}{ 1 + e^{-u^T_w v_c}} \\
& P(l = 0 \mid w, c; \theta) = 1 - \sigma (u^T_w v_c) = \frac {1}{ 1 + e^{u^T_w v_c} } \\
\end {align}
\]
目标函数
选取合适的\(\theta= \mathcal {U, V}\) ,去增大正样本的概率,减小负样本的概率。设\(D\)为正样本集合,\(\bar D\)为负样本集合。 \[ \begin {align} \theta & = \mathop{\rm{argmax}}_\limits{\theta} \prod_{(w, c) \in D} P(l=1 \mid w, c, \theta) \prod_{(w, c) \in \bar D} P(l=0 \mid w, c, \theta) \\ & = \mathop{\rm{argmax}}_\limits{\theta} \prod_{(w, c) \in D} P(l=1 \mid w, c, \theta) \prod_{(w, c) \in \bar D} (1 - P(l=1 \mid w, c, \theta) )\\ & = \mathop{\rm{argmax}}_\limits{\theta} \sum_{(w, c) \in D} \log P(l=1 \mid w, c, \theta) + \sum_{(w, c) \in \bar D} \log (1 - P(l=1 \mid w, c, \theta) )\\ & = \mathop{\rm{argmax}}_\limits{\theta} \sum_{(w, c) \in D} \log \frac {1}{ 1 + \exp (-u^T_w v_c)}+ \sum_{(w, c) \in \bar D} \log \frac {1}{ 1 + \exp (u^T_w v_c) } \\ & = \mathop{\rm{argmax}}_\limits{\theta} \sum_{(w, c) \in D} \log \sigma(u^T_w v_c) + \sum_{(w, c) \in \bar D} \log \sigma (-u^T_w v_c) \end {align} \] 最大化概率也就是最小化负对数似然 \[ J = - \sum_{(w, c) \in D} \log \sigma(u^T_w v_c) - \sum_{(w, c) \in \bar D} \log \sigma (-u^T_w v_c) \]
负采样集合选择
为中心单词\(w_c\) 从\(P_n(w)\) 采样\(K\)个假的上下文单词。表示为\(\{ \bar u_k \mid k=1\ldots K\}\)
CBOW
给上下文向量\(\hat{v}=\frac {v_{c-m} + \cdots + v_{c+m}}{2m}\) 和真实中心词\(u_c\)
原始loss \[ J = -u_c^T \hat v + \log \sum_{j=1}^{|V|} \exp(u_j^T \hat v) \] 负采样loss \[ J = - \log \sigma (u_c^T \cdot \hat v) - \sum_{k=1}^K \log \sigma (- \bar u_k^T \cdot \hat v) \]
Skip-gram
给中心单词\(v_c\), 和\(2m\)个真实上下文单词\(u_{c-m+j}\)
原始loss \[ J = - \sum_{j=0, j \neq m}^{2m} u_{c-m+j}^T v_c + 2m \cdot \log \sum_{k=1}^{|V|} \exp (u_k^T \cdot v_c) \] 负采样loss \[ J = - \sum_{j=0, j \neq m}^{2m} \log \sigma (u_{c-m+j}^T \cdot v_c) - \sum_{k=1}^K \log \sigma (-\bar u_{k}^T \cdot v_c) \]
