Word2vec之数学模型

Word2vec有两种模型：CBOW和Skip-gram，有两种训练方法：Hierarchical Softmax和Negative Sampling。偏数学公式推导

背景介绍

符号

• \(C\) ：语料Corpus，所有的文本内容，包含重复的词。
• D：词典，D是从C中取出来的，不重复。
• \(w\)：一个词语
• \(m\)：窗口大小，词语\(w\)的前后\(m\)个词语
  
• \(\rm{Context(w)} = C_w\)： 词\(w\)的上下文词汇，取决于\(m\)
• \(v(w)\)： 词典\(D\)中单词\(w\)的词向量
• \(k\)：词向量的长度
  
• \(i_w\)：词语\(w\)在词典\(D\)中的下标
• \(NEG(w)\) ： 词\(w\)的负样本子集

常用公式： \[ \begin {align} & \log (a^n b^m) = \log a^n + \log b^m = n \log a + m \log b \\ \end{align} \]

\[ \log \prod_{i=1}a^i b^{1-i} = \sum_{i=1} \log a^i + \log b^{1-i} = \sum_{i=1} i \cdot \log a + (i-1) \cdot \log b \]

目标函数

n-gram模型。当然，我们使用神经概率语言模型。

\(P(w \mid C_w)\) 表示上下文词汇推出中心单词\(w\)的概率。

对于统计语言模型来说，一般利用最大似然，把目标函数设为： \[ \prod_{w \in C} p(w \mid C_w) \] 一般使用最大对数似然，则目标函数为： \[ L = \sum_{w \in C} \log p(w \mid C_w) \] 其实概率\(P(w \mid C_w)\)是关于\(w\)和\(C_w\)的函数，其中\(\theta\)是待定参数集，就是要求最优 \(\theta^*\)，来确定函数\(F\)： \[ p(w \mid C_w) = F(w, C_w; \; \theta) \] 有了函数\(F\)以后，就能够直接算出所需要的概率。 而F的构造，就是通过神经网络去实现的。

神经概率语言模型

一个二元对\((C_w, w)\)就是一个训练样本。神经网络结构如下，\(W, U\)是权值矩阵，\(p, q\)是对应的偏置。

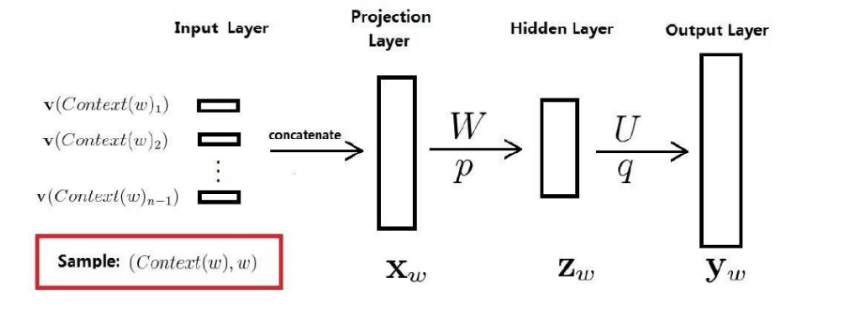
但是一般会减少一层，如下图：（其实是去掉了隐藏层，保留了投影层，是一样的）

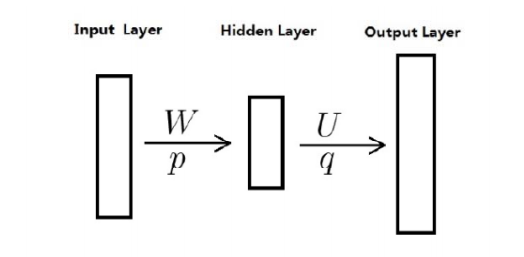
窗口大小是\(m\)，\(\rm{Context}(w)\)包含\(2m\)个词汇，词向量长度是\(k\)。可以做拼接或者求和（下文是）。拼接得到长向量\(2mk\)， 在投影层得到\(\mathbf{x_w}\)，然后给到隐藏层和输出层进行计算。 \[ \mathbf{z}_w = \rm{tanh}(W\mathbf{z}_w + \mathbf{p}) \;\to \;\mathbf{y}_w = U \mathbf{z}_w + \mathbf{q} \] 再对\(\mathbf{y}_w = (y_1, y_2, \cdots, y_K)\) 向量进行softmax即可得到所求得中心词汇的概率： \[ p(w \mid C_w) = \frac{e^{y_{i_w}}}{\sum_{i=1}^K e^{y_i}} \] 优点

• 词语的相似性可以通过词向量来体现
• 自带平滑功能。N-Gram需要自己进行平滑。

词向量的理解

有两种词向量，一种是one-hot representation，另一种是Distributed Representation。one-hot太长了，所以DR中把词映射成为相对短的向量。不再是只有1个1（孤注一掷），而是向量分布于每一维中（风险平摊）。再利用欧式距离就可以算出词向量之间的相似度。

传统可以通过LSA（Latent Semantic Analysis）和LDA（Latent Dirichlet Allocation）来获得词向量，现在也可以用神经网络算法来获得。

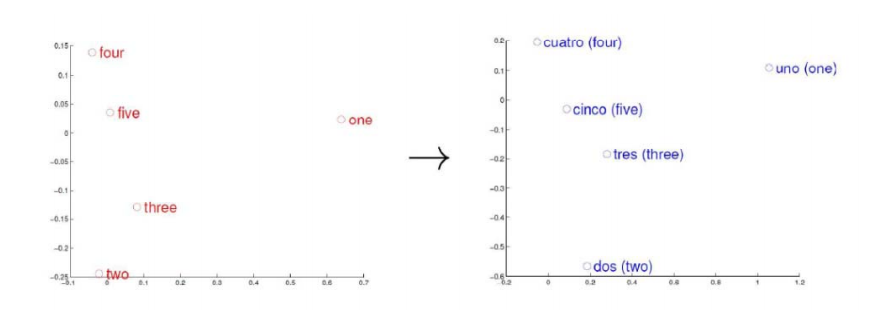
可以把一个词向量空间向另一个词向量空间进行映射，就可以实现翻译。

Hierarchical Softmax

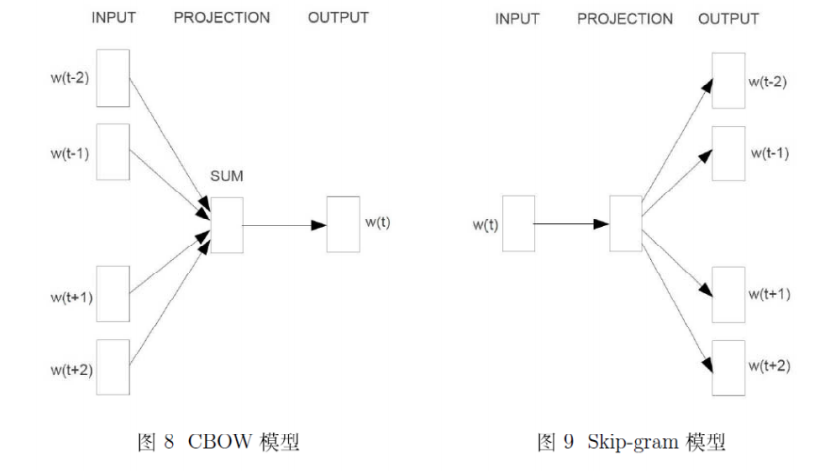
两种模型都是基于下面三层模式（无隐藏层），输入层、投影层和输出层。没有hidden的原因是据说是因为计算太多了。

CBOW和Skip-gram模型：

CBOW模型

一共有\(\left| C \right|\)个单词。CBOW是基于上下文\(context(w) = c_w\)去预测目标单词\(w\)，求条件概率\(p(w \mid c_w)\)，语言模型一般取目标函数为对数似然函数： \[ L = \sum_{w \in C} \log p(w \mid c_w) \] 窗口大小设为\(m\)，则\(c_w\)是\(w\)的前后m个单词。

输入层 是上下文单词的词向量。（初始随机，训练过程中逐渐更新）

投影层 就是对上下文词向量进行求和，向量加法。得到单词\(w\)的所有上下文词\(c_w\)的词向量的和\(\mathbf{x}_w\)，待会儿参数更新的时候再依次更新回来。

输出层 从\(C\)中选择一个词语，实际上是多分类。这里是哈夫曼树层次softmax。

因为词语太多，用softmax太慢了。多分类实际上是多个二分类组成的，比如SVM二叉树分类：

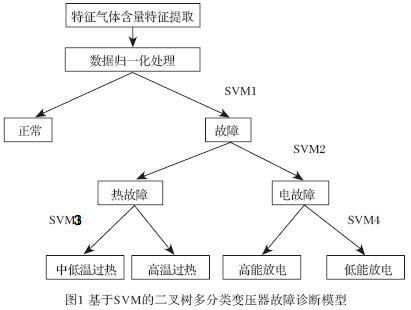
这是一种二叉树结构，应用到word2vec中，被称为Hierarchical Softmax。CBOW完整结构如下：

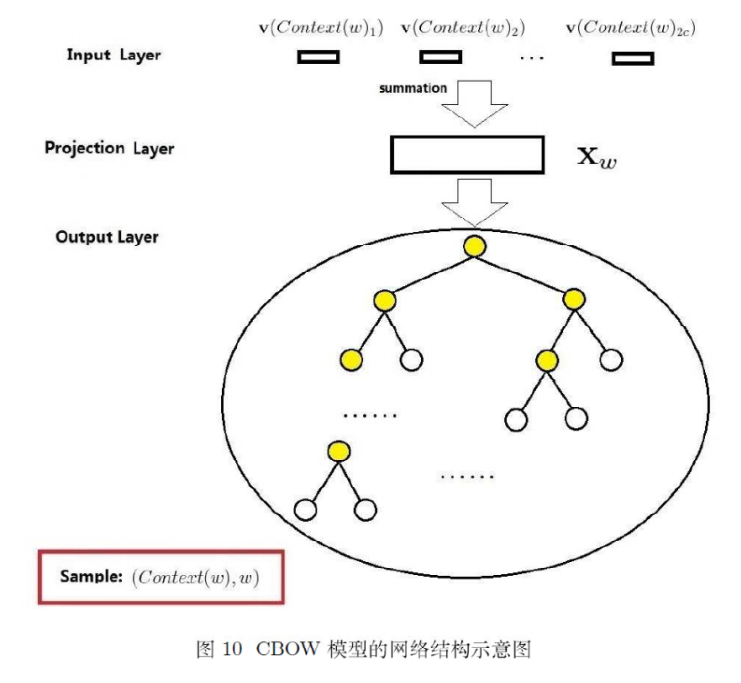
每个叶子节点代表一个词语\(w\)，每个词语被01唯一编码。

哈夫曼编码

哈夫曼树很简单。每次从许多节点中，选择权值最小的两个合并，根节点为合并值；依次循环，直到只剩一棵树。

比如“我 喜欢 看 巴西 足球 世界杯”，这6个词语，出现的次数依次是15, 8, 6, 5, 3, 1。建立得到哈夫曼树，并且得到哈夫曼编码，如下：

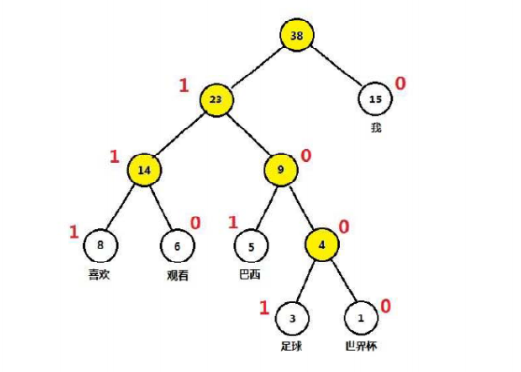
CBOW足球例子

引入一些符号：

• \(p^w\) ：从根节点到达\(w\)叶子节点的路径
• \(l^w\) ： 路径\(p^w\)中节点的个数
• \(p^w_1, \cdots, p^w_{l_w}\) ：依次代表路径中的节点，根节点-中间节点-叶子节点
• \(d^w_2, \cdots, d^w_{l^w} \in \{0, 1\}\)：词\(w\)的哈夫曼编码，由\(l^w-1\)位构成， 根节点无需编码
• \(\theta_1^w, \cdots, \theta^w_{l^w -1}\)：路径中非叶子节点对应的向量， 用于辅助计算。
• 单词\(w\)是足球，对应的所有上下文词汇是\(c_w\)， 上下文词向量的和是\(\mathbf{x}_w\)

看一个例子：

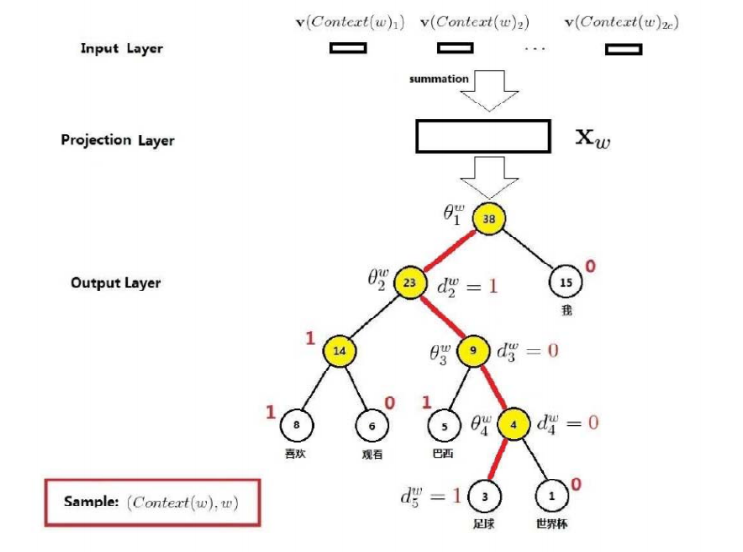
约定编码为1是负类，为0是正类。即左边是负类，右边是正类。

每一个节点就是一个二分类器，是逻辑回归(sigmoid)。其中\(\theta\)是对应的非叶子节点的向量，一个节点被分为正类和负类的概率分别如下： \[ \sigma(\mathbf{x}_w^T \theta) = \frac {1}{ 1 + e^{-\mathbf{x}_w^T \theta}}, \quad 1 - \sigma(\mathbf{x}_w^T \theta) \] 那么从根节点到达足球的概率是： \[ p (足球 \mid c_{足球}) = \prod_{j=2}^5 p(d_j^w \mid \mathbf{x}_w, \theta_{j-1}^w) \]

CBOW总结

目标函数

从根节点到每一个单词\(w\)都存在一条路径\(p^w\)，路径上有\(l^w-1\)个分支节点，每个节点就是一个二分类，每次产生一个概率 \(p(d_j^w \mid \mathbf{x}_w, \theta^w_{j-1})\)， 把这些概率乘起来就得到了\(p(w \mid c_w)\)。

其中每个节点的概率是，与各个节点的参数和传入的上下文向量和\(\mathbf{x}_w\)相关。 \[ p(d_j^w \mid \mathbf{x}_w, \theta^w_{j-1}) = \begin{cases} & \sigma(\mathbf{x}^T_w \theta^w_{j-1}), & d_j^w = 0 \\ & 1 - \sigma(\mathbf{x}^T_w \theta^w_{j-1}), & d_j^w = 1\\ \end{cases} \] 写成指数形式是 \[ p(d_j^w \mid \mathbf{x}_w, \theta^w_{j-1}) = [\sigma(\mathbf{x}^T_w \theta^w_{j-1})]^{1-d_j^w} \cdot [1 - \sigma(\mathbf{x}^T_w \theta^w_{j-1})]^{d_j^w} \] 则上下文推中间单词的概率，即目标函数： \[ p(w \mid c_w) = \prod_{j=2}^{l^w} p(d_j^w \mid \mathbf{x}_w, \theta^w_{j-1}) \] 对数似然函数

对目标函数取对数似然函数是： \[ \begin{align} L & = \sum_{w \in C} \log p(w \mid c_w) = \sum_{w \in C} \log \prod_{j=2}^{l^w} [\sigma(\mathbf{x}^T_w \theta^w_{j-1})]^{1-d_j^w} \cdot[1 - \sigma(\mathbf{x}^T_w \theta^w_{j-1})]^{d_j^w} \\ & = \sum_{w \in C} \sum_{j=2}^{l^w} \left( (1-d_j^w) \cdot \log \sigma(\mathbf{x}^T_w \theta^w_{j-1}) + d_j^w \cdot \log (1 - \sigma(\mathbf{x}^T_w \theta^w_{j-1})) \right) \\ & = \sum_{w \in C} \sum_{j=2}^{l^w} \left( (1-d_j^w) \cdot \log A + d_j^w \cdot \log (1 -A)) \right) \end{align} \] 简写： \[ \begin{align} & L(w, j) = (1-d_j^w) \cdot \log \sigma(\mathbf{x}^T_w \theta^w_{j-1}) + d_j^w \cdot \log (1 - \sigma(\mathbf{x}^T_w \theta^w_{j-1})) \\ & L = \sum_{w,j} L(w, j) \end{align} \] 怎样最大化对数似然函数呢，可以最大化每一项，或者使整体最大化。尽管最大化每一项不一定使整体最大化，但是这里还是使用最大化每一项\(L(w, j)\)。

sigmoid函数的求导： \[ \sigma ^{\prime}(x) = \sigma(x)(1 - \sigma(x)) \] \(L(w, j)\)有两个参数：输入层的\(\mathbf{x}_w\) 和 每个节点的参数向量\(\theta_{j-1}^w\) 。 分别求偏导并且进行更新参数： \[ \begin{align} & \frac{\partial}{\theta_{j-1}^w} L(w, j) = [1 - d_j^w - \sigma(\mathbf{x}^T_w \theta^w_{j-1})] \cdot \mathbf{x}_w \quad \to \quad \theta_{j-1}^w = \theta_{j-1}^w + \alpha \cdot \frac{\partial}{\theta_{j-1}^w} L(w, j) \\ & \frac{\partial}{\mathbf{x}_w} L(w, j) = [1 - d_j^w - \sigma(\mathbf{x}^T_w \theta^w_{j-1})] \cdot \theta_{j-1}^w \quad \to \quad v(\hat w)+= v(\hat w) + \alpha \cdot \sum_{j=2}^{l^w} \frac{\partial}{\mathbf{x}_w} L(w, j), \hat w \in c_w \\ \end{align} \] 注意：\(\mathbf{x}_w\)是所有上下文词向量的和，应该把它的更新平均更新到每个上下文词汇中去。\(\hat w\) 代表\(c_w\)中的一个词汇。

Skip-Gram模型

Skip-gram模型是根据当前词语，预测上下文。网络结构依然是输入层、投影层(其实无用)、输出层。如下：

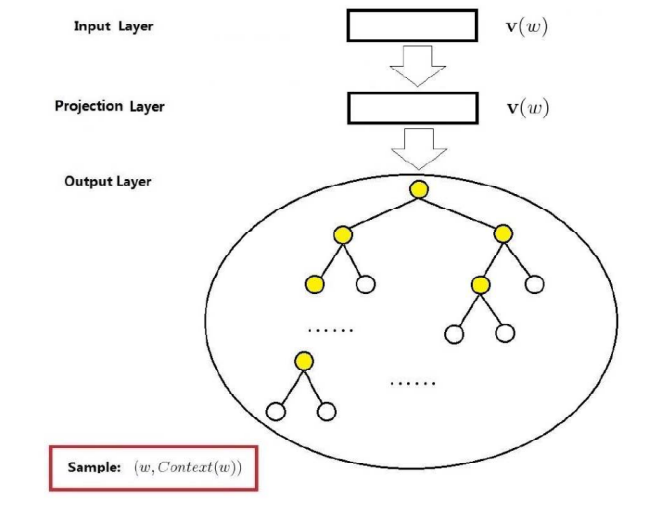
输入一个中心单词的词向量\(v(w)\)，简记为\(v_w\)，输出是一个哈夫曼树。单词\(u\)是\(w\)的上下文单词\(c_w\)中的一个。这是一个词袋模型，每个\(u\)是互相独立的。

目标函数

所以\(c_w\)是\(w\)的上下文词汇的概率是： \[ p(c_w \mid w) = \prod_{u \in c_w} p(u \mid w) \] 与上面同理，\(p(u \mid w)\) 与传入的中心单词向量\(v(w)\)和路径上的各个节点相关： \[ \begin{align} & p(u \mid w) = \prod_{j=2}^{l^w} p(d_j^u \mid v_w,\; \theta^u_{j-1}) \\ & p(d_j^u \mid v_w ,\; \theta^u_{j-1} ) = [\sigma(v_w^T \theta^u_{j-1})]^{1-d_j^u} \cdot [1 - \sigma(v_w^T \theta^u_{j-1})]^{d_j^u} \\ \end{align} \] 下文\(v_w^T \theta^w_{j-1}\)简记为\(v_w \theta_{j-1}^w\)，要记得转置向量相乘就可以了。

对数似然函数 \[ \begin{align} L & = \sum_{w \in C} \log p(c_w \mid w) \\ & = \sum_{w \in C} \log \prod_{u \in c_w} \prod _{j=2}^{l^w} [\sigma(v_w^T \theta^u_{j-1})]^{1-d_j^u} \cdot [1 - \sigma(v_w^T \theta^u_{j-1})]^{d_j^u} \\ & = \sum_{w \in C} \sum_{u \in c_w} \sum_{j=2}^{l^w} \left( (1-d_j^u) \cdot \log \sigma(v_w^T \theta^u_{j-1}) + d_j^u \cdot \log (1 - \sigma(v_w^T \theta^u_{j-1})) \right) \\ \end{align} \] 同样，简写每一项为\(L(w, u, j)\) \[ L(w, u, j) = (1-d_j^u) \cdot \log \sigma(v_w^T \theta^u_{j-1}) + d_j^u \cdot \log (1 - \sigma(v_w^T \theta^u_{j-1})) \] 然后就是，分别对\(v_w\)和\(\theta_{j-1}^u\)求梯度更新即可，同上面的类似。得到下面的更新公式 \[ \begin{align} & \theta_{j-1}^u = \theta_{j-1}^u + \alpha \cdot [1 - d_j^u - \sigma(v_w^t \cdot \theta_{j-1}^u)] \cdot v(w) \\ & v_w = v_w + \alpha \cdot \sum_{u \in c_w} \sum_{j=2}^{l^w} \frac{\partial L(w, u, j)}{\partial v_w} \\ \end{align} \]

Negative Sampling

背景知识介绍

Negative Sampling简称NEG，是Noise Contrastive Estimation(NCE)的一个简化版本，目的是用来提高训练速度和改善所得词向量的质量。

NEG不使用复杂的哈夫曼树，而是使用随机负采样，大幅度提高性能，是Hierarchical Softmax的一个替代。

NCE 细节有点复杂，本质上是利用已知的概率密度函数来估计未知的概率密度函数。简单来说，如果已知概率密度X，未知Y，如果知道X和Y的关系，Y也就求出来了。

在训练的时候，需要给正例和负例。Hierarchical Softmax是把负例放在二叉树的根节点上，而NEG，是随机挑选一些负例。

CBOW

对于一个单词\(w\)，输入上下文\(\rm{Context}(w) = C_w\)，输出单词\(w\)。那么词\(w\)是正样本，其他词都是负样本。 负样本很多，该怎么选择呢？后面再说。

定义\(\rm{Context}(w)\)的负样本子集\(\rm{NEG}(w)\)。对于样本\((C_w, w)\)，\(\mathbf{x}_w\)依然是\(C_w\)的词向量之和。\(\theta_u\)为词\(u\)的一个（辅助）向量，待训练参数。

设集合\(S_w = w \bigcup NEG(w)\) ，对所有的单词\(u \in S_w\)，有标签函数： \[ b^w(u) = \begin{cases} & 1, & u = w \\ & 0, & u \neq w \\ \end{cases} \] 单词\(u\)是\(C_w\) 的中心词的概率是： \[ p(u \mid C_w) = \begin{cases} & \sigma(\mathbf x_w^T \theta^u), & u=w \; \text{正样本} \\ & 1 - \sigma(\mathbf x_w^T \theta^u), & u \neq w \; \text{负样本} \\ \end{cases} \] 简写为： \[ \color{blue} {p(u \mid C_w)} = [ \sigma(\mathbf x_w^T \theta^u)]^{b^w(u)} \cdot [1 - \sigma(\mathbf x_w^T \theta^u)]^{1 - b^w(u)} \] 要最大化目标函数\(g(w) = \sum_{u \in S_w} p(u \mid C_w)\)： \[ \begin{align} \color{blue}{g(w) } & = \prod_{u \in S_w} [ \sigma(\mathbf x_w^T \theta^u)]^{b^w(u)} \cdot [1 - \sigma(\mathbf x_w^T \theta^u)]^{1 - b^w(u)} \\ &= \color{blue} {\sigma(\mathbf x_w^T \theta^u) \prod_{u \in NEG(w)} (1 - \sigma(\mathbf x_w^T \theta^u)) } \\ \end{align} \] 观察\(g(w)\)可知，最大化就是要：增大正样本概率和减小化负样本概率。

每个词都是这样，对于整个语料库的所有词汇，将\(g\)累计得到优化目标，目标函数如下： \[ \begin {align} L & = \log \prod_{w \in C}g(w) = \sum_{w \in C} \log g(w) \\ & = \sum_{w \in C} \log \left( \prod_{u \in S_w} [ \sigma(\mathbf x_w^T \theta^u)]^{b^w(u)} \cdot [1 - \sigma(\mathbf x_w^T \theta^u)]^{1 - b^w(u)} \right) \\ &= \sum_{w \in C} \sum_{u \in S_w} \left[ b^w_u \cdot \sigma(\mathbf x_w^T \theta^u) + (1-b^w_u) \cdot (1 - \sigma(\mathbf x_w^T \theta^u)) \right] \end {align} \] 简写每一步\(L(w, u)\)： \[ L(w, u) = b^w_u \cdot \sigma(\mathbf x_w^T \theta^u) + (1-b^w_u) \cdot (1 - \sigma(\mathbf x_w^T \theta^u)) \] 计算\(L(w, u)\)对\(\theta^u\)和\(\mathbf{x}_w\)的梯度进行更新，得到梯度(对称性)： \[ \frac{\partial L(w, u) }{ \partial \theta^u} = [b^w(u) - \sigma(\mathbf x_w^T \theta^u)] \cdot \mathbf{x}_w, \quad \frac{\partial L(w, u) }{ \partial \mathbf{x}_w} = [b^w(u) - \sigma(\mathbf x_w^T \theta^u)] \cdot \theta^u \] 更新每个单词的训练参数\(\theta^u\) ： \[ \theta^u = \theta^u + \alpha \cdot \frac{\partial L(w, u) }{ \partial \theta^u} \] 对每个单词更新词向量\(v(u)\) ： \[ v(u) = v(u) + \alpha \cdot \sum_{u \in S_w} \frac{\partial L(w, u) }{ \partial \mathbf{x}_w} \]

Skip-gram

H给单词\(w\)，预测上下文向量\(\rm{Context}(w) = C_w\)。 输入样本\((w, C_w)\)。

中心单词是\(w\)，遍历样本中的上下文单词\(w_o \in C_w\)，为每个上下文单词\(w_o\)生成一个包含负采样的集合\(S_o = w \bigcup \rm{NEG}(o)\) 。即\(S_o\)里面只有\(w\)才是\(o\)的中心单词。

下面\(w_o\)简写为\(o\)，要注意实际上是当前中心单词\(w\)的上下文单词。

\(S_o\)中的\(u\)是实际的w就为1，否则为0。标签函数如下：
\[ b^w(u) = \begin{cases} & 1, & u = w \\ & 0, & u \neq w \\ \end{cases} \] \(S_o​\)中的\(u​\)是\(o​\)的中心词的概率是 \[ p(u \mid o) = \begin{cases} & \sigma (v_o^T \theta^u ), & u=w \; \leftrightarrow \; b^w(u) = 1 \\ & 1 - \sigma (v_o^T \theta^u ), &u \neq w \; \leftrightarrow \; b^w(u) = 0 \\ \end{cases} \] 简写为 \[ \color{blue} {p(u \mid o)} = [ \sigma(v_o^T \theta^u)]^{b^w(u)} \cdot [1 - \sigma(v_o^T \theta^u)]^{1 - b^w(u)} \] 对于\(w\)的一个上下文单词\(o\)来说，要最大化这个概率： \[ \prod_{u \in S_o} p(u \mid o ) \] 对于\(w\)的所有上下文单词\(C_w\)来说，要最大化： \[ g(w) = \prod_{o \in C_w} \prod_{u \in S_o} p(u \mid o ) \] 那么，对于整个预料，要最大化： \[ G = \prod_{w \in C} g(w) =\prod_{w \in C} \prod_{o \in C_w} \prod_{u \in S_o} p(u \mid o ) \] 对G取对数，最终的目标函数就是： \[ \begin {align} L & = \log G = \sum_{w \in C} \sum_{o \in C_w} \log \prod_{u \in S_o} p(u \mid o ) \\ &= \sum_{w \in C} \sum_{o \in C_w} \log \prod_{u \in S_o} [ \sigma(v_o^T \theta^u)]^{b^w(u)} \cdot [1 - \sigma(v_o^T \theta^u)]^{1 - b^w(u)} \\ & = \sum_{w \in C} \sum_{o \in C_w} \sum_{u \in S_o} \left ( b^w_u \cdot \sigma(v_o^T \theta^u) + (1 - b^w_u) \cdot (1-\sigma(v_o^T \theta^u)) \right) \end{align} \] 取\(w, o, u\)简写L(w, o, u)： \[ L(w, o, u) = b^w_u \cdot \sigma(v_o^T \theta^u) + (1 - b^w_u) \cdot (1-\sigma(v_o^T \theta^u)) \] 分别对\(\theta^u、v_o\)求梯度 \[ \frac{\partial L(w, o, u) }{ \partial \theta^u} = [b^w_u - \sigma(v_o^T \theta^u)] \cdot v_o, \quad \frac{\partial L(w,o, u) }{ \partial v_o} = [b^w_u - \sigma(v_o^T \theta^u)] \cdot \theta^u \] 更新每个单词的训练参数\(\theta^u\) ： \[ \theta^u = \theta^u + \alpha \cdot \frac{\partial L(w, o,u) }{ \partial \theta^u} \] 对每个单词更新词向量\(v(o)\) ： \[ v(o) = v(o) + \alpha \cdot \sum_{u \in S_o} \frac{\partial L(w, u) }{ \partial v_o} \]