cs224n word2vec 简介和公式推导
Word meaning
词意
词的意思就是idea,如下:
- 词汇本身表达的意义
- 人通过词汇传达的想法
- 在写作、艺术中表达的意思
- signifier - signified(idea or thing) - denotation
传统离散表达
传统使用分类学去建立一个WordNet,其中包含许多上位词is-a和同义词集等。如下:
| 上义词 | 同义词 |
|---|---|
| entity, physical_entity,object, organism, animal | full, good; estimable, good, honorable, respectable |
离散表达的问题:
- 丢失了细微差别,比如同义词:adept, expert, good, practiced, proficient, skillful
- 不能处理新词汇
- 分类太主观
- 需要人力去构建和修改
- 很难去计算词汇相似度
每个单词使用one-hot编码,比如hotel=\([0, 1, 0, 0, 0]\),motel=\([0, 0, 1, 0, 0]\)。 当我搜索settle hotel的时候也应该去匹配包含settle motel的文章。 但是我们的查询hotel向量和文章里面的motel向量却是正交的,算不出相似度。
分布相似表达
通过一个单词的上下文去表达这个单词。
You shall know a word by the company it keeps. --- JR. Firth
例如,下面用周围的单词去表达banking :
government debt problems turning into banking crises as has happened in saying that Europe needs unified banking regulation to replace the hodgepodge
稠密词向量
一个单词的意义应该是由它本身的词向量来决定的。这个词向量可以预测出的上下文单词。
比如lingustics的词向量是\([0.286, 0.792, -0.177, -0.107, 0.109, -0.542, 0.349]\)
词嵌入思想
构建一个模型,根据中心单词\(w_t\),通过自身词向量,去预测出它的上下文单词。 \[ p (context \mid w_t) = \cdots \] 损失函数如下,\(w_{-t}\)表示\(w_t\)的上下文(负号通常表示除了某某之外),如果完美预测,损失函数为0。 \[ J = 1 - p(w_{-t} \mid w_t) \]
Word2Vec
在每个单词和其上下文之间进行预测。
有两种算法:
- Skip-grams(SG): 给目标单词,预测上下文
- Continuous Bag of Words(CBOW):给上下文,预测目标单词
两个稍微高效的训练方法:
- 分层softmax
- 负采样
课上只是Naive softmax。两个模型,两种方法,一共有4种实现。这里是word2vec详细信息。
Skip-gram
对于每个单词\(w_t\),会选择一个上下文窗口\(m\)。 然后要预测出范围内的上下文单词,使概率\(P(w_{t+i} \mid w_t)\)最大。
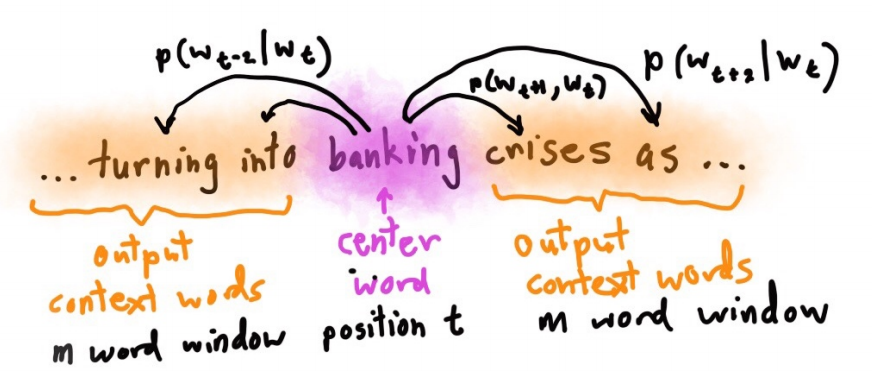
目标函数
\(\theta\)是我们要训练的参数,目标函数就是所有位置预测结果的乘积,最大化目标函数: \[
J^\prime (\theta) = \prod_{t=1}^T \prod_{-m\le j \le m} p(w_{t+j} \mid w_t ;\; \theta), \quad t \neq j
\] 一般使用negative log likelihood :负采样教程。
要最大化目标函数,就得得到损失函数。对于对数似然函数,取其负对数就可以得到损失函数,再最小化损失函数,其中\(T\)是文本长度,\(m\)是窗口大小: \[ J(\theta) = - \frac{1}{T} \sum_{t=1}^T \sum_{-m\le j \le m} \log P(w_{t+j} \mid w_t) \]
- Loss 函数 = Cost 函数 = Objective 函数
- 对于softmax概率分布,一般使用交叉熵作为损失函数
- 单词\(w_{t+j}\)是one-hot编码
- negative log probability
Word2vec细节
词汇和词向量符号说明:
- \(u\) 上下文词向量,向量是\(d\)维的
- \(v\) 词向量
- 中心词汇\(t\),对应的向量是\(v_t\)
- 上下文词汇\(j\) ,对应的词向量是\(u_j\)
- 一共有\(V\)个词汇
计算\(p(w_{t+j} \mid w_t)\), 即: \[ p(w_{j} \mid w_t) = \mathrm{softmax} (u_j^T \cdot v_t) = \frac{\exp(u_j^T \cdot v_t)} {\sum_{i=1}^V \exp(u_i^T \cdot v_t)} \] 两个单词越相似,点积越大,向量点积如下: \[ u^T \cdot v = \sum_{i=1}^M u_i \times v_i \] softmax之所以叫softmax,是因为指数会让大的数越大,小的数越小。类似于max函数。下面是计算的详细信息:
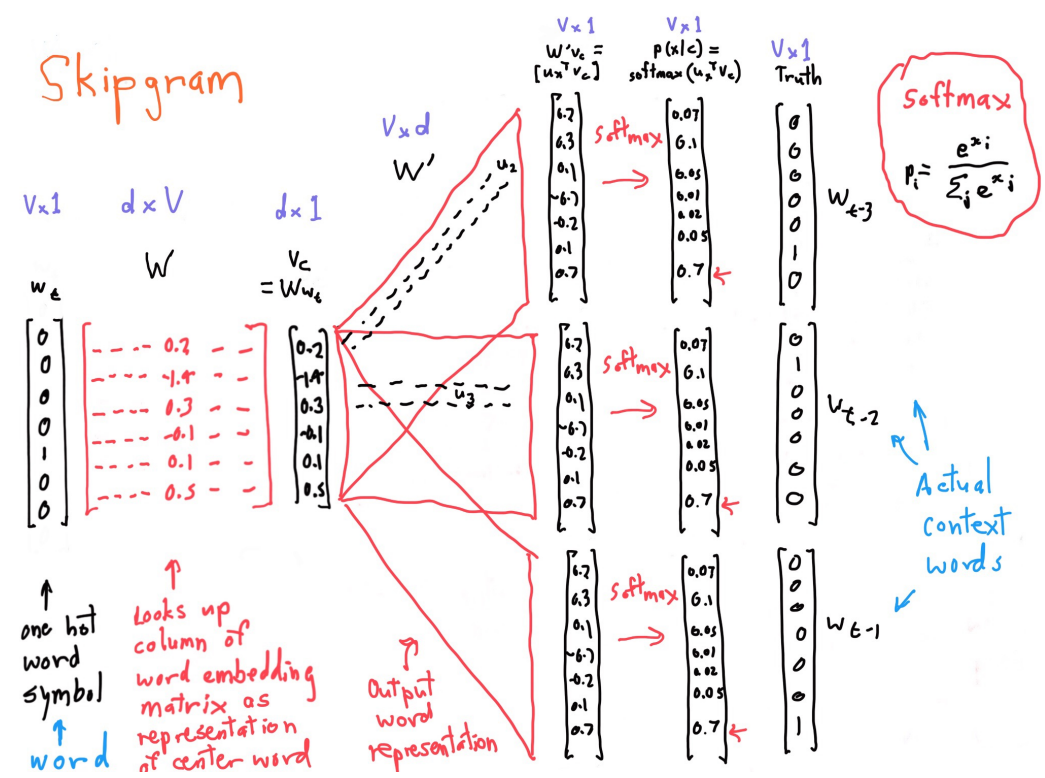
一些理解和解释:
- \(w_t\)是one-hot编码的中心词汇,维数是\((V, 1)\)
- \(W\)是词汇表达矩阵,维数是\((d, V)\),一列就是一个单词
- \(Ww_t = v_t\) 相乘得到词向量\(v_t\) ,\((d, V) \cdot (V, 1) \to (d, 1)\), 用\(d\)维向量去表达了词汇t
- \(W^\prime\), \(W^{\prime}\cdot v_t = s\),\((V, d) \cdot (d, 1) \to (V, 1)\) , 得到 语义相似度向量\(s\)
- 再对\(s\)进行softmax即可求得上下文词汇
- 每个单词有两个向量,作为center单词向量和context单词向量
偏导计算
设\(o\)是上下文单词,\(c\)是中心单词,条件概率如下: \[ P(o \mid c) = \frac{\exp(u_o^T \cdot v_c)} {\sum_{i=1}^V \exp(u_i^T \cdot v_c)} \] 这里只计算\(\log P\)对\(v_c\)向量的偏导。
用\(\mathbf{\theta}\)向量表示所有的参数,有\(V\)个单词,\(d\)维向量。每个单词有2个向量。参数个数一共是\(2dV\)个。
向量偏导计算公式,\(\mathbf{x, a}\) 均是向量 \[
\frac {\partial \mathbf{x}^T \mathbf{a}} { \partial \mathbf{x}}
= \frac {\partial \mathbf{a}^T \mathbf{x}} { \partial \mathbf{x}}
= \mathbf{a}
\] 函数偏导计算,链式法则,\(y=f(u), u=g(x)\) \[
\frac{\mathrm{d}y}{\mathrm{d} x}
= \frac{\mathrm{d}y}{\mathrm{d} u} \frac{\mathrm{d}u}{\mathrm{d} x}
\] 最小化损失函数: \[
J(\theta) = - \frac{1}{T} \sum_{t=1}^T \sum_{-m\le j \le m} \log P(w_{t+j} \mid w_t), \quad j \neq m
\] 这里只计算\(v_c\)的偏导,先进行分解原式为2个部分: \[
\frac { \partial} {\partial v_c} \log P(o \mid c)
= \frac { \partial} {\partial v_c} \log \frac{\exp(u_o^T \cdot v_c)} {\sum_{i=1}^V \exp(u_i^T \cdot v_c)}
= \underbrace { \frac { \partial} {\partial v_c} \log \exp (u_o^T \cdot v_c) }_{1}
- \underbrace { \frac { \partial} {\partial v_c} \log \sum_{i=1}^V \exp(u_i^T \cdot v_c) }_{2}
\] 部分1推导 \[
\begin{align}
\frac { \partial} {\partial v_c} \color{red}{\log \exp (u_o^T \cdot v_c) }
& = \frac { \partial} {\partial v_c} \color{red}{u_o^T \cdot v_c} = \mathbf{u_o}
\end{align}
\] 部分2推导 \[
\begin{align}
\frac { \partial} {\partial v_c} \log \sum_{i=1}^V \exp(u_i^T \cdot v_c)
& = \frac{1}{\sum_{i=1}^V \exp(u_i^T \cdot v_c)} \cdot \color{red}{ \frac { \partial} {\partial v_c} \sum_{x=1}^V \exp(u_x^T \cdot v_c)} \\
& = \frac{1}{A} \cdot \sum_{x=1}^V \color{red} {\frac { \partial} {\partial v_c} \exp(u_x^T \cdot v_c)} \\
& = \frac{1}{A} \cdot \sum_{x=1}^V \exp (u_x^T \cdot v_c) \color{red} {\frac { \partial} {\partial v_c} u_x^T \cdot v_c} \\
& = \frac{1}{\sum_{i=1}^V \exp(u_i^T \cdot v_c)} \cdot \sum_{x=1}^V \exp (u_x^T \cdot v_c) \color{red} {u_x} \\
& = \sum_{x=1}^V \color{red} { \frac{\exp (u_x^T \cdot v_c)} {\sum_{i=1}^V \exp(u_i^T \cdot v_c)}} \cdot u_x \\
& = \sum_{x=1}^V \color{red} {P(x \mid c) }\cdot u_x
\end{align}
\] 所以,综合起来可以求得,单词o是单词c的上下文概率\(\log P(o \mid c)\) 对center向量\(v_c\)的偏导: \[
\frac { \partial} {\partial v_c} \log P(o \mid c)
= u_o -\sum_{x=1}^V P(x \mid c) \cdot u_x
= \color{blue} {\text{观察到的} - \text{期望的}}
\] 实际上偏导是,单词\(o\)的上下文词向量,减去,所有单词\(x\)的上下文向量乘以x作为\(c\)的上下文向量的概率。
总体梯度计算
在一个window里面,对中间词汇\(v_c\)求了梯度, 然后再对各个上下文词汇\(u_o\)求梯度。 然后更新这个window里面用到的参数。
比如句子We like learning NLP。设\(m=1\):
- 中间词汇求梯度 \(v_{like}\)
- 上下文词汇求梯度 \(u_{we}\) 和 \(u_{learning}\)
- 更新参数
梯度下降
有了梯度之后,参数减去梯度,就可以朝着最小的方向走了。机器学习梯度下降 \[ \theta^{new} = \theta^{old} - \alpha \frac{\partial}{\partial \theta^{old}} J(\theta), \quad \quad \theta^{new} = \theta^{old} - \alpha \Delta_{\theta} J(\theta) \] 随机梯度下降
预料会有很多个window,因此每次不能更新所有的。只更新每个window的,对于window t: \[
\theta^{new} = \theta^{old} - \alpha \Delta_{\theta} J_t(\theta)
\]