RNN, LSTM, GRU图文介绍,RNN梯度消失问题等
LSTM经典描述
经典RNN模型
模型
人类在思考的时候,会从上下文、从过去推断出现在的结果。传统的神经网络无法记住过去的历史信息。
循环神经网络是指随着时间推移,重复发生的结构。它可以记住之前发生的事情,并且推断出后面发生的事情。用于处理时间序列很好。所有的神经元共享权值。如下图所示。
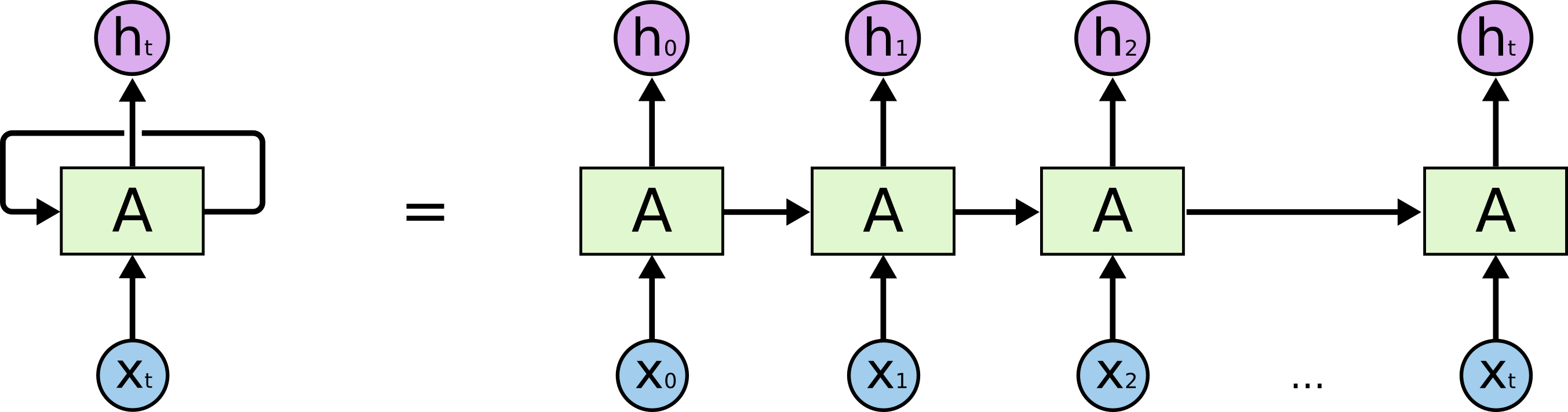
记住短期信息
比如预测“天空中有__”,如果过去的信息“鸟”离当前位置比较近,则RNN可以利用这个信息预测出下一个词为“鸟”
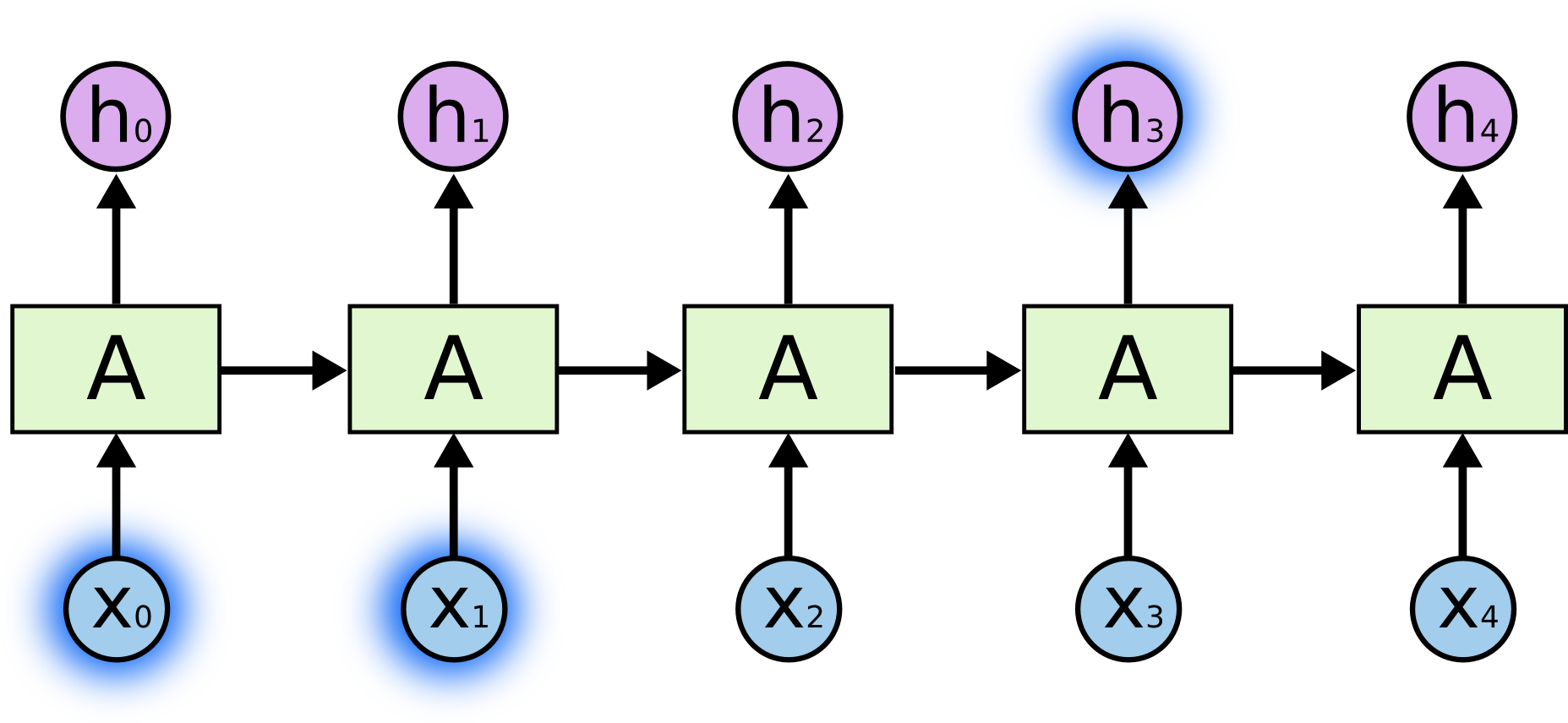
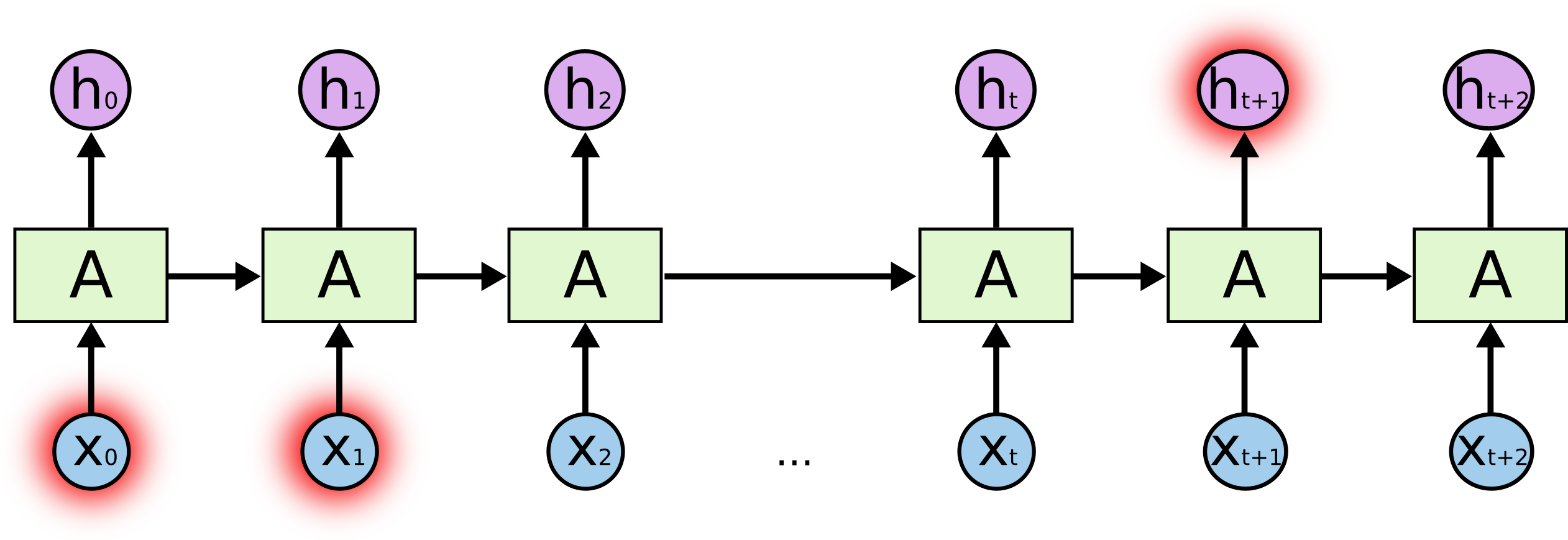
不能长期依赖
如果需要的历史信息距离当前位置很远,则RNN无法学习到过去的信息。这就是不能长期依赖的问题。
LSTM总览与核心结构
- LSTM可以记住一些记忆,捕获长依赖问题
- 也可以让ERROR根据输入,依照不同强度流动
见后面GRU解决梯度消失
总览
所有的RNN有着重复的结构,如下图,比如内部是一个简单的tanh 层。
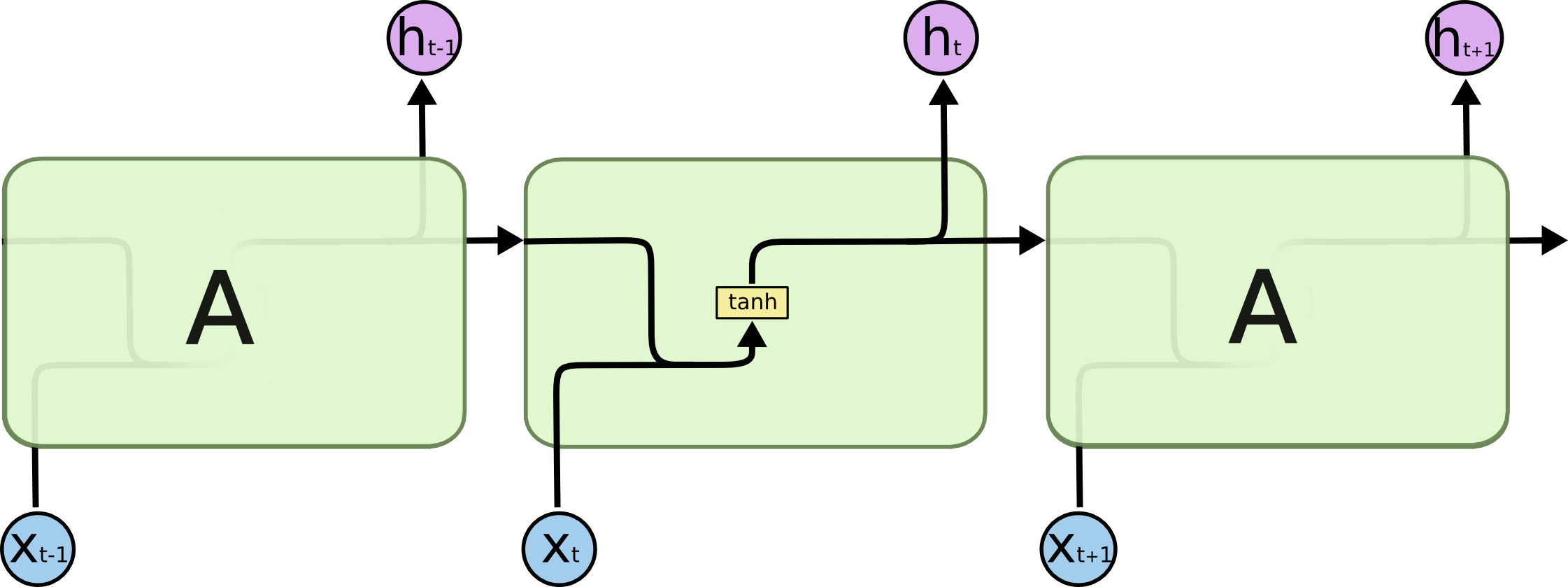
LSTM也是一样的,只不过内部复杂一些。
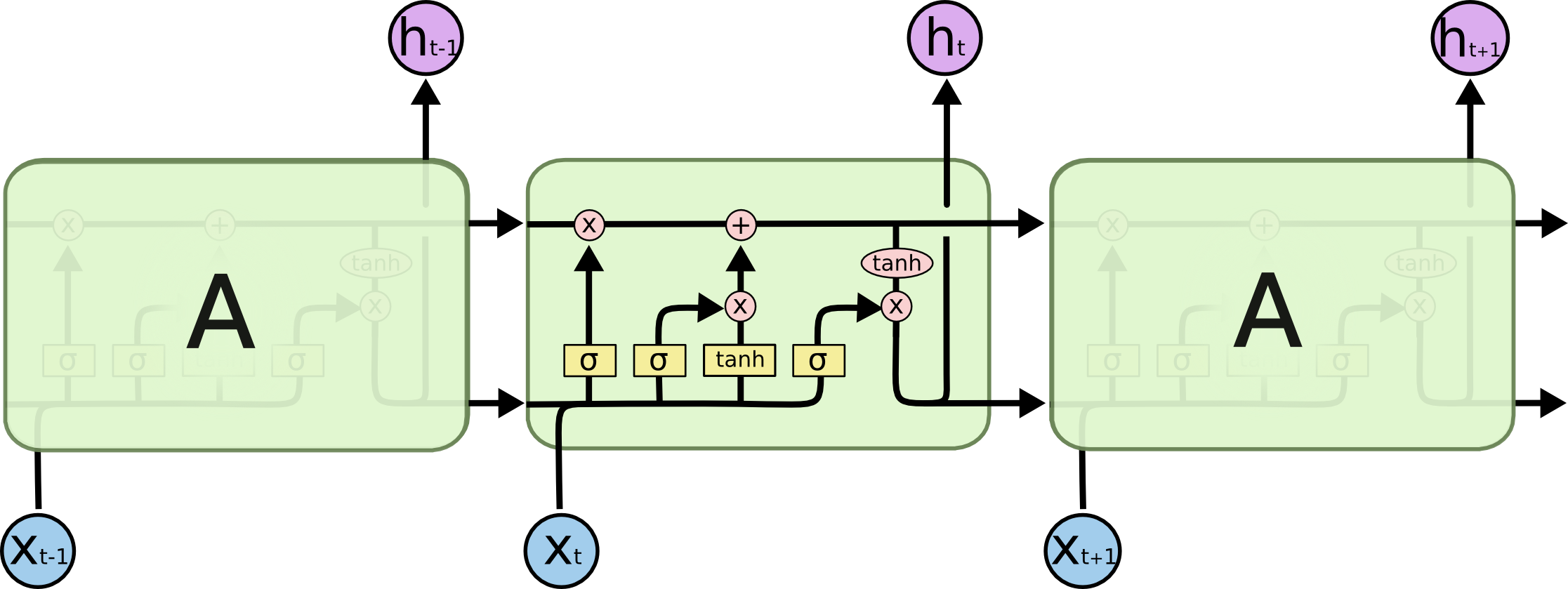
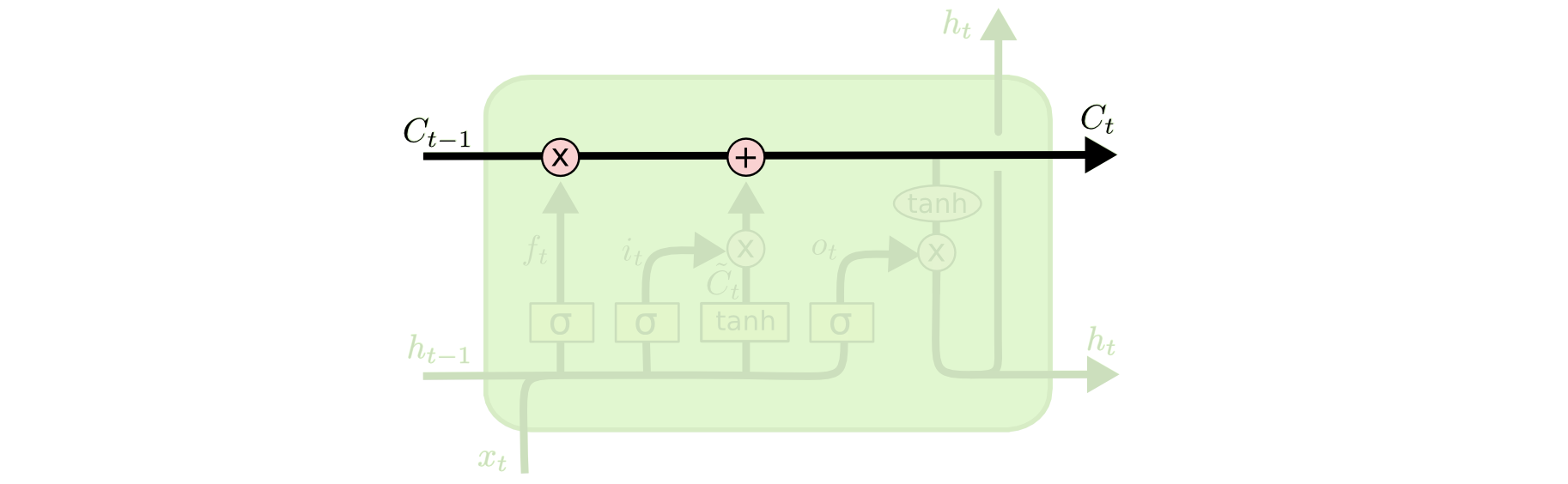
单元状态
单元状态像一个传送带,通过整个链向下运行,只有一些小的线性作用。信息就沿着箭头方向流动。
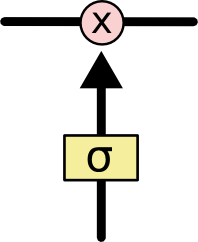
LSTM的门结构
LSTM的门结构 可以添加或者删除单元状态的信息,去有选择地让信息通过。它由sigmoid网络层 和 点乘操作组成。输出属于\([0, 1]\)之间,代表着信息通过的比例。
LSTM细节解剖
一些符号说明,都是\(t\)时刻的信息 :
- \(C_{t-1}\) : 的单元状态
- \(h_{t}\) : 隐状态信息 (也作单个神经元的输出信息)
- \(x_t\) : 输入信息
- \(o_t\) :输出信息 (输出特别的信息)
1 遗忘旧信息
对于\(C_{t-1}\)中的每一个数字, \(h_{t-1}\)和\(x_t\)会输出0-1之间的数来决定遗忘\(C_{t-1}\)中的多少信息。
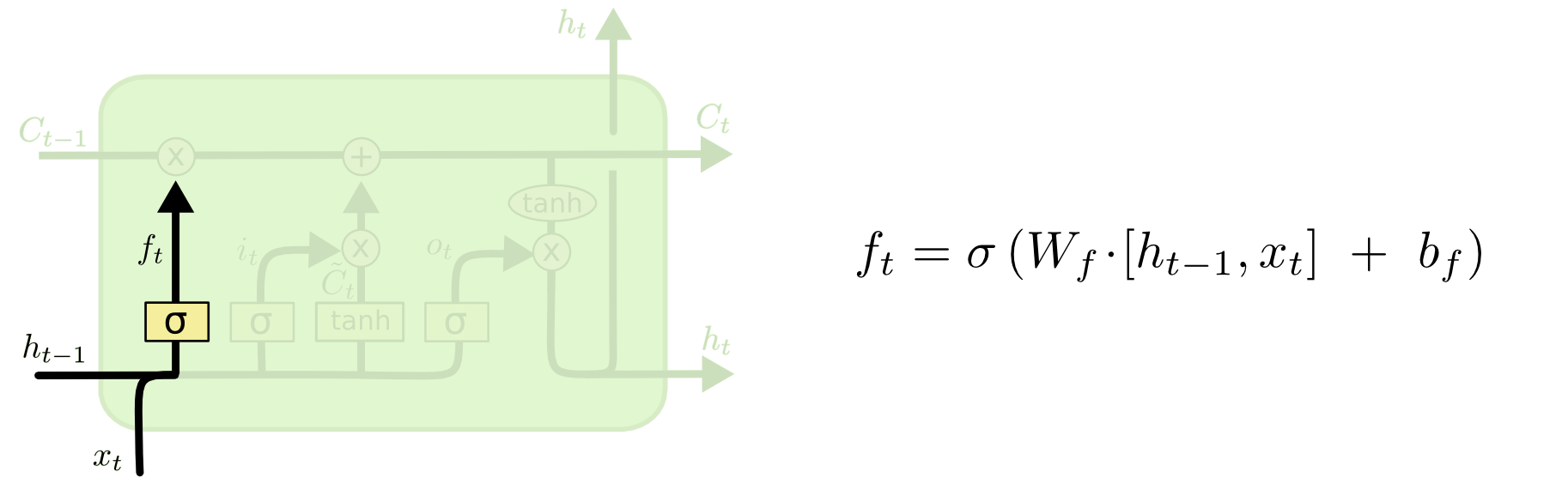
2 生成候选状态和它的更新比例
生成新的状态:tanh层创建新的候选状态\(\hat{C}_t\)
输入门:决定新的状态哪些信息会被更新\(i_t\),即候选状态\(\hat{C}_t\)的保留比例。
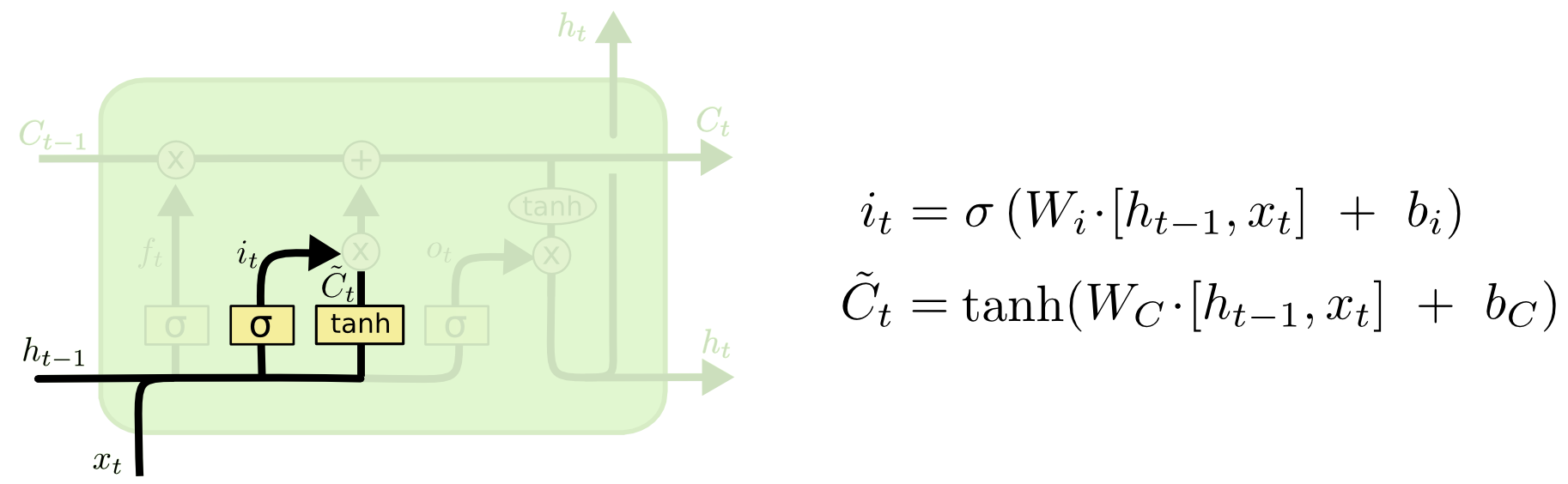
3 新旧状态合并更新
生成新状态\(C_t\):旧状态\(C_{t-1}\) + 候选状态\(\hat{C}_t\)。
旧状态\(C_{t-1}\)遗忘不需要的, 候选状态\(\hat{C}_{t-1}\)保留需要更新的,都是以乘积比例形式去遗忘或者更新。
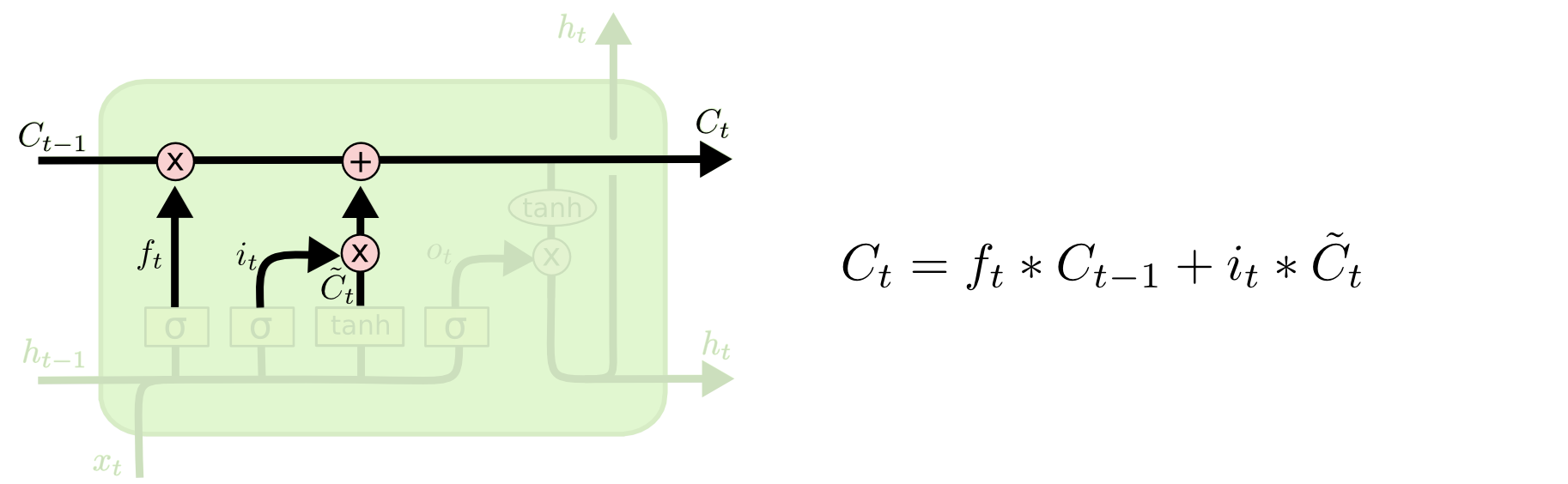
4 输出特别的值
sigmoid:决定单元状态\(C_t\)的哪些信息要输出。
tanh: 把单元状态\(C_t\)的值变到\([-1, 1]\)之间。
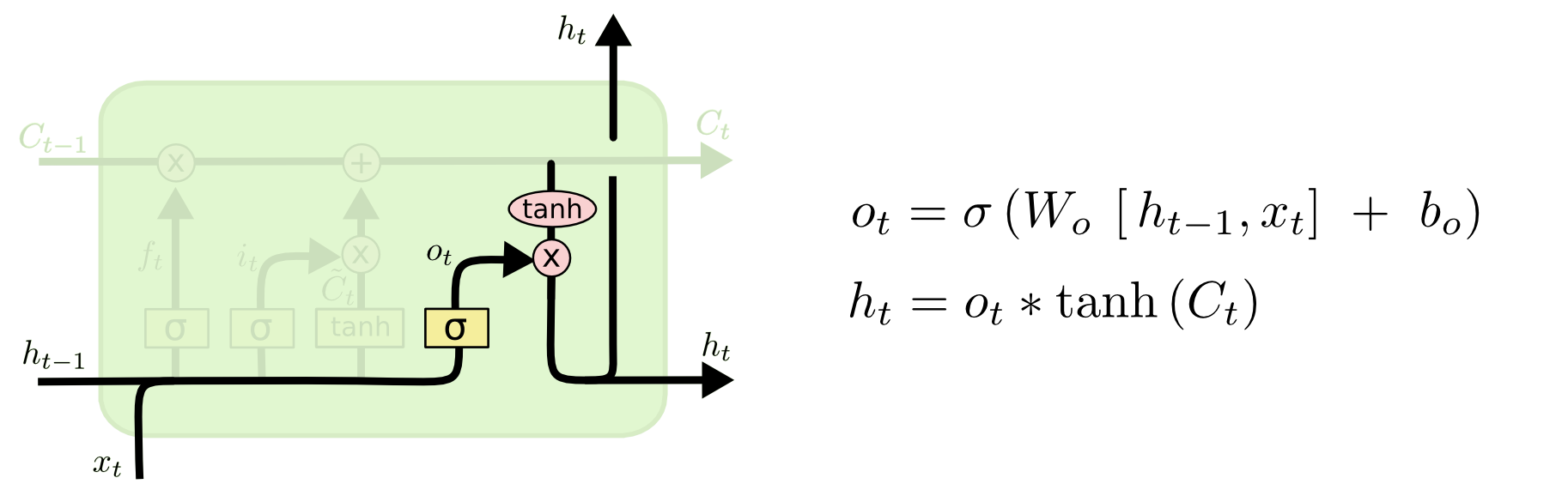
LSTM总结
核心结构如下图所示
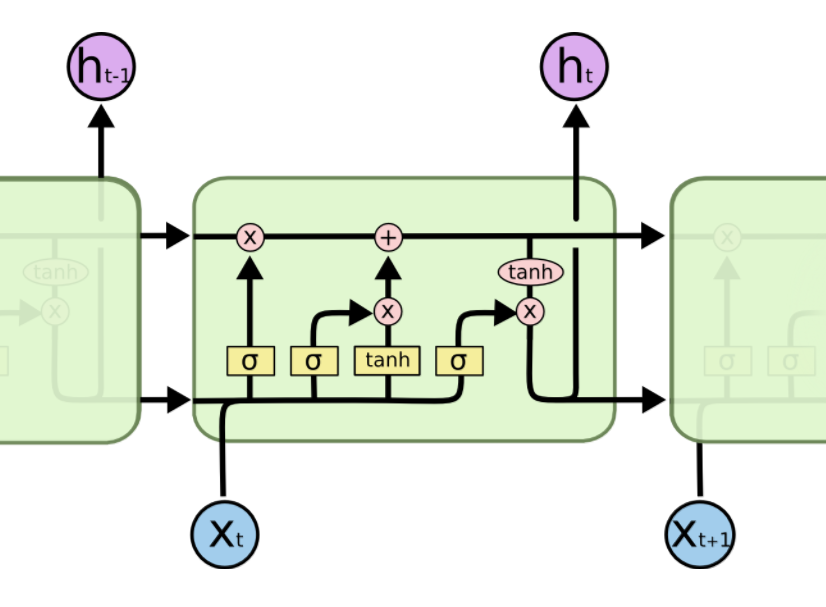
要忘掉部分旧信息,旧信息\(C_{t-1}\)的遗忘比例\(f_t\)
\[
f_t = \sigma (W_f \cdot [h_{t-1}, x_t] + b_f)
\] 新的信息来了,生成一个新的候选\(\hat{C}_t\) \[
\hat{C}_t = \tanh (W_C \cdot [h_{t-1}, x_t] + b_C)
\] 新信息留多少呢,新候选\(\hat C_t\)的保留比例\(i_t\) \[
i_t = \sigma (W_i \cdot [h_{t-1}, x_t] + b_i)
\] 合并旧信息和新信息,生成新的状态信息\(C_t\) \[
C_t = f_t * C_{t-1} + i_t * \hat C_t
\] 输出多少呢,单元状态\(C_t\)的输出比例\(o_t\) \[
o_t = \sigma (W_o \cdot [h_{t-1}, x_t] + b_o)
\] 把\(C_t\)化到\([-1, 1]\)再根据比例输出 \[
h_t = o_t * \tanh(C_t)
\]
图文简介描述LSTM
总体架构
单元架构
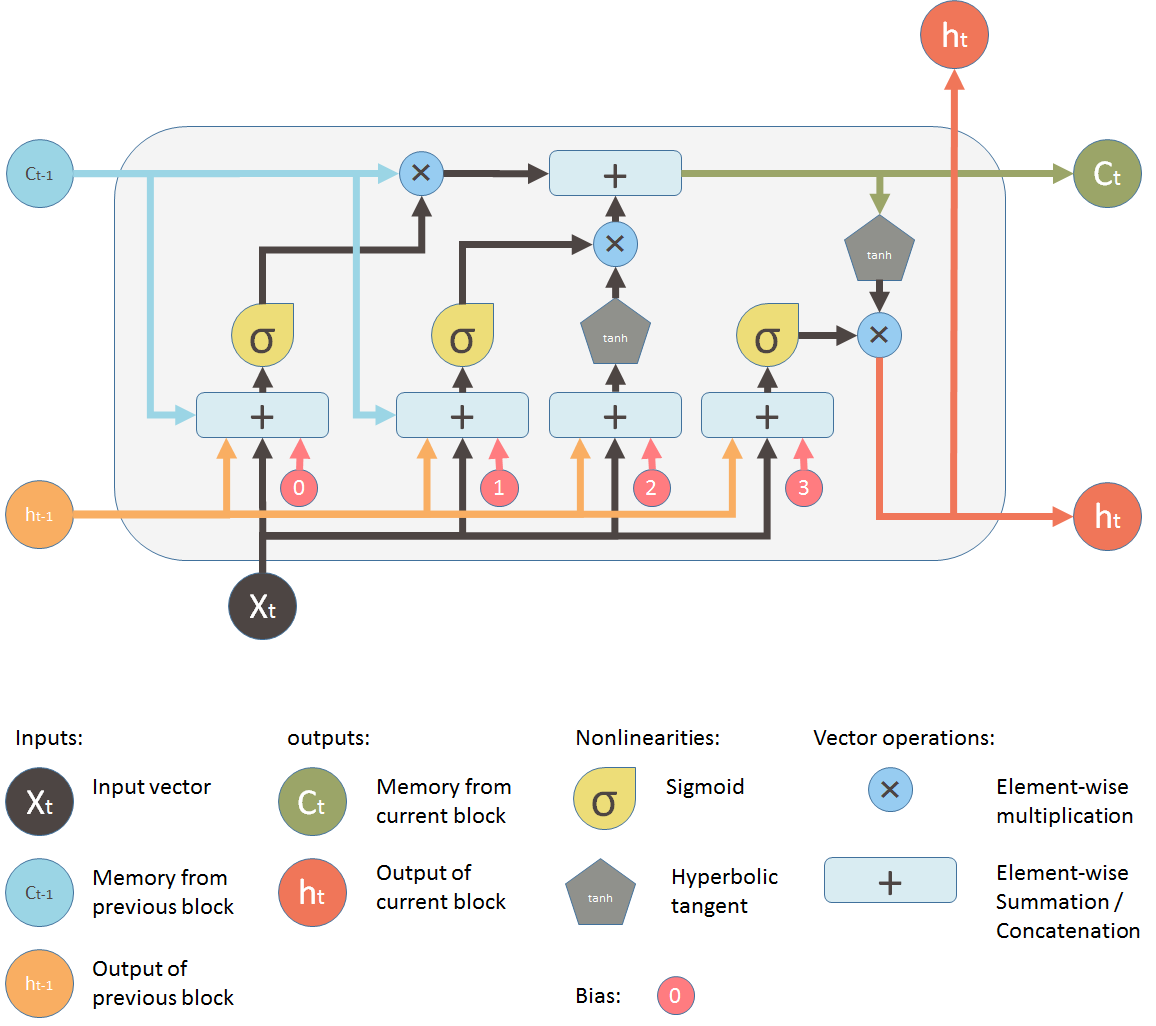
流水线架构

数据流动
圆圈叉叉代表着遗忘\(C_{t-1}\)的信息。乘以向量来实现,向量各个值在\([0, 1]\)之间。 靠近0就代表着遗忘很多,靠近1就代表着保留很多。
框框加号代表着数据的合并。旧信息\(C_{t-1}\)和新候选信息\(\hat C_t\)的合并。 合并之后就得到新信息\(C_t\)。
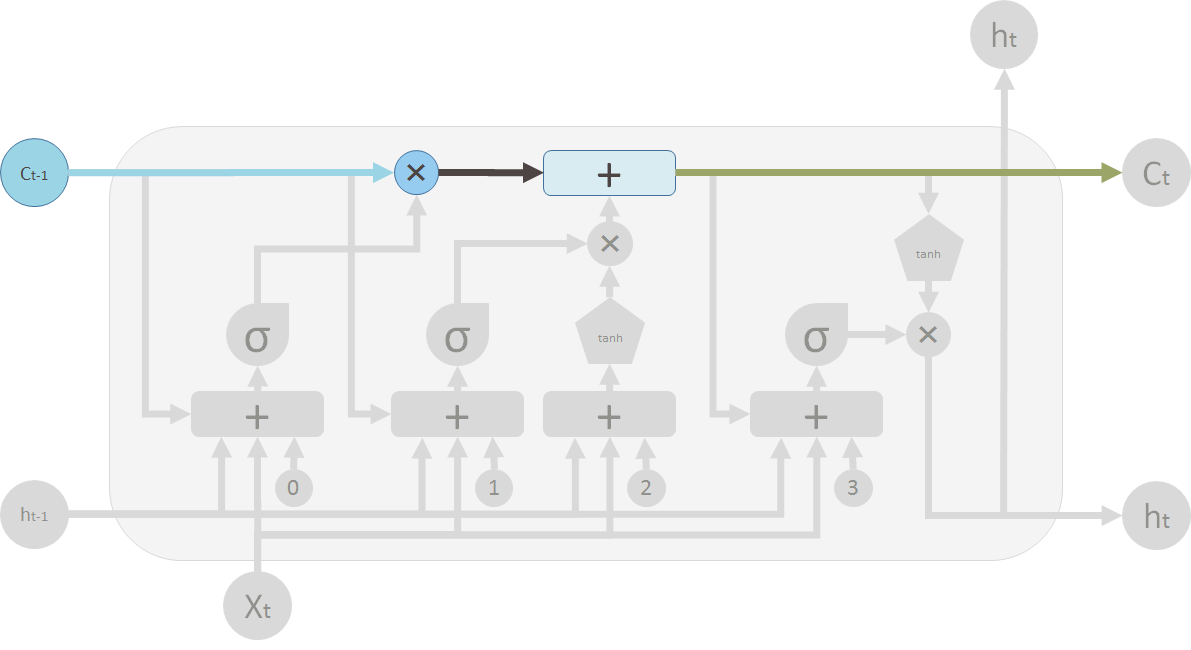
遗忘门
上一个LSTM的输出\(h_{t-1}\) 和 当前的输入\(x_t\),一起作为遗忘门的输入。 0是偏置\(b_0\), 一起做个合并,再经过sigmoid生成遗忘权值\(f_t\)信息, 去遗忘\(C_{t-1}\)。
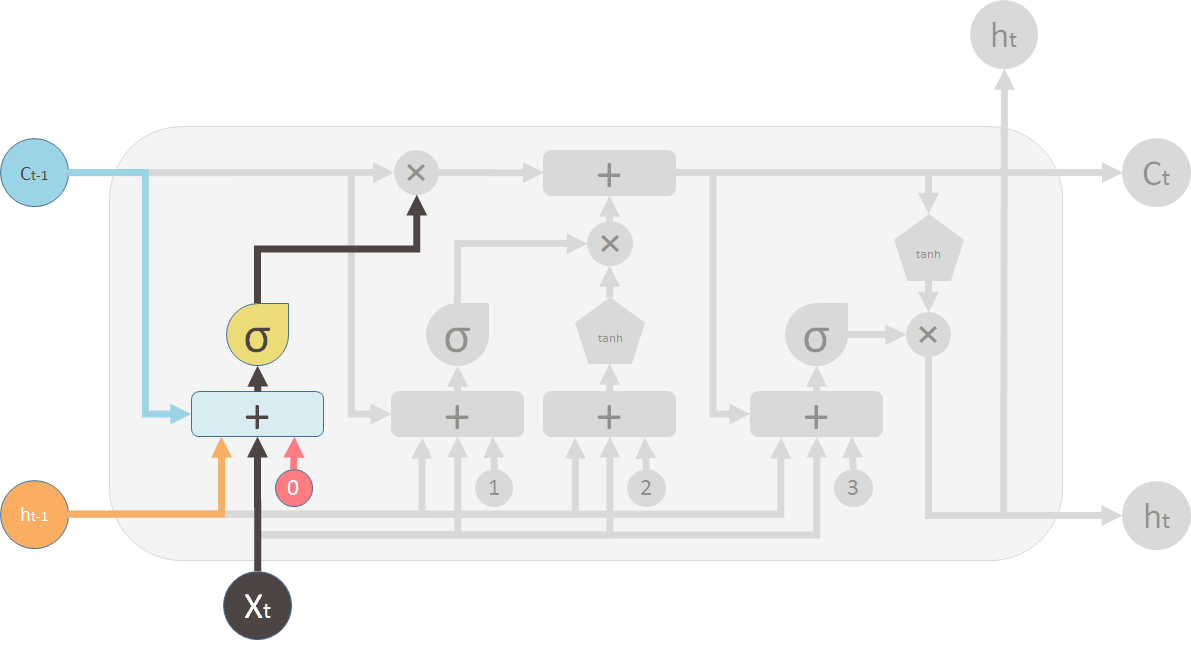
新信息门
新信息门决定着新信息对旧信息的影响力。和遗忘门一样\(h_{t-1}\)和\(x_t\)作为输入。
sigmoid:生成新信息的保留比例。tanh:生成新的信息。
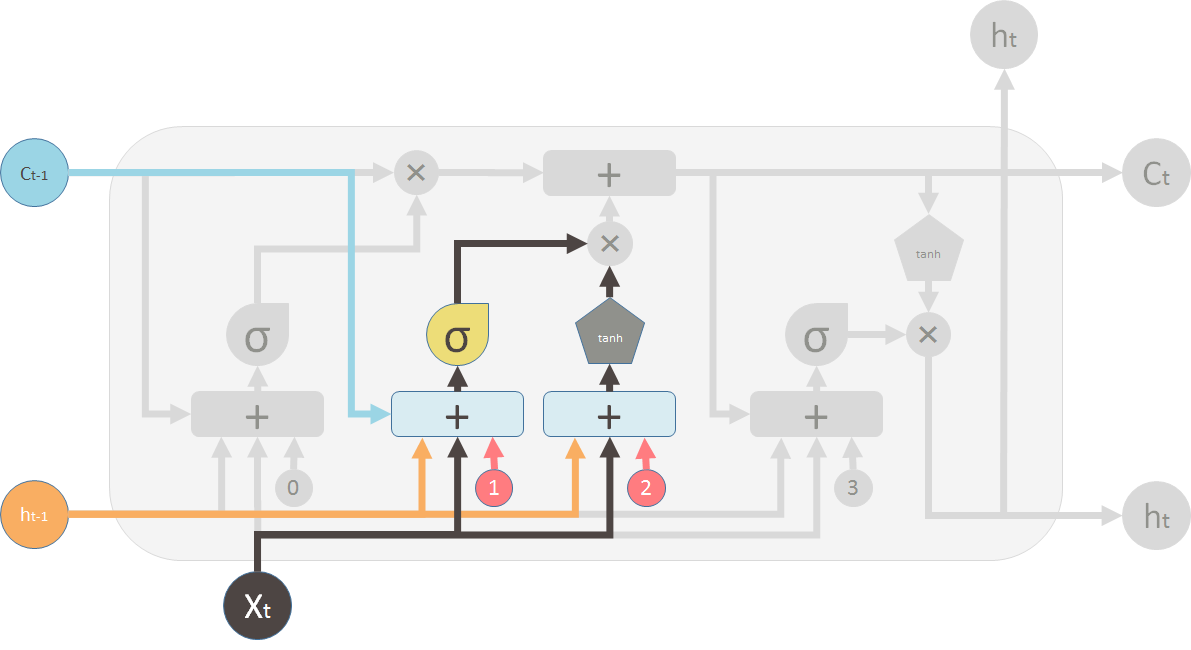
新旧信息合并
旧信息\(C_{t-1}\)和新信息\(\hat{C}_t\)合并,当然分别先过遗忘阀门和更新阀门。
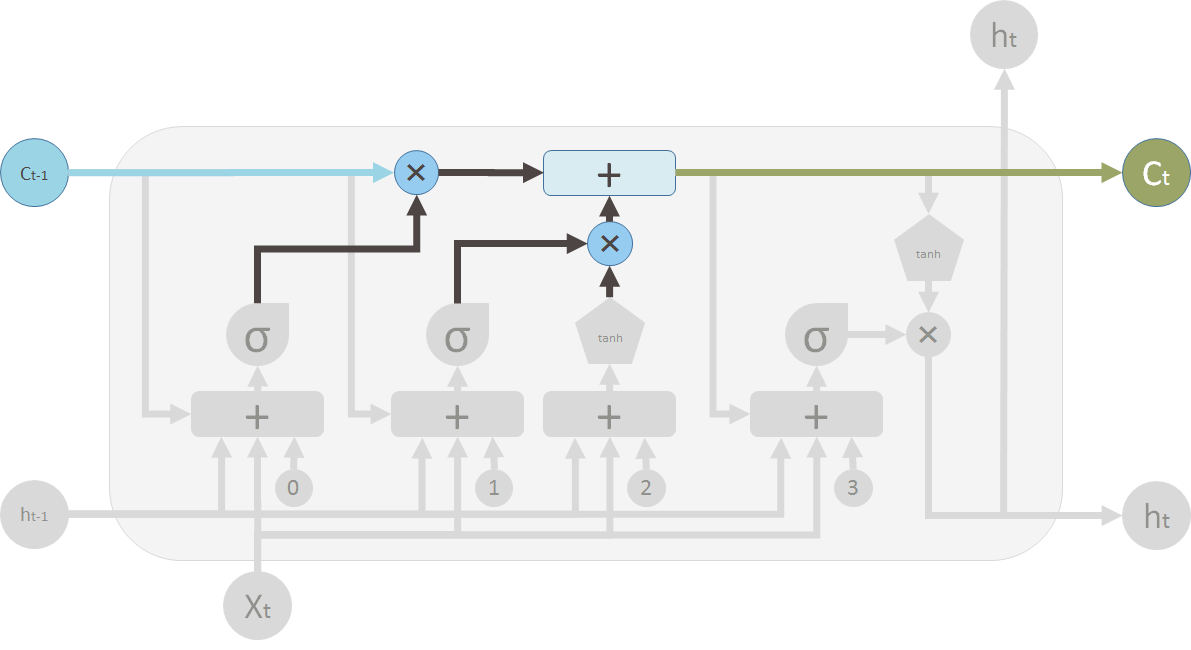
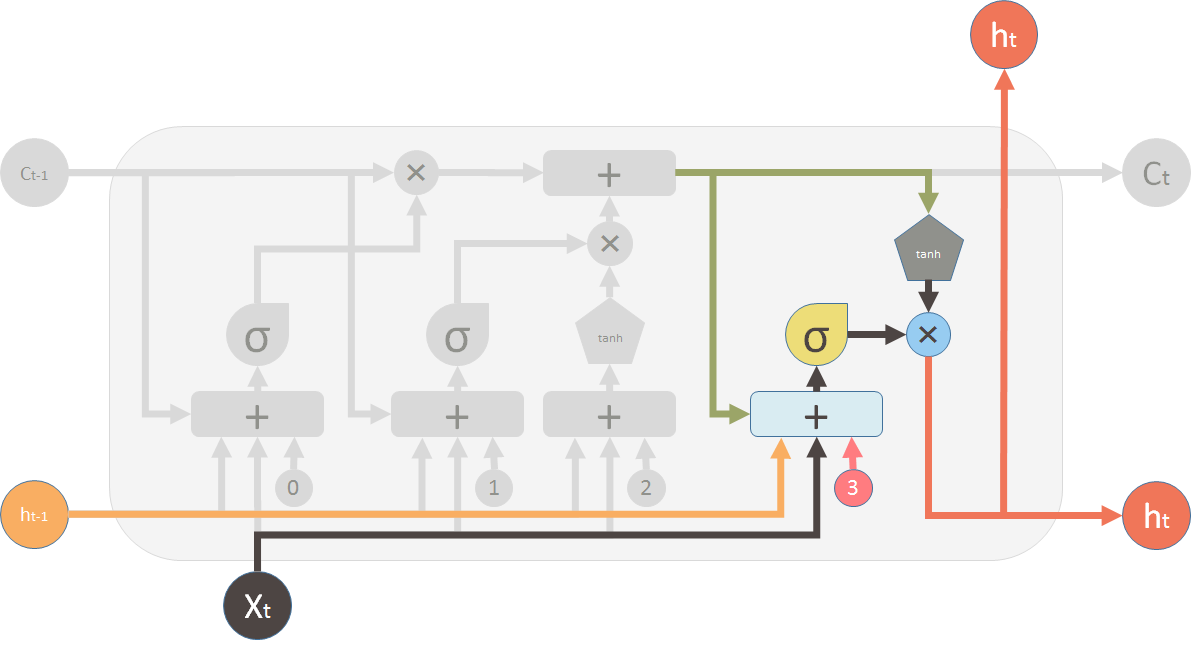
输出特别的值
把新生成的状态信息\(C_t\)使用tanh变成\((-1, 1)\)之间,然后经过输出阀门进行输出。
LSTM变体
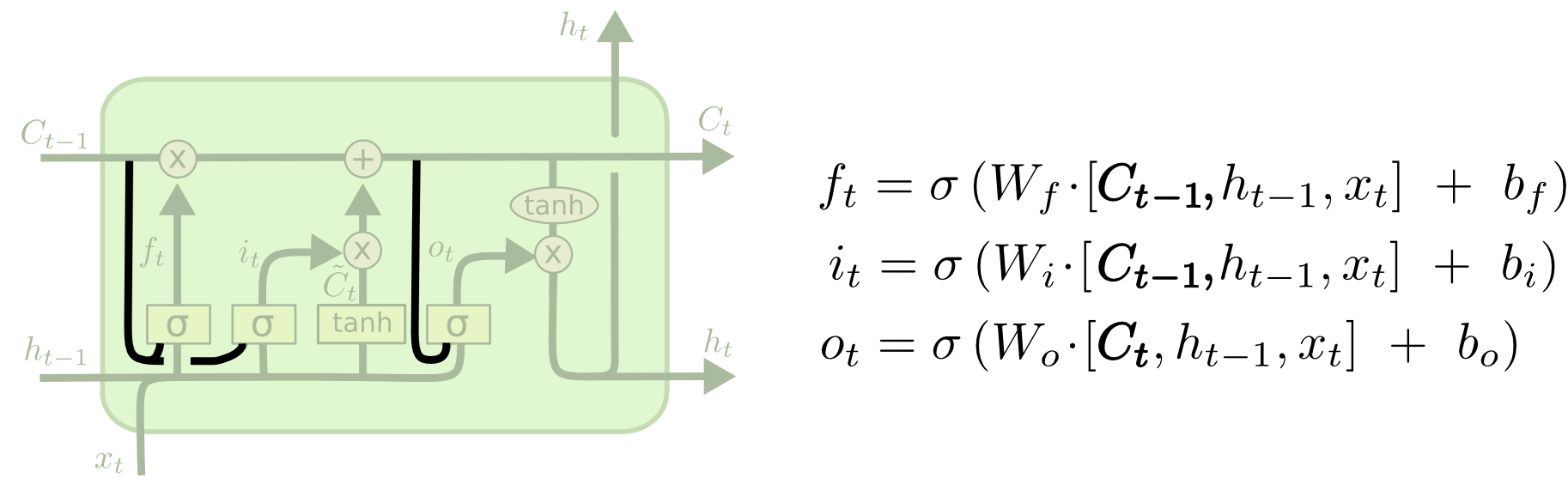
观察口连接
传统LSTM阀门值比例的计算,即更新、遗忘、输出的比例只和\(h_{t-1}, x_t\)有关。
观察口连接,把观察到的单元状态也连接sigmoid上,来计算。即遗忘、更新比例和\(C_{t-1}, h_{t-1}, x_t\)有关,输出的比例和\(C_t, h_{t-1}, x_t\)有关。
组队遗忘
如下图所示,计算好\(C_{t-1}\)的遗忘概率\(i_t\)后,就不再单独计算新候选\(\hat C_t\)的保留概率\(i_t\)。而是直接由1减去遗忘概率得到更新概率。即\(i_t = 1 - f_t\),再去更新。
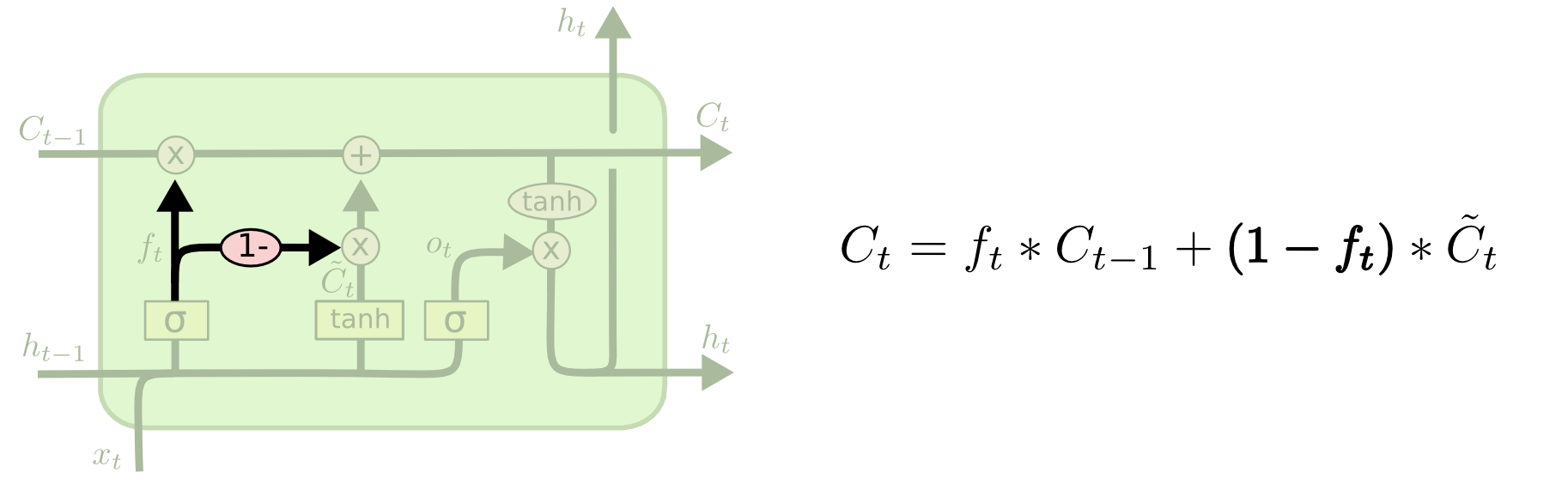
GRU
LSTM有隐状态\(h_t\)和输出状态\(o_t\),而GRU只有\(h_t\),即GRU的隐状态和输出状态是一样的,都用\(h_t\)表示。
更新门\(z_t\)负责候选隐层\(\hat h_t\)保留的比例, \(1-z_t\)负责遗忘旧状态信息\(h_{t-1}\)的比例
\[
z_t = \sigma (W_z \cdot [h_{t-1}, x_t])
\] 候选隐藏层\(\hat h_t\)的计算由\(h_{t-1}\)和\(x_t\)一起计算得到。所以计算\(\hat h_t\)之前,要先计算\(h_{t-1}\)的重置比例。
重置门\(r_t\)负责\(h_{t-1}\)对于生成新的候选\(\hat h_t\)的作用比例 \[
r_t = \sigma (W_r \cdot [h_{t-1}, x_t])
\] 新记忆\(\hat h_t\)的计算 \[
\hat h_t = \tanh (W \cdot [r_t * h_{t-1}, x_t])
\] 最终记忆\(h_t\)由\(h_{t-1}\)和\(\hat h_t\)计算得到,分别的保留比例是\(1-z_t\)和\(z_t\) \[
h_t = (1 - z_t) * h_{t-1} + z_t * \hat h_t
\]

更新门 \(z_t\):过去的信息有多重要。 \(z=1\), 则过去信息非常重要,完全保留下来
重置门\(r_t\): 旧记忆对新记忆的贡献程度。\(r=0\), 则当前新记忆和旧记忆不想关。
RNN梯度问题
RNN梯度推导
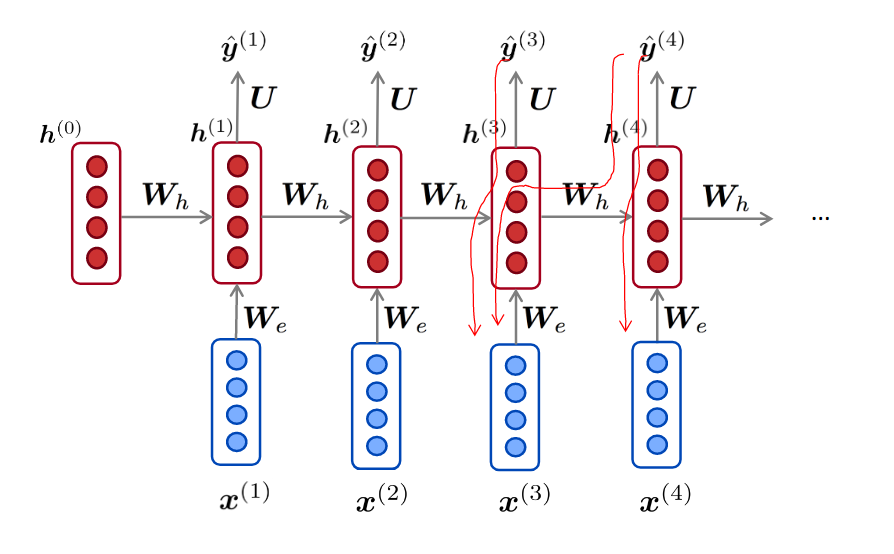
简单点 \[ \begin {align} & h_t = Wh_{t-1} + W^{(hx)} x_t \\ \\ & \hat y_t =W^{(s)} f(h_t) \\ \\ \end{align} \] 总的误差是之前每个时刻的误差之和 \[ \frac{\partial E}{\partial W} = \sum_{t=1}^T \frac{\partial E_t}{\partial W} \] 每一时刻的误差又是之前每个时刻的误差之和,应用链式法则 \[ \frac{\partial E_t}{\partial W} = \frac{\partial E_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \sum_{k=1}^t \frac{\partial h_t}{\partial h_k} \frac{\partial h_k}{\partial W} \]
\[ \frac{\partial E_t}{\partial W} = \sum_{k=1}^t \frac{\partial E_t}{\partial y_t} \frac{\partial y_t}{\partial h_t} \color{blue} {\frac{\partial h_t}{\partial h_k}} \frac{\partial h_k}{\partial W} \]
\[ \frac{\partial E_t}{\partial W} = \sum_{k=1}^t \frac{\partial E_k}{\partial y_k} \frac{\partial y_k}{\partial h_k}\frac{\partial h_k}{\partial h_{k-1}} \frac{\partial h_{k-1}}{\partial W} \]
而\(\frac{\partial h_t}{\partial h_k}\)会变得非常大或者非常小!! \[
\frac{\partial h_t}{\partial h_k} = \prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}}
= \prod_{j=k+1}^t W^T \times \rm{diag}[f^{\prime}(j_{j-1})]
\] 而导数矩阵雅克比矩阵 \[
\frac{\partial h_j}{\partial h_{j-1}} = [ \frac{\partial h_{j}}{\partial h_{j-1,1}}, \cdots , \frac{\partial h_{j}}{\partial h_{j-1,d_h}}]
=
\begin{bmatrix}
\frac{\partial h_{j,1}}{\partial h_{j-1,1}} & \cdots & \frac{\partial h_{j,1}}{\partial h_{j-1,d_h}} \\
\vdots & \ddots & \vdots \\
\frac{\partial h_{j,d_h}}{\partial h_{j-1,1}} & \cdots & \frac{\partial h_{j,d_h}}{\partial h_{j-1,d_h}} \\
\end{bmatrix}
\] 合并起来,得到最终的 \[
\frac{\partial E}{\partial W} = \sum_{t=1}^T\sum_{k=1}^t
\frac{\partial E_t}{\partial y_t}
\frac{\partial y_t}{\partial h_t}
(\prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}})
\frac{\partial h_k}{\partial W}
\] 两个不等式 \[
\| \frac{\partial h_j}{\partial h_{j-1}}\| \le \| W^T\| \cdot \|\rm{diag}[f^{\prime}(h_{j-1})] \| \le \beta_W \beta_h
\] 所以有,会变得非常大或者非常小。会产生梯度消失或者梯度爆炸问题。 \[
\| \frac{\partial h_t}{\partial h_k} \| =\| \prod_{j=k+1}^t \frac{\partial h_j}{\partial h_{j-1}} \|
\le \color{blue}{ (\beta_W \beta_h)^{t-k}}
\] 梯度 是过去对未来影响力的一个度量方法。如果梯度消失了不确定\(t\)和\(k\)之间是否有关系,或者是因为参数错误 。
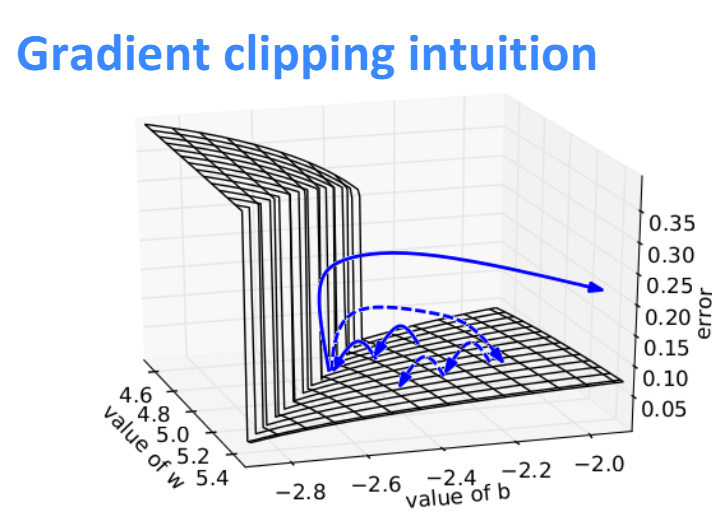
解决梯度爆炸
原始梯度 \[
\mathbf {\hat g} =\frac{\partial E}{\partial W} \\ \\ \\
\] 如果\(\mathbf {\hat g} > 阈值\), 则更新 \[
\mathbf {\hat g} = \frac{\text{threshold}}{\|\mathbf {\hat g}\|} \mathbf {\hat g}
\] 
GRU解决梯度消失
- LSTM可以记住一些记忆,捕获长依赖问题
- 也可以让ERROR根据输入,依照不同强度流动
RNN的前向和反向传播,都会经过每一个节点

GRU可以自动地去创建一些短连接,也可以自动地删除一些不必要的连接。(门的功能)
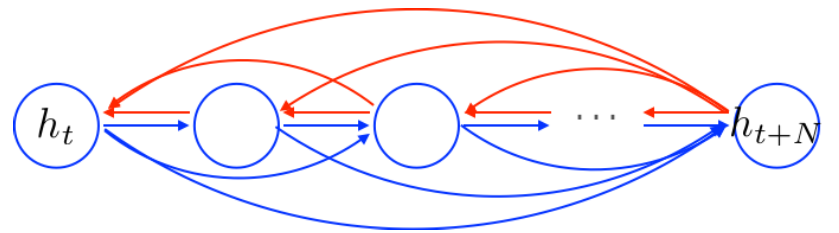
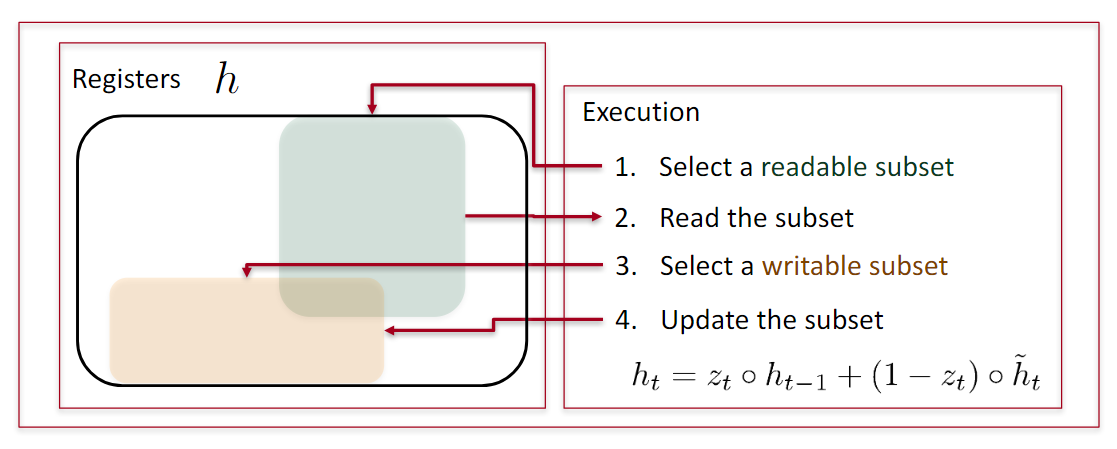
RNN会读取之前所有信息,并且更新所有信息。
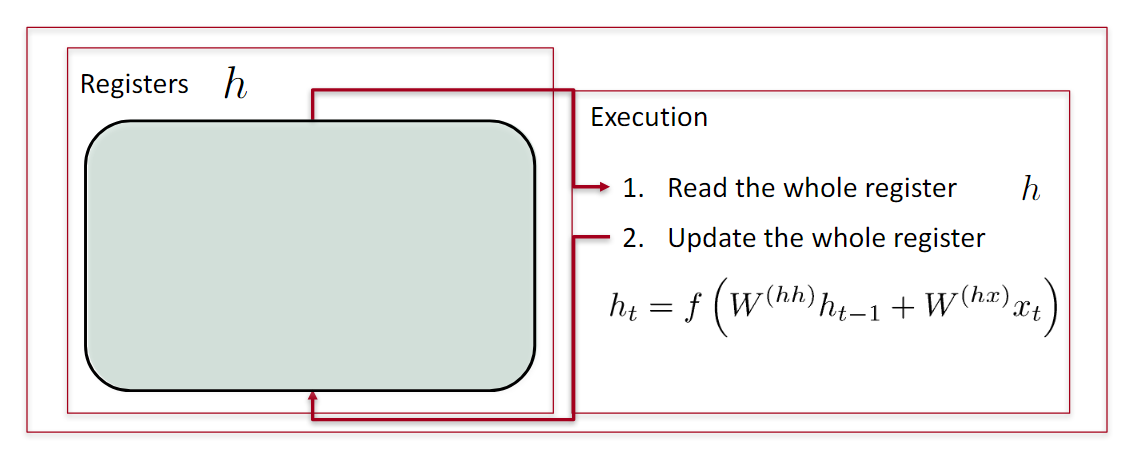
GRU
- 选择可读部分,读取
- 选择可写部分,更新