本文包括概率图模型、马尔科夫模型和隐马尔可夫模型。重点是HMM的前后向算法、维特比算法和BW算法
概述
产生式和判别式
判别方法 由数据直接去学习决策函数\(Y=f(X)\) 或者\(P(Y \mid X)\)作为预测模型 ,即
判别模型
生成方法 先求出联合概率密度\(P(X, Y)\),然后求出条件概率密度\(P(Y \mid X)\)。即
生成模型\(P(Y \mid X) = \frac {P(X, Y)} {P(X)}\)
| 判别式 | 生成式 | |
|---|---|---|
| 原理 | 直接求\(Y=f(X)\) 或\(P(Y \mid X)\) | 先求\(P(X,Y)\),然后 \(P(Y \mid X) = \frac {P(X, Y)} {P(X)}\) |
| 差别 | 只关心差别,根据差别分类 | 关心数据怎么生成的,然后进行分类 |
| 应用 | k近邻、感知机、决策树、LR、SVM | 朴素贝叶斯、隐马尔可夫模型 |
概率图模型
概率图模型(probabilistic graphical models) 在概率模型的基础上,使用了基于图的方法来表示概率分布。节点表示变量,边表示变量之间的概率关系
概率图模型便于理解、降低参数、简化计算,在下文的贝叶斯网络中会进行说明。
贝叶斯网络
贝叶斯网络 又称为信度网络或者信念网络(belief networks),实际上就是一个有向无环图。
节点表示随机变量;边表示条件依存关系。没有边说明两个变量在某些情况下条件独立或者说是计算独立,有边说明任何条件下都不条件独立。
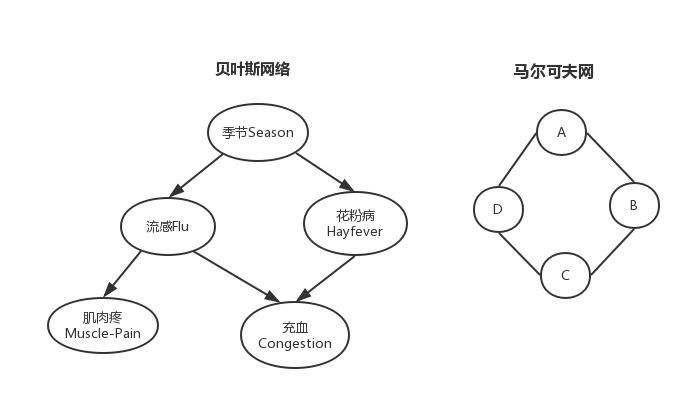
如上图所示,要表示上述情况的概率只需要求出\(4*2*2*2*2-1=63\)个参数的联合概率密度就行了,实际上这个太难以求得。我们可以考虑一下独立关系\((F \perp H \mid S) \,\,\, 表示在S确定的情况下,F和H独立\),所以有以下独立关系: \[ (F \perp H \mid S)、\, (C \perp S \mid F,H)、\, (M \perp H, C \mid F)、 \, (M \perp C | F) \] 所以我们得到如下的计算独立假设: \[ P(C \mid FHS) = P(C \mid FH),即假设C只与FH有关,而与S无关 \] 又由\(P(AB)=P(A|B)P(B)\),所以得到联合概率分布: \[ \begin{align*} P(SFHMC) &= P(M \mid SHFC) \cdot P(SHFC) = \underbrace {P(M \mid F)}_{\color {red}{计算独立性}} \cdot \underbrace {P(C \mid SHF) \cdot P(SHF)}_{\color{red}{继续分解}} \\ &= P(M \mid F) \cdot P(C \mid FH) \cdot P(F \mid S) \cdot P(H \mid S) \cdot P(S) \end{align*} \] \(P(S)\) 4个季节,需要3个参数;\(P(H \mid S)\)时,\(P(Y \mid Spring)\) 和 \(P(N \mid Spring)\)只需要一个参数,所以\(P(H \mid S)\)只需要4个参数即可,其他同理。
所以联合概率密度就转化成了上述公式中的5个乘积项,其中每一项需要的参数个数分别是2、4、4、4、3,所以一共只需要17个参数,这就大大降低了参数的个数。
马尔可夫模型
简介
马尔可夫模型(Markov Model) 描述了一类重要的随机过程,未来只依赖于现在,不依赖于过去。这样的特性的称为马尔可夫性,具有这样特性的过程称为马尔可夫过程。
时间和状态都是离散的马尔可夫过程称为马尔可夫链,简称马氏链,关键定义如下
- 系统有\(N\)个状态\(S = \{ s_1, s_2, \cdots, s_N\}\),随着时间的推移,系统将从某一状态转移到另一状态
- 设\(q_t \in S\)是系统在\(t\)时刻的状态,\(Q = \{q_q, q_2, \cdots, q_T \}\)系统时间的随机变量序列
一般地,系统在时间\(t\)时的状态\(s_j\)取决于\([1, t-1]\)的所有状态\(\{q_1, q_2, \cdots, q_{t-1}\}\),则当前时间的概率是 \[ P(q_t = s_j \mid q_{t-1} = s_i, q_{t-2} = s_k, \cdots) \]
在时刻\(m\)处于\(s_i\)状态,那么在时刻\(m+n\)转移到状态\(s_j\)的概率称为转移概率,即从时刻\(m \to m+n\): \[
\color{blue} {P_{ij}(m, m+n)} = P(q_{m+n} = s_j \mid q_m = s_i)
\]
如果\(P_{ij}(m, m+n)\)只与状态\(i, j\)和步长\(n\)有关,而与起始时间\(m\)无关,则记为\(\color {blue} {P_{ij}(n)}\),称为n步转移概率。 并且称此转移概率具有平稳性,且称此链是齐次的,称为齐次马氏链,我们重点研究齐次马氏链。\(P(n) = [P_{ij}(n)]\)称为n步转移矩阵。 \[
P_{ij}(m, m+n) =\color {blue} {P_{ij}(n)} = P(q_{m+n} = s_j \mid q_m = s_i)
\] 特别地,\(n = 1\)时,有一步转移概率如下 \[
p_{ij} = P_{ij}(1) = P(q_{m+1} \mid q_{m}) = a_{ij}
\]
一阶马尔可夫
特别地,如果\(t\)时刻状态只与\(t-1\)时刻状态有关,那么下有离散的一阶马尔可夫链如下: \[
P(q_t = s_j \mid q_{t-1} = s_i, q_{t-2} = s_k, \cdots) = P(q_t = s_j\mid q_{t-1} = s_i)
\] 其中\(t-1\)的状态\(s_i\)转移到\(t\)的状态\(s_j\)的概率定义如下: \[
P(q_t = s_j\mid q_{t-1} = s_i) = \color{blue} {a_{ij}},其中i, j \in [1, N],a_{ij} \ge 0,\sum_{j=1}^Na_{ij} = 1
\] 显然,\(N\)个状态的一阶马尔可夫链有\(N^2\)次状态转移,这些概率\(a_{ij}\)构成了状态转移矩阵。 \[
A = [a_{ij}] =
\begin{bmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\
a_{21} & a_{22} & \cdots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & \cdots & a_{nn} \\
\end{bmatrix}
\] 设系统在初始状态的概率向量是 \(\color{blue} {\pi_i} \ge 0\) ,其中,\(\sum_{i=1}^{N}\pi_i = 1\)
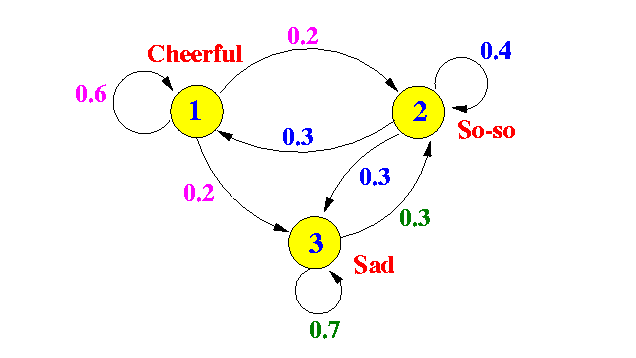
那么时间序列\(Q = \{q_1, q_2, \cdots, q_T \}\)出现的概率是 \[ \color{blue} {P(q_1, q_2, \cdots, q_T) } = P(q_1) P(q2 \mid q_1) P(q_3 \mid q_2) \cdots P(q_T \mid q_{T-1}) = \color{red} {\underbrace {\pi_{q_1}}_{初态概率} \prod_{t=1}^{T-1} a_{q_tq_{t+1}}} \] 下图是一个例子
多步转移概率
对于齐次马氏链,多步转移概率就是\(u+v\)时间段的状态转移,可以分解为先转移\(u\)步,再转移\(v\)步。则有CK方程的矩阵形式 \[
P(u+v) = P(u)P(v)
\] 由此得到\(n\)步转移概率矩阵是一次转移概率矩阵的\(n\)次方 \[
P(n) = P(1) P(n-1) = PP(n-1) \implies P(n) = P^n
\] 对于求矩阵的幂\(A^n\),则最好使用相似对角化来进行矩阵连乘。
存在一个可逆矩阵P,使得\(P^{-1}AP = \Lambda,A = P \Lambda P^{-1}\),其中\(\Lambda\)是矩阵\(A\)的特征值矩阵 \[ \Lambda = \begin{bmatrix} \lambda_1 & & & \\ &\lambda_2 & & \\ && \ddots & \\ & & & \lambda_n \\ \end{bmatrix} ,其中\lambda是矩阵A的特征值 \] 则有\(A^n = P\Lambda ^ {n}P^{-1}\)
遍历性
齐次马氏链,状态\(i\)向状态\(j\)转移,经过无穷步,任何状态\(s_i\)经过无穷步转移到状态\(s_j\)的概率收敛于一个定值\(\pi_j\),即\(\lim_{n \to \infty} P_{ij}(n) = \pi_j \; (与i无关)\) 则称此链具有遍历性。若\(\sum_{j=1}^N \pi_j = 1\),则称\(\vec{\pi} = (\pi_1, \pi_2, \cdots)\)为链的极限分布。
遍历性的充分条件:如果存在正整数\(m\)(步数),使得对于任意的,都有如下(转移概率大于0),则该马氏链具有遍历性 \[ P_{ij}(m) > 0, \quad i, j =1, 2, \cdots, N, \quad s_i,s_j \in S \; \] 那么它的极限分布\(\vec{\pi} = (\pi_1, \pi_2, \cdots, \pi_N)\),它是下面方程组的唯一解 \[ \pi = \pi P, \quad 即\pi_j = \sum_{i=1}^{N} \pi_i p_{ij}, \quad 其中\pi_j > 0, \sum_{j=1}^N \pi_j = 1 \]
PageRank应用
有很多应用,压缩算法、排队论等统计建模、语音识别、基因预测、搜索引擎鉴别网页质量-PR值。
Page Rank算法
这是Google最核心的算法,用于给每个网页价值评分,是Google“在垃圾中找黄金”的关键算法。
大致思想是要为搜索引擎返回最相关的页面。页面相关度是由和当前网页相关的一些页面决定的。
当前页面会把自己的
importance平均传递给它所指向的页面,若有\(k\)个,则为每个传递\(\frac 1 k\)- 如果有很多页面都指向当前页面,则当前页面很重要,相关度高
当前页面有一些来自官方页面的
backlink,当前页面很重要
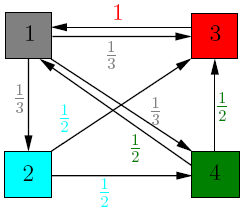
例如有4个页面,分别如下
矩阵\(\color {blue }A\)是页面跳转的一次转移矩阵,\(\color {blue }q\)是当前时间每个页面的相关度向量,即PageRank vector。 \[
A =
\begin{bmatrix}
0 & 0 &1 & \frac {1}{2} \\
\frac {1}{3}& 0 & 0 & 0 \\
\frac {1}{3}& \frac {1}{2} & 0 & \frac {1}{2} \\
\frac {1}{3} & \frac {1}{2} & 0 & 0 \\
\end{bmatrix}
\quad
初始时刻,q =
\begin {bmatrix}
\frac1 4 \\
\frac1 4 \\
\frac1 4 \\
\frac1 4 \\
\end {bmatrix}
\] \(A\)的一列是当前页面出去的所有页面,一行是进入当前页面的所有页面。设\(u\)表示第\(A\)的第\(i\)行,那么\(u*q\)就表示当页面\(i\)接受当前\(q\)的更新后的rank值。
定义矩阵\(\color {blue} {G} = \color{red} {\alpha A + (1-\alpha) \frac {1} {n} U}\),对\(A\)进行修正,\(G\)所有元素大于0,具有遍历性
- \(\alpha \in[0, 1] \; (\alpha = 0.85)\) 阻尼因子
- \(A\) 一步转移矩阵
- \(n\) 页面数量
- \(U\) 元素全为\(1\)的矩阵
使用\(G\)进行迭代的好处
- 解决了很多\(A\)元素为0导致的问题,如没有超链接的节点,不连接的图等
- \(A\)所有元素大于0,具有遍历性,具有极限分布,即它的极限分布\(q\)会收敛
那么通过迭代就可以求出PR向量\(\color {red} {q^{next} = G q^{cur}}\),实际上\(q\)是\(G\)的特征值为1的特征向量。
迭代具体计算如下图(下图没有使用G,是使用A去算的,这是网上找的图[捂脸])
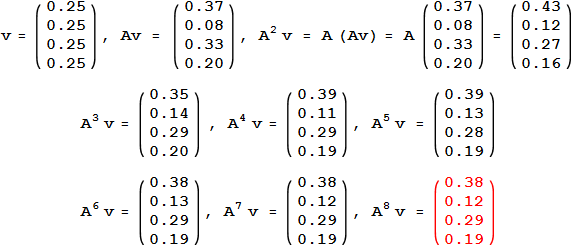
随着迭代,\(q\)会收敛,那么称为\(q\)就是PageRank vector。
我们知道节点1有2个backlink,3有3个backlink。但是节点1却比3更加相关,这是为什么呢?因为节点3虽然有3个backlink,但是却只有1个outgoing,只指向了页面1。这样的话它就把它所有的importance都传递给了1,所以页面1也就比页面3的相关度高。
隐马尔可夫模型
定义
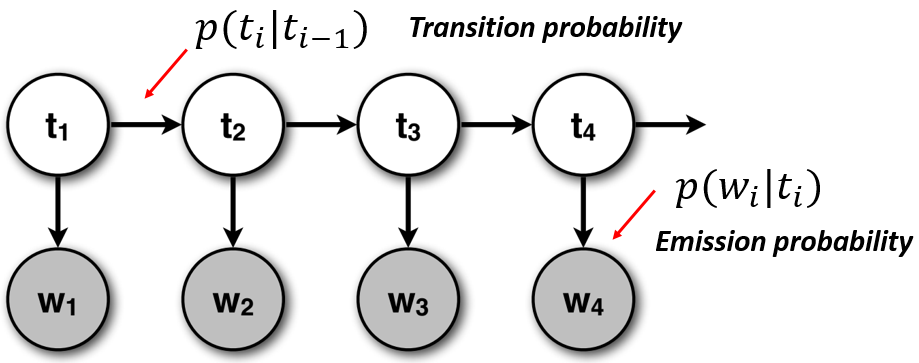
隐马尔可夫模型(Hidden Markov Model, HMM)是统计模型,它用来描述含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来做进一步的分析。大概形状如下
一个HMM由以下5个部分构成。
隐藏状态
模型的状态,隐蔽不可观察- 有\(N\)种,隐状态种类集合\(\color {blue} {S = \{s_1, s_2, \cdots, s_N\}}\)会相
- 隐藏状态互相互转换,一步转移。\(s_i\)转移到\(s_j\)的概率 \(\color {red} {a_{ij} = P(q_t= s_j \mid q_{t-1}=s_i)}\)
- \(q_t = s_i\) 代表在\(t\)时刻,系统隐藏状态\(q_t\)是\(s_i\)
隐状态时间序列\(\color{blue}{Q = \{q_1, q_2, \cdots, q_t, q_{t+1}\cdots \}}\)
观察状态
- 模型可以显示观察到的状态
- 有\(M\)种,显状态种类集合\(\color{blue} {K = \{v_1, v_2, \cdots, v_M\}}\)。不能相互转换,只能由隐状态产生(发射)
- \(o_t = v_k\) 代表在\(t\)时刻,系统的观察状态\(o_t\)是\(v_k\)
- 每一个隐藏状态会发射一个观察状态。\(s_j\)发射符号\(v_k\)的概率\(\color {red} {b_j (k) = P(o_t = v_k \mid s_j)}\)
显状态时间序列\(\color{blue} {O = \{o_1, o_2, \cdots, o_ t\}}\)
状态转移矩阵A (隐--隐)
- 从一个隐状\(s_i\)转移到另一个隐状\(s_j\)的概率。\(A = \{a_{ij}\}\)
- \(\color {red} {a_{ij} = P(q_t= s_j \mid q_{t-1}=s_i)}\),其中 \(1 \leq i, j \leq N, \; a_{ij} \geq 0, \; \sum_{j=1}^N a_{ij}=1\)
发射概率矩阵B (隐--显)
- 一个隐状\(s_j\)发射出一个显状\(v_k\)的概率。\(B = \{b_j(k)\}\)
- \(\color {red} {b_j(k) = P(o_t = v_k \mid s_j)}\),其中\(1 \leq j \leq N; \; 1 \leq k \leq M; \; b_{jk} \ge 0; \; \sum_{k=1}^Mb_{jk}=1\)
初始状态概率分布 \(\pi\)
- 最初的隐状态\(q_1=s_i\)的概率是\(\pi_i = P(q_1 = s_i)\)
- 其中\(1 \leq i \leq N, \; \pi_i \ge 0, \; \sum_{i=1}^N \pi_i = 1\)
一般地,一个HMM记作一个五元组\(\mu = (S, K, A, B, \pi)\),有时也简单记作\(\mu = (A, B, \pi)\)。一般,当考虑潜在事件随机生成表面事件的时候,HMM是非常有用的。
HMM中的三个问题
观察序列概率给定观察序列\(O=\{o_1, o_2, \cdots, o_T\}\)和模型\(\mu = (A, B, \pi)\),求当前观察序列\(O\)的出现概率\(P(O \mid \mu)\)状态序列概率给定观察序列\(O=\{o_1, o_2, \cdots, o_T\}\)和模型\(\mu = (A, B, \pi)\),求一个最优的状态序列\(Q=\{q_1, q_2, \cdots, q_T\}\)的出现概率,使得最好解释当前观察序列\(O\)训练问题或参数估计问题给定观察序列\(O=\{o_1, o_2, \cdots, o_T\}\),调节模型\(\mu = (A, B, \pi)\)参数,使得\(P(O \mid u)\)最大
前后向算法
给定观察序列\(O=\{o_1, o_2, \cdots, o_T\}\)和模型\(\mu = (A, B, \pi)\),求给定模型\(\mu\)的情况下观察序列\(O\)的出现概率。这是解码问题。如果直接去求,计算量会出现指数爆炸,那么会很不好求。我们这里使用前向算法和后向算法进行求解。
前向算法
前向变量\(\color {blue} {\alpha_t(i)}\)是系统在\(t\)时刻,观察序列为\(O=o_1o_2\cdots o_t\)并且隐状态为\(q_t = s_i\)的概率,即 \[
\color {red} {\alpha_t(i) = P(o_1o_2\cdots o_t, q_t = s_i \mid \mu)}
\] \(\color {blue} {P(O \mid \mu)}\) 是在\(t\)时刻,状态\(q_t=\) 所有隐状态的情况下,输出序列\(O\)的概率之和 \[
\color {blue} {P(O \mid \mu)} = \sum_{i=1}^N P(O, q_t = s_i \mid \mu) = \color {red} {\sum_{i=1}^{N}\alpha_t(i)}
\]
接下来就是计算\(\color {blue} {\alpha_t(i)}\),其实是有动态规划的思想,有如下递推公式 \[ \color {blue} {\alpha_{t+1}(j)} = \color{red}{\underbrace{\left( \sum_{i=1}^N \alpha_t(i)a_{ij} \right)}_{所有状态i转为j的概率} \underbrace {b_j(o_{ t+1})}_{状态j发射o_{t+1}}} \] 上述计算,其实是分为了下面3步
- 从1到达时间\(t\),状态为\(s_i\),输出\(o_1o_2 \cdots o_t\)。\(\color{blue}{\alpha_t(i)}\)
- 从\(t\)到达\(t+1\),状态变化\(s_i \to s_j \text{。} \quad\color{blue}{a_{ij}}\)
- 在\(t+1\)时刻,输出\(o_{t+1}\)。\(\color{blue}{b_j(o_{ t+1})}\)
算法的步骤如下
- 初始化 \(\color {blue} {\alpha_1(i)} = \color {red} {\pi_ib_i(o_1)}, \; 1 \leq i \leq N\)
- 归纳计算 \(\color {blue} {\alpha_{t+1}(j)} = \color{red} {\left( \sum_{i=1}^N \alpha_t(i)a_{ij} \right) b_j(o_{ t+1})}, \; 1 \leq t \leq T-1\)
- 求和终结 \(\color {blue} {P(O \mid \mu)} = \color {red} {\sum_{i=1}^{N}\alpha_T(i)}\)
在每个时刻\(t\),需要考虑\(N\)个状态转移到\(s_{j}\)的可能性,同时也需要计算\(\alpha_t(1), \cdots , \alpha_t(N)\),所以时间复杂度为\(O(N^2)\)。同时在系统中有\(T\)个时间,所以总的复杂度为\(O(N^2T)\)。
后向算法
后向变量 \(\color {blue} {\beta_{t}(i)}\) 是系统在\(t\)时刻,状态为\(s_i\)的条件下,输出为\(o_{t+1}o_{t+2}\cdots o_T\)的概率,即 \[
\color {red} {\beta_t(i) = P(o_{t+1}o_{t+2}\cdots o_T \mid q_t = s_i , \mu)}
\] 递推 \(\color {blue} {\beta_{t}(i)}\)的思路及公式如下
- 从\(t \to t+1\),状态变化\(s_i \to s_j\),并从\(s_j \implies o_{t+1}\),发射\(o_{t+1}\)
- 在\(q_{t+1}=s_j\)的条件下,输出序列\(o_{t+2}\cdots o_T\)
\[ \color {blue} {\beta_{t}(i)} = \sum_{j=1}^N\color{red}{\underbrace {a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}_{s_i转s_j \; s_j发o_{t+1} \; t+1时s_j后面\{o_{t+2}, \cdots\}} } \]
上面的公式个人的思路解释如下(不明白公式再看)
- 其实要从\(\beta_{t+1}(j) \to \beta_{t}(i)\)
- \(\beta_{t+1}(j)\)是\(t+1\)时刻状态为\(s_j\),后面的观察序列为\(o_{t+2}, \cdots, o_{T}\)
- \(\beta_{t}(i)\)是\(t\)时刻状态为\(s_i\),后面的观察序列为\(\color{red}{o_{t+1}}, o_{t+2}, \cdots, o_{T}\)
- \(t \to t+1\) \(s_i\)会变成各种\(s_j\),\(\beta_t(i)\)只关心t+1时刻的显示状态为\(o_{t+1}\),而不关心隐状态,所以是所有隐状态发射\(o_{t+1}\)的概率和
- \(\color{red} {a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}\),\(s_i\)转为\(s_j\)的概率,在t+1时刻\(s_j\)发射\(o_{t+1}\)的概率,t+1时刻状态为\(s_j\) 观察序列为\(o_{t+2}, \cdots, o_{T}\)的概率
- 把上述概率加起来,就得到了t时刻为\(s_i\),后面的观察为\(o_{t+1}, o_{t+2}, \cdots, o_{T}\)的概率\(\beta_{t}(i)\)
上式是把所有从\(t+1 \to t\)的概率加起来,得到\(t\)的概率。算法步骤如下
- 初始化 \(\color {blue} {\beta_T(i) = 1}, \; 1 \leq i \leq N\)
- 归纳计算 \(\color {blue} {\beta_{t}(i)} = \sum_{j=1}^N\color{red}{a_{ij}b_j(o_{t+1})\beta_{t+1}(j) }, \quad 1 \leq t \leq T-1; \; 1 \leq i \leq N\)
- 求和终结 \(\color {blue} {P(O \mid \mu)} = \sum_{i=1}^{N} \color{red} {\pi_i b_i(o_1)\beta_1(i)}\)
前后向算法结合
模型\(\mu\),观察序列\(O=\{o_1, o_2, \cdots, o_t, o_{t+1}\cdots, o_T\}\),\(t\)时刻状态为\(q_t=s_i\)的概率如下 \[ \color {blue} {P(O, q_t = s_i \mid \mu)} = \color{red} {\alpha_t(i) \times \beta_t(i)} \] 推导过程如下 \[ \begin{align*} P(O, q_t = s_i \mid \mu) &= P(o_1\cdots o_T, q_t=s_i \mid \mu) =P(o_1 \cdots o_t, q_t=s_i, o_{t+1} \cdots o_T \mid \mu) \\ &= P(o_1 \cdots o_t, q_t=s_i \mid \mu) \times P(o_{t+1} \cdots o_T \mid o_1 \cdots o_t, q_t=s_i, \mu) \\ &= \alpha_t(i) \times P((o_{t+1} \cdots o_T \mid q_t=s_i, \mu) \quad (显然o_1 \cdots o_t是显然成立的,概率为1,条件忽略)\\ &= \alpha_t(i) \times \beta_t(i) \end{align*} \] 所以,把\(q_t\)等于所有\(s_i\)的概率加起来就可以得到观察概率\(\color{blue} {P(O \mid \mu)}\) \[ \color{blue} {P(O \mid \mu)} = \sum_{i=1}^N\ \color{red} {\alpha_t(i) \times \beta_t(i)}, \quad 1 \leq t \leq T \]
维特比算法
维特比(Viterbi)算法用于求解HMM的第二个问题状态序列问题。即给定观察序列\(O=o_1o_2\cdots o_T\)和模型\(\mu = (A, B, \pi)\),求一个最优的状态序列\(Q=q_1q_2 \cdots q_T\)。
有两种理解最优的思路。
- 使该状态序列中每一个状态都单独地具有最大概率,即\(\gamma_t(i) = P(q_t = s_i \mid O,\mu)\)最大。但可能出现\(a_{q_tq_{t+1}}=0\)的情况
- 另一种是,使整个状态序列概率最大,即\(P(Q \mid O, \mu)\)最大。\(\hat{Q} = arg \max \limits_Q P(Q \mid O, \mu)\)
维特比变量 \(\color{blue}{\delta_t(i)}\)是,在\(t\)时刻,\(q_t = s_i\) ,HMM沿着某一条路径到达状态\(s_i\),并输出观察序列\(o_1o_2 \cdots o_t\)的概率。 \[
\color{blue}{\delta_t(i)} = \arg \max \limits_{q_1\cdots q_{t-1}} P(q_1 \cdots q_{t-1}, q_t = s_i, o_1 \cdots o_t \mid \mu)
\] 递推关系 \[
\color{blue}{\delta_{t+1}(i)} = \max \limits_j [\delta_t(j) \cdot a_{ji}] \cdot b_i(o_{t+1})
\] 路径记忆变量 \(\color{blue}{\psi_t(i) = k}\) 表示\(q_t = s_i, q_{t-1} = s_k\),即表示在该路径上状态\(q_t=s_i\)的前一个状态\(q_{t-1} = s_k\)。
维特比算法步骤
初始化
\(\delta_1(i) = \pi_ib_i(o_1), \; 1 \le i \le N\),路径变量\(\psi_1(i) = 0\)
归纳计算
维特比变量 \(\delta_t(j) = \max \limits_{1 \le i \le N} [\delta_{t-1}(i) \cdot a_{ij}] \cdot b_j(o_t), \quad 2 \le t \le T; 1 \le j \le N\)
记忆路径(记住参数\(i\)就行) \(\psi_t(j) = \arg \max \limits_{1 \le i \le N} [\delta_{t-1}(i) \cdot a_{ij}] \cdot b_j(o_t), \quad 2 \le t \le T; 1 \le j \le N\)
终结
\[ \hat{Q_T} = \arg \max \limits_{1 \le i \le N} [\delta_T(i)], \quad \hat P(\hat{Q_T}) = \max \limits_{1 \le i \le N} [\delta_T(i)] \] 路径(状态序列)回溯
\(\hat{q_t} = \psi_{t+1}(\hat{q}_{t+1}), \quad t = T-1, T-2, \cdots, 1\)
Baum-Welch算法
Baum-Welch算法用于解决HMM的第3个问题,参数估计问题,给定一个观察序列\(O= o_1 o_2 \cdots o_T\),去调节模型\(\mu = (A, B, \pi)\)的参数使得\(P(O\mid \mu)\)最大化,即\(\mathop{argmax} \limits_{\mu} P(O_{training} \mid \mu)\)。模型参数主要是\(a_{ij}, b_j(k) \text{和}\pi_i\),详细信息见上文。
有完整语料库
如果我们知道观察序列\(\color{blue}{O= o_1 o_2 \cdots o_T}\)和状态序列\(\color{blue}{Q = q_1 q_2 \cdots q_T}\),那么我们可以根据最大似然估计去计算HMM的参数。
设\(\delta(x, y)\)是克罗耐克函数,当\(x==y\)时为1,否则为0。计算步骤如下 \[ \begin{align*} & 初始概率\quad \color{blue}{\bar\pi_i} = \delta(q_1, s_1) \\ & 转移概率\quad \color{blue}{\bar {a}_{ij}} = \frac{s_i \to s_j的次数}{s_i \to all的次数} = \frac {\sum_{t=1}^{T-1} \delta(q_t, s_i) \times \delta(q_{t+1}, s_j)} { \sum_{t=1}^{T-1}\delta(q_t, s_i)} \\ & 发射概率 \quad \color{blue}{\bar{b}_j(k)} = \frac{s_j \to v_k 的次数}{Q到达q_j的次数} = \frac {\sum_{t=1}^T\delta(q_t, s_i) \times \delta(o_t, v_k)}{ \sum_{t=1}^{T}\delta(q_t, s_j)} \end{align*} \] 但是一般情况下是不知道隐藏状态序列\(Q\)的,还好我们可以使用期望最大算法去进行含有隐变量的参数估计。主要思路如下。
我们可以给定初始值模型\(\mu_0\),然后通过EM算法去估计隐变量\(Q\)的期望来代替实际出现的次数,再通过上式去进行计算新的参数得到新的模型\(\mu_1\),再如此迭代直到参数收敛。
这种迭代爬山算法可以局部地使\(P(O \mid \mu)\)最大化,BW算法就是具体实现这种EM算法。
Baum-Welch算法
给定HMM的参数\(\mu\)和观察序列\(O= o_1 o_2 \cdots o_T\)。
定义t时刻状态为\(s_i\)和t+1时刻状态为\(s_j\)的概率是\(\color{blue}{\xi_t(i, j)} = P(q_t =s_i, q_{t+1}=s_j \mid O, \mu)\) \[ \begin{align} \color{blue}{\xi_t(i, j)} &= \frac{P(q_t =s_i, q_{t+1}=s_j, O \mid \mu)}{P(O \mid \mu)} = \color{red}{\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{P(O \mid \mu)}} = \frac{\overbrace{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}^{o_1\cdots o_t, \; o_{t+1}, \; o_{t+2}\cdots o_T}} {\underbrace{\sum_{i=1}^N \sum_{j=1}^N \alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}_{\xi_t(i, j)对ij求和,只留下P(O\mid \mu)}} \\ \end{align} \] 定义\(t\)时刻状态为\(s_i\)的概率是\(\color{blue}{\gamma_t(i)} = P(q_t = s_i \mid O, \mu)\) \[ \color{blue}{\gamma_t(i)} = \color{red}{\sum_{j=1}^N \xi_t(i, j)} \] 那么有算法步骤如下(也称作前向后向算法)
1初始化
随机地给参数\(\color{blue}{a_{ij}, b_j(k), \pi_i}\)赋值,当然要满足一些基本条件,各个概率和为1。得到模型\(\mu_0\),令\(i=0\),执行下面步骤
2EM步骤
2.1E步骤 使用模型\(\mu_i\)计算\(\color{blue}{\xi_t(i, j)}和\color{blue}{\gamma_t(i)}\) \[ \color{blue}{\xi_t(i, j)} = \color{red}{\frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum_{i=1}^N \sum_{j=1}^N \alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}} , \; \color{blue}{\gamma_t(i)} = \color{red}{\sum_{j=1}^N \xi_t(i, j)} \] 2.2M步骤 用上面算得的期望去估计参数 \[ \begin{align*} & 初始概率\quad \color{blue}{\bar\pi_i} = P(q_1=s_i \mid O, \mu) = \gamma_1(i) \\ & 转移概率\quad \color{blue}{\bar {a}_{ij}} = \frac{\sum_{t=1}^{T-1}\xi_t(i, j)}{\sum_{t=1}^{T-1} \gamma_t(i)} \\ & 发射概率 \quad \color{blue}{\bar{b}_j(k)} = \frac{\sum_{t=1}^T \gamma_t(j) \times \delta(o_t, v_k)}{\sum_{t=1}^T \gamma_t(j)} \end{align*} \] 3循环计算 令\(i=i+1\),直到参数收敛